Лекция 9. Общие закономерности движения ... Эффективный потенциал. Минимальное и максимальное расстояние до центра поля
реклама

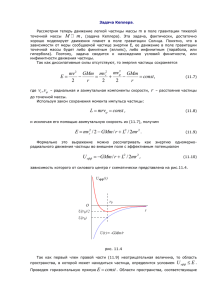
Лекция 9. Общие закономерности движения частицы в кулоновском поле притяжения. Эффективный потенциал. Минимальное и максимальное расстояние до центра поля Рассмотрим движение частицы массы во внешнем поле U r ; r F r U r r 2 r r r (1) когда 0 Это соответствует полю притяжения, y т.е., так называемую задачу Кеплера. Будем считать, что начальный радиус - вектор r0 и начальный импульс p0 P0 P(t) лежат в плоскости XoY . Тогда дви- r(t) r0 жение частицы будет происходить 0 только в этой плоскости Направим ось z так, чтобы она совпадала с направлением t=0 0 O x вектора M 0 [r0 p0 ] . Тогда будем иметь, z что M z M 0 r 0 . Отсюда следует, что 0 и, следовательно, t 0 , где 0 2 - значение азимутального угла при t 0 . Эффективная потенциальная энергия в рассматриваемом поле (1) Uef f M 02 r r 2r 2 (2) Если M 0 0 , то 0 и движение будет происходить по прямой: t 0 . В этом простейшем случае, величина эффективной потенциальной энергии (2) совпадает с реальной потенциальной энергией. Этот случай сводится к одномерному движению, поэтому далее мы будем предполагать, что M 0 0 . В этом случае азимутальный угол t будет монотонно возрастать со временем: t 0 . 1 Исследуем подробно зависимость Uef f r для случая M 0 0 . При r 0 величина Uef f по закону ~ M 02 / r 2 . При r величина Uef f 0 со стороны отрицательных значений по закону ~ / r . В точке M 02 r p , (3) величина Uef f r имеет локальный минимум: Uef f min 2 0, 2p 2M 02 (4) В точке M 02 p r , 2 2 (5) график функции Uef f r обращается в ноль: Другими словами, график зависимости Uef f r , имеет вид «потенциальной ямы». Таким образом, значение величины p определяет как положение точки минимума, так и расстояние, на котором Uef f 0 , т.е. p определяет основные параметры эффективной потенциальной энергии. Поэтому, величину p называют параметром орбиты. В поле притяжения 0 величина p всегда положительна и определяется моментом импульса M 0 . С учетом (5) выражение для величины Uef f r можно записать в виде: Uef f r 1 p 2 r 2r (6) Из формулы (6) видно, что величина p играет роль характерной длины в данной задаче. Поэтому удобно измерять расстояние до центра в единицах p , которое мы будем обозначать буквой (приведенное расстояние): r p r p (7) В терминах приведенных расстояний, формулу (6) можно записать в виде: Uef f 2p 2 1 2 1 2 Uef f min 2 2 (8) Из формулы (8) следует, что U eff имеет минимум при 1 . Из предыдущей лекции нам известно, что область допустимых расстояний до центра поля, где может происходить движение частицы, определяется из уравнения Uef f r E0 . В нашем случае, используя выражение (8), получаем: 1 2 2E0p 2 (9) Решение уравнения (9), квадратного относительно переменной u 1/ , дает: 1,2 1 0 1 e (10) Величина e в формуле (10) определяется выражением: E0M 02 E e 1 2 1 2p 0 2 (11) Величина e p, E0 называется эксцентриситетом орбиты. Параметр орбиты, может быть определен всегда, при заданном значении M 0 . Что касается эксцентриситета орбиты, то величина e p, E0 может быть рассчитана только в том случае, когда выполняется неравенство: 1 2p E0 0, E0 т.е. Uef f 2p min (12) Полная механическая энергия E может быть как положительной, так и отрицательной или равной нулю, в зависимости от начальных значений r0 и v0 : v02 p02 E E0 2 r0 2 r0 (13) Если энергия частицы не отрицательна ( E 0 ), то неравенство (12) выполняется автоматически. В этом случае эксцентриситет орбиты всегда больше или равен единицы: e E0 0 1 2p 3 E 1 (14) Поэтому в формуле (10) можно брать только знак «+», т.к. в противном случае дробь будет отрицательной. Но это означает, что при E 0 уравнение Uef f r E имеет только один положительный корень: r1 E 0 rmin p 1 e (15) Из формулы (15) видно, что при E 0 rmin p / 2 . Т.о., в этом случае имеется только одна точка поворота и движение частицы будет инфинитным в области расстояний от центра поля: rmin r . Теперь рассмотрим противоположный случай, когда энергия частицы отрицательна: E E 0 . В этом случае неравенство (12) будет выполняться не всегда, а только в том случае, если величина энергии частицы удовлетворяет условию E ; 2p M 0 E 0 (16) E (17) В этом случае эксцентриситет орбиты e E 0 1 2p меньше единицы и изменяется в пределах: 0 e E 0 1 Это означает, что при E 0 уравнение Uef f r E имеет два корня: r1 rmin и r2 rmax : rmin E 0 p 1 e и rmax E 0 p 1 e (18) Следовательно, движение частицы финитно, и происходит в области расстояний до центра поля p p r 1 e 1 e (19) Из формулы (19) видно, что эксцентриситет определяет степень “вытянутости” орбиты. Если e 1 то орбита сильно вытянута, т.к. rmin p / 2 , а rmax . Наоборот, если e 0 , то и rmin p и rmax p . Если энергия частицы определяется формулой E0 E 4 2p E (20) r E p E . Следовательно, частица все время находится на одном и то rmin E max том же расстоянии от центра, т.е. вращается по окружности, радиуса p E r0 (21) Здесь r0 - начальное расстояние частицы от центра поля при t 0 . Итак, мы выполнили предварительный анализ характера траектории частицы. Мы выяснили, при каких значениях энергии E0 движение будет инфинитным, финитным и даже определили условия, при которых траектория финитного движения будет окружностью. Мы вычислили скорость вращения по окружности при заданном начальном расстоянии от центра r0 . Теперь проведем анализ возможных траекторий движения в задаче Кеплера. 5