Lekciya10
реклама

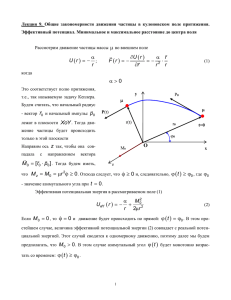
Лекция 10. Движение в кулоновском поле притяжения (задача Кеплера). Классификация орбит при финитном и инфинитном движении В предыдущей лекции мы выяснили, при каких значениях энергии E0 движение будет инфинитным, финитным, а так же определили условия, при которых траектория финитного движения будет окружностью. Мы вычислили скорость вращения при заданном начальном расстоянии от центра r0 . Теперь, проведя общее исследование возможных особенностей движения, получим уравнения траекторий движения частицы в поле притяжения U r / r 0 . Получим уравнения возможных траекторий частицы. Будем использовать полученное ранее выражение для зависимости r , которое фактически уже определяет траекторию движения в неявном виде. Напомним, что r r M0 dr r 2 0 2 E0 U eff r (1) r0 Для определения вида траектории (а не самого закона движения), совершенно не важен выбор знака перед интегралом в формуле (1). Кроме того, в астрономии принято выбирать 0 так, чтобы в начальный момент времени, тело находилось на наименьшем расстоянии от центра, т.е. в перигелии орбиты. С учетом сказанного, выражение (1) для нашей конкретной задачи, можно записать в виде: r r M 0 rmin dr / r 2 M2 2 E 2 02 r r . E / 2 p (2) Используя выражения для параметра и эксцентриситета, введенные в предыдущей лекции, получим: r p rmin dr r 2 p e 2 1 r 2 min 1 d 2 1 e 2 1 2 (3) Здесь, как и ранее, r / p - безразмерное расстояние до центра поля и min 1/ 1 e . Осуществляя в (3) замену переменной интегрирования: x 1/ 1 , dx d / , 2 приводим интеграл к табличному виду: d 1 1 2 e 2 1/ 1 . x arccos arccos e e e x 2 dx 2 2 Поэтому получаем: 1 p 1 p 1 p r arccos 1 arccos 1 arccos 1 . rmin e r e r e rmin r Легко видеть, что второе слагаемое равно нулю. Поэтому: 1 p r arccos 1 e r (4) p 1 e cos (5) Откуда r Это и есть уравнение семейства траекторий в поле притяжения U r / r в полярных координатах. Теперь приступим к анализу выражения (5) для различных значений энергии частицы E0 . Проведем анализ различных траекторий движения в задаче Кеплера, записав уравнение (9.6) r p er cos , в обычных декартовых координатах. Учитывая, что r (6) x 2 y 2 , r cos x запишем x 2 y2 (p ex )2 , т.е. x 2 1 e 2 2 pex y 2 p 2 (7) Это и есть уравнение траекторий в декартовых координатах. Рассмотрим сначала случай финитного движения, когда энергия отрицательна: / 2p E0 0 . В этом случае эксцентриситет орбиты 0 e 1 . Перепишем уравнение (7) в виде 2 x2 2 pe y2 p2 x 1 e2 1 e2 1 e2 (8) Далее 2 pe p 2e2 y2 p2 p 2e2 . x 2 x 2 2 2 1 e2 1 e2 1 e 2 1 e2 1 e p 2 / 1 e2 2 Отсюда видно, что уравнение траектории при финитном движении принимает канонический вид: x x0 2 a2 y2 1 b2 (9) Это есть уравнение эллипса с полуосями a и b с началом координат в точке x 0,0 : a p . 2 1 e 2 E0 b p 1 e2 p 2 E0 M0 2 E0 . x0 ae (10) Поскольку e 1, то a b . Большую полуось эллипса можно было сразу определить из уравнения: 2a rmin rmax . Отсюда получаем, что a 1 p p p 2 2 1 e 1 e 1 e 2 E0 (11) Таким образом, большая полуось эллипса зависит только от энергии частицы. При e 0 получаем уравнение окружности с радиусом p . Таблица 9.1 r 0 rmin p 1 e / 2 p rmax 3 / 2 p p 1 e 2 rmin p 1 e В таблице 9.1 приведены значения нескольких характерных точек траектории при финитном движении, рассчитанные по полученным выше формулам. 3 На рис.1 представлены орбиты движения частицы в поле притяжения U / r 0 при финитном движении для различных значений эксцентриситета 0 e 1 , рассчитанные по формуле (9) в приведенных единицах r / p . Видно, что все орбиты имеют две общие точки 1 при / 2 , когда cos 0 . Рис.1 Орбиты при финитном движении частицы при различных эксцентриситетах орбиты Чтобы вычислить время обращения по эллиптической орбите, т.е. период обращения T воспользуемся законом сохранения момента импульса: M 0 r 2d 2df , где df 1 r r d - площадь сектора орбиты. Интегрируя это равенство по t , получим, что 2 M 0 T 2f , где f - площадь эллиптической орбиты: f ab . Подставляя сюда значения a и b из (9.17), будем иметь: T 2 M0 ab 2 E0 3/ 2 (12) Заметим, что период зависит только от энергии частицы. Теперь рассмотрим случай инфинитного движения, когда энергия положительна: E0 0 . В этом случае эксцентриситет орбиты e 1. 4 Рассмотрим сначала самый простой случай, когда энергия частицы E0 0 , т.е. e 1. В этом случае уравнение (7) принимает вид: y x p p 2x , E0 0 (13) Уравнение (13) есть уравнение параболы в области x p / 2 (красная кривая на рисунке 2. Если E0 0 , т.е. e 1, то уравнение траектории в декартовых координатах будет иметь вид: x x0 a2 2 y2 2 1 b (14) Здесь a p , e 1 2 E0 2 b p e2 1 p 2 E0 M0 , 2 E0 x0 ae (15) Уравнение (15) есть уравнение гиперболы, с «полуосью» a . На рис.2 представлены орбиты движения частицы в поле притяжения U / r 0 при ин- финитном движении для различных значений e 1в эксцентриситета приведенных единицах r/ p. Рис.9.2 Орбиты при инфинитном движении частицы при различных эксцентриситетах орбиты. При E 0 ( e 1) траекториями движения являются гиперболы, огибающие центр поля (фокус) – черная и синяя кривые. При E 0 значение e 1 и траекторией движения является парабола – красная кривая. Видно, что, как и при финитном движении, все орбиты имеют две общие точки 1 при / 2 , когда cos 0 . 5