лабыx

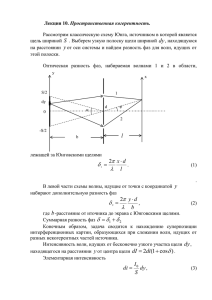
1
1) Монохроматическая волна — строго гармоническая (синусоидальная) волна с
постоянными во времени частотой, амплитудой и начальной фазой.
2) Колебания когерентны, если разность их фаз постоянна во времени и при сложении
колебаний получается колебание той же частоты.
4)
Условия максимумов
Условия минимумов
Разность хода Dd = k·лямбда, где k
= 0, 1, 2...
Разность хода Dd = (2k+1)·лямбда/2
Разность фаз Df = 2·k·pi
Разность фаз Df = (2k+1)·pi
Колебания в точке наложения волн
имеют одинаковую фазу.
Колебания в точке наложения волн имеют
противоположную фазу.
Наблюдается усиление колебаний
Наблюдается ослабление колебаний.
5)

x  xk 1  xk   L .
d
6)
  d   d
x
.
L
7) увеличиваются расстояния между максимумами интерференционной картины;
8) увеличиваются расстояния между максимумами интерференционной картины;
9) к увеличению расстояния между максимумами интерференционной картины
10) Степень приближенности колебаний к идеальной синусоиде
Степень монохроматичности излучения обратно пропорциональна времени когерентности.
11) Временная когерентность волны характеризует сохранение взаимной когерентности при
временном отставании одного из таких лучей по отношению к другому. При этом мерой
временной когерентности служит время когерентности – максимально возможное время
отставания одного луча по отношению к другому, при котором их взаимная когерентность ещё
сохраняется. Временная когерентность определяется степенью монохроматичности.
12) Номер полосы от центра картины (внутри типа)
13) Прошедший через отверстие свет образует расходящийся пучок
14) Радиусом когерентности (или длиной пространственной когерентности) называется
максимальное поперечное направлению распространения волны расстояние, на котором возможно
проявление интерференции. Таким образом, пространственная когерентность определяется
радиусом когерентности. Радиус когерентности
где l — длина волны света, фи — угловой размер источника.
Радиус когерентности — расстояние, при смещении на которое вдоль псевдоволновой
поверхности, случайное изменение фазы достигает значения порядка π.\
2
1) Дифракция (от лат. diffractus — разломанный) волн, явления, наблюдаемые при
прохождении волн мимо края препятствия, связанные с отклонением волн от
прямолинейного распространения при взаимодействии с препятствием. Из-за Д. волны
огибают препятствия, проникая в область геометрической тени.
Принцип Гюйгенса-френеля
Каждый элемент волнового фронта можно рассматривать, как центр вторичного
возмущения, порождающего вторичные сферические волны, а результирующее световое
поле в каждой точке пространства будет определяться интерференцией этих волн.
2)
разделим открытую часть волновой поверхности на кольцевые зоны (зоны Френеля), так
чтобы расстояния от края каждой следующей зоны до точки P отличались друг от друга на
половину длины волны
:
2
r1 = r0 +
;
2
r2 = r1 +

2
= r0 + 2
 ;…;
2
rK = r0 + к
.
2
При таком делении фазы колебаний, приходящих в точку P от соседних зон, отличаются на
т.е. противоположны. Одинаковые площади
3) Амплитуды колебаний зависят лишь от расстояния r и от угла
зоны расстояние rк возрастает, а также растёт угол

,
 . С увеличением номера
 , поэтому амплитуды aк колебаний,
доходящих до точки P от более удаленных зон , должны монотонно убывать по величине с
увеличением номера зоны K:
4) Амплитуду A суммарного колебания в точке P можно представить в виде:
A
a
a
a1 a1
a
a
 (  a2  3 )  ( 3  a4  5 )  ( 5  ... .
2
2
2
2
2
2
Так как слагаемые, выделенные скобками, равны нулю, результирующая амплитуда при
a1 aK
a a
, а при четном K: A  1  K . Объединяя последние

2 2
2 2
a a
получаем A  1  K , где знак “+” относится к нечетному, а знак ““ – к
2 2
нечетном K:
формулы,
A
четному числу зон Френеля, укладывающихся в открытой отверстием части волнового
(5)
фронта. Из сказанного следует, что если отверстие открывает одну зону или их небольшое
нечетное число, то в результате интерференции в точке P будет виден свет, причем более
интенсивный, чем при отсутствии экрана, т.е. образуется дифракционный максимум. При
небольшом четном числе открытых зон освещенность в точке P будет минимальной.
Заметим, что по мере приближения точки P к экрану с отверстием число отрытых для нее
зон будет увеличиваться, так как по мере приближения к экрану увеличивается угол, под
которым видно отверстие в экране. Тогда при соблюдении предложенного Френелем
правила разбиения на зоны, в открытой отверстием части волнового фронта будет
умещаться большее число зон.
5) Уменьшается
6) Сверическая(?)
7)