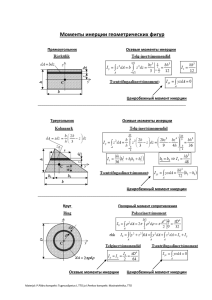
Задача Определить координаты центра тяжести составного сечения, вычислить
реклама

Задача Определить координаты центра тяжести составного сечения, вычислить моменты инерции сечения относительно центральных осей, параллельных сторонам сечения и затем аналитически определить угол наклона главных осей к осям хс0ус, величину главных МИС и главных радиусов инерции, построить эллипс инерции сечения. Исходные данные для решения задачи: - швеллер- Ш №10; - равнобокий уголок- У №8 (80X80X7); - лист- Л 200X10. Рисунок 1 Решение: Найдем положение центра тяжести фигуры по формулам ; . Разобьем фигуру на три простые: швеллер I (берем по ГОСТ 8240-89), прямоугольник II и равнобокий уголок III (берем по ГОСТ 8509-97). Площадь всей фигуры А 0,00109 0, 2*0,01 0,00108 0,00417 м2 Для определения статических моментов выберем вспомогательные оси x`y`, проходящие через верхнюю центральную часть прямоугольника II (рис. 2). Статический момент каждой фигуры равен площади фигуры, умноженной на координату центра тяжести этой фигуры в системе координат x`y`. Суммарные статические моменты Sх 0,00109*(0,05) 0,002*(0,005) 0,00108*0,0223 0,0000404 м2 Sу 0,00109*(0,0856) 0 0,00108*0,084 0,0000571м2 Координаты центра тяжести уцт 0, 0000404 0, 0097 м 9, 7 мм 0, 00417 хцт 0, 0000571 0, 0137 м 13, 7 мм 0, 00417 отложены на рис. 2. Рисунок 2 Проведем через центр тяжести центральные оси х,у (см. рис. 2) и найдем моменты инерции относительно этих осей, как сумму моментов инерций простых фигур, составляющих заданную фигуру. Для определения моментов инерции простых фигур I, II и III используем формулы , , . Моменты инерции относительно собственных осей х0,у0 прямоугольника, уголка и швеллера вычисляем соответственно по формулам и по справочным данным, взятым, из ГОСТ ; , - для прямоугольного листа ; Ix0=174 cм4=174*10-8 м4; Iy0=20,4 cм4=20,4*10-8 м4; Ix0y0=0 – для швеллера Ix0=65,3 cм4=65,3*10-8 м4; Iy0=0; Ix0y0=0 – для уголка Найдем для листа: I x0 I у0 0, 01*0, 23 666, 6*108 м 4 12 0, 2*0, 013 1, 6*108 м 4 12 Отсюда Iх 174 65,3 666,6 10,9*(8,56) 2 0 10,8*8, 4 2 905,9 798,68 762,05 2466,63см4 0,0000247 м4 Iу 20, 4 0 1,6 10,9*(5) 2 20*(0,5) 2 10,8*2, 232 22 272,5 5 53,71 353, 21см4 0,0000035 м4 Ixy=0 Теперь найдем положение главных осей инерции. Угол, на который надо повернуть ось , чтобы она стала главной осью, определяем по формуле : tg 2 2*0 0; 2466, 63 353, 21 2α= 00 α = 00 В соответствие с правилом знаков проводим главные центральные оси инерции Y, Z (см. рис. 3). Вычислим моменты инерции относительно этих осей по формуле : I I 0, 0000247 0, 0000035 (0, 0000247 0, 0000035) 2 02 (0, 0000141 0, 0000106) м4 2 4 max 0, 0000247 м 4 I min 0, 0000035 м 4 Для проверки вычислений удобно использовать следующее свойство: сумма моментов инерций относительно двух любых пар ортогональных осей есть величина постоянная. Тогда должно быть . В нашем примере 0,0000247+0,0000035=0,0000247+0,0000035. Чтобы выяснить, какой момент инерции – максимальный или минимальный соответствует оси X, исследуем знак второй производной функции по формуле = -2*(0,0000247 - 0,0000035)*cos(0)+4*0*sin(0)<0 Отрицательный знак второй производной означает, что оси X соответствует максимальное значение момента инерции, т. е. Iх I max 0, 0000247 м 4 Iу I min 0, 0000035 м 4 Найдем радиусы инерции относительно главных центральных осей по формуле iх и построим эллипс инерции. 0, 0000247 0, 0000035 0, 077 м 77 мм i у 0, 029 м 29 мм 0, 00417 0, 00417 Эллипс инерции показан на рис. 3. Видно, что эллипс вытянут в том направлении, в котором вытянута фигура. Рисунок 3