решением игры по итеративному доминированию.
реклама

Ìîñêîâñêèé ôèçèêî-òåõíè÷åñêèé èíñòèòóò (ÃÓ)
Ôàêóëüòåò èííîâàöèé è âûñîêèõ òåõíîëîãèé
Ìåòîäû îïòèìèçàöèè, âåñíà 2014
Ñåìèíàð 8, ïîèñê ðàâíîâåñèé Íýøà
Áèìàòðè÷íîé èãðîé íàçûâàåòñÿ ïàðà ìàòðèö (A, B) ðàçìåðà m×n. Ïðåäïîëàãàåòñÿ,
÷òî èãðîêè îäíîâðåìåííî è íåçàâèñèìî âûáèðàþò i ∈ {1, . . . , n} è j ∈ {1, . . . , m}, çàòåì
ïåðâûé èãðîê âûèãðûâàåò Aij , à âòîðîé Bij .
Ãîâîðÿò, ÷òî ñòðàòåãèÿ i ñëàáî äîìèíèðóåò ñòðàòåãèþ i0, åñëè ïðè âñåõ j âûïîëíåíî
Aij > Ai j . Åñëè íåðàâåíñòâî ñòðîãîå, òî äîìèíèðîâàíèå íàçûâàåòñÿ ñèëüíûì. Àíàëîãè÷íî îïðåäåëÿåòñÿ äîìèíèðîâàíèå äëÿ ñòðàòåãèé âòîðîãî èãðîêà. Ñòðàòåãèÿ íàçûâàåòñÿ äîìèíèðóþùåé, åñëè îíà äîìèíèðóåò âñå îñòàëüíûå, è äîìèíèðóåìîé, åñëè îíà
äîìèíèðóåòñÿ êàêîé-òî.
ßâëÿåòñÿ ëè îòíîøåíèå äîìèíèðîâàíèÿ ÷àñòè÷íûì ïîðÿäêîì?
Åñëè ó îäíîãî èç èãðîêîâ èìååòñÿ ñèëüíî äîìèíèðóåìàÿ ñòðàòåãèÿ, òî ìîæíî ïðåäïîëîæèòü, ÷òî îí å¼ èñïîëüçîâàòü íå áóäåò. Ïîñëå âû÷¼ðêèâàíèÿ ýòîé ñòðàòåãèè èç îáåèõ
ìàòðèö ó äðóãîãî èãðîêà ìîæåò ïîÿâèòüñÿ äîìèíèðóåìàÿ ñòðàòåãèÿ. Îíà òîæå âû÷¼ðêèâàåòñÿ, è òàê äàëåå. Åñëè â ðåçóëüòàòå îñòà¼òñÿ ðîâíî îäèí èñõîä, òî îí íàçûâàåòñÿ
ðåøåíèåì èãðû ïî èòåðàòèâíîìó äîìèíèðîâàíèþ.
Íàéäèòå ðåøåíèå ïî èòåðàòèâíîìó äîìèíèðîâàíèþ â ñëåäóþùèõ èãðàõ (ïåðâûé
èãðîê âûáèðàåò ñòðîêó, âòîðîé ñòîëáåö, ïåðâîå ÷èñëî â êëåòêå âûèãðûø ïåðâîãî,
âòîðîå âûèãðûø âòîðîãî):
0
1.
2.
a)
b)
U
C
D
U
D
L
2, 3
1, 1
L
3, 3
4, 1
2, 2
R
4, 1
2, 3
M
2, 5
0, 6
1, 3
R
5, 4
2, 7
1, 4
Äâå êóðèöû ïðîäàþò ÿéöà íà ðûíêå, îäíîâðåìåííî è íåçàâèñèìî ïðèíèìàÿ ðåøåíèå, ñêîëüêî ÿèö ïðèíåñòè. Ñíåñòè îäíî ÿéöî ñòîèò 5 ðóáëåé. Åñëè îáùåå êîëè÷åñòâî
ÿèö íà ðûíêå ðàâíî q, òî öåíà óñòàíàâëèâàåòñÿ â ðàçìåðå max{30 − q2, 0}. Êóðèöû
ìàêñèìèçèðóþò ïðèáûëü. Íàéäèòå ðåøåíèå ïî èòåðàòèâíîìó äîìèíèðîâàíèþ.
Ðàâíîâåñèåì Íýøà (÷èñòûì) íàçûâàåòñÿ ïàðà ñòðàòåãèé (i, j), òàêàÿ ÷òî ïðè âñåõ i0
âûïîëíåíî Aij > Ai j , à ïðè âñåõ j 0 âûïîëíåíî Bij > Bij . Òàêèì îáðàçîì, íè îäíîìó
èãðîêó íå âûãîäíî â îäíîñòîðîííåì ïîðÿäêå ìåíÿòü ñòðàòåãèþ.
Äîêàæèòå, ÷òî ðåøåíèå ïî èòåðàòèâíîìó äîìèíèðîâàíèþ ÿâëÿåòñÿ ðàâíîâåñèåì
Íýøà. Äîêàæèòå, ÷òî åñëè èñêëþ÷àþòñÿ òîëüêî ñèëüíî äîìèíèðóåìûå ñòðàòåãèè, òî
ðåøåíèå ïî èòåðàòèâíîìó äîìèíèðîâàíèþ áóäåò åäèíñòâåííûì ðàâíîâåñèåì.
Íàéäèòå âñå ðàâíîâåñèÿ Íýøà â ñëåäóþùåé èãðå. Ïðîêîììåíòèðóéòå.
3.
0
0
4.
5.
U
D
L
1, 0
1, 1
R
0, 0
0, 1
Íàéäèòå âñå ðàâíîâåñèÿ Íýøà â ñëåäóþùåé èãðå. Âåðíî ëè, ÷òî ñëàáî äîìèíèðóåìàÿ ñòðàòåãèÿ ìîæåò èñïîëüçîâàòüñÿ â ðàâíîâåñèè?
6.
U
D
L
0, 0
1, 1
R
0, 0
0, 0
Ñìåøàííûì ðàñøèðåíèåì èãðû (A, B) íàçûâàåòñÿ èãðà, â êîòîðîé èãðîêè âûáèðàþò
ñìåøàííûå ñòðàòåãèè, ò.å. âåðîÿòíîñòíûå ðàñïðåäåëåíèÿ íà ÷èñòûõ ñòðàòåãèÿõ. Åñëè
ïåðâûé èãðîê âûáðàë σ ∈ ∆n, à âòîðîé τ ∈ ∆m, òî âûèãðûø ïåðâîãî èãðîêà ñîñòàâèò
σ T Aτ , à âûèãðûø âòîðîãî σ T Bτ .
Ïîêàæèòå, ÷òî òàê îïðåäåë¼ííûå âûèãðûøè èìåþò ñìûñë ìàòåìàòè÷åñêèõ îæèäàíèé.
Ñìåøàííûì ðàâíîâåñèåì Íýøà íàçûâàåòñÿ ïàðà (σ̂, τ̂ ), òàêàÿ ÷òî ïðè âñåõ σ ∈ ∆n
âåðíî σ̂TAτ̂ > σTAτ̂ è ïðè âñåõ τ ∈ ∆m âåðíî σ̂TB τ̂ > σ̂TBτ .
Íîñèòåëåì ñìåøàííîé ñòðàòåãèè σ íàçûâàåòñÿ ìíîæåñòâî supp σ = {i | σi > 0}.
Äîêàæèòå, ÷òî ïàðà (σ̂, τ̂ ) ÿâëÿåòñÿ ðàâíîâåñèåì òîãäà è òîëüêî òîãäà, êîãäà ïðè
âñåõ i, i0 ∈ supp σ̂ âûïîëíåíî (Aτ̂ )i = (Aτ̂ )i è ïðè âñåõ i ∈ supp σ̂, i0 6∈ supp σ̂ âûïîëíåíî
(Aτ̂ )i > (Aτ̂ )i , à òàêæå àíàëîãè÷íîå óñëîâèå äëÿ âòîðîãî èãðîêà. Èíà÷å ãîâîðÿ, âñå
ñòðàòåãèè, êîòîðûå èãðàþòñÿ ñ ïîëîæèòåëüíîé âåðîÿòíîñòüþ, ïðèíîñÿò îäèíàêîâûé
âûèãðûø, ïðè÷¼ì íå ìåíüøèé, ÷åì òå, êîòîðûå íå èãðàþòñÿ.
Íàéäèòå âñå ÷èñòûå è ñìåøàííûå ðàâíîâåñèÿ â èãðàõ:
7.
8.
0
0
9.
a)
b)
U
D
L
2, 7
4, 2
R
3, 4
1, 5
U
D
L
4, 2
6, 5
R
3, 4
0, 3
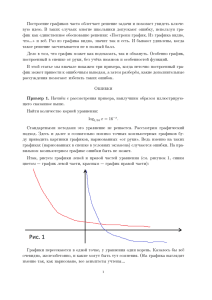
Åñëè ó ïåðâîãî èãðîêà âñåãî 2 ñòðàòåãèè, òî èñêàòü ðàâíîâåñèÿ óäîáíî íà ãðàôèêåñòàêàíå . Ïî ãîðèçîíòàëüíîé îñè îòêëàäûâàåòñÿ ñòðàòåãèÿ ïåðâîãî èãðîêà (îíà çàäà¼òñÿ òî÷êîé èç îòðåçêà [0, 1]), ïî âåðòèêàëüíîé âûèãðûø âòîðîãî èãðîêà. Äàëåå äëÿ
êàæäîé ñòðàòåãèè âòîðîãî èãðîêà ðèñóåòñÿ ãðàôèê âûèãðûøà îò ýòîé ñòðàòåãèè (ýòî
ïðÿìàÿ ëèíèÿ). Ó ïîëó÷åííîé êàðòèíû áåð¼òñÿ âåðõíÿÿ îãèáàþùàÿ (ýòî ëîìàíàÿ). Òî÷êè èçëîìà ýòîé ëîìàíîé (âêëþ÷àÿ êðàÿ) ïðåòåíäåíòû íà ðàâíîâåñèÿ. Ïðè ýòîì åñëè
â òî÷êå èçëîìà ïåðåñåêëèñü ãðàôèêè, ñîîòâåòñòâóþùèå ñòðàòåãèÿì j1 è j2, òî íóæíî
èñêàòü ðàâíîâåñèå ñ íîñèòåëÿìè {j1, j2} ó âòîðîãî èãðîêà è {1, 2} ó ïåðâîãî. Â êðàéíèõ
òî÷êàõ âîçìîæíû ÷èñòûå ðàâíîâåñèÿ.
Íàéäèòå âñå ÷èñòûå è ñìåøàííûå ðàâíîâåñèÿ â ñëåäóþùèõ èãðàõ:
10.
a)
b)
c)
U
D
L
1, 4
2, 3
M
6, 5
5, 1
R
5, 0
7, 4
U
D
L
3, 3
2, 5
M
6, 4
5, 4
R
5, 6
7, 3
U
D
L
1, 4
2, 3
M
6, 3
5, 4
R
5, 0
7, 5