Задача №1
реклама
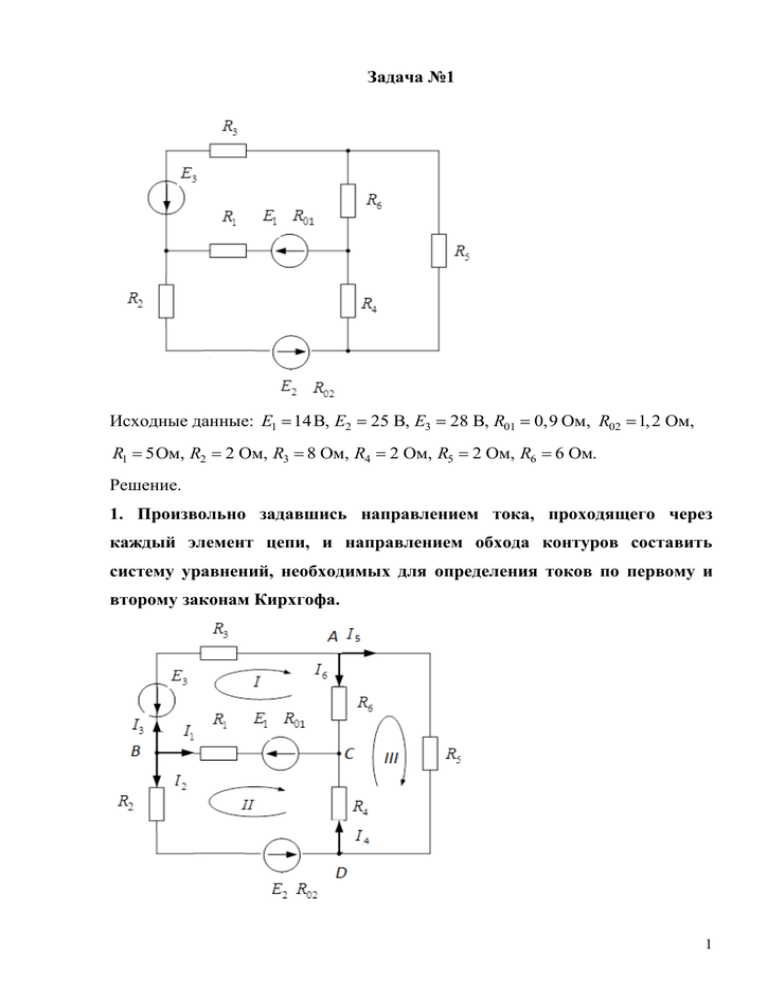
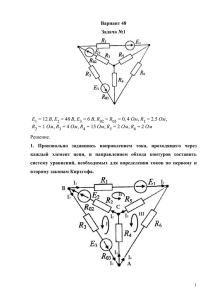
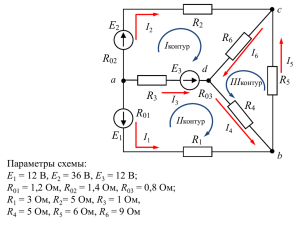
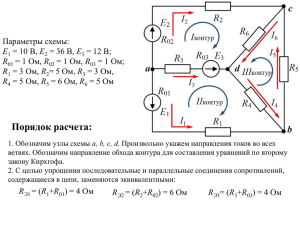
Задача №1 Исходные данные: E1 14B, E2 25 B, E3 28 B, R01 0,9 Ом, R02 1,2 Ом, R1 5Ом, R2 2 Ом, R3 8 Ом, R4 2 Ом, R5 2 Ом, R6 6 Ом. Решение. 1. Произвольно задавшись направлением тока, проходящего через каждый элемент цепи, и направлением обхода контуров составить систему уравнений, необходимых для определения токов по первому и второму законам Кирхгофа. 1 Необходимо определить шесть токов. Цепь содержит четыре узла, по первому закону Кирхгофа составляем три уравнения (на одно меньше числа узлов). Остальные три уравнения составим по второму закону Кирхгофа. Составим уравнения по первому закону Кирхгофа: узел A узел B узел C I 3 I 5 I 6 0, I1 I 2 I 3 0, I 6 I1 I 4 0. Уравнения по второму закону Кирхгофа: I 3 R3 I 6 R6 I1 R1 R01 E1 E3 , контур I I 2 R2 R02 I1 R1 R01 I 4 R4 E1 E2 , I 6 R6 I 5 R5 I 4 R4 0. контур II контур III 2. Преобразовать исходную трехконтурную схему в двухконтурную, заменив «треугольник» сопротивлений эквивалентной «звездой». R45 R4 R5 22 0,4 Ом, R4 R5 R6 2 2 6 R46 R4 R6 26 1,2 Ом, R4 R5 R6 2 2 6 R56 R5 R6 26 1,2 Ом. R4 R5 R6 2 2 6 2 3. Для двухконтурной схемы составить систему уравнений для расчета токов, используя законы Кирхгофа. Рассчитать эти токи. узел B I 3 R3 R56 I1 R1 R01 R46 E1 E3 , контур I I1 R1 R01 R46 I 2 R2 R02 R45 E1 E2 . контур II I1 I 2 I 3 0, Подставим численные значения величин I1 I 2 I 3 0, I 3 8 1,2 I1 5 0,9 1,2 14 28, I1 5 0,9 1,2 I 2 2 1,2 0,4 14 25. I1 I 2 I 3 0, 9,2 I 3 7,1I1 14, 7,1I 3,6 I 39. 1 2 Решив систему уравнений, получим значения токов I1 2,49 A, I 2 5,93 A, I 3 3,44 A. 4. Используя данные значения токов, рассчитать все токи, проходящие через каждый элемент цепи в трехконтурной схеме. По второму закону Кирхгофа для контура I I3 R3 I 6 R6 I1 R1 R01 E1 E3 , контур I откуда I6 E1 E3 I1 R1 R01 I 3 R3 R6 14 28 2,49 5 0,9 3,44 8 5 A, 6 по первому закону Кирхгофа для узла A I 5 I 3 I 6 3,44 0,2 3,42A , по первому закону Кирхгофа для узла C I 4 I1 I 6 2,49 0,2 2,51 A . 5. Изобразить исходную трехконтурную схему и, задав направления контурных токов, составить уравнения по методу контурных токов. 3 По методу контурных токов необходимо составить 3 уравнения, как и по второму закону Кирхгофа. Выберем и обозначим направления контурных токов I k1 , I k 2 , I k 3 . Составим уравнения относительно неизвестных контурных токов: I k1 R3 R6 R1 R01 I k 2 R1 R01 I k 3 R6 E1 E3 I k1 R1 R01 I k 2 R2 R02 R1 R01 R4 I k 3 R4 E1 E2 I k1R6 I k 2 R4 I k 3 R4 R5 R6 0 После подстановки численных значений параметров цепи, получим I k1 8 6 5 0,9 I k 2 5 0,9 I k 3 6 14 28 I k1 5 0,9 I k 2 2 1,2 5 0,9 2 I k 3 2 14 25 I k1 6 I k 2 2 I k 3 2 2 6 0 19.9 I k1 5,9 I k 2 6 I k 3 14 5,9 I k1 11,1I k 2 2 I k 3 39 6 I 2 I 10 I 0 k2 k3 k1 Решим полученную систему уравнений, значения контурных токов: I k1 3,44 A, I k 2 5,93 A, I k 3 3,42 A. 4 6. Определим токи, проходящие через каждый элемент цепи, используя контурные токи. I1 I k 2 I k1 5.93 (3,44) 2.49 A, I 2 I k 5,93 A, I 3 I k1 3,44 A, I 4 I k 3 I k 2 3,42 (5,93) 2,51 A, I 5 I k 3 3,42A, I 6 I k1 I k 3 3,44 (3,42) 0,2A. 7. Составить баланс мощностей для заданной схемы. Уравнение баланса мощностей отражает равенство мощностей, отдаваемой источниками и расходуемой потребителями. Мощность источников. Pист E1I1 E2 I 2 E3 I 3 14 2,49 25 5,93 28 3,44 279,43 Вт . Мощность потребителей. Pпотр I12 ( R1 R01 ) I 22 R2 R02 I 32 R3 I 42 R4 I 52 R I 62 R6 2,492 5 0,9 5,932 2 1,2 3,442 8 2,512 2 3,422 2 0,2 2 6 280,1 Вт. Относительная погрешность расчета составляет P Pист Pпотр Pист 100% 279,43 280,01 100% 0,2% . 279,43 8. Построить в масштабе потенциальную диаграмму для внешнего контура, определив отдельно потенциалы всех промежуточных точек между элементами контура. Построим потенциальную диаграмму для следующего контура: 5 Примем потенциал точки D равным нулю, D 0 , и найдем потенциалы остальных точек контура. G D E2 I 2 R02 25 5,93 1,2 17,884 B, B G I 2 R2 17,884 5,93 2 6,024 B, F B E3 6,024 28 34,024 B, A F I 3 R3 34,024 B-(-3.44) 8 6,504B, D A I 5 R5 6,504 (3.42) 2 0. Построим потенциальную диаграмму 6 7