R E Параметры схемы:
реклама

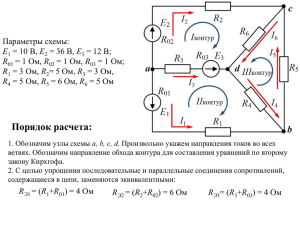
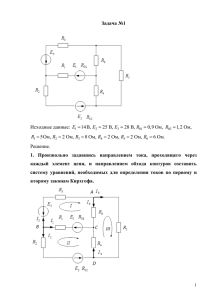
c E2 R2 I2 R6 Iконтур R02 E3 I6 d a IIIконтур R3 I3 R01 E1 I1 Параметры схемы: E1 = 12 В, E2 = 36 В, E3 = 12 В; R01 = 1,2 Ом, R02 = 1,4 Ом, R03 = 0,8 Ом; R1 = 3 Ом, R2= 5 Ом, R3 = 1 Ом, R4 = 5 Ом, R5 = 6 Ом, R6 = 9 Ом I5 R5 R03 R4 IIконтур I4 R1 b Порядок расчета: 1. Обозначим узлы схемы a, b, c, d. Произвольно укажем направления токов во всех ветвях. Если принятое направление тока не совпадает с действительным, в результате расчета такой ток оказывается отрицательным. 2. С целью упрощения последовательные и параллельные соединения сопротивлений, содержащиеся в цепи, заменяются эквивалентными: R1Э = (R1+R01) = 4,2 R2Э = (R2+R02) = 6,4 R3Э = (R3+R03) = 1,8 3. Составляются уравнения по первому закону Кирхгофа, количество которых равно (n–1), где n – количество узлов в схеме, знак тока зависит от ориентации тока, относительно узла: Согласно первому закону Кирхгофа для цепей a : I1 I 2 I3 0; постоянного тока алгебраическая сумма токов в любом узле электрической цепи равна нулю: b : I1 I 4 I5 0; c : I 2 I 5 I 6 0. n Ik 0 k 1 4. Остальные уравнения для независимых контуров составляются по второму закону Кирхгофа. При этом направления обхода контуров выбираются произвольно, знак слагаемых зависит от совпадения или не совпадения с принятым направлением обхода контура. Согласно второму закону Кирхгофа для цепей постоянного тока в любом замкнутом контуре алгебраическая сумма напряжений на резистивных элементах равна алгебраической сумме ЭДС, действующих в данном контуре: m n k 1 k 1 Iк : I 2 RЭ 2 I 6 R6 I3 RЭ3 E2 E3 ; IIк : I3 RЭ3 I 4 R4 I1RЭ1 E3 E1; IIIк : I 4 R4 I5 R5 I 6 R6 0. I k Rk E k 5. Решая полученные системы уравнений совместно, определим значения токов в ветвях (задача решается в MS Excel методом обратной матрицы). Запишем матрицу коэффициентов при неизвестных токах и матрицу-столбец правой части уравнений. Матрица-столбец правой Матрица коэффициентов левой части системы: части системы: •I1 •I2 •I3 •I4 •I5 •I6 -1 1 0 0 -4,2 0 -1 0 1 6,4 0 0 -1 0 0 -1,8 1,8 0 0 1 0 0 5 5 0 -1 1 0 0 6 0 0 -1 9 0 9 = 0 0 0 24 0 0 Значения токов: I1 = -0,869 I2 = 2,093 I3 = -1,224 I4 = -0,290 I5 = -1,159 I6 = 0,934 6. Разворачиваем на схеме отрицательные токи. E2 7. Проведем замену треугольника сопротивлений R4, R5, R6 на эквивалентную звезду Rсо, Rdo, Rbo. R02 a R3 R03 d R01 E1 E3 I6 E3 Rco Rdo o d I3 R03 R4 R01 E1 I5 R5 R3 Iконтур R6 a R2 I2 R2 I2 R02 с E2 c I1 R1 I4 b I3 IIконтур I1 R1 Rbo b 8. Для преобразованной схемы рассчитаем значения эквивалентных сопротивлений. Rсo R5 R6 R4 R6 R4 R5 2,7; Rdo 2,25; Rbo 1,5 R4 R5 R6 R4 R5 R6 R4 R5 R6 9. Составляем по законам Кирхгофа уравнения для расчета токов. o : I1 I 2 I3 0; Iк. : I 2 ( RЭ 2 Rco ) I 3 ( RЭ3 Rdo ) E2 E3 ; IIк. : I1 ( RЭ1 Rbo ) I3 ( RЭ3 Rdo ) E3 E1. 10. Определим значения токов в ветвях (в MS Excel). Матрица коэффициентов левой Матрица-столбец части системы: правой части системы: •I1 •I2 •I3 -1 0 5,7 1 9,1 0 -1 4,05 -4,05 = Значения токов: I1 = 0,87 I2 = 2,09 I3 = 1,22 0 24 0 11. Составляем баланс мощностей цепи. Сумма мощностей всех источников энергии равна сумме мощностей всех приемников. P P Для исходной схемы баланс мощностей имеет вид: И П E1 I1 E2 I 2 E3 I 3 I12 ( R1 R01 ) I 22 ( R2 R02 ) I 32 ( R3 R03 ) I 42 R4 I 52 R5 I 62 R6 . 50,16 50,09 12. Рассчитаем потенциалы точек внешнего контура цепи. Разделим дополнительными точками элементы в ветвях. Примем потенциал точки a равным 0. k с E2 R2 I2 R02 R5 a a 0 k a ( E2 I 2 R02 ) 36 2,09 1,4 33,07 с k I 2 R2 33,07 2,09 5 22,62 R01 I5 I1 E1 R1 m b c I 5 R5 22,62 1,16 6 15,66 m b I1 R1 15,66 0,87 3 13,05 b a m ( E2 I1 R01 ) 13,05 (12 0,87 1,2) 0,006 φ, В φk 33 φc φb 0 φm φa R02 R2 R5 R1 R01 Потенциальная диаграмма внешнего контура цепи R, Ом