Углы и расстояния в пространстве

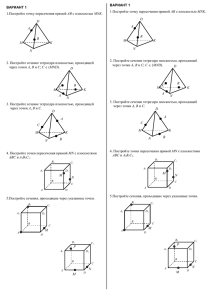
Углы и рас​сто​я​ния в пространстве
Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите
ответ без пробелов, запятых и других дополнительных символов.
1
На ребре A1D1 единичного куба ABCDA1B1C1D1 взята точка К, А1К : KD1 =1 : 2.
а) Постройте сечение куба, проходящее через точку К и параллельное прямым C1D и B1D1.
б) Найдите площадь этого сечения.
2
На ребре AD единичного куба ABCDA1B1C1D1 взята точка К, АК : AD = 1 : 2.
а) Постройте сечение этого куба плоскостью, проходящей через точку К параллельно прямым C1D и B1D1.
б) Найдите площадь этого сечения.
3
В правильной четырёхугольной пирамиде SABCD с вершиной S расстояние между прямыми BD и AS равно 2.
а) Постройте сечение пирамиды плоскостью, проходящей через точки А и S перпендикулярно прямой BD.
б) Найдите объём данной пирамиды, если её боковое ребро равно 5.
4
Радиус основания конуса с вершиной Р равен 8, а длина его образующей равна 12. На окружности основания
конуса выбраны точки А и В, делящие окружность на две дуги, длины которых относятся как 2 : 4.
а) Найдите площадь сечения конуса плоскостью РАВ.
б) Постройте сечение конуса плоскостью, проходящей через точку Р перпендикулярно основанию конуса и
плоскости АВР.
5
В треугольной пирамиде FABC основанием является правильный треугольник АВС, ребро FB перпендикулярно
плоскости основания, стороны основания равны 6, а ребро FA равно 10. На ребре АС находится точка К, на
ребре АВ — точка N, а на ребре AF — точка L. Известно, что FL = 4 и СК = BN = 2.
а) Постройте сечение пирамиды плоскостью, проходящей через точки К, N и L
б) Найдите площадь этого сечения
6
В правильной треугольной призме АВСА1В1С1 через центр основания треугольника АВС и центры симметрий
боковых граней АА1В1В и BB1С1C проведена плоскость, которая составляет с плоскостью основания 30°.
а) Постройте сечение, образованное этой плоскостью.
б) Найдите площадь этого сечения, если сторона основания равна 6.
7
Около шара описана правильная усечённая четырёхугольная пирамида, у которой площадь одного основания
в 9 раз больше площади другого.
а) Докажите, что боковыми гранями усечённой пирамиды являются трапеции, высоты которых равны
среднему арифметическому сторон оснований.
б) Найдите угол наклона боковой грани к плоскости основания.
8
В правильной треугольной призме ABCA1B1C1 косинус угла между прямыми АС1 и В1С равен 1/25.
а) Постройте сечение призмы плоскостью, проходящей через точки А и С1 параллельно прямой B1C.
б) Найдите площадь поверхности данной призмы, если её высота равна 6.
ID_4535
1/3
neznaika.pro
9
10
Высота усечённого конуса равна √3. Прямоугольный треугольник АВС с углом А, равным 60°, и углом С, равным
90°, расположен так, что вершина А лежит на окружности нижнего основания, а вершины В и С — на
окружности верхнего основания. Найдите АВ, если угол между плоскостью АВС и плоскостью основания
усечённого конуса равен 60°.
В треугольной пирамиде FABC основанием является правильный треугольник АВС, ребро FB перпендикулярно
плоскости основания, стороны основания равны 6, а ребро FA равно 10. На ребре АС находится точка К, на
ребре АВ — точка N, а на ребре AF — точка L. Известно, что FL = 4 и СК = BN = 2.
а) Постройте сечение пирамиды плоскостью, проходящей через точки К, N и L
б) Найдите площадь этого сечения
ID_4535
2/3
neznaika.pro
Ответы
1
2
3
4
48√2
5
0,4√579
6
6
7
8
144 + 32√3
9
4
10
0,4√579
Обо всех неточностях пишите на почту (с указанием темы и формулировки задания): dasha@neznaika.pro
Источник: http://neznaika.pro/test/math/p/502
ID_4535
3/3
neznaika.pro