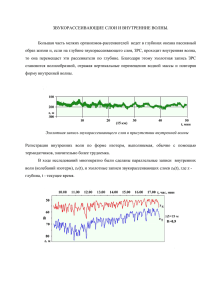
структурная неустойчивость решения задачи распространения
реклама

XXIX Звенигородская конференция по физике плазмы и УТС, 25 февраля – 1 марта 2002 г. СТРУКТУРНАЯ НЕУСТОЙЧИВОСТЬ РЕШЕНИЯ ЗАДАЧИ РАСПРОСТРАНЕНИЯ ВОЛН В НЕОДНОРОДНОЙ ПЛАЗМОПОДОБНОЙ СРЕДЕ И.П. Козлов МАИ (НИИПМЭ), Москва, Россия В докладе теоретически рассматривается взаимодействие электромагнитного излучения с плазмоподобной средой твердого тела вблизи критической концентрации, исследуется структурная неустойчивость решения задачи дифракции по направлению распространения волны. В качестве модельной задачи рассматривается "почти" нормальное падение плоской электромагнитной волны при "сверхмалом" поглощении на "почти" плоскослоистую среду, диэлектрическая проницаемость которой проходит через ноль. Этот случай занимает особое место в теории распространения волн из-за теоретически предсказанного докладчиком явления качественной и количественной зависимости решения исследуемой физической задачи от малых параметров вблизи нуля 1. Выявленная аномалия решения соответствующего волнового уравнения приводит к необходимости учета всех возможных явлений вблизи нуля , соответствующего критической концентрации плазмы. Рассматривается сферически-слоистая среда, образованная вложенными друг в друга однородными диэлектрическими шарами без центральной симметрии, но при осевой симметрии 2. На структурную неустойчивость решения задачи влияют, прежде всего, малые: поглощение (задаваемое Im()), угол падения волны на слой (1) при =1 (или 0=1sin21), обратный радиус (1/r) кривизны поверхности =const, смещение между центрами шаров (ij). Решение устойчиво при значении бифуркационного параметра Im()/01 в этом случае направление распространения волны не меняется. Классическим примером такого случая является решение задачи нормального падения плоской волны на линейный полубесконечный плоский слой диэлектрика без поглощения, полученное в 3 через функции Эйри. Это решение устойчиво при 1, однако при 0 необходимо использовать точное решение соответствующей физической задачи (то есть использовать обе функции Эйри) с учетом малых параметров. Рассмотрено плоскослоистое приближение задачи. Автомодельное решение приводит к сокращению количества независимых параметров слоя. Дан принцип подобия неоднородных слоев, имеющих эквивалентные коэффициенты отражения (при 0). Предложенный метод решения 4-5 предполагает разбиение неоднородного слоя на однородные подслои переменной толщины, согласованной с изменением функции на слое. Полученные количественные критерии применимости коротковолнового и длинноволнового приближений, критерий появления поверхностной волны (при 0.1) и критерий применимости модели нормального падения волны позволяют в плоскослоистом приближении проводить вычисления с заданной точностью, что необходимо из-за выявленной аномалии решения волнового уравнения. Проведенные расчеты вблизи точки бифуркации подтверждают зависимость решения от малых параметров задачи. Уточнены расчеты амплитудных и фазовых характеристик решения задачи для линейного полубесконечного слоя при использовании функций Эйри. Литература [1] Козлов И.П., Письма в ЖТФ, 2000, Т. 26, В.14, С.28 [2] Козлов И.П., Письма в ЖТФ, 2001, Т. 27, В.24 [3] Гинзбург В.Л., Распространение электромагнитных волн в плазме, М:, Наука, 1967 [4] Козлов И.П., Р и Э, 1997, Т.42, №2, С.142 [5] Козлов И.П., ЖТФ, 1999, Т.69, №8, С. 5