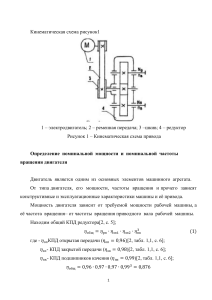
1 КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДА
реклама

1 КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДА 1) Общий КПД привода находим по формуле: об = 1 х 2 х 32 , где 1=0,98 – КПД зубчатой передачи; 2=0,99 – КПД пары подшипников качения; 3=0,93 – КПД цепной передачи; Значит получаем об = 0,98х0,93х0,992 =0,89; Значения КПД механических передач взяты из [1], табл. 1.1., стр. 5 2) Требуемую мощность электродвигателя находим по формуле: Pэдтр Pвых общ 18 20, 22 0,89 Pэд 0,95 Pэдтр Выбираем электродвигатель в соответствии с табличными значениями по ГОСТ 19523-81, см [1], приложения, П1., стр. 390. Выбранная мощность 22кВт (22>20,22). В соответствии с этим выбираем электродвигатель асинхронный серии 4А : 180S4 (S=2,0; Tп/Тн=1,4) nном пс 1 s 1500 1 2 / 100 1470 об/мин 3. Определение передаточных чисел всех передач, входящих в привод. iобщ nном 1470 14, 7 nвых 100 Выбираем для зубчатой передачи стандартное значения по ГОСТ 2185-66 iзуб .перд 4 Следовательно: iцеп iобщ iзуб .пер 14, 7 3, 68 4 2. Tдв -вращающийся момент на валу двигателя Tдв дв Рэд дв пдв 30 3,14 1470 153,9 рад/с 30 20,22 103 Tдв 131,4 Н/м 153,9 Входной вал: Т1 Т дв 131,4 H/м 1 эд 153,9 рад/с п1 пэд 1470 об/мин Р1 Т1 1 131,4 153,9 20,22кВт Выходной вал редуктора: Т 2 Т1 i ред 1 2 131,4 4 0.98 0.99 509.94 H/м 1 2 п2 i ред 153,9 38,48 рад/с 4 п1 1470 367,5 об/мин і ред 4 Р2 Т 2 2 509,94 38,48 19,62кВт 2. РАСЧЕТ ЗУБЧАТОЙ ПЕРЕДАЧИ: Выбор материала для зубчатых колес: Марка стали 40Х Диаметр заготовки, мм Предел прочности, в, МПа Предел текучести, т, МПа Твердость НВ (средняя) До 120 Св. 160 930 830 690 540 270 245 Термообработка Улучшение Допускаемое контактное напряжение определяют при проектировочном расчете по формуле K Н lim b HL SH Здесь H lim b, — предел контактной выносливости при базовом числе циклов (значения H lim b, указаны в табл. 3.2 [1]); Способ термохимической обработки зубьев Нормализация или улучшение Средняя твердость поверхностей зубьев НВ < 350 Сталь Углеродистая и легированная H lim b, МПа 2 НВ + 70 H lim b1=2∙270+70=610МПа H lim b2=2∙245+70=560МПа КHL — коэффициент долговечности; если число циклов нагружения каждого зуба колеса больше базового, то принимают KHL = 1. K HL1,2 6 N HO1,2 N HE1,2 1, но 2,6 при SH = 1,1; NHO - базовое число циклов перемены напряжений N HG1, 2 30 HB12,,24 HB13, 2 120 10 6 N HO1 270 19.7 106 3 N HО 2 245 14.7 106 3 При постоянном режиме нагрузки расчетное число циклов напряжений N HE 1,2 60cn1, 2t , где c - число зацеплений зуба за один оборот (для проектируемого одноступенчатого редуктора с = 1); n1, 2 - частота вращения того зубчатого колеса, по материалу которого определяют допускаемые напряжения, об/мин; t – время работы передачи (ресурс) в часах; t = Lh= 24 Ксут 365 К год L 24 0.2 365 0.5 10 8760 N HЕ1 60 11470 8760 772 106 N HЕ 2 60 1 367,5 8760 193,2 107 Так как N HЕ1,2 N HО1,2 , то принимаем K HL1,2 1. SH - коэффициент безопасности; для колес из нормализованной и улучшенной стали, а также при объемной закалке принимают [SH = 1,11,2; Н 1 610 1 554,5 МПа 1,1 560 1 509,1 МПа 1,1 Для не прямозубых колес расчетное допускаемое контактное напряжение Н 2 [н] = 0,45 ([Н1] + Н2])=0,45(554,5+509,1)=478,62 после определения этих величин следует проверить выполнение условия: Н] 1,23 Н min=1,23*509,1=626,1МПа Условие выполнено 3. РАСЧЕТ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ КОЛЕС НА ВЫНОСЛИВОСТЬ ПРИ ИЗГИБЕ Расчет зубьев на изгибную выносливость выполняют отдельно для зубьев шестерни и колеса, для которых вычисляют допускаемые напряжения изгиба по формуле [1] F 1, 2 F lim1,2 S F 1,2 К FL1,2 , где F lim1,2 - предел выносливости зубьев по напряжениям изгиба, значения которого приведены в табл; Значения предела выносливости при отнулевом цикле изгиба оF lim b и коэффициент а безопасности SF Марка стали 40Х, Твердость зубьев На В Термическая или термохимическая поверхности сердцевине обработка оF lim b, МПа SF Нормализация, улучшение 1,8 НВ 1,75 НВ 180-350 F lim1 F 0 = 1,8*270 = 486МПа F lim 2 F 0 = 1,8*245= 441МПа SF - коэффициент безопасности, рекомендуют (смотри табл.); SF =1,75 KFL - коэффициент долговечности, методика расчета которого аналогична расчету (смотри выше). К FL1,2 6 К FL1,2 6 N FO 1 , N FE1,2 N FG 1 , но 2,6 . N FE1,2 Рекомендуют принимать для всех сталей N FG 4 10 6 . При постоянном режиме нагружения передачи N FE1,2 60 c n1,2 t . N FЕ1 60 11470 8760 772 106 N FЕ 2 60 1 367,5 8760 193,2 107 Так как N FE1,2 N FG то принимаем YN1,2 =1. F 1 486 1 278 МПа 1.75 F 2 441 1 255 МПа 1.75 4. РАСЧЕТ МЕЖОСЕВОГО РАССТОЯНИЯ: a w K a (u 1) 3 T 2K H β [σ H ]2 u 2 ψ ba Для косозубых и шевронных передач Ка = 43,0. КН — коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца. При проектировании закрытых зубчатых передач редукторного типа принимают значения KH = 1,1по табл. 3.1. При проектировании редукторов обычно задаются величиной ba = b / a; для шевронных ba = 0,51,0 принимаем 0,8 509.94 1.1 aW 43 4 1 3 123,88 мм 478.622 42 0,8 Принимаем по ГОСТ2185-66 aW =125мм 5. Модуль зацепления mn (0,01 0,02)a w 1,25 2,5 Принимаем по ГОСТ9563-60 mn 2 мм 6. Количество зубьев шестерни и колеса, значение угла наклона зубьев z 2a w cosβ mn Угол наклона линии зуба принимают для косозубых для шевронных = 2540о принимаем предварительно 30 z z1 2a w cosβ 2 125 cos30 108 mn 2 z 108 21,6 принимаем 22 i 1 4 1 z2 z1 i 22 4 88 Уточненное значение cosβ cosβ (z1 z2 )mn 22 88 2 0.88 2a w 2 125 28o21' Уточняем передаточное число: i z2 88 4 z1 22 Расхождение с принятым ранее номинальным передаточным отношением не превышает 2,5 % условие выполнено и составляет 0% Проверка межосевого расстояния: aw z1 z2 88 22 mn 2 125 мм 2 cos 2 0.88 Условие выполняется ba 2.5 mn 2.5 2 0.045 Условие выполняется. aw cos 125 0.88 Ширина зубчатого венца: Для колеса b2 ψba a w 0,8 125 100 мм Для шестерни b1 b2 5...10 = 100 + 5 = 105 мм Расчет диаметров шестерни и колеса зубчатой передачи: Шестерни: d1 mn 2 z1 22 50 мм cosβ 0,88 da1 d1 2mn 50 2 2 54мм d f 1 d1 2.5 mn 50 2.5 2 45 мм Колеса: d2 mn 2 z2 88 200 мм cosβ 0,88 da1 d1 2mn 200 2 2 204мм d f 1 d1 2.5 mn 200 2.5 2 195 мм Окружная скорость шестерни: V d1 n1 60 1000 3.14 50 1470 3.85 м/с 60000 Степень точности передачи принимаем по ГОСТ 8 Уточняем коэффициент перегрузки: KH KHβKHaKHV 1,14 1,09 1 1,243 KHβ 1.14 при bd b 100 2 и HB 350 табл.3.5 (1) d1 50 KHa 1,09 при 8ст и скорости до 5м/с KHV 1 Проверка величины расчетного контактного напряжения: 3 270 T 2K H (u 1)3 270 509,94 10 4 1 σH 480,59 МПа aw b 2u 2 125 100 4 3 Перегрузка составляет Н Н 100% 0,411 5% условие выполнено Н Силы, действующие в зацеплении Ft 2T 1 2 131,4 5256 Н d1 0,05 Fr Ft tg20 tg 20 5256 2173.9 H cosβ 0.88 Fa F ttgβ =2836.89 РАСЧЕТ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ КОЛЕС НА ВЫНОСЛИВОСТЬ ПРИ ИЗГИБЕ Формула для проверочного расчета зубьев на выносливость по напряжениям изгиба имеет вид (см. ГОСТ 21354-75) FK t F YF YβKFα σF bmn [σF ] Для зубчатых колес, выполненных без смещения, YF имеет следующие значения : zυ1 z1 =32.3 cos3β YF1=3.75 zυ2 z2 =129 cos3β YF1=3.6 F1 278 74.06 YF 1 3.75 F 2 252 68.8 YF 2 3.6 Коэффициент нагрузки КF = 1.32*1.3= 1.72 представляет собой произведение двух коэффициентов: КF,= 1.32 учитывающего неравномерность распределения нагрузки по длине зуба (коэффициент концентрации нагрузки), и KFv= 1.3 учитывающего динамическое действие нагрузки (коэффициент динамичности). Коэффициент Y введен для компенсации погрешности, возникающей изза применения той же расчетной схемы зуба, что и в случае прямых зубьев. Этот коэффициент определяют по формуле Yβ 1 β =0.8 140 Коэффициент KF учитывает неравномерность распределения нагрузки между зубьями. Для узких зубчатых колес, у которых коэффициент осевого перекрытия b tg 100 tg 28o 21' 8.54 mn 3.14 2 При 1 этот коэффициент определяют по формуле 4 (ε a 1)(n 5) 4εα где - коэффициент торцевого перекрытия; n — степень точности зубчатых колес. При учебном проектировании можно принимать среднее значение = 1,5 и степень точности 8-ю; тогда KF = 0,92; b - ширина венца того зубчатого колеса, зубья которого проверяют на изгиб. KFα σF2 5256 1.72 0.8 0,92 3,6 119 252 условие выполнено 100 2 РАСЧЕТ ВАЛОВ : Диаметр вала по элемент открытой передачи: d1 3 T 1000 3 131,4 1000 37,97 мм 0.2 K 0.2 12 d1 = (0.8...1.2)d1(дв), Так как редуктор присоединяется к электродвигателю через муфту нужно согласовать диаметры валов электродвигателя и редуктора, учитывая выше сказанное принимаем диаметр вала редуктора равным диаметру вала электродвигателя 48 мм. Диаметр вала под подшипник и уплотнение: d4 = d2 = d1 + 2t =48+2*2,5=53мм принимаем 55мм Длина l2 1.5 d2 = 1,5*55 = 82мм Диаметр упорного буртика подшипника d3 = d2 + 3.2r=55+3,2*3=65мм Рис.3.1 б Диаметр вала по элемент открытой передачи: d1 3 T 1000 3 509,94 1000 55,4 мм 0.2 K 0.2 15 Принимаем 55мм Диаметр вала под подшипник: d4 = d2 = d1 + 2t =55+2*5=65мм принимаем 65мм Длина l2 1.5 d2 = 1,25*65 = 80мм Диаметр упорного буртика подшипника, его же применяем как диаметр под колесо: d3 = d2 + 3.2r=65+3,2*3=75мм Диаметр упорного буртика колеса: d5 = d3 + 3f = 75+3*2=81мм