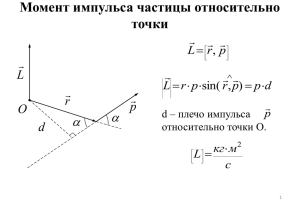
Практическая работа №1 Понятия силы, массы, импульса и энергии в поступательном и вращательном движениях

Введение
Поступательное и вращательное движение
Наиболее простое движение тела — такое, при котором все точки тела
движутся одинаково, описывая одинаковые траектории. Такое движение
называется поступательным. Мы получим этот тип движения, двигая
лучинку так, чтобы она все время оставалась параллельной самой себе.
траектории могут быть как прямыми так и кривыми линиями.
Поступательно движется игла швейной машины, поршень в цилиндре
паровой машины или двигателя внутреннего сгорания, кузов автомашины
(но не колеса!) при езде по прямой дороге и т. д.
Другой простой тип движения — это вращательное движение тела, или
вращение. При вращательном движении все точки тела движутся по
окружностям, центры которых лежат на прямой. Эту прямую называют осью
вращения. Окружности лежат в параллельных плоскостях,
перпендикулярных к оси вращения. Точки тела, лежащие на оси вращения,
остаются неподвижными. Вращение не является поступательным движением:
при вращении оси.
Момент силы
Моментом силы относительно оси вращения называется физическая
величина, равная про­изведению силы на ее плечо.
Момент силы определяют по формуле:
М - FI , где F — сила, I — плечо силы.
Плечом силы называется кратчайшее расстояние от линии действия силы до
оси вращения тела.
Момент силы характеризует вращающее действие силы. Это действие
зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу
надо приложить,
За единицу момента силы в СИ принимается момент силы в 1 Н, плечо
которой равно 1м — ньютон-метр (Н • м).
Правило моментов
Твердое тело, способное вращаться вокруг неподвижной оси, находится в
равновесии, если момент силы М,, вращающей его по часовой стрелке, равен
моменту силы М2, вращающей его против часовой стрелки:
М1 = -М2 или F 1 ll = - F 2 l 2 .
Момент пары сил одинаков относительно любой оси, перпендикулярной к
плоскости пары. Суммарный момент М пары всегда равен произведению
одной из сил F на расстояние I между силами, которое называется плечом
пары, независимо от того, на какие отрезки и /2 разделяет положение оси
плечо пары:
M = Fll + Fl2=F(l1 + l2) = Fl.
Работа момента сил
Работа силы.
Работа постоянной силы, действующей на прямолинейно движущееся тело
, где
— перемещение тела,
— сила, действующая
на тело.
В общем случае, работа переменной силы, действующей на тело,
движущееся по криволинейной траектории
измеряется в Джоулях [Дж].
. Работа
Работа момента сил, действующего на тело, вращающееся вокруг
неподвижной оси
, где
— момент силы, — угол поворота.
В общем случае
.
Совершенная над телом работа переходит в его кинетическую энергию.
Силовые факторы поступательного и
вращательного движения
Закон Галилея — Ньютона гласит: «Всякому действию соответствует равное
и противоположно направленное противодействие». Сказанное поясняется
примерами (рис. 2.9). Тело давит на плоскость силой тяжести Р= mg, а
плоскость оказывает противодействие этому давлению^ Это
противодействие называется реакцией. Сила реакции — R = -Р или Р + R = 0.
В подвешенной нити также возникает реакция, равная силе натяжения нити.
Число реакций равно числу опор. Например, в балке на двух опорах (см. рис.
2.9, б) — две реакции, сумма которых равна силе Р. В общем случае
направление реакций зависит от типа опор и координатных направлений
внешних сил. При контакте сферических тел реакции перпендикулярны
касательным (К—К) и называются нормальными реакциями — Л'(см. рис.
2.9, г, д). Так как любая сила может быть представлена суммой нескольких
сил
Рис. 2.9. Действие сил при вращательном и поступательном движениях ких
сил, то для удобства расчетов в плоской системе суммарные реакции
разлагаются на две слагаемые, направленные по осям координат, т.е. (см. рис.
2.9, б, в)
Тогда для балки (ем. рис. 2.9, в) имеем четыре неизвестные реакции, но с
известными направлениями. Если сумма реакций не равна действующей
активной силе (или сумме внешних сил), тело должно двигаться — это
неравновесная система, подчиняющаяся уравнениям динамики.
Рис. 2.10. Пара сил и момент силы
Силовой фактор вращательного движения. Любые две равные параллельные
и противоположно направленные силы Р образуют так называемую пару сил
(рис. 2.10). Если эти силы не действуют по одной прямой, то их нельзя
заменить одной силой, действие которой было бы равнозначно этим двум
параллельным силам (хотя сумма проекций этих сил на оси координат равна
нулю). Пара сил стремится создать вращение тела, к которому они
приложены. Количественно пара сил выражается моментом сил М = Ph.
Величина М является самостоятельным силовым фактором вращательного
движения и определяет изменение кинематических параметров (угловой
скорости, углового ускорения) вращения. Сила же Р определяет изменение
кинематических факторов поступательного движения.
Пару сил можно переносить в любую плоскость, параллельную данной, не
изменяя ее действия на тело.
Равнодействующий (главный) момент является простой суммой всех
моментов, действующих в данной плоскости. Например, главные моменты
силовых пар (см. рис. 2.10, б)
Здесь за положительное направление принято вращение против часовой
стрелки.
Рис. 2.11. Опрокидывание стенки
На рис. 2.11 показана стенка, на которую действует опрокидывающая
сила Р. Если реакция R = 0, то стенку нельзя опрокинуть любым силовым
моментом. В данном случае R — это сила трения стенки о поверхность.
Логически это объясняется тем, что любой момент — это пара сил и если
одна из сил, составляющих пару, равна нулю, то и опрокидывающий момент
равен нулю. Реакция равна нулю, когда стенка лежит на плоскости, трение по
которой равно нулю. В самом деле, опрокидывающий момент М = PH, а
момент придающий устойчивость стенке М= mgb. Очевидно для
опрокидывания необходимо условие: mgb < PH. Тогда опрокидывающая
сила Р =
= mgb/H. В то же время, исходя из понятия момента как пары сил величина R
= Р. Минимальная величина опрокидывающего плеча Н = mgb/R. При R = 0
величина плеча равна бесконечности, что доказывает невозможность
опрокидывания (т.е. вращения) при отсутствии сопротивления перемещению
стенки но плоскости. Момент опрокидывания можно создать силой Q на
плече h.
Возьмем конкретный пример. Пусть скольжению стенки препятствует сила
трения F (равная реакция R). Сила F пропорциональна давлению на
поверхность и в данном случае выражается зависимостью F = mgf, где / —
коэффициент трения. В равновесном положении Р = F. Эти силы образуют
пару сил с плечом Я.
Тогда из условия опрокидывания mgb < fmgH, получаем, что плечо
приложения силы Р должно удовлетворять условию: Я > b/f. Примем
толщину стенки В = 2 м, коэффициент трения/= 0,4. Плечо силы тяжести b =
В/2. В этом случае опрокидывающее плечо должно быть не менее 2,5 м.
Чтобы опрокинуть стенку высотой 2 м, необходимо увеличить
сопротивление ее перемещению, например, поставив специальный упор
вблизи точки А.
При вращении силовой фактор, т.е. силовой момент
как
так
Линейная скорость связана с угловой соотношением V = wr.
С учетом этого получим
Для системы точечных тел
Величина /называется геометрическим моментом инерции тела. Таким
образом, на основе уравнения Ньютона (1.2) получаем его аналог,
выражающий уравнение динамики вращательного движения в общей форме
Отметим еще раз, что уравнение Ньютона (1.2) является общей формой
уравнения динамики поступательного движения. В уравнениях (1.2)—(2.14)
силовые факторы М и Р связаны с кинематическими параметрами движения
— со и V. Величина J выступает как аналог массы во вращательном
движении и показывает, что при анализе вращательного движения нужно
знать не только массу тела, но и ее распределение в пространстве по
отношению к оси вращения.
При вращении плоского тела его можно представить в виде множества
материальных точек, так что их общий момент инерции
Здесь Yjmi = т — массе всего тела, гх — радиус (расстояние до оси вращения)
каждой элементарной массы. При приближении элементарных масс к их
бесконечно малым величинам, получаем интегральную форму для
вычисления момента инерции
Приведем примеры вычисления момента инерции некоторых тел. Вычислим
величинуJ для пластин одинаковой массы, но с разными центрами вращения
(рис. 2.12). Выделим узкую полоску с элементарной массой
шириной dr (заштрихована). Величина элементарной массы выразится в виде
Рис. 2.12. Вращение одинаковых пластин с разными центрами вращения
произведения объема полоски на плотность dm = ybdF, где dF— выделенная
площадка толщиной Ь, у — плотность.
Величина dF = 2rtg(a/2)dr = 2rtg(B/2R)dry dm = 2brdrtg(B/2R) = Drdr, D
= const. Подставив dm в формулу (2.17), получим
Вычисление но рис. 2.12 дает значение JB = DR4/12 (в три раза меньше). В
физическом смысле это означает, что пластину в положении «а» привести в
движение до заданной скорости труднее, чем в положении «б». При этом
соотношение силовых моментов для разгона тела до заданной скорости (при
одинаковом времени разгона) будет равно 3:1. Соответственно, работа для
остановки тела «а» будет превышать в 3 раза работу для остановки тела в
положении «б». Сравнение кинематических и силовых параметров от вида
движения приведено в табл. 2.1.
Основные силовые и кинематические параметры
Параметры
Поступательное движение
Вращательное движение
Кинематиче
ские
Сила — Ру Н
Силовой момент — М = Ph, Нм
Силовые
Масса — Шу кг
Динамические характеристики вращательного
движения. Момент силы. Момент импульса
При поступательном движении системы все ее точки проходят одинаковые
пути, имеют в данный момент времени одинаковые скорости и ускорения.
При вращательном движения твердого тела все эти характеристики различны
для разных точек вращающегося тела, поэтому и математическая форма 2-го
закона Ньютона будет иной. При вращательном движении существенно
изменяются сами понятия причины, вызывающей вращение, и величины,
определяющей инертность тела.
При поступательном движении динамическими характеристиками являются
сила, масса, импульс. При вращательном движении динамическими
характеристиками являются момент силы, момент инерции, момент
импульса. Эти характеристики можно рассматривать относительно точки
вращения (полюса) и относительно оси вращения. В дальнейшем будем
рассматривать эти характеристики относительно оси вращения. Определим
эти характеристики.
1. Момент силы, действующей на материальную точку, относительно
оси вращения
а) Пусть материальная точка массы m вращается относительно оси ОО ΄.
Обозначим r - радиус-вектор, проведенный от оси вращения до точки
приложения силы F (Рисунок 10).
Рисунок 10. Вращение материальной точки
Моментом силы F относительно оси вращения называется вектор M,
равный векторному произведению радиус-вектора на вектор силы M = [ r∙
F] и направленный по оси вращения в сторону, определяемую по правилу
правого буравчика Модуль вектора момента силы равен M = F∙r∙sinα, где α угол между векторами rи F.
2. Момент импульса
Моментом импульса материальной точки относительно оси вращения
называется вектор L, равный векторному произведению радиусавектора r на вектор импульса P: L = [ r∙P] = [ r∙ mv], где m, v соответственно масса и вектор скорости точки. Направление Lопределяется
по правилу правого буравчика. Модуль вектора L = mv∙ r∙ sinα, где α - угол
между векторами r и v.
3. Момент инерции материальной точки относительно оси вращения
Моментом инерции материальной точки относительно оси вращения
называется физическая величина, численно равная произведению массы
точки на квадрат расстояния точки до оси вращения (Рисунок 10).
I = mr2
Момент инерции - величина скалярная.
Моментом инерции механической системы относительно неподвижной оси
называется физическая величина, равная сумме произведений масс всех
точек системы на квадраты их расстояний до оси вращения.
I=
mi∙ ri2
Для твердого тела, разбитого на элементарные массы ∆ mi, момент инерции
относительно оси равен I =
∆ mi∙ ri2.
Основное уравнение динамики вращательного
движения
1. При поступательном движении уравнение второго закона Ньютона имеет
вид dP/dt = F.
Для вращательного движения: dL/dt = M.
Это уравнение называется уравнением моментов или основным законом
вращательного движения. Вид уравнения не изменится и для системы
материальных точек и для вращения твердого тела, только L определяется
как момент импульса для системы точек.
2. Еще один вид уравнения второго закона Ньютона для вращательного
движения имеет вид:
M∙ dt = dL,
где величина M∙ dt называется импульс момента сил, а dL - изменение
момента импульса системы.
Момент импульса твёрдого тела
Пусть твёрдое тело вращается вокруг закреплённой оси z с угловой
скоростью . Для нахождения момента импульса тела рассматриваем его
как механическую систему материальных точек. Мысленно разобьём тело на
элементарные части массойmi, которые можно принять за материальные
точки. Очевидно, что момент импульса
тела относительно оси равен
векторной сумме
отдельных элементарных частей тела относительно той
же оси. При вращении тела все его точки движутся по окружностям
различного радиусаRi, плоскости которых перпендикулярны к оси вращения.
Поэтому моменты импульсов
всех элементарных частей тела, согласно
правилу правого винта, направлены в одну сторону вдоль оси вращения.
Тогда векторное сложение заменяется скалярным, т.е.
(9)
Используя формулу (7), имеем:
скорости i-ой части. Но i = Ri. Поэтому
где
⎯ модуль линейной
, и с учётом
выражения (9)
Поскольку все точки тела обладают
одинаковой угловой скоростью, то её выносим за знак
суммы:
Так как
⎯ момент инерции тела,
то Lz = Iz. Запишем это выражение в векторном виде:
(10)
Итак, момент импульса твёрдого тела относительно оси
вращения равен произведению момента инерции тела относительно той
же оси на его угловую скорость. Направление
находят по правилу правого винта.
, как и направление ,
Аналогия между вращательным и поступательным движением
Рассмотрев поступательное и вращательное движения можно установить
аналогию между ними. В кинематике поступательного движения
используются путь s, скоростьи ускорениеа. Их роль во вращательном
движении играют угол поворота, угловая скоростьи угловое ускорение ε.
В динамике поступательного движения применяются понятия силы
массыти импульса
,
Во вращательном движении роль силы играет момент
силы, роль массы — момент инерцииIzи роль импульса — момент
импульса Зная формулы поступательного движения легко записать
формулы вращательного движения. Например, скорость и ускорение тела
при поступательном движении вычисляются по формулам
и
Тогда угловая скорость и угловое ускорении при вращательном движении
находится по формулам
импульс тела равен
импульса равен
и
При поступательном движении
Поэтому при вращательном движении момент
Эту аналогию можно продолжать и дальше.
Основной закон динамики вращательного движения твёрдого тела
Пусть тело с моментом инерции Izвращается относительно осиzпод
действием равнодействующего момента
сил. Запишем второй закон
Ньютона, являющимся основным законом динамики поступательного
движения:
и
Здесь ит— ускорение и масса тела, — импульс
тела и — равнодействующая сил, приложенных к телу. Тогда, пользуясь
аналогией между поступательным и вращательным движениями, получаем
две записи основного закона динамики вращательного движения:
(11)
(12)
+Их формулировка: угловое ускорение, приобретаемое телом,
пропорционально моменту внешних сил, приложенных к нему,
относительно оси вращения, и обратно пропорционально моменту
инерции тела относительно той же оси.
Момент внешних сил, действующих на тело, относительно оси
вращения равен производной по времени от момента импульса тела
относительно той же оси. Соотношение (12) является более общей
записью основного закона динамики вращательного движения тела, так как
оно оказывается справедливым и для тел, у которых момент инерции тела не
является постоянной величиной.
Кинетическая энергия вращающегося тела
Кинетическая энергия – величина аддитивная. Поэтому кинетическая
энергия тела, движущегося произвольным образом, равна сумме
кинетических энергий всех n материальных точек, на которые это тело
можно мысленно разбить:
,
(1.1.1)
Если тело вращается вокруг неподвижной оси z с угловой скоростью
линейная скорость i-й точки
вращения. Следовательно,
,
, то
, Ri – расстояние до оси
(1.1.2)
Сопоставив (1.1.1) и (1.1.2), можно увидеть, что момент инерции
тела I является мерой инертности при вращательном движении, так же как
масса m – мера инерции при поступательном движении.
В общем случае движение твердого тела можно представить в виде суммы
двух движений – поступательного со скоростью vc и вращательного с
угловой скоростью ω вокруг мгновенной оси, проходящей через центр
инерции. Тогда полная кинетическая энергия этого тела
,
(1.1.3)
Здесь Ic – момент инерции относительно мгновенной оси вращения,
проходящей через центр инерции.
Список литературы
1. Техническая механика - Гребников В.З
2. Физика: Универсальный справочник