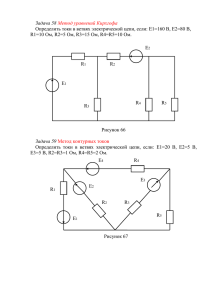
3 Введение При изучении теоретических основ электротехники, теории электрических цепей и электротехники большую роль играет решение задач. В «Методическом пособии по расчету линейных электрических цепей» предложены задачи различной степени сложности, которые могут быть использованы как при проведении практических занятий по указанным выше дисциплинам, так и для самостоятельной работы студентов. Пособие состоит из двух глав и приложения. Все примеры и задачи в сборнике составлены и решены авторами. Задачи составлены таким образом, что объем вычислительных операций в процессе решения сведен к минимуму. Это позволяет сосредоточить основное внимание на методической стороне вопросов. В первой главе рассматривается теория цепей постоянного тока, разбираются различные методы расчета. По каждому методу дается краткая теория, примеры с подробными решениями. Для лучшего усвоения материала примеры располагаются в порядке увеличения трудности. Вторая глава посвящена расчету цепей синусоидального тока символическим методом, включая трехфазные цепи. В приложении дается алгебра комплексных чисел. Пособие специальностей. рекомендуется для электрических и неэлектрических 4 1. Расчет цепей постоянного тока 1.1. Законы Кирхгофа. Энергетический баланс Законы Кирхгофа являются основными законами электрических цепей. Согласно первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю: I 0 (1.1.1) Согласно второму закону Кирхгофа, алгебраическая сумма падений напряжений вдоль замкнутого контура цепи равна алгебраической сумме электродвижущих сил (ЭДС), действующих в этом контуре: I n Rn E (1.1.2) В любой электрической цепи должен соблюдаться энергетический баланс (равенство между суммой мощностей источников энергии, работающих в режиме генератора, и потребляемой мощностью в цепи), т.е.: Pист Pпотр или E I U I I K2 RK (1.1.3) Рассмотрим методику применения законов Кирхгофа и составления энергетического баланса на конкретном примере. 5 Примеры решения задач Пример 1.1 С помощью уравнений, составленных по законам Кирхгофа , найти токи в ветвях схемы при следующих значениях сопротивлений и ЭДС: R1=4 Ом, R2=3 Ом, R3=2 Ом, Е1=4 В, Е2=2 В, Е3=14 В. Составить энергетический баланс. а I1 Е3 I2 R1 R2 Е2 R3 I3 b Е1 Произвольно выбираем направления токов I1, I2, I3. Так как в схеме три ветви, то общее число уравнений, составленных по обоим законам, должно быть равно 3. Составляем одно уравнение по первому закону Кирхгофа (т.к. в схеме два узла), например, для узла «а» (см. рисунок): I1 I2 I3 (а) Если составить еще одно уравнение для узла «b», то оно повторяет уравнение (а): I2 I3 I1 Это доказывает, что по первому закону Кирхгофа необходимо составить число уравнений на единицу меньше числа узлов в схеме. Составим еще два уравнения по второму закону Кирхгофа. Выберем левый и правый контуры. Они являются независимыми, так как каждый из них содержит ветвь, не входящую в другой контур. Направление обхода выбираем по часовой стрелке. Для левого контура: I R I R E E 1 1 2 2 2 1 (б) 6 I3 R3 I2 R2 E3 E2 Для правого контура: (в) Если составить еще уравнение и для внешнего (зависимого) контура, то оно будет линейной комбинацией уравнений (б) и (в), результатом их сложения, не будет нести новой информации и, следовательно, является лишним. Для внешнего контура при обходе по часовой стрелке получим: I1 R1 I 3 R3 E3 E1 (г) Уравнение (г) получается в результате сложения уравнений (а) и (б), т.е. является их линейной комбинацией. Его можно использовать вместо уравнения (б) или (в). Подставив значения сопротивлений и ЭДС в (а), (б), (в) получим окончательно систему уравнений для определения токов: I1 I 2 I 3 0 4 I1 3I 2 2 4 3I 2 I 14 2 2 3 (1' ) (2' ) (3' ) Решим полученную систему методом подстановки (последовательного исключения неизвестных). Из (3'): I 3 12 3I 2 1 2 Из (2'): I1 2 3I 2 1 4 Подставим I1 и I3 в (1'): 1 3 3 I 2 I 2 6 I 2 0 , откуда 2 4 2 I 2 2 A Далее ток: I1: I1 2 3 2 I 3 12 3I 2 1 1 A 4 1 1 12 6 3 A 2 2 Составим энергетический баланс: Pист Pпотр 7 I1 E1 I 2 E2 I 3 E3 I12 R1 I 22 R2 I 32 R3 ; 1 4 2 2 3 14 12 4 22 3 32 2 ; 34=34 В данном случае ЭДС Е1 и Е2 работают как потребители. Примечание. В задачах 1.1.1-1.1.8 для облегчения вычислений дополнительно задаются некоторые значения токов или напряжений. Задачи для самостоятельного решения Задача 1.1.1 U4 E4 R4 I4 а в R3 I3 Е2 I1 R5 Е6 R1 R2 I2 I5 R6 I6 Дано: R1=1 Ом, R2=2 Ом, R3=3 Ом, R4=2 Ом, R5=1 Ом, R6=4 Ом, Е2=11 В, Е4=2 В, Е6=1 В. Требуется определить все токи и составить энергетический баланс, если: а) I3=1 А, I6=1 А (решение приведено в конце параграфа). б) U4=4 В, U6=4 В. в) I2=3 А, I5=1 А. г) U2=6 В, U5=1 В. 8 Задача 1.1.2 Е1 R5 I2 I4 U4 R1 R2 R4 E5 E4 I1 I5 E3 I3 R3 Дано: R1=2 Ом, R2=2 Ом, R3=3 Ом, R4=1 Ом, R5=1 Ом, E1=6 B, Е3=5 В, Е4=1 В, Е5=4 В. Используя уравнения по законам Кирхгофа, определить все токи и составить энергетический баланс, если: а) I1=1 А. б) I2= 2 A. в) U5=2 B. г) U4=1 В. 9 Задача 1.1.3 Дано: R1=2 Ом, R3 R2=1 Ом, I3 R4 I2 R2 R3=1 Ом, R4=3 Ом, R6 R5=2 Ом, R6=1 Ом. E2 I4 E1=1 B, E2 =8 B, E6 I1 R1 E1 E6=2 B. R5 I5 Определить все токи, используя законы Кирхгофа, если: а) I1=1 A, I4=1 A б) U3=2 B, U6=4 B в) I2=3 A, I6=1 A г) U1=2 B, U6=1 B. Составить энергетический баланс. Задача 1.1.4 I3 R3 Дано: R1=3 Ом, R2=2 Ом, E3 R3=1 Ом, R4=1 Ом, Е2 R5=2 Ом, E1=5 B, R2 E4 R1 I2 I1 R5 I4 E4=2 B, E5=5 B. R4 E1 E2=1 B, E3=3 B, I5 Составить уравнения по законам Кирхгофа, E5 определить все токи и составить энергетический баланс, если: а) I1=2 A б) I2=1 A в) U4=1 B г) U5=4 B. 10 Задача 1.1.5 В схеме задачи 1.1.1 известными являются: сопротивления: R3=6 Ом, R4=4 Ом, R5=2 Ом, R6=8 Ом, ЭДС: E2=11 B, E4=2 B, E6=1 B, токи: I1=1 A, I2=1,5 A, I5=0,5 A. Составить уравнения по законам Кирхгофа, найти неизвестные токи ветвей и сопротивления. Задача 1.1.6 В схеме задачи 1.1.2 известными являются сопротивления: R4=2 Ом, R5=2 Ом; R3=6 Ом, ЭДС: E1=6 B, E3=5 B, E4=1 B, E5=4 B; токи: I1=0,5 A, I2=1 A, I5=1 A. Составить уравнения по законам Кирхгофа, найти неизвестные токи ветвей и сопротивления R1 и R2. Задача 1.1.7 В схеме задачи 1.1.3 известными являются сопротивления: R4=6 Ом, R5=4 Ом, R6=2 Ом; R3=2 Ом, ЭДС: E1=1 B, E2=8 B, E6=2 B; токи: I1=0,5 A, I2=1,5 A, I5=1 A. Составить уравнения по законам Кирхгофа, найти неизвестные токи ветвей и сопротивления R1 и R2. Задача 1.1.8 В схеме задачи 1.1.4 известными являются сопротивления: R4=2 Ом, R5=4 Ом; R3=2 Ом, ЭДС: E1=5 B, E2=1 B, E3=3 B, E4=2 B, E5=5 B; токи: I1=1 A, I2=0,5 A, I5=1 A. Составить уравнения по законам Кирхгофа, найти неизвестные токи ветвей и сопротивления R1 и R2. 11 Пример решения задачи 1.1.1 (задача 1.1.1 а)). I3=1 A, I6=1 A. Определить остальные токи. Составим уравнения по законам Кирхгофа: для узлов а) I3 I4 I2 б) I3 I5 I1 г) I1 I6 I2 для контура абга : I3 R3 I1 R1 I2 R2 E2 т.е. 1 3 I1 1 I2 2 11 Итак, рассмотрим три последних уравнения: I1 I5 1 (1) I1 I2 1 (2) I1 2 I2 8 (3) Вычитая из уравнения (3) уравнение (2), получим, 3 I2 9 А, I2 3 A. Далее, из (2) из (1) I1 1 I 2 1 3 2 A I 5 I1 1 2 1 1 A I 4 I 2 I3 3 1 2 A . Энергетический баланс: I2R I2R I2R I2R I2R I2R E I E I E I 1 1 2 2 3 3 4 4 5 5 6 6 2 2 4 4 6 6 2 2 1 32 2 12 3 2 2 2 12 1 12 4 11 3 2 2 1 1 38 Вт =38 Вт (верно).