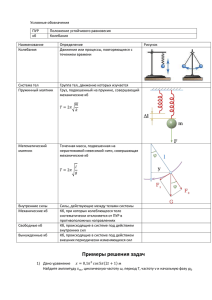
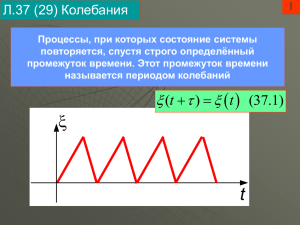
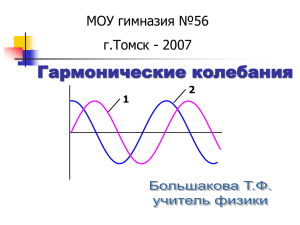
Свод основных определений и соотношений Лекция №1 Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Гармонические колебания – колебания, при которых колеблющаяся величина изменяется с течением времени по закону синуса или косинуса. x(t ) A cos( t ) Уравнение гармонических колебаний: V (t ) x A sin( t ) Скорость: Ускорение: a(t ) x A 2 cos( t ) Свободные колебания без затухания 2-ой закон Ньютона: Fупр =ma Дифференциальное уравнение свободных k 02 x 02 x 0 механических колебаний без затухания: m Вид решения этого ур-ния: x(t ) A cos(0t ) mV 2 mA02 sin 2 (0t ) 2 2 2 2 kx kA Потенциальная энергия: Wp cos2 (0t ) 2 2 m 02 A2 kA2 Wполн Wk Wp Полная механическая энергия: 2 2 Кинетическая энергия: Wk В процессе колебаний происходит взаимопревращение кинетической и потенциальной энергии, так что полная механическая энергия незатухающих колебаний остается постоянной. Дифференциальное уравнение свободных q 02 q 0 электрических колебаний без затухания : q(t ) q0 cos(0t ) Вид решения этого ур-ния: Напряжение на обкладках q(t ) q0 U cos(0t ) C конденсатора: C C Сила тока в цепи колебательного контура: I (t ) q q00 sin(0t ) q2 q2 0 cos2 (0t ) 2C 2C LI 2 Lq0202 Wмагн sin 2 (0t ) 2 2 q02 Lq0202 Wполн Wэл Wмагн const 2C 2 Свободные колебания с затуханием 2-ой закон Ньютона: Fупр +Fсопр =ma Энергия электрических колебаний: Wэл Fсопр =-rV, где r – коэффициент сопротивления β – коэффициент затухания r 2 m Дифференциальное уравнение затухающих колебаний x 2 x 02 x 0 Зависимость амплитуды затухающих колебаний от времени Частота затухающих колебаний 2 2 A(t ) A0e t 0 Общий вид решения диф. ур-ния x(t ) A0e t cos( 02 2 t ) Время, за которое амплитуда колебаний уменьшается в е раз логарифмический декремент затухания 1 t λ=β Т Дифференциальное уравнение затухающих электрических колебаний q 2 q 02 q 0 q(t ) q0e t cos( 02 2 t ) Общий вид решения диф. ур-ния q0e Критическое сопротивление Rкр 2 Добротность колебательного контура R t 2L 1 R2 cos( t ) LC 4 L2 L C Q 1 L R C