Условные обозначения ПУР Положение устойчивого равновесия кб
реклама
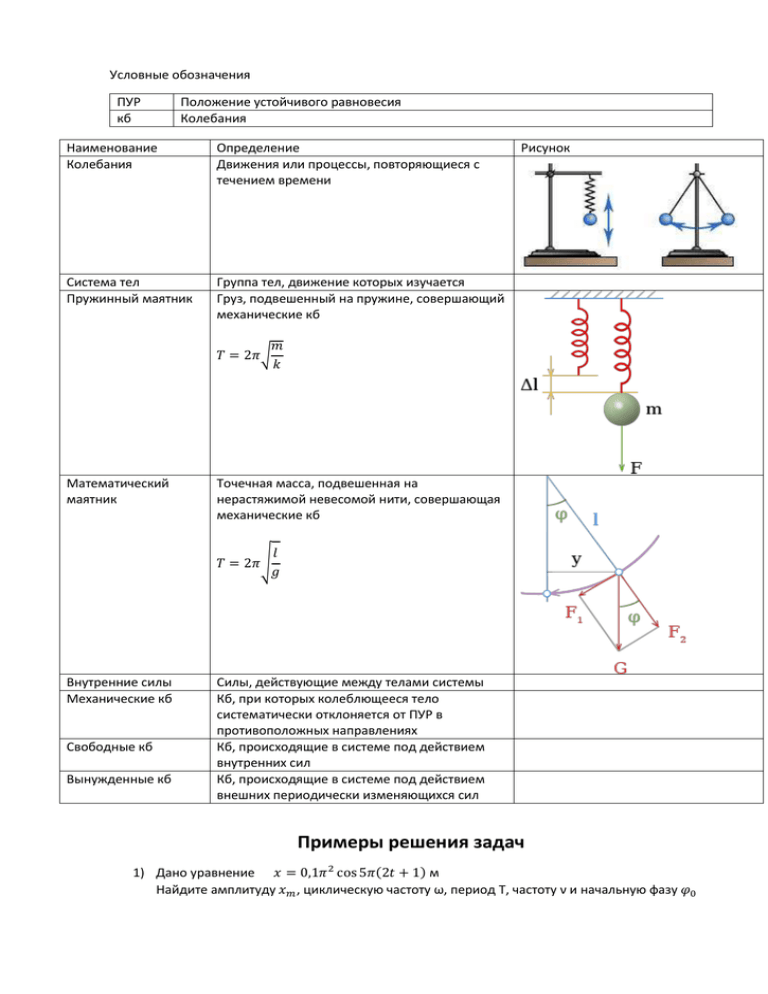
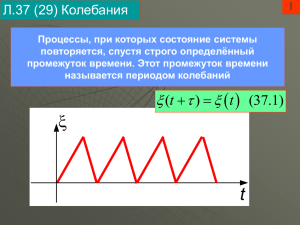
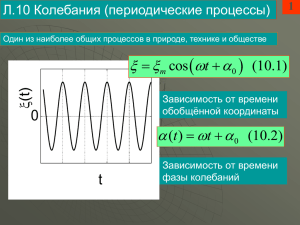
Условные обозначения ПУР кб Положение устойчивого равновесия Колебания Наименование Колебания Определение Движения или процессы, повторяющиеся с течением времени Система тел Пружинный маятник Группа тел, движение которых изучается Груз, подвешенный на пружине, совершающий механические кб Рисунок 𝑚 𝑘 𝑇 = 2𝜋√ Математический маятник Точечная масса, подвешенная на нерастяжимой невесомой нити, совершающая механические кб 𝑙 𝑇 = 2𝜋√ 𝑔 Внутренние силы Механические кб Свободные кб Вынужденные кб Силы, действующие между телами системы Кб, при которых колеблющееся тело систематически отклоняется от ПУР в противоположных направлениях Кб, происходящие в системе под действием внутренних сил Кб, происходящие в системе под действием внешних периодически изменяющихся сил Примеры решения задач 1) Дано уравнение 𝑥 = 0,1𝜋 2 cos 5𝜋(2𝑡 + 1) м Найдите амплитуду 𝑥𝑚 , циклическую частоту ω, период T, частоту ν и начальную фазу 𝜑0 Резонанс Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний Автоколебания Незатухающие кб, которые могут существовать в системе без воздействия на неё внешних периодических сил Периодические изменения физической величины в зависимости от времени по закону sin или cos Гармонические кб Период T Частота ν Циклическая частота ω Амплитуда Xmax Минимальный промежуток времени, через который движение тела полностью повторяется. Единица измерения [T]= 1 с(секунда) Число колебаний в единицу времени. Единица измерения [ν]= 1 Гц(Герц) Число колебаний тела, но не за 1 с, а за 2π с 𝑥 = 𝑥𝑚 cos(𝜔𝑡 + 𝜑0 ) 1 𝑡 2𝜋𝑅 𝑇= = = 𝜈 𝑁 𝑉 1 𝑁 𝑉 = = 𝑇 𝑡 2𝜋𝑅 𝑉 𝑎 2𝜋 𝜔 = = √ = 2𝜋𝜈 = 𝑅 𝑅 𝑇 𝜈= Модуль наибольшего смещения тела от положения равновесия. Единица измерения [Xmax]= 1 м(метр) Фаза кб ϕ Аргумент периодически изменяющейся функции, описывающей колебательный процесс. Единица измерения [ϕ]= 1 (радиан) Начальная фаза кб ϕ0 Скорость V Ускорение a Фаза в момент времени t=0 Первая производная координаты Вторая производная координаты Решение: Сперва раскроем скобки 𝑥 = 0,1𝜋 2 cos(10𝜋𝑡 + 5𝜋) м 𝑉 = 𝑥 ′ = −𝜔0 𝑥𝑚 sin(𝜔0 𝑡 + 𝜑0 ) 𝑎 = 𝑉′ = −𝜔2 𝑥𝑚 cos(𝜔0 𝑡 + 𝜑0 ) 𝑉2 𝑎 = 𝜔2 𝑅 = 𝑅 Теперь запишем уравнение 𝑥(𝑡) в общем виде 𝑥 = 𝑥𝑚 cos(𝜔𝑡 + 𝜑0 ) Из сравнения этих уравнений следует, что выражение 0,1𝜋 2 , стоящее между знаком равенства и обозначением cos, есть амплитуда 𝑥𝑚 . Выражение 10𝜋 , стоящее между скобкой и временем 𝑡, есть циклическая частота колебаний ω. Так как 𝜔 = 2𝜋 𝑇 2 с = 0,2 с. 10 1 = = 5 Гц 0,2 , то 𝑇 = 1 𝑇 Поскольку 𝜈 = , то 𝜈 Выражение 5π в скобках, в которое не входит текущее время t , есть начальная фаза колебаний 𝜑0 . 2) Частица совершает гармонические колебания вдоль оси OX около положения равновесия. Циклическая частота колебаний частицы ω = 4 рад/с. В какой момент времени t после прохождения положения равновесия частица будет иметь координату x = 25 см и скорость v = 100 см/с ? Решение: начало отсчёта времени колебаний ведется от момента, когда координата частицы равна нулю. Значит колебания частицы происходят по закону синуса. 𝑥 = 𝑥𝑚 sin 𝜔𝑡 Поскольку нам известна скорость частицы в момент времени t, запишем уравнение скорости 𝑉 = 𝑥 ′ = 𝜔𝑥𝑚 cos 𝜔𝑡 𝑥 𝑥 Разделив первое уравнение на второе получим 𝑉 = 𝜔𝑥𝑚 sin 𝜔𝑡 𝑚 cos 𝜔𝑡 𝑡= откуда 𝑡𝑔 𝜔𝑡 = 𝑥𝜔 𝑉 1 𝑥𝜔 1 25 ∗ 4 𝜋 𝑎𝑟𝑐𝑡𝑔 ( ) = 𝑎𝑟𝑐𝑡𝑔 ( ) = ≈ 0,2 с 𝜔 𝑉 4 100 8 3) Если к шарику массой 𝑚1 , колеблющемуся на пружине, подвесить снизу еще один шарик массой 𝑚2 = 300г , то частота колебаний уменьшится в 𝑛 = 2 раза. Чему равно масса 𝑚1 первого шарика? Решение: 𝑛= 𝜈1 , 𝜈2 𝑛= где 𝜈1 = 1 𝑘 √ 2𝜋 𝑚1 1 𝑘 √ 2𝜋 𝑚1 + 𝑚2 1 𝑘 √ 2𝜋 𝑚1 𝜈2 = 1 𝑘 √ 2𝜋 𝑚1 + 𝑚2 (𝑚1 + 𝑚2 ) 𝑘(𝑚1 + 𝑚2 ) =√ =√ 𝑚1 𝑘 𝑚1 𝑛2 = 𝑚1 = (𝑚1 + 𝑚2 ) 𝑚2 =1+ 𝑚1 𝑚1 𝑚2 0,3 = = 0,1 кг −1 4−1 𝑛2