MS PowerPoint, 410 Кб
реклама
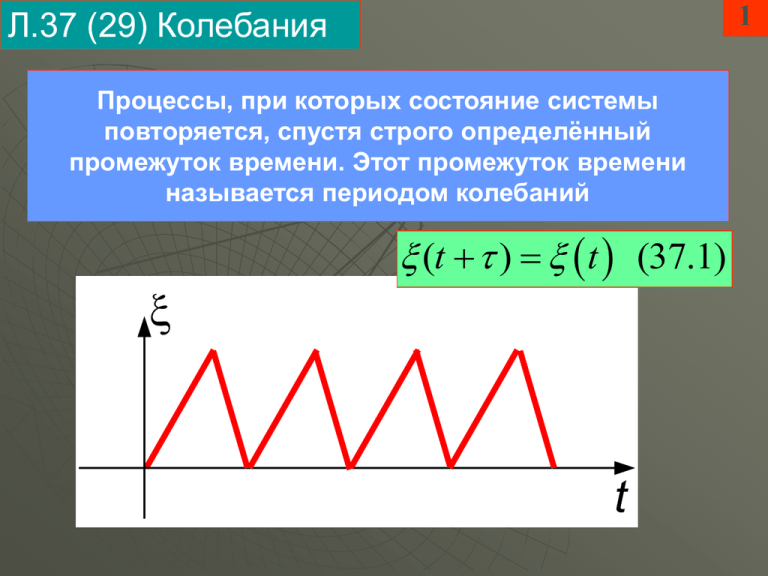
1 Л.37 (29) Колебания Процессы, при которых состояние системы повторяется, спустя строго определённый промежуток времени. Этот промежуток времени называется периодом колебаний (t ) t (37.1) t 6. Дифференциальное уравнение свободных гармонических колебаний и его решение m k 0 (6.1) Динамическое уравнение 0 (6.2) Кинематическое уравнение 2 0 m cos(0t 0 ) (6.3) 0 k / m 1/ 2 m , 0 (6.4) Решение – закон косинуса СЧ ГО Амплитуда и начальная фаза определяются НУ 0 ,0 2 График зависимости обобщённой координаты от времени при свободных и вынужденных гармонических колебаниях 3 (t) (t ) t 0 (10.2) 0 Зависимость от времени фазы любых колебаний t 4 7. Дифференциальное уравнение затухающих колебаний и его решение m r k 0 (7.1) 2 02 0 (7.2) Динамическое уравнение Кинематическое уравнение m0 exp t cos(d t 0 ) (7.3) r (7.4) 2m m 0 , 0 Решение – закон, по которому совершаются ЗК Коэффициент затухания Начальная амплитуда и начальная фаза определяются НУ 0 ,0 Затухающие колебания: ближе к реальности, чем свободные; консервативный + инерционный + диссипативный элементы (демонстрации) (t) m 2 k 2 W (t ) (37.2) 2 2 0 Энергия ГО при затухающих колебаниях убывает со временем, переходя во внутреннюю энергию среды - диссипация Зависимость от времени обобщённой координаты при затухающих колебаниях t 5 Практически наиболее интересны слабозатухающие колебания 0 (37.3) Коэффициент затухания много меньше собственной частоты W 0 t W t (37.4) r 0 (37.5) 1 6 Убыль энергии за один период много меньше энергии осциллятора в данный момент Время релаксации много больше периода колебаний Логарифмический декремент затухания (ЛДЗ) и добротность – удобные безразмерные характеристики диссипативных свойств осциллятора m t ln m t 0 Q 2 W t W 0 t 0 Q 7 Определение ЛДЗ Определение добротности Связь ЛДЗ с коэффициентом затухания и периодом Связь ЛДЗ с добротностью 0 10 8. Дифференциальное уравнение вынужденных колебаний и его решение Fm 2 cos(t ) (8.1) m 2 0 Дифференциальное уравнение ВК mf cos t f ( ) (8.2) Решение – закон ВК 1/ 2 2 Fm 2 2 2 2 mf 4 (8.3) 0 m 2 tg[ f ( )] 2 (8.4) 2 0 Амплитуда ВК (АЧХ) Разность фаз ВВС и ВК (ФЧХ) 12 Вынужденные колебания: резонансная кривая – зависимость амплитуды от частоты ВВС (АЧХ) 1 2 mf Q1 Q2 1 1 2 0 Резонанс – резкое возрастание амплитуды ВК при приближении частоты ВВС к СЧ ГО (демонстрации) 2 Q Глядя на резонансную кривую сразу можно прикинуть добротность 0 Вынужденные колебания: резонансная кривая – зависимость амплитуды от частоты ВВС (АЧХ) 2 0 m mf mf 0 Другое определение добротности Fm 0 Q 2 Fm mf 0 2 0 m mf 0 Q mf 0 0 1 2 Q1 Q2 14 9. Резонанс Физическое явление. Заключается в резком возрастании амплитуды вынужденных колебаний при совпадении СЧ и частоты ВВС Физическая причина резонанса в том, что фазы ВВС и обобщённой скорости всё время совпадают, мощность ВВС всё время положительна mf 0 16 18 Метод векторных диаграмм позволяет наглядно и эффективно анализировать колебания: анимация из Открытой физики mf cos t f ( ) как бы катет, если mf - гипотенуза mf sin t f ( ) тоже как бы катет, если mf - гипотенуза Это мотивация использования «как бы» векторов для анализа колебательных процессов Рецепт построения векторных диаграмм Каждое слагаемое-колебание - стрелка Амплитуда колебания – длина стрелки Фаза колебания – угол между положительным направлением горизонтальной оси и стрелкой, положительный – против часовой стрелки 22 mf Fm 2 cos(t ) m 2 2 0 24 2 mf Fm m t0 mf 02 mf cos t f ( ) 26 Векторная диаграмма вынужденных колебаний для случая резонанса Fm 2 cos(t ) m 2 0 mf 2 mf 02 mf cos t f ( ) 2 mf Fm m 2 tg[ f ( )] 2 2 0 1/ 2 2 Fm 2 mf 02 4 2 2 m Пример использования вынужденных колебаний и резонанса: приём радиосигнала 28 Пример учёта вынужденных колебаний и резонанса: СЧ конструкций должны быть подальше от частот возможных периодических воздействий Пример катастрофического резонанса: совпадение СЧ зданий с частотой землетрясения – Спитак, 7.12.1988, около 50 тыс. погибших, около 500 тыс. человек остались без крова (Природа, 1998, ) Если хотите добиться максимального эффекта воздействия с минимальными усилиями – воздействуйте в резонанс, на СЧ Если хотите добиться минимального эффекта воздействия – держитесь подальше от СЧ