ИДЗ №1
реклама
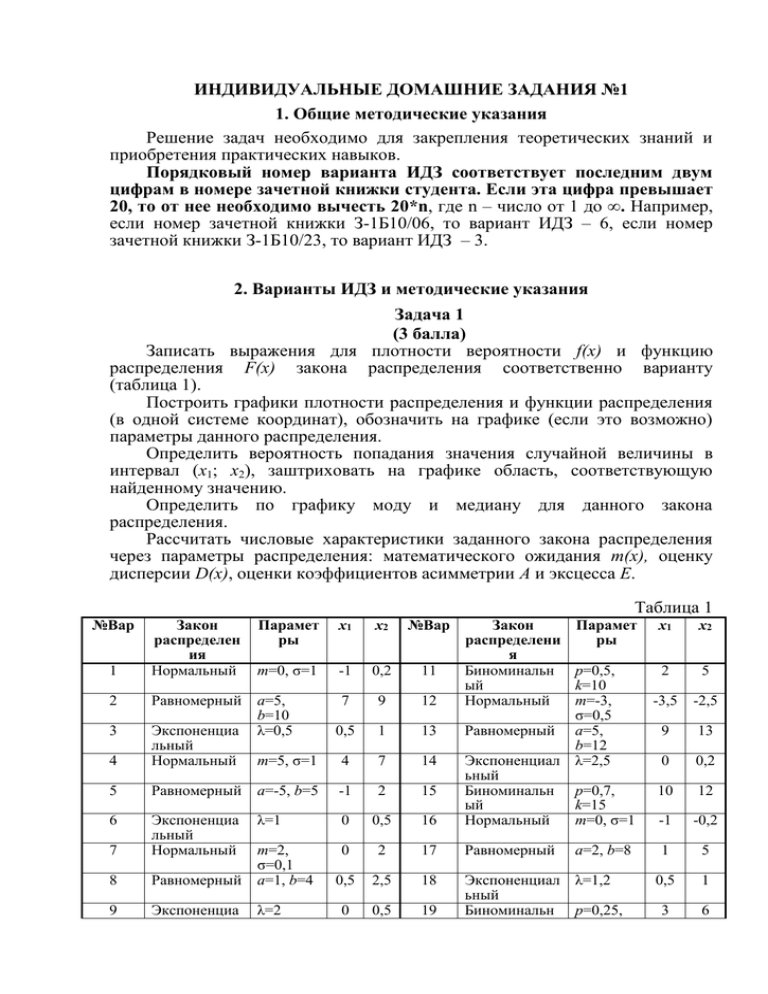
ИНДИВИДУАЛЬНЫЕ ДОМАШНИЕ ЗАДАНИЯ №1 1. Общие методические указания Решение задач необходимо для закрепления теоретических знаний и приобретения практических навыков. Порядковый номер варианта ИДЗ соответствует последним двум цифрам в номере зачетной книжки студента. Если эта цифра превышает 20, то от нее необходимо вычесть 20*n, где n – число от 1 до ∞. Например, если номер зачетной книжки З-1Б10/06, то вариант ИДЗ – 6, если номер зачетной книжки З-1Б10/23, то вариант ИДЗ – 3. 2. Варианты ИДЗ и методические указания Задача 1 (3 балла) Записать выражения для плотности вероятности f(x) и функцию распределения F(x) закона распределения соответственно варианту (таблица 1). Построить графики плотности распределения и функции распределения (в одной системе координат), обозначить на графике (если это возможно) параметры данного распределения. Определить вероятность попадания значения случайной величины в интервал (x1; x2), заштриховать на графике область, соответствующую найденному значению. Определить по графику моду и медиану для данного закона распределения. Рассчитать числовые характеристики заданного закона распределения через параметры распределения: математического ожидания m(x), оценку дисперсии D(x), оценки коэффициентов асимметрии А и эксцесса Е. Таблица 1 №Вар 1 Закон распределен ия Нормальный Парамет ры x1 x2 №Вар m=0, σ=1 -1 0,2 11 a=5, b=10 λ=0,5 7 9 12 0,5 1 13 m=5, σ=1 4 7 14 Закон распределени я Биноминальн ый Нормальный Парамет ры x1 x2 2 Равномерный 3 4 Экспоненциа льный Нормальный 5 Равномерный a=-5, b=5 -1 2 15 6 λ=1 0 0,5 16 7 Экспоненциа льный Нормальный p=0,5, k=10 m=-3, σ=0,5 Равномерный a=5, b=12 Экспоненциал λ=2,5 ьный Биноминальн p=0,7, ый k=15 Нормальный m=0, σ=1 2 5 -3,5 -2,5 9 13 0 0,2 10 12 -1 -0,2 0 2 17 Равномерный 8 Равномерный m=2, σ=0,1 a=1, b=4 1 5 0,5 2,5 18 9 Экспоненциа λ=2 0 0,5 19 Экспоненциал λ=1,2 ьный Биноминальн p=0,25, 0,5 1 3 6 a=2, b=8 №Вар 10 Закон распределен ия льный Нормальный Парамет ры x1 x2 №Вар m=4, σ=2 2 4 20 Закон Парамет распределени ры я ый k=7 Нормальный m=0,5, σ=2 x1 x2 1 2,5 Задача 2 (3 балла) В таблице. 2 (по вариантам) представлен вариационный дискретный ряд случайной величины X. Построить полигон и гистограмму относительных частот (выбирая xi, за центры интервалов), определить оценку математического ожидания m, оценку дисперсии S2, оценки коэффициентов асимметрии А и эксцесса Е. Построить доверительный интервал для математического ожидания m и доверительный интервал для дисперсии σ2 для имеющейся выборки. Таблица 2 №Вар 1 2 3 4 5 6 7 8 9 10 №Вар xi 5 10 ni 4 6 xi 130 140 ni 5 10 xi 25 30 ni 8 12 xi 30 40 ni 10 20 xi 24 26 ni 6 15 xi 0 2 ni 6 9 xi 10 15 ni 5 10 xi 15 18 ni 6 8 xi -7,5 -5 ni 2 3 xi 45 50 ni 2 3 15 10 150 25 35 20 50 60 28 56 4 15 20 30 21 12 -2,5 6 55 5 20 40 160 30 40 80 60 50 30 17 6 60 25 25 24 42 0 18 60 20 25 20 170 15 45 40 70 30 32 3 8 30 30 15 27 17 2,5 12 65 10 30 12 180 10 50 24 80 20 34 2 10 18 35 10 30 10 5 6 70 6 35 8 190 5 55 16 90 10 36 1 12 12 40 5 33 5 7,5 3 75 4 11 12 13 14 15 16 17 18 19 20 xi ni xi ni xi ni xi ni xi ni xi ni xi ni xi ni xi ni xi ni 0,5 6 1 10 10 2 -1,5 15 -30 6 15 6 -15 5 2 5 20 10 -5 5 1 10 2 17 20 6 -1 12 -20 15 25 9 -10 10 4 10 40 20 -4 10 1,5 12 3 22 30 4 -0,5 10 -10 56 35 15 -5 25 6 25 60 60 -3 12 2 2,5 3 14 13 11 4 5 6 25 18 20 40 50 60 10 8 7 0 0,5 1 13 17 15 0 10 20 17 3 2 45 55 65 60 30 18 0 5 10 30 15 10 8 10 12 30 15 10 80 100 120 50 30 20 -2 -1 0 14 4 3 3,5 4 7 13 70 3 1,5 18 30 1 75 12 15 5 14 5 140 10 1 2 Задача 3 (2 балла) Задачи выбирается по вариантам в соответствии с таблицей. 3. Таблица 3 №Вар 1 2 3 4 5 6 7 8 9 10 № Параметры №Вар № Параметры задачи задачи 1 x1=6,8; x2=7,3; n1=20; n2=8; 11 4 x=1,56%; S=0,52%; n=25; S1=0,08; S2=0,6; P=0,9 m0=1,5%; P=0,95 2 2 7 σ0 =8,8; S =8,4; n=32; 2 x1=106,4; x2=102,3; n1=15; P=95% n2=17; σ=1,8; P=0,95 2 x1=8,01; x2=9,35; n1=25; 12 5 x=104,3мм; σ0=0,75мм; n2=55; σ=0,3; P=0,96 n=15; m0=105мм; α=0,02 6 n1=11; n2=12; S12=15,4; 3 – 2 S2 =12,8; P=95% 3 – 13 6 n1=11; n2=12; S12=15,4; S22=12,8; P=99% 5 x=54,23мм; σ0=0,75мм; 1 x1=27,8; x2=31,4; n1=14; n=15; m0=55мм; α=0,05 n2=18; S1=1,2; S2=1,8; P=0,9 4 x=0,78%; S=0,015%; n=10; 14 7 σ02=0,23; S2=0,38; n=30; m0=0,8%; P=0,9 P=95% 6 n1=17; n2=14; S12=62,4; 2 x1=54,9; x2=55,1; n1=12; 2 S2 =63,8; P=95% n2=18; σ=0,7; P=0,95 5 x = 12,4 мм; σ0=0,1 мм; n = 15 1 x1=10,5; x2=6,4; n1=15; 54; m0=12,3 мм; α=0,01 n2=10 S1=0,8; S2=0,6; P=0,99 1 x1=6,8; x2=7,3; n1=20; n2=8; 7 σ02=2,7; S2=2,54; n=14; S1=0,08; S2=0,6; P=0,9 P=98% 6 n1=16; n2=19; S12=8,5; 16 2 x1=104,6; x2=104,3; n1=25; 2 S2 =6,3; P=95% n2=10; σ=0,5; P=0,9 2 x1=41,7; x2=43,1; 6 n1=13; n2=18; S12=0,23; n1=14; n2=27; σ=0,3; S22=0,47; P=95% P=0,96 7 σ02=0,15; S2=0,25; n=25; 17 4 x=1,5%; S=0,5%; n=12; P=98% m0=1,2%; P=0,95 1 x1=6,8; x2=7,3; n1=10; 3 – n2=18; S1=0,8; S2=0,6; P=0,95 1 x1=6,8; x2=7,3; n1=15; n2=8; 18 5 x=104,3мм; σ0=1,1мм; S1=0,7; S2=1,2; P=0,95 n=12; m0=105мм; α=0,05 5 x=64,7мм; σ0=1,7мм; n=17; 2 x1=89,4; x2=86,5; m0=64мм; α=0,05 n1=8; n2=11; σ=2,2; P=0,95 2 x1=15,6; x2=14,7; n1=10; 19 6 n1=9; n2=16; S12=26,4; n2=15; σ=1,2; P=0,9 S22=18,9; P=95% 2 6 n1=16; n2=24; S1 =36,4; 1 x1=27,8; x2=25,3; n1=9; 2 S2 =32,9; P=99% n2=12; S1=0,9; S2=1,1; P=0,95 3 – 20 7 σ02=4,8; S2=5,4; n=26; P=95% 7 σ02=0,7; S2=0,64; n=31; 3 – P=95% 1. Для увеличения надежности была разработана новая конструкция измерительного прибора. Средняя наработка на отказ прибора прежней конструкции в n1 испытаниях составила в среднем x1 месяцев со средним квадратическим отклонением S1 месяца. Приборы новой конструкции при n2 испытаниях проработали в среднем x2 месяца со средним квадратическим отклонением S2 месяца. Требуется при доверительной вероятности P сделать вывод действительно ли новая конструкция надежнее прежней, считая, что 12 22 . 2. В результате двух серий измерений случайной величины получены следующие средние значения результатов измерения: x1; x2 (объем выборок в сериях соответственно равны: n1, n2). Можно ли объяснить расхождение между x1 и x2 случайными причинами (с вероятность P), если измерения проводилось одним прибором со среднеквадратическим отклонением σ. 3. Два ряда измерения частоты сигнала одним и тем же прибором дали следующие результаты: f1, Гц 1416 1416 1420 1420 1416 1417 1415 1418 f2, Гц 1417 1427 1418 1425 1427 1429 1427 1423 Какова вероятность того, что расхождения между результатами является случайным? 4. При проверке n экземпляров однотипных приборов выборочное среднее для приведенной погрешности оказалось равным x, а выборочное среднее квадратическое отклонение равно S. Техническими условиями на прибор данного типа оговорено, что с вероятностью P погрешность не должна превышать m0. Удовлетворяет ли техническим условиям данный тип приборов? 5. Станок-автомат вытачивает детали диаметром m0 мм со среднеквадратическим отклонением диаметра σ0 мм. Для проверки, правильно ли настроен станок, были проведены контрольные замеры n деталей и рассчитано значение диаметра x мм. При уровне значимости α определить, нуждается ли станок в перенастройке. 6. На двух токарных станках обрабатываются втулки. Отобраны две пробы: из втулок, сделанных на первом станке, n1 шт., на втором станке – n2 шт. По данным этих выборок рассчитаны выборочные смещенные дисперсии S12 (для первого станка) и S22 (для второго станка). Можно ли считать, что станки обладают различной точностью. Доверительная вероятность Р. 7. Точность работы станка-автомата проверяется по дисперсии σ02 контролируемого размера изделий, которая не должна превышать m0 . По данным из n отобранных изделий вычислена несмещенная дисперсия S 2 . Выяснить, обеспечивает ли станок требуемую точность. Доверительная вероятность P.



