Демоверсия экзаменационной работы по математике, 10 класс

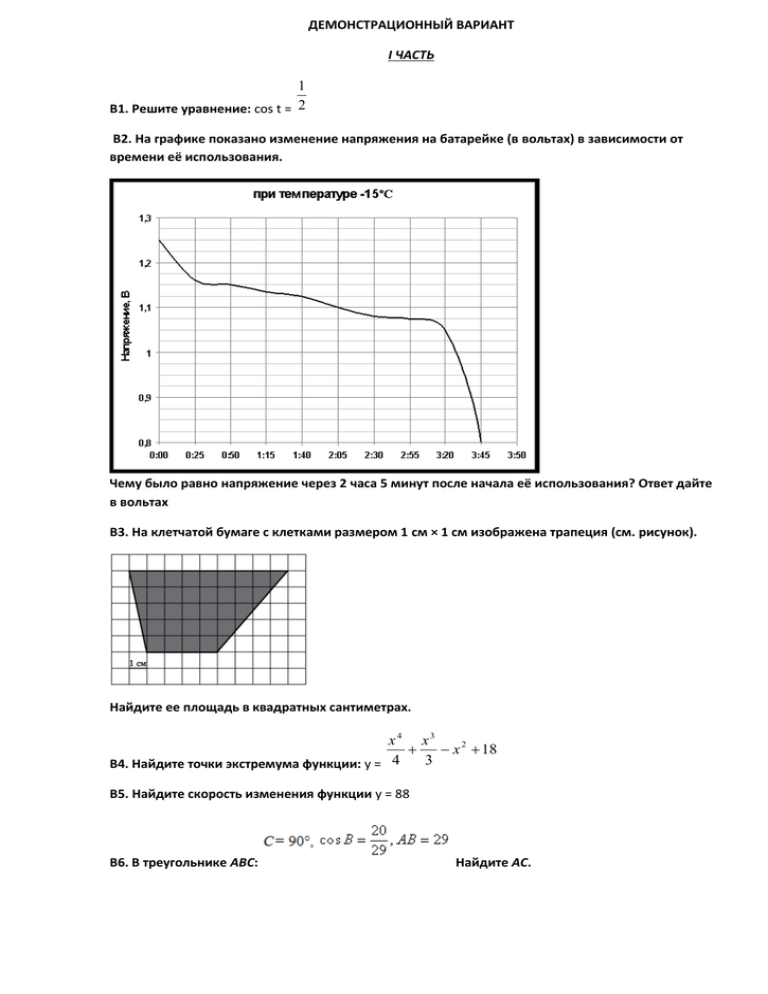
ДЕМОНСТРАЦИОННЫЙ ВАРИАНТ
I ЧАСТЬ
1
В1. Решите уравнение: cos t = 2
В2. На графике показано изменение напряжения на батарейке (в вольтах) в зависимости от
времени её использования.
Чему было равно напряжение через 2 часа 5 минут после начала её использования? Ответ дайте
в вольтах
В3. На клетчатой бумаге с клетками размером 1 см × 1 см изображена трапеция (см. рисунок).
Найдите ее площадь в квадратных сантиметрах.
x4 x3

 x 2  18
4
3
В4. Найдите точки экстремума функции: y =
В5. Найдите скорость изменения функции у = 88
В6. В треугольнике ABC:
Найдите AC.

В7. Известно,что cos t =
3 
5 , 2 < t <  . Вычислите tg t.
В8.
На рисунке изображён
график функции у=f (х)
и касательная к нему
в точке с абсциссой х0.
Найдите значение
производной функции
f (х) в точке х0.


cos  t ctg  t 
2 


sin   t 
2 
В9. Упростите выражение:
B10. Лена и Саша играют в кости. Они бросают кость по одному разу. Выигрывает тот, кто
выбросил больше очков. Если очков выпало поровну, то наступает ничья. Известно, что в сумме
выпало 8 очков. Найдите вероятность того, что Лена проиграла.
В11. Кубик весит 10г. Сколько граммов будет весить кубик, ребро которого в 3 раза больше, чем
ребро первого кубика, если оба кубика изготовлены из одного и того же материала?
2
В12. Решите неравенство: cos t < - 2
В13. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной
скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости
первого на 18 км/ч, а вторую половину пути — со скоростью 108 км/ч, в результате чего прибыл
в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если
известно, что она больше 63 км/ч. Ответ дайте в км/ч
В14. Найдите наименьшее значение функции y = 6cosx + 6x + 4 на отрезке
.
II ЧАСТЬ
С1. а) Решите уравнение 2sin3 x – 2sin x + cos2 x = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [−
𝟕𝝅
; −𝟐𝝅].
𝟐
С2.
В прямоугольном параллелепипеде
ABCDA 1 B1 C 1 D 1, у которого AB = 4, BC = 6,
CC1 = 4. Найдите тангенс угла между
плоскостями CDD1 и BDA1.
x2  4
2
С3.Постройте график функции у = x  4
С4.При каких значениях параметра а уравнение (3а - 1)х2 + 2ах + 3а – 2 = 0 имеет два
действительных различных корня?
2
С5. Решите неравенство
2
 x 2  6x  9  1 
 x  3  x  6 x  9  1 

 4






x
5

x

1
5

x

1





2
С6.Найдите все такие пары взаимно простых натуральных чисел (то есть чисел, наибольший
общий делитель которых равен 1) а и b, что если к десятичной записи числа а приписать справа
b
через запятую десятичную запись числа b, то получится десятичная запись числа, равного a .