(3.1 MБ)
реклама

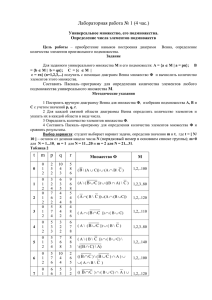
МНОЖЕСТВА ОТНОШЕНИЯ И ОПЕРАЦИИ НАД МНОЖЕСТВАМИ ДИАГРАММЫ ЭЙЛЕРА – ВЕННА Под множеством понимают, следуя основателю теории Г. Кантору, «многое, мыслимое как единое». Множество есть совокупность определенных вполне различаемых объектов (субъектов), которые называются элементами, объединенных некоторым свойством. Диаграмма Эйлера – Венна Таблица отношений и операций над множествами Определение Два множества А и В равны, если они содержат одни и те же элементы. Обозначение А=В Диаграмма Множество А есть подмножество множества В, если каждый элемент А является элементом и В. Говорят, что А включено в В. A B Дополнением множества А до универсального множества 1 называется множество A , элементы которого не принадлежат А. A Пересечением двух множеств А и В называется множество A B элементов, принадлежащих одновременно и множеству А, и множеству В. A B Объединением множеств А и В называется множество A B элементов, принадлежащих хотя бы одному из множеств А или В. A B Разностью между множествами А и В называется совокупность A B тех элементов множества А, которые не принадлежат множеству В. A B Симметрическая разность А и В есть объединение двух разностей A B и B A. A B Пример, иллюстрирующий диаграммами Эйлера – Венна справедливость следующего отношения включения: A B C A B C A B C Порядок выполнения операций: 1 2 5 6 7 3 4 A B C A B C A B C Диаграмма Эйлера – Венна 1 A B 2 A B C 3 A B 4 A B C 5 A B 6 A B C 7 A B C A B C A B C A B C A B C Пример, иллюстрирующий диаграммами Эйлера – Венна равенство множеств A B A B A B Порядок выполнения операций: A B A B A B 3 2 1 4 Диаграмма Эйлера – Венна 1 A B B A B 2 A B A B 3 4 A B