Учебная презентация (изгиб балок, эпюры)

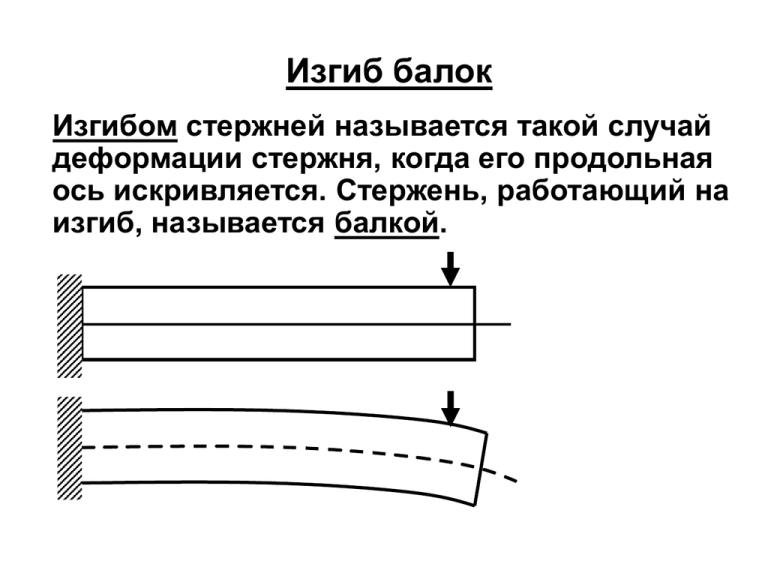
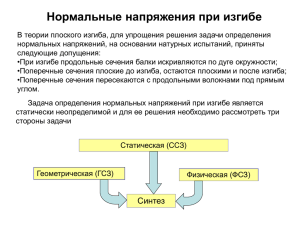
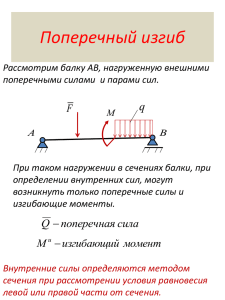
Изгиб балок
Изгибом стержней называется такой случай
деформации стержня, когда его продольная
ось искривляется. Стержень, работающий на
изгиб, называется балкой.
Будем рассматривать плоский, прямой,
поперечный изгиб:
Силовая плоскость
Р1
1. Плоский – все внешние
нагрузки лежат в одной
плоскости;
Р2
q
2. Прямой – плоскость
действия сил проходит
через главную ось
поперечного сечения;
C
x
3. Поперечный – линии
действия внешних сил 
продольной оси балки
Определим внутренние силовые факторы в
случае изгиба:
q
Р1
Р2
Рассечем балку и
рассмотрим
равновесие
отсеченной части
Р1
Для произвольного сечения:
y
z
x
Qy  0
N=0
Qz = 0
Mx = 0
My = 0
Mz  0
z
Mz
Qz
N
Mx
x
Qy
My
y
Вывод: В поперечном сечении балки при
прямом изгибе возникает поперечная сила
Qy и изгибающий момент Mz
Рассмотрим плоский рисунок:
Р1
M>0
Qy>0
Qy>0 Р2
M>0
q
Правило знаков для внутренних силовых
факторов
Поперечная сила считается положительной,
если она вращает оставшуюся часть балки
по часовой стрелке.
Изгибающий момент считается положительным, если при его воздействии растягиваются нижние волокна балки.
Правило знаков для внутренних силовых
факторов
«Компас»
M
M
Q
+
Q
Дифференциальные зависимости при
изгибе
q M+dM
y
M
Р1
q
Q
O
x
dx
x
Q+dQ
 Fky  0; Q  (Q  dQ)  qdx  0; (1)
dx
dx
dx
 M  0;  Q 2  (Q  dQ) 2  M  (M  dM )  0;
0
dx
 Qdx  dM  dQ
 0; (2)
2
dQ
dM
Из (1): q 
Из (2): Q 
dx
dx
d 2M
q
2
dx
Построение эпюр М и Q
Рассмотрим простой пример:
q
A
B
x
RB=1/2ql
RA=1/2ql
l
1. Определить
реакции опор
2. Разбить балку на
характерные участки
3. Воспольз. методом
сечений
Эп. Q
Эп. M
3. Воспользуемся методом сечений:
q
y
A
RA
c
x
M
 Fky  0;
RA  qx  Q  0
0 xl
Q  RA  qx;
x
Q
ql
при x  0, Q  R A 
2
ql
ql
при x  l , Q 
 ql   .
2
2
2
qx
 M C  0;  RA x  2 2M  0
qx
M  RA x 
; 0 xl
2
при
x  0, M  0;
при
x  l,
2
ql
ql
M  l
 0;
2
2
q
A
B
x
RB=1/2ql
RA=1/2ql
ql
2
l
+
Эп. Q
-
+
ql 2
8
ql
2
dM
Q
dx
Для нахождения
экстремума:
dM
Q
 0;
dx
ql
 qx0  0;
2
l
x0  .
2
l
Эп. M при x0  2 
2
ql l q  l 
ql 2
M
   
.
2 2 22
8
Общий порядок построения эпюр М и Q
1. Определить опорные реакции (если это необходимо)
2. Разбить балку на участки
I
II
III
IV
V
3. В пределах каждого участка провести поперечные
сечения и определить его положение
4. На каждом участке составить выражения:
Для Q – сумма проекций всех внешних сил, взятых по
одну сторону от сечения, на плоскость поперечного
сечения с учетом правила знаков;
Для М – сумма моментов всех внешних сил, взятых по
одну сторону от сечения, относительно центра тяжести
этого сечения, с учетом правила знаков;
Правило знаков для внешних сил и реакций совпадает
с правилом знаков для поперечной силы и
изгибающего момента соответственно.
5. Проанализировать полученные выражения и
построить соответствующие эпюры на участках
6. Проверить построенные эпюры по «скачкам» и на
основе дифференциальных зависимостей при изгибе
а). Скачки на эпюре Q должны быть в тех сечениях,
где приложены сосредоточенные силы,
б). Скачки на эпюре M должны быть в сечениях, где
приложены пары сил,
в). Если Q = 0 в какой-либо точке, то в этой точке М
имеет экстремум,
г). На участках с распределенной нагрузкой эпюра М
подобна парусу, если представить нагрузку как
ветер.