Сопромат. ИДЗ Поперечный изгиб

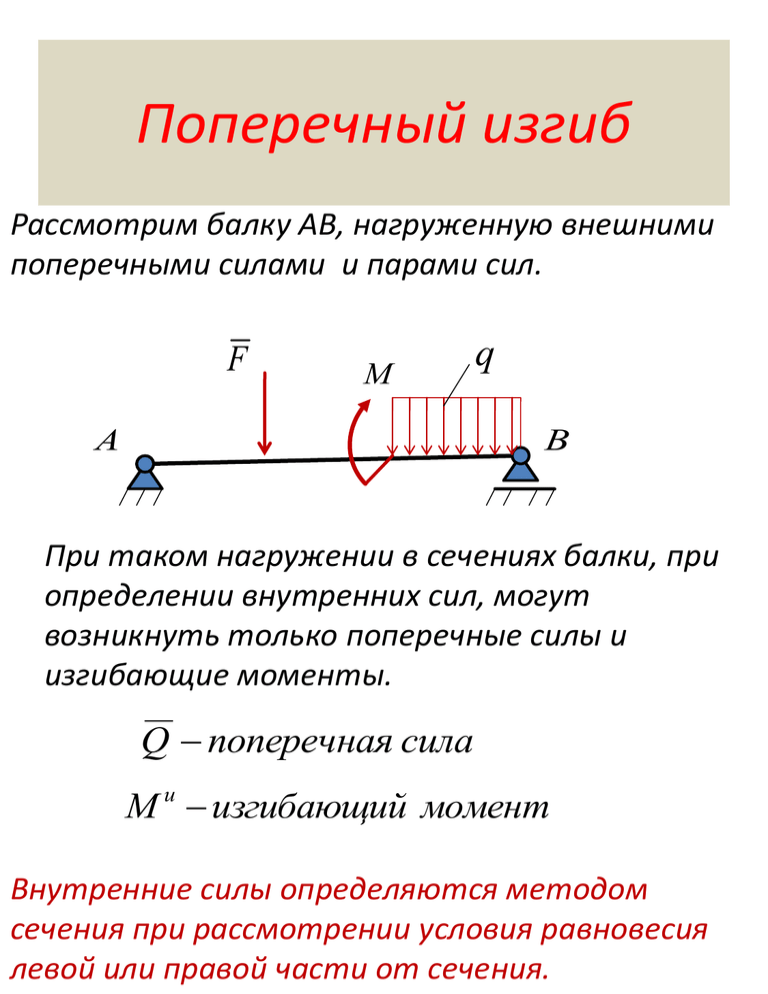
Поперечный изгиб
Рассмотрим балку АВ, нагруженную внешними
поперечными силами и парами сил.
F
M
A
q
B
При таком нагружении в сечениях балки, при
определении внутренних сил, могут
возникнуть только поперечные силы и
изгибающие моменты.
Q  поперечная сила
M и  изгибающий момент
Внутренние силы определяются методом
сечения при рассмотрении условия равновесия
левой или правой части от сечения.
Правило знаков для поперечной силы и
изгибающего момента при построении их
эпюр.
Правило знаков при построении эпюр
поперечных сил
Левая часть от сечения
Q
Правая часть от сечения
Q
Сила
Q
пытается повернуть балку по часовой стрелке.
Правило знаков при построении эпюр
изгибающих моментов
Mи
+
Mи
Изгибающий
и
момент
пытается изогнуть
балку выпуклостью
вниз – направлен в
балку.
M
-
Пример: Консольная балка АВ нагружена
сосредоточенной силой F, распределенной нагрузкой,
интенсивностью q, и парой с моментом М.
Дано: F=10н; q=10н/м; М=10нм; а=0,4м; в=0,6м; с=0,8м.
Построить эпюры внутренних сил (поперечных сил и
изгибающих моментов)
q
M
F
B
A
c
a
b
1. Определим силы реакции глухой заделки
в точке А: XA; YA; MA из уравнений равновесия.
R  q  a  4н
xA  0
Расчетная схема
yA M A
xA
R
M
F
A
B
c
y
i
m
A
b
a
2
a
2
 y A F  R  0; y A  6н
 mA  F  c  M  R(c  b  a2 )  0; M A  8,4нм
Проверка:
yA M A
F
YA=6н
МА=8,4нм
R
M
A
B
c
a
2
b
a
2
a
m

R
 B 2  M  F ( a  b)  M A  y A ( a  b  c ) 
 0,8  10  10  8,4  10,8  0
b
c
yA
MA
A
F
D
x1
x2
a
q
M
B
K
x2
0  x1  c
Балку АВ разобьем на
силовые участки
AD; DK; KB
и сделаем сечения
0  x2  b
0  x3  a
yA M A
M и1
A
O1
Q1
x1
y
i
  y A  Q1  0;
Q1   y A  6
m
o1
 M и1  M A  y A  x1  0
M и1   M A  y A  x1  8,4  6 x1 (прямая )
и
x1  0; M 1  8,4
и
x2  0.8; M 1  13,2
Q1  6
M и1  8,4
M и1  13,2
F
yA M A
M и2
O2
A
c
y
i
x2
Q2
  y A  F  Q2  0;
Q2   y A  F  4
и
m

M
2  M A  y A  (c  x2 )  F  x2  0
 o2
M и 2   M A  y A  (c  x2 )  F  x2 
 8,4  4,8  6  x2  10 x2  13,2  4  x2 (прямая )
Q2  4  const
и
x2  0; M 2  13,2
и
x2  0.6; M 2  10,8
M
и
Q3
3
y
q
m
M
и
3
x3  0; Q3  0
x3  0,4; Q3  4
x3
o3
 Q3  10  x3  0
Q3  10 x3  прямая
B
O3
i
 M
 q 
x3  0; M
и
3
x3  0,4; M
и
x3 2
2
3
 q  x3 
x3
2
 5 x3  парабола
2
0
и
3
0
 0,8
x3  0; Q3  0; M и 3  0
x3  0,4; Q3  4; M и 3  0,8
Построение
эпюр
Q1  6
x3  0; M
и
1
 8,4
Q2  4
x3  0;
x3  0;
Q3  0; M и 3  0
M и 2  13,2
x3  0,6;
x3  0,4;
Q3  4; M и 3  0,8
и
M
2  10,8
x3  0,8; M 1  13,2
и
yA
F
MA
q
M
A
B
4
4
Q
(+)
0
(-)
6
6
Mи
0
(-)
0,8
8.4
10,8
13,2
Свойства эпюр поперечных сил и
изгибающих моментов.
Свойства эпюры поперечных сил
1. В сечениях, где приложены сосредоточенные силы,
скачок на величину этой силы.
2. На участке, где нет распределенной нагрузки,
функция поперечной силы представляет собой константу.
3. На участке, где есть распределенная нагрузка, функция
поперечной силы изменяется по линейному закону.
Свойства эпюры изгибающих моментов
1. В сечениях, где приложены сосредоточенные моменты,
скачок на величину этого момента.
2. На участке, где нет распределенной нагрузки, функция
изгибающего момента изменяется по линейному закону.
3. На участке, где есть распределенная нагрузка,
функция изгибающего момента изменяется по закону
квадратичной параболы, выпуклость параболы
направлена навстречу распределенной нагрузки.
4. В сечениях, где приложены сосредоточенные силы, на
эпюре изгибающего момента наблюдается излом.
5. В сечении, где поперечная сила пересекает нулевую ось,
функция изгибающего момента имеет экстремум,.
Экстремум находим из
условия
dM и
dx
Q0
q
1
M
6.
F
c
2
b
7
q
F
c
M
3
M
A
c
A
A
c
q
F
b
F
c
M
b
a
F
M
A
c
10
A
a
b
q
a
q
q
M
9.
M
A
c
a
b
F
c
a
b
F
M
8
q
F
a
b
q
a
b
M
c
a
A
5
F
A
A
4
q
b
M
F
a
q
A
c
b
a
11
q
F
A
12
b
M
M
q
b
a
A
c b
a
M
q
F
c
18
q
M
A
c b
q
F
c F b
a
M
A
c b
15
a
b
F
A
14
M
17
F
13
F
c
a
q
A
q
A
M
c
16
q
M
19
q
F
a
M
A
a
c
F
A
20
a
b
q
M
A
c b
a
c
b a
F
21
q
26
M
A
c
22
b
F
c
q F
M
A
c bF
a
23
28
M
c F b
a
c b
29
M
A
c F b
q
q
a
M
F
A
a
c
A
F
a
a
b
30
M
c b
q
M
A
F
q
a
b
c
q
A
25
a
b
27
A
24
F M
A
a
q
M
q
q
M
A
c
F
b a