МБОУ «Средняя общеобразовательная русско-татарская школа № 14» Вахитовского района г. Казани
реклама

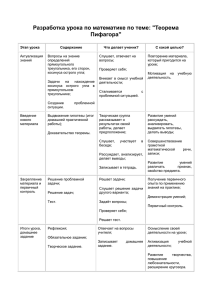
МБОУ «Средняя общеобразовательная русско-татарская школа № 14» Вахитовского района г. Казани Подготовила: учитель математики 1 категории Горшкова Г.А. Содержание 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. Цели урока Актуализация знаний Тест 1 Проверь себя! Тест 2 Пифагор О теореме Пифагора Теорема Пифагора Доказательство теоремы Минута релаксации Тренировочные упражнения Индийская задача Решение задачи Решение задачи из пособия Домашнее задание Итог урока Цели урока • Закрепление и совершенствование знаний и умений, приобретенных на предыдущих уроках • Знакомство с биографией Пифагора и историей создания теоремы • Доказательство теоремы Пифагора • Научить применять теорему Пифагора к решению задач • Показать красоту науки математики через решение древнеиндийских задач изложенных в стихах • Активизация и развитие познавательных и творческих способностей учащихся 1.Какой треугольник называется прямоугольным? 2.Какие стороны прямоугольного треугольника называются катетами? 3.Что называется косинусом острого угла прямоугольного треугольника? М 1.Какой треугольник изображен на рисунке? 2.Назовите катеты и гипотенузу этого треугольника 3.Выразите соs M, cos P К Р тест 1.Сумма углов прямоугольного треугольника 180° 2.Гипотенуза в прямоугольном треугольнике больше любого отдельно взятого катета 3.Косинус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе 4.Косинус острого угла прямоугольного треугольника всегда зависит от градусной меры угла 5.Сумма острых углов прямоугольного треугольника больше 90° 6.В равнобедренном прямоугольном треугольнике катет и гипотенуза равны Проверь себя! 1. + 2. + 3. 4. + 5. 6. - (580 г. до н. э.- 500 г. до н.э.) Жил в Древней Греции. Много путешествовал, изучая древнюю культуру и достижения науки других стран. Организовал кружок, членами которого было сделано много важных научных открытий. С его именем связано немало легенд. Пребудет вечной истина, как скоро Всё познает слабый человек! И ныне теорема Пифагора Верна,как и в его далёкий век. Обильно было жертвоприношение Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За свет луча, пришедший с облаков. Поэтому всегда с тех самых пор Чуть истина рождается на свет, Быки ревут, её почуя, вслед. Они не в силах свету помешать, А могут лишь, закрыв глаза дрожать От страха,что вселил в них Пифагор. /А.Шамиссо/ За 8 веков до н.э. эта теорема была известна индейцам под названием «правила веревки» и использовалась ими для построения алтарей, которые по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта Доказательство самого Пифагора до нас не дошло. В настоящее время имеется свыше 100 различных доказательств теоремы. Возможно, что одно из них принадлежит самому Пифагору или его ученику. Во времена Пифагора теорема звучала так: «Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах». Из-за чертежей, сопровождавших теорему Пифагора, учащиеся называли её «ветряной мельницей», составляли стихи вроде «Пифагоровы штаны во все стороны равны», рисовали карикатуры. Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов S a² + b² = c² P а c K KP² =KS² + SP² b Дано: С ∆ АВС-прямоугольный Доказать: АВ² = АС² + ВС² Доказательство: А Д В 1.Рассмотрим ∆АВС. cos A= AC/AB, cos B= BC/AB 2.СД- высота 3. Рассмотрим ∆АСД. cos A = AD/AC 4.Рассмотрим ∆ВСД сos B=ВД/ВС 5.АС/АВ=АД/АС АС² =АВ*АД ВС/АВ=ВД/ВС ВС²=АВ*ВД 6. АС² +ВС² =АВ*АД + АВ* ВД Так как АД+ВД=АВ, то АС² + ВС² = АВ*АВ АС² +ВС² =АВ² Составьте по рисунку, используя теорему Пифагора (если это возможно), верное равенство c² = a² + b² х5 3 Такой треугольник называют «египетским» 4 x² = 3² + 4² x=5 6 d² = 6² + 8² d=10 . О 8 d c² = a² + b² 3 x 5 x² ≠ 5² - 4²,т.к. треугольник не является прямоугольным a Верно ли равенство при a=1, b=2, c=3 ? c b ВЫВОД: теорема Пифагора применяется только в прямоугольном треугольнике а c b c² = a² + b² У древних индусов был обычай: задачи предлагать в стихах. Вот одна из задач индийского математика XΙΙ века Бхаскары. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в том месте река В 4 лишь фута была широка. Верхушка склонилась у края реки. Осталось 3 фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота? 3 4 х² =3² + 4² х=5 х h= x+3 h = 5+3 h h=8 х 3 4 Решение задачи из пособия «Шаг за шагом», стр.44 х² =13² - 12² x х=5 12 13 Домашнее задание: П.63, 64, № 2(3), 4 Теорема Пифагора- одна из главных и, можно сказать, самая главная теорема геометрии. Значение её состоит в том, что из неё или с помощью её можно вывести большинство теорем геометрии. Теорема Пифагора замечательна и тем, что сама по себе она вовсе и не очевидна. Например, свойства равнобедренного треугольника можно увидеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никогда не увидишь, что между его сторонами есть простое соотношение: с² = а² + b² Всем спасибо за работу! Молодцы!