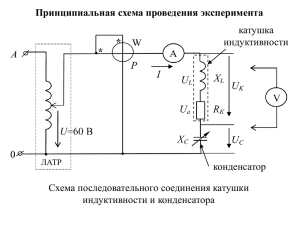
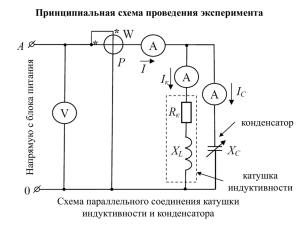
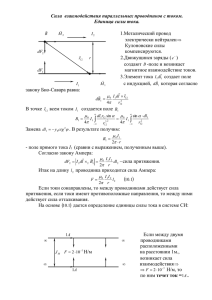
Математические модели в заземлении и ЭМС
реклама

4 Российская конференция по молниезащите при поддержке СПб 28 мая 2014 г Математические модели и методы в задачах заземления и ЭМС Шишигин С.Л. д.т.н., зав. кафедрой электротехники Мещеряков В.Е, Шишигин Д.С. аспиранты Вологодский государственный университет ЦЕПНО-ПОЛЕВАЯ МОДЕЛЬ ЗАЗЕМЛЯЮЩЕГО УСТРОЙСТВА Расчет ЗУ - нахождение z, U, I, J (цепная задача); φ, E, H (полевая задача) МЕТОДИКА G, C, M, r, L GУ =B·G·BT, CУ =B·C·BT I, J 1. Дробление на элементы 2. Расчет интегральных параметров: проводимости растекания G, индуктивности M, емкости C, внутреннего сопротивления r и индуктивности стержней L 3. Перенос матриц G,C в узлы схемы замещения GУ=B·G·BT, CУ=B·C·BT, где bi,j = 0.5|ai,j |, А – матрица соединений продольных ветвей 4. Расчет продольных токов I, стекающих токов J токов, напряжений ветвей и входного сопротивления 5. Расчет потенциала φ, напряженности E, H Вывод: Простая и адекватная математическая модель 2 ДВУХСЛОЙНАЯ 1D-МОДЕЛЬ ЗЕМЛИ Метод зеркальных отображений стержня от двух плоских границ Рис.1. Источник в верхнем слое (а), расчетная точка в верхнем (б) и нижнем (в) слое земли Рис.2. Источник в нижнем слое (а), расчетная точка в верхнем (б) и нижнем (в) слое земли R ( p , q , l ) k n ( R( p, q 2nh, l ) R( p, q 2nh, l )), Рис .1б n 1 (1 k ) k n ( R( p, q 2nh, l ) R( p, q 2nh, l ) ) , Рис .1в n 0 Rij (1 k ) k n R( p, q 2nh, l ), Рис . 2б n 0 2 n R( p, q, l ) k R( p, q 2h, l ) (1 k ) k R( p, q 2nh, l ), Рис . 2в n 0 • Векторная форма записи • Ускорение сходимости бесконечных рядов методом выделения на основе мажоранты рядов S k n n ln(1 k ), k 1 n 1 Вывод: Эффективная расчетная модель, но только 2 слоя 3 МНОГОСЛОЙНАЯ 1D-МОДЕЛЬ ЗЕМЛИ Метод оптической аналогии. Модель разработана В.В. Бургсдорфом, улучшена С.В. Нестеровым. • • • Рекуррентные формулы для зеркальных изображений Огромное число отражений при резком различии удельных сопротивлений слоев Отсутствие средств ускорения сходимости Вывод: Трудоемкая модель. Задача повышения ее производительности ждет решения 4 3D-МОДЕЛЬ ЗЕМЛИ ИДЕЯ 1. Метод интегральных уравнений. Влияние границ раздела сред выражается в виде матрицы вносимого сопротивления заземлителя ΔR, определяемой J ( P) dG( P, Q) k J (Q) dS Q 0 2 dn S 1 I 2 D 22 D12 I 1 M dR pi i 1 dn M N dR pj j M 1 dn Ii Ij Ip 2kS p 0 D12I1 D22I 2 0 1 R11I1 R12 I 2 (R11 R12 D 221 D12 )I1 (R11 R)I1 1 R R 12 D 22 D12 Алгоритм исследован аналитически: быстрое затухание влияния соседних ячеек (1/r4) R N N i N j N R12 (i, j ) R12 (i, j ) D21 (i, j ) 1k m N D22 (i, j ) 4a 2 i N N 1 j N (i j m 2 ) 2 2 2 1 1 1 m , D21 (i, j ) , D22 (i, j ) 1 / 2ka2 2 2 2 2 3 2 2 2 2 4a i j m 4a (i j m ) ИДЕЯ 2. Метод интегральных уравнений совместно с методом зеркальных изображений. Вторичные токи на криволинейных границах отображаются от прямолинейных, что обеспечивает эффективность расчета. Вывод: Перспективная модель 5 МЕТОДЫ РАСЧЕТА ЗУ ПРИ ИМПУЛЬСНЫХ ВОЗДЕЙСТВИЯХ 1. Частотный метод. Трудоемкий, неточный. Применение нецелесообразно. 2. МЕТОД ДИСКРЕТНЫЙ СХЕМ. Шаговые алгоритмы Схемы индуктивности (а) и емкости (б) на n- шаге Тестовая задача. Найти входное напряжение при входном токе J(t)=t Формула Эйлера: R=L/h, G=C/h, En=Rin , Jn=Gun Формула трапеций R=2L/h, G=2C/h, En=Rin+un, Jn=Gun+in Операторный метод R=sL, G=sC, En=Lin , Jn=Cun s (2 2 j ) / h, f (t ) Re( (5 2 j 2) F ( s ) ) / h u E ( h) h 11 h 1 0,251 2h h ... 2 1 h 1 2h u T ( h) h 1 2 h 1 h2 0,51 h h ... 22 h 1 h 2 u 3 ( h) (2 2 j ) h 1 1 Re (5 2 j 2) h (2 2 j ) 2 h 2 ((2 2 j ) h 2) 2h 3 h 2 h3 0,251 2h h ... , 2 3 3 4h 2h 2 Вывод: Метод дискретных схем с шаговыми алгоритмами 1,3 порядка – эффективный метод расчета переходных процессов 6 МОДЕЛИ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ В ШАГОВЫХ АЛГОРИТМАХ МЕТОДИКА. Параметры НЭ определяются в начале шага и принимаются постоянными в течение шага 1. Нелинейность G. Искрообразование в 3. Нелинейность С. Емкость короны на земле по модели Е.Я. Рябковой: изменение радиуса стержня проводах ВЛ по данным кафедры ЭиТВН СПбГПУ C (U ) / C 0.625(U / U н 1) 2 / 3 4. Нелинейность μ(H). Универсальная характеристика Л.Р. Неймана 2. Нелинейность R: ВАХ ОПН по справочным данным U (I ) A I ВСХ изоляции по РД 153-34.3-35.125-99 15 U (t ) 340 l 1 t 9.5 Вывод: Нелинейные элементы легко учесть в шаговых алгоритмах 7 ДИСКРЕТНАЯ МОДЕЛЬ ЧАСТОТНОГО СОПРОТИВЛЕНИЯ ПРОБЛЕМА. Внутреннее сопротивление стержней Z(jω), параметры земли ρ(ω), ε(ω) зависят от частоты. Расчеты импульсных процессов на эквивалентной частоте не точны. РЕШЕНИЕ: Сопротивлению Z(jω) соответствует дискретная модель на n-шаге Доказательство Переходное сопротивление z(t) Z(jω) →Z(s) →z(t)=L–1[Z(s)/s] Подставляя z(t) в интеграл Дюамеля: Пример. Учет поверхностного эффекта стального стержня l s / Z ( s) 2a t u (t ) z (t )i(0) z (t x) i ( x) dx, i(0) 0 0 im1 im h m 1 n u n 1 Rk t m 1 n tm m 1 z(t n1 x) dx (im1 im ) Rnm1 R1 Rn l / ( n n 1) a h 1 k h z ( y ) dy, k 1..N h ( k 1) h un 1 R1 in 1 n ( Rn m1 Rn m 2 ) im R1 in 1 En l / a h En n ( Rnm1 Rnm2 ) im m2 m2 Вывод: Дискретная модель – эффективный способ учета сопротивлений Z(jω) в шаговых алгоритмах 8 СЕТОЧНЫЕ МОДЕЛИ ЭЛЕКТРОМАГНИТНЫХ ЭКРАНОВ Проблема. Сеточная модель не учитывает затухание волны в сплошном экране Допущение. Стальной экран идеальный (проникновение ЭМП только через отверстия), емкостью пренебрегаем. Магнитостатическая задача с г.у. H2=0. Метод интегральных уравнений с дискретизацией стержнями. Формулы, аналогичные c 3D-моделью земли Пример. Кубический экран Вывод: Сеточные модели электромагнитных экранов позволяет проводить их расчеты совместно с ЗУ 9 МОДЕЛИ ДЛЯ РАСЧЕТА КОНДУКТИВНЫХ ПОМЕХ 1. Коэффициенты экранирования: k=const – неточны, трудно обобщить 2. Передаточное сопротивление Zτ Напряжение помехи U= RI+jω(L-M)I=Zτ∙I идеальный экран L=M U= RI Для снижения помехи следует уменьшить ток экрана (ШУП, ЗУ, прокладка) 3. Сеточная модель экрана контрольного кабеля Вывод: Идеальный экран с передаточным сопротивлением R – простая и адекватная модель кабеля с двусторонним заземлением .Сеточная модель экрана универсальна. 10 ЗАКЛЮЧЕНИЕ. Рассмотрен комплекс моделей и методов, позволяющих проводить расчеты заземляющих устройств в задачах молниезащиты и ЭМС Спасибо за внимание