R 1

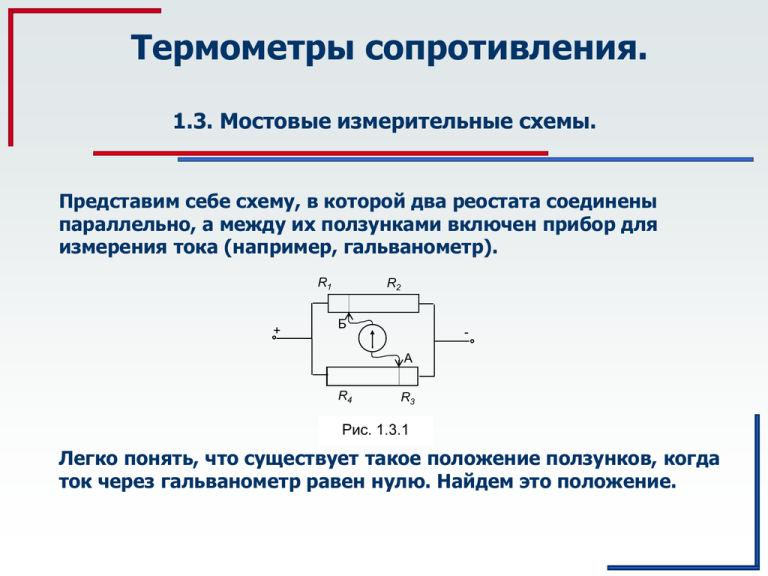
Термометры сопротивления.
1.3. Мостовые измерительные схемы.
Представим себе схему, в которой два реостата соединены
параллельно, а между их ползунками включен прибор для
измерения тока (например, гальванометр).
R1
+
R2
Б
А
R4
R3
Рис. 1.3.1
Легко понять, что существует такое положение ползунков, когда
ток через гальванометр равен нулю. Найдем это положение.
1.3. Мостовые измерительные схемы.
Изобразим ту же схему подругому (рис.1.3.2)
Б
R1
R2
i1
В
Г
i2
R4
R3
A
Рис. 1.3.2. Мостовая
измерительная схема.
Резисторы R1 , R2 , R3 и R4
называются плечами моста.
АБ – измерительная диагональ
ВГ – диагональ питания
Поскольку ток через гальванометр
равен нулю, то ток через резистор
R1 равен току через резистор R2 , а
ток через резистор R4 равен току
через резистор R3 . Обозначим эти
токи i1и i2 .
Условием равенства потенциалов
точек А и Б является условие
равенства падений напряжения на
сопротивлениях R1 и R4 :
а также на R2 и R3 :
i1  R1  i2  R4
i1  R2  i2  R3
1.3. Мостовые измерительные схемы.
Б
R1
R2
i1
В
Г
Перемножим левую часть первого уравнения
на правую часть второго, а правую часть
первого уравнения на левую часть второго.
i2
R4
Получим:
R3
A
i1  R1  i2  R4
i1  R2  i2  R3
После сокращения получим:
R1  R3  R2  R4
В уравновешенной мостовой схеме произведения
противоположных плеч равны друг другу.
(1.3.1)
1.3. Мостовые измерительные схемы.
Если же условие (1.3.1) не выполняется и
в измерительной диагонали течет ток, то
такая схема называется
неуравновешенной.
Б
R1
R2
В
Г
R4
R3
A
Покажем, что ток в измерительной
диагонали зависит от величины
неизвестного сопротивления R1. Для этого
воспользуемся теоремой об эквивалентном
генераторе:
i
U AБ
RКЗ  Rg
(1.3.2)
UАБ - разность потенциалов между точками А и Б при условии
отсутствия гальванометра,
Rg - внутреннее сопротивление гальванометра,
Rкз - сопротивление "короткого замыкания", т.е. сопротивление
между точками А и Б в случае отсутствия источника питания,
гальванометра и замыкания диагонали питания ВГ.
1.3. Мостовые измерительные схемы.
Б
R1
В
Согласно закону Ома:
Г
R4
U AБ  U A  U Б
Найдем UАБ как разность:
R2
U
R3
A
Из подобных
треугольников –
большого и малого найдем UА:
R3
UA

U
R4  R3

Рассуждая так же для
верхней ветки, найдем UБ:
U
UA 
U  R3
R4  R3
UБ 
U  R2
R1  R2
UA
R
В
R4
А
Рис.1.3.3
R3
Г
1.3. Мостовые измерительные схемы.
UA 
Б
R1
R2
В
Тогда получим:
Г
R4
R3
A
U  R3
R4  R3
UB 
 R3
R2 
 
U АБ  U 

 R4  R3 R1  R2 
 R1  R3  R2  R4 

 U 
 R1  R2 R4  R3  
Примем R2 = R3 = R4 = R. Кроме того: R1 ~ R. Тогда:
U АБ
U  R2
R1  R2
 R1  R  R 2 
R R
R R
  UR 1 2  U 1
 U 
4R
4R
 R  R R  R  
1.3. Мостовые измерительные схемы.
Для нахождения RКЗ перестроим схему с учетом «короткого
замыкания» (Рис. 1.3.4)
Тогда:
Б
R1
Б
R2
В
Г
R1
R2
B
R4
Г
RКЗ 
R R
R1  R2
 3 4
R1  R2 R4  R3
R3
R4
R3
A
А
Рис. 1.3.4
С учетом принятых
условий:
R2 R2
RКЗ 

R
2R 2R
1.3. Мостовые измерительные схемы.
Теперь подставим то, что мы нашли, в формулу (1.3.2):
i
U АБ
R1  R
U
RКЗ  Rg
4  RRg  R 
(1.3.3)
Значит, используя уравновешенную мостовую схему,
можно рассчитать неизвестное сопротивление R1 по
формуле (1.3.1), если известны сопротивления трех
других плеч.
Используя неуравновешенную мостовую схему, можно
рассчитать неизвестное сопротивление R1 по формуле
(1.3.3), если измерить ток в измерительной диагонали.