8216

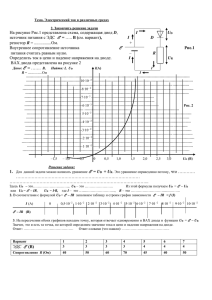
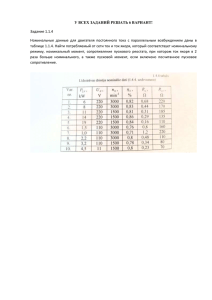
8216. Электрическая цепь, изображенная на рисунке, состоит из двух
диодов, шести одинаковых резисторов и источника тока, внутренним
сопротивлением которого можно пренебречь. Во сколько раз к
изменится ток через источник, если подключить его к точкам A и B с
другой полярностью? Диоды считать идеальными.
Решение. При исходном подключении источника потенциал точки A выше
потенциала точки C, в которой соединены два верхних резистора. В этом случае к
левому диоду приложено запирающее напряжение, поэтому ток через него не течет.
Эквивалентная схема в этом случае имеет вид, изображенный на рисунке (а).
Пусть
𝐼𝐶𝐿 = 𝐼,
Тогда
𝐼𝐾𝐹 = 𝐼, 𝐼𝑁𝐾 = 2𝐼.
Разность потенциалов
𝑈𝑁𝑀 = 2𝐼𝑅 + 𝐼𝑅 = 3𝐼𝑅.
Сила тока
𝐼𝑁𝑀 =
𝑈𝑁𝑀 3𝐼𝑅
=
= 3𝐼.
𝑅
𝑅
Тогда
𝐼𝐴𝑁 = 𝐼𝑁𝐾 + 𝐼𝑁𝑀 = 5𝐼.
ℰ = 5𝐼𝑅 + 3𝐼𝑅 = 8𝐼𝑅
Сопротивление
8𝐼𝑅 8
= ∙ 𝑅,
5𝐼
5
где R - сопротивление отдельного резистора.
При подключении источника с обратной полярностью потенциал точки В будет
выше потенциала точки С, поэтому ток не будет течь через правый диод, и
эквивалентная схема примет вид, изображенный на рисунке (б). В этом случае, в силу
𝑅𝐼 =
симметрии схемы разность потенциалов между точками N и K(C) равна нулю,
поэтому ток через центральный резистор не течет, и сопротивление всей цепи равно
ℰ = 𝑈𝐴𝐵 = 𝐼𝑅 + 𝐼𝑅 = 2𝐼𝑅
Сопротивление
2𝐼𝑅
𝑅𝐼𝐼 =
= 𝑅.
2𝐼
Поскольку напряжение на клеммах источника постоянно, искомое отношение
токов через источник
8
∙𝑅
𝑅𝐼
𝑘=
=5
= 1.6.
𝑅𝐼𝐼
𝑅
Ответ. 8/5=1,6