1.5 Формулы численного интегрирования
реклама

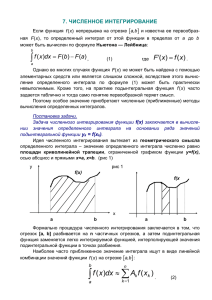
- 30 <== Возврат к содержанию раздела 1.5 Формулы численного интегрирования Определение: Численное интегрирование – это приближенное вычисление определенных интегралов вида b I f ( x) dx. (1.22) a Этот способ вычисления интегралов применяется, когда первообразную функции f (x) определить сложно или невозможно (например, f (x) задана таблицей значений). Постановка задачи: Вычислить интеграл (1.22) с заданной степенью точности по значениям подынтегральной функции f (x) в некоторых точках y отрезка [a;b] оси х. Определение: Упомянутые y = f (x) точки отрезка [a;b] называют узлами, а проходящие через них перпендиI куляры к оси х - ординатами. Общая схема численного интегрирования. Если значения a и b b a конечны, а функция f (x) непрерывна . . . xn-1 x n x на отрезке [a;b] , то интеграл I есть x0 x1 x2 площадь плоской фигуры, ограниРисунок 1.8 Схема численного интегрирования ченной кривой y=f (x), осью х и ординатами x=a, x=b. Приближенное вычисление интеграла сводится к разбиению отрезка [a;b] на множество более мелких отрезков, приближенному определению площади каждой получившейся криволинейной трапеции и их суммированию (рисунок 1.8). Определение: В литературе численное определение интеграла вида (1.22) называют квадратурой, а формулы численного интегрирования – квадратурными. Имеется две разновидности квадратурных формул. Первая предусматривает разбиение отрезка [a;b] на равные микроотрезки [xi-1;xi], i=1,2,...,n (x0=a, xn=b) длиной h=(b-a)/n . Наиболее популярные формулы этой разновидности – формулы прямоугольников, трапеций и Симпсона. Формулы второй разновидности основаны на определении положения точек хi, i=1,2,...,n-1 внутри отрезка [a;b], позволяющего достичь максимальной точности вычисления интеграла при заданном числе точек. Из этой разновидности чаще всего применяется формула Гаусса. . . . . . . b n xi a i 1xi 1 При использовании формул первой группы I f ( x) dx f ( x) dx . xi Приближенные значения интегралов I i f ( x) dx , i=1,2,...,n определяются xi 1 - 31 путем замены подынтегральной функции f (x) элементарной функцией внутри всех отрезков [xi-1;xi]. Формула прямоугольников (рисунок 1.9). На каждом отрезке [xi-1;xi], i=1,2,...,n площадь под кривой y=f (x) принимается приближенно равной площади прямоугольника с основанием x x h и высотой f i 1 i , т.е. 2 x xi I i h f i 1 , i=1,2,...,n, а 2 n x x I h f i 1 i . (1.23) 2 i 1 Формула трапеций (рисунок 1.10). На отрезках [xi-1;xi], i=1,2,...,n площадь под кривой y=f (x) заменяется площадью трапеции с основанием h и высотами f (xi-1) и f (xi). Следовательh но I i f ( xi1 ) f ( xi ) , i=1,2…,n, т.е. 2 h n (1.24) I f ( xi1 ) f ( xi ) . Рисунок 1.10 Формула трапеций 2 i1 Формула Симпсона (рисунок 1.11). На отрезке [xi-1;xi], i=1,2,...,n кривая y=f (x) заменяется квадратичной параболой, график которой проходит через x x x x точки x i 1 , f ( x i 1 ), i 1 i , f i 1 i , x i , f ( x i ). По формуле Лагран2 2 жа уравнение этой параболы можно представить в виде ( x zi )( x xi ) P2 ( x) f ( xi1 ) ( xi1 zi )( xi1 xi ) ( x xi1 )( x xi ) f ( zi ) ( zi xi1 )( zi xi ) ( x xi1 )( x zi ) f ( xi ) , ( xi xi1 )( xi zi ) Рисунок 1.11 Формула Симпсона где zi=(xi-1+xi)/2. Учитывая, что xi–xi-1=h, а zi–xi-1=xi–zi=h/2, запишем f ( xi1 ) xi f ( zi ) x i I i 2 ( x z )( x x ) dx 4 ( x xi1 )( x xi ) dx i i h 2 xi1 h 2 xi 1 Рисунок 1.9 Формула прямоугольников 2 f ( xi ) xi ( x xi1 )( x zi ) dx , i=1,2,...,n. h 2 xi 1 - 32 - h Взяв все три интеграла по частям, получим I i f ( xi1 ) 4 f ( zi ) f ( xi ) , 6 i=1,2,...,n, следовательно h n x x (1.25) I f ( xi 1 ) 4 f i 1 i f ( xi ) . 6 i 1 2 Формулу Симпсона называют иногда формулой парабол. Заменяя f (x) на отрезках [xi-1;xi], i=1,2,...,n полиномами 3-го, 4-го и т.д. порядков можно получить более сложные квадратурные формулы, носящие общее название: формулы Ньютона-Котеса. 4 Пример. Определить значение интеграла x3 3 x 2 2 dx при n=3. 1 Точное значение 4 4 1 1 4 x 4 4 x 3 2 x 1 255 4 63 6 6.75 ; формула прямоугольников I f (1.5) f (2.5) f (3.5) 11 8 9 8 65 8 5.625 ; 1 0222218 9 ; формула трапеций I f (1) f (2) f (2) f (3) f (3) f (4) 2 2 формула Симпсона 1 I f (1) 4 f (1.5) f (2) f (2 ) 4 f (2.5) f (3) f (3) 4 f (3.5) f (4) 6 0 44 8 2 2 36 8 2 2 260 8 18 6.75 . 6 Формула Симпсона дает абсолютно точный результат при интегрировании не только квадратичных, но и кубических полиномов для любого числа n. Эта формула соединяет в себе достоинства простоты и высокой точности. Для более простых формул прямоугольников и трапеций характерна гораздо меньшая точность. Ошибки вычисления интеграла (1.22) при фиксированном числе микроотрезков и можно вычислить по формулам : Op b a 3 f II (c), О (b a) 3 f II (c), О (b a) 5 f IV (c), 24 n 2 t 12 n 2 s 180 n 4 a c b (1.26) Из этих формул видно, что при одинаковом числе n формула прямоугольников вдвое точнее формулы трапеций, а формула Симпсона точнее обеих на порядок. Применять формулы (1.26) в вычислительной практике неудобно из-за необходимости вычисления производных функции f (x). Основой алгоритма вычисления интегралов вида (1.22) по формулам (1.23)-(1.25) является прием последовательного удвоения числа микроотрезков n и сравнения получаемых значений интеграла. Согласно формулам (1.26), удвоение числа n приводит к уменьшению Оp и Оt в 4 раза , а Оs - в 16 раз. Начальное число n обычно равно 10-20. Процесс удвоения n и пересчета значения интеграла заканчивают при выполнении неравенства: I ( n) I ( 2n) K F , где - заданная точность (обычно 10-410-5), KF - коэф- - 33 фициент, зависящий от используемой формулы (Kp=Kt=3, Ks=16). Увеличивать точность не имеет смысла, т.к. с ростом n и уменьшением ошибки ограничения увеличивается ошибка округления (при n >700 для формул прямоугольников и трапеций, n >100 для формулы Симпсона общая ошибка начинает увеличиваться). Квадратурная формула Гаусса. Основной принцип квадратурных формул второй разновидности виден из рисунка 1.12: необходимо так разместить точки х0 и х1 внутри отрезка [a;b], чтобы площади "треугольников" в сумме были равны площади "сегмента". При использовании формулы Гаусса исходный отрезок [a;b] сводится к отрезку [-1;1] заменой переРисунок 1.12 Иллюстрация к формуле Гаусса менной х на 0.5∙(b – a)∙t + 0.5∙(b + a). b 1 ba ba ba Тогда I f ( x)dx (t )dt , где (t ) f t . 2 2 2 a 1 Такая замена возможна, если a и b конечны, а функция f (x) непрерывна на [a;b]. Формула Гаусса при n точках xi, i=0,1,..,n-1 внутри отрезка [a;b]: n1 I [ Ai (ti )] , (1.27) n0 где ti и Ai для различных n приводятся в справочниках. Например, при n=2 t0 1 3 , t1 1 3, A0=A1=1; при n=3: t0=t20.775, t1=0, A0=A20.555, A10.889. 2 Пример. Вычислить значение 1 x 4 dx по формуле Гаусса для n=2: (t ) 0 20 1 1 t 4 1 1 t 4 ; I 1 (1 1 2 2 3 )4 1 (1 1 3 )4 8.2216 , 2 Точное значение: x 0 x 5 5 2 32 5 8.4 . 0 Алгоритм вычисления интеграла (1.22) по формуле Гаусса предусматривает не удвоение числа микроотрезков, а увеличение числа ординат на 1 и сравнение полученных значений интеграла. Преимущество формулы Гаусса – высокая точность при сравнительно малом числе ординат. Недостатки: неудобна при расчетах вручную; необходимо держать в памяти ЭВМ значения ti, Ai для различных n. Вычисление несобственных интегралов. Интеграл I f ( x) dx , где a f (x) - непрерывна на [a; ), может быть вычислен по формулам (1.23)-(1.25), если он является сходящимся. Общая схема вычисления: b a) выбирается большое число b и вычисляется f ( x) dx с точностью a - 34 /2 (используется последовательное удвоение числа микроотрезков n); b б) значение b удваивается и вновь вычисляется f ( x) dx ; a в) если I b I 2b 2, то вновь выполняется п. б) ; иначе I 2b - значение искомого интеграла с точностью . <== Возврат к содержанию раздела