Лабараторная. Интегральное исчисление. Вариант 10

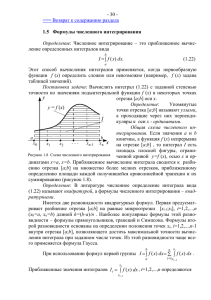
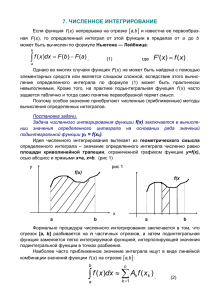
Лабораторная работа 2. Приближенное вычисление интегралов.
Цель работы: изучение различных методов вычисления определенных
интегралов, практическое интегрирование функций на ЭВМ.
Описание методов вычисления определенных интегралов.
Если функции u =  (x) и v =  (x) непрерывны на отрезке [a, b], а также
непрерывны на этом отрезке их производные, то справедлива формула
интегрирования по частям:
Существует огромное количество функций, интеграл от которых не
может быть выражен через элементарные функции. Для нахождения
интегралов
от подобных
функций
применяются разнообразные
приближенные методы, суть которых заключается в том, что
подынтегральная функция заменяется «близкой» к ней функцией, интеграл
от которой выражается через элементарные функции.
Формула прямоугольников.
Если известны значения функции f(x) в некоторых точках x0, x1, … , xm,
то в качестве функции «близкой» к f(x) можно взять многочлен Р(х) степени
не выше m, значения которого в выбранных точках равны значениям
функции f(x) в этих точках.
Если разбить отрезок интегрирования на n равных частей:
При этом y0 = f(x0), y1 = f(x1), …. , yn = f(xn).
Общая формула прямоугольников:
или
Формула трапеций является более точной по сравнению с формулой
прямоугольников.
1
Геометрически площадь криволинейной трапеции заменяется суммой
площадей вписанных трапеций. Очевидно, что чем больше взять точек n
разбиения интервала, тем с большей точностью будет вычислен интеграл.
Формула трапеций:
Формула парабол (формула Симпсона или квадратурная формула).
Томас Симпсон (1710-1761) - английский математик.
Разделим отрезок интегрирования [a, b] на четное число отрезков (2m).
Площадь криволинейной трапеции, ограниченной графиком функции f(x)
заменим на площадь криволинейной трапеции, ограниченной параболой
второй степени с осью симметрии, параллельной оси Оу и проходящей через
точки кривой, со значениями f(x0), f(x1), f(x2).
Для каждой пары отрезков построим такую параболу.
Уравнения этих парабол имеют вид Ax2 + Bx + C, где коэффициенты А,
В, С могут быть легко найдены по трем точкам пересечения параболы с
исходной кривой.
Обозначим
.
Если принять х0 = -h, x1 = 0, x2 = h, то
2
.
Тогда уравнения значений функции имеют вид:
C учетом этого:
Формула Симпсона:
Чем больше взять число m, тем более точное значение интеграла будет
получено.
Формула относительной погрешности:

I  Ih
*100% ,
I
I – точное значение интеграла, вычисленное через первообразную
функции; Ih – значение интеграла, полученное в результате применения
конкретной формулы интегрирования.
Блок-схема алгоритма программы интегрирования функции
(формула Симпсона).
При запуске программы требуется ввод подынтегральной функции;
первообразной функции; значений отрезка [a, b]; числа n – количество
подотрезков; значения точности, с которой необходимо вычислить значение
интеграла на отрезке [a, b].
Алгоритм нахождения значения интеграла
1
 arctg(x)
с заданной
0
точностью (10-5) по формуле Симпсона заключается в следующем:
1. Формула Симпсона для всего отрезка имеет вид Simp := (h/6)*(F(a) +
F(b) + Res), где переменная Res представляет собой сумму значений
функции F(x).
If Round(i/2) = i/2 then
Res := Res + 2*F(x) //четные
Else
Res := Res + 4*F(x); //нечетные.
2. Для нахождения величины шага, обеспечивающей заданную точность
организуем цикл, уменьшая шаг в 2 раза и находим значения интеграла
Int := (h/3)*(F(a) + F(b) + Res).
3
Алгоритм вычисление погрешности заключается в нахождении
первообразной функции Perv(a, b) и расчету по формуле, где переменная Int –
значение интеграла, вычисленное с помощью формулы Симпсона:
Prec := (Abs((Perv(a, b) - Int)/Perv(a,b)))*100.
Вариант 10.
Дано:
f(x) = arctg(x)
F(x) = x*arctg(x) – ln(1+x2)/2
a=0
b=1
Если n = 10 (количество подотрезков), то
1
Ответ:  arctg(x) = 0,43882, h = 0,025, δ = 0,0000012373.
0
4