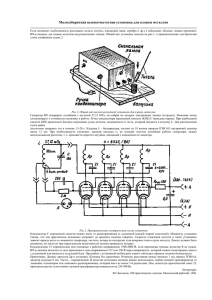
Установка и ход работы

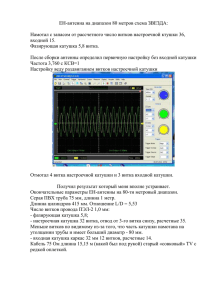
Смежные темы
Закон самоиндукции, закон Ленца, самоиндукция, соленоиды,
трансформатор, колебательный контур, резонанс, затухающие
колебания, логарифмический декремент, Q-фактор.
Принцип
Напряжение прямоугольного колебания низкой частоты
подается на колебательный контур, состоящий из катушек и
конденсаторов, генерирующих свободные, затухающие
колебания. Величины индукции рассчитываются на основе
измерянных собственных частот при известной емкости.
Оборудование
Экспериментальная установка Кобра 3
Источник питания 12 В/ 2 A
Информационный стандартный кабель RS 232
Программное обеспечение
для универсального самописца системы Кобра 3
Модуль функционального преобразователя
Системы Кобра 3
Индукционная катушка на 300 витков,
диаметром 40 мм
Индукционная катушка на 300 витков,
диаметром 32 мм
Индукционная катушка на 300 витков,
диаметром 25 мм
Индукционная катушка на 200 витков,
диаметром 40 мм
Индукционная катушка на 100 витков,
диаметром 40 мм
Индукционная катушка на 150 витков,
диаметром 25 мм
Рис. 1: Экспериментальная установка
12150.00 1
12151.99 2
14602.00 1
14504.61 1
Индукционная катушка на 75 витков,
диаметром 25 мм
Катушка на 1200 витков
Конденсатор на 470 нФ, 250 В, в корпусе 1
Коммуникационная коробка
Соединительный шнур, 250 мм, красный
Соединительный шнур, 250 мм, синий
Соединительный шнур, 500 мм, красный
Соединительный шнур, 500 мм, синий
ПК с системой Windows 95® или выше
11006.07
06515.01
39105.20
06030.23
07360.01
07360.04
07361.01
07361.04
1
1
1
1
1
1
2
2
Цель работы
Собрать колебательный контур, соединив катушки с
различными характеристиками (длиной, радиусом, количеством
витков) и конденсатор известной емкостью С. Используя
результаты
измерений
собственных
частот
рассчитать
индуктивности катушек и определить зависимость между:
1. индуктивностью и количеством витков
2. индуктивностью и длиной
3. индуктивностью и радиусом
12111.00 1
11006.01 1
11006.02 1
11006.03 1
11006.04 1
11006.05 1
11006.06 1
Установка и ход работы
Соберите экспериментальную установку как показано на Рис. 1.
Напряжение прямоугольного колебания низкой частоты (f ≈ 500
Гц) подается на катушку возбуждения L . Скачок в магнитном
поле приводит к появлению напряжения в катушке L1 и создает
свободное затухающее колебание в колебательном контуре L1C ,
частота которого измеряется при помощи интерфейса Кобра 3. В
эксперименте используются катушки с различной длиной l ,
диаметром 2r и количеством витков N (Таблица 1). Диаметр и
длина измеряются штангенциркулем и рулеткой, количество
витков задано в условии.
Рис.2: Установка для измерения индуктивности
Рис. 3: Параметры измерения
Таблица 1: Характеристики катушек
l , мм Код в каталоге
№ катушки
N
2r , мм
1
300
40
160
11006.01
2
300
32
160
11006.02
3
300
26
160
11006.03
4
200
40
105
11006.04
5
100
40
53
11006.05
6
150
26
160
11006.06
7
75
26
160
11006.07
Найдена зависимость между индуктивностью и радиусом,
длиной и количеством витков у катушек:
1.)
3, 6, 7 →
L
= f(N)
2.)
1, 4, 5 →
L/N2
= f(l)
3.)
1, 2, 3 →
L
= f(r)
Рис.4: Измерение периода колебаний
Зависимость между индуктивностью и количеством витков,
найденную для решения задачи 1, можно использовать при
решении задачи 2 (см. Цель работы).
Заметки
Расстояние между L1 и L 2 должно быть максимальным, чтобы
влиянием катушки возбуждения на частоте настройки можно было
пренебречь. Не располагайте металлические компоненты вблизи
катушек. Подсоедините экспериментальную установку Кобра 3 к
порту компьютера COM 1, COM 2 или USB (для подсоединения к
порту USB используйте преобразователь USB - RS232 14602.10).
Запустите программу для проведения измерений и выберите
Универсальный самописец системы Кобра 3. Начните измерение,
используя параметры, изображенные на Рис. 3. Для измерения
периода колебаний выберите «Survey Function» («Обзор») (см. Рис.
4).
На Рис. 4 изображен прямоугольный сигнал и затухающие
колебания после каждого пика.
Частоту f0 данного затухающего колебания можно определить:
f0 
1
T
Кобра 3, которое приводит к незначительному
(приблизительно 1 %) в резонансной частоте.
Следовательно, индуктивность можно рассчитать:
L
где T – период колебания.
Теория и расчет
Если ток силой I проходит через катушку (соленоид) длиной
l , поперечным сечением A  r 2 и количеством витков N ,
в катушке возникает магнитное поле. При l >>r магнитное
поле однородно, а его напряженность H рассчитывается:
H I
N
t
1
(7)
4 f 0 2 Cобщ
2
C общ  С  С в х и f 0 
где
0
2
В Таблице 2 представлены значения индуктивности катушек,
полученные при помощи выражения 5.
(1).
Магнитный поток рассчитывается:
Таблица 2
№ катушки
Ф      H  A
(2).
где μο –магнитная постоянная,
μ –магнитная проницаемость окружающей среды.
При изменении магнитного потока возникает напряжение на
концах катушки,

U инд   N  Ф
U инд
сдвигу
300
300
300
200
100
150
75
r, м
0,02
0,016
0,013
0,02
0,02
0,013
0,013
l, м
0,16
0,16
0,16
0,105
0,053
0,16
0,16
Lтеор , мкГн
794,65
537,75
375,91
484,38
202,22
93,48
23,37
В Таблице 3 представлены значения периода колебаний
и
соответствующие значения индуктивности катушек, полученные
при помощи выражения 7. Эти значения Lтеор изображены на
N 
  N      A   I
l

U инд   L  I
1
2
3
4
5
6
7
N
(3)
Рис. 5, 6 и 7.
Таблица 3
где
L       
N 2  r2
l
(4)
является
индуктивностью
катушки
(коэффициентом
самоиндукции).
Выражение (4) справедливо только в случае однородного
магнитного поля согласно (1) при l >>r.
Более точное значение индуктивности катушек при l >r
можно рассчитать по формуле:
r
L  2,110 6  N 2  r  ( )3 / 4
l
r
при 0   1
l
1
Tэксп , мкс
1
2
3
4
5
6
7
119,94
97,42
78,24
94,77
62,88
39,27
20,19
Lэксп , мкГн
776,09
512,01
330,25
448,53
213,31
83,20
21,99
Рис. 5: Зависимость индуктивности катушек при постоянной длине
и радиусе от количества витков.
(5)
В ходе выполнения эксперимента можно рассчитать
индуктивность катушек с различными характеристиками,
исходя из собственной частоты колебательного контура.
0 
№ катушки
(6)
LC общ
C общ – сумма известной емкости конденсатора и входной
емкости С в х (Кобра 3). Затухающий эффект достигается за
счет внутреннего сопротивления Rвнутр на входе установки
Рис.6: Зависимость индуктивности катушки на один виток от
длины при постоянном радиусе.
Рис. 7: Зависимость индуктивности катушки от радиуса при
постоянной длине и количестве витков.
Применив выражение
L  A N B
к значениям на Рис. 6, получаем
C  0,82  0,04 ; C теор = -0,75
к значениям на Рис. 5, получаем
B  1,95  0,04 ; Bтеор = 2 (см. Выражение 5)
2
Зная, что
L ~ N , можно получить
индуктивности катушки от ее длины.
Применив выражение
L
N
2
 Alc
зависимость
Применив выражение
L
 Ar D
N2
к значениям на Рис. 7, получаем
D  1,86  0,07 ; Dтеор  1,75
Таким образом, выражение 5 получено в рамках погрешности.