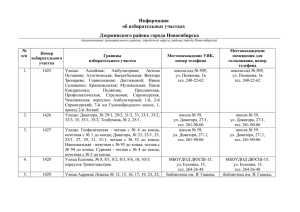
Урок математики Проломова С.К
реклама
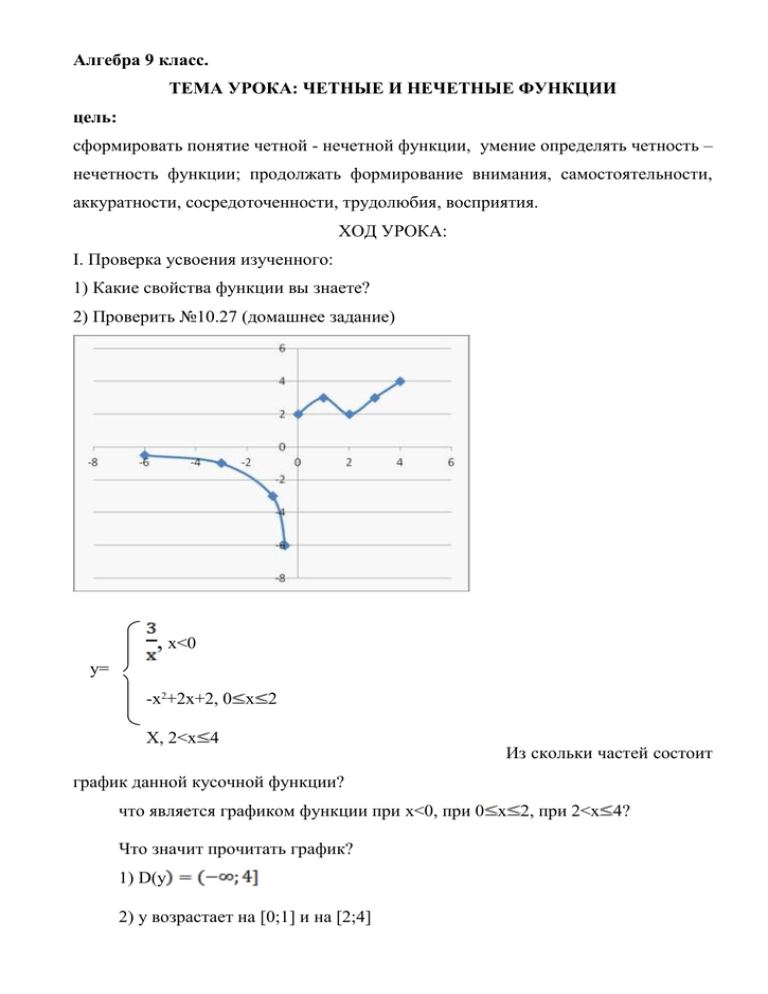
Алгебра 9 класс. ТЕМА УРОКА: ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ цель: сформировать понятие четной - нечетной функции, умение определять четность – нечетность функции; продолжать формирование внимания, самостоятельности, аккуратности, сосредоточенности, трудолюбия, восприятия. ХОД УРОКА: I. Проверка усвоения изученного: 1) Какие свойства функции вы знаете? 2) Проверить №10.27 (домашнее задание) , x<0 y= -x2+2x+2, 0 x 2 X, 2<x 4 Из скольки частей состоит график данной кусочной функции? что является графиком функции при x<0, при 0 x 2, при 2<x 4? Что значит прочитать график? 1) D(y 2) у возрастает на [0;1] и на [2;4] у убывает на [3) ограничена сверху; не ограничена сверху 4) у наиб. = 4; у наим. – не существует 5) непрерывна на открытом луче (-∞ и на отрезке [0;4] или терпит разрыв при х=0 6) выпукла вверх на отрезке [0; 2] 7) Е(у)=(∞[2;4] II/ Изучение нового материала Для чтения графиков используетсяте свойства функции, которые в той или иной степени нам были знакомы из курса алгебры 7-8 кл. Сегодня мы знакомимся с двумя новыми, очень важными свойствами функций 1) Опр1. Функцию у (x), xX называют четной, если для любого х из множества Х выполняется равенство (-х) = (х) Например, у = х2 – четная, так как у(-х) =(-х)2 = х2=у(х) Аналогично для у=х4, у=х6 Опр.2 Функцию у (x), xX называют нечетной, если для любого х из множества Х выполняется равенство (-х) = -(х) Пример, у=х3 (х) = х3; (-х) = (-х)3=-х3=-(х) значит у=х3 функция нечетная Аналогично для у=х, у=х5 и т.д. Сравнить показатели функций: Если показатель – четное число, то функция - четная; если нечетное, то функция нечетная 2) Определить четность – нечетность функции у = 2х+3 (x) = 2х+3 (-x) =2*(-х) +3= -2х+3≠ (x) (-x) =-2х+3= -(2х-3) ≠- (x) (x) ни четная, ни нечетная 3) Изучение вопроса о том, является «ли» функция четной или нечетной называют исследованием на четность. В опр.1 и опр.2 речь идет о х и –х. Это противоположные числа, функция существует и в точке х, и в точке –х, это значит, что –х принадлежит области определения функции одновременно с точкой х Если числовое множество Х вместе с каждым элементом х содержит и противоположный элемент –х, то Х называют симметричным множеством Например, (-2; 2), [-5; 5], (-∞;0) (0;+∞) – симметричные множества А (-2; 2]; (-2;3]; [-5;4] - несимметричные. Каким множеством должна быть область определения функции, чтобы функция была четной или нечетной? Если же D(f) – несимметричное множество, то f(x) ни четная, ни нечетная 4) Составить алгоритм исследования функции на четность Найти D(f) 1)Установить симметрично ли D(f) Да Нет 2) Составить f(-x) 3) Сравнить f(-x) и f(x) а) если f(-x) = f(х) хD(f), то четная б) если f(x) = -f(х) хD(f), то нечетная 5) Исследовать на четность функцию: №1 У=х4+ ; f (x) = х4+ Решение 1) D (f) = ∞∞ - симметричные множества 2) f(-x) = (-x)4+ = х4+ = f(x) f(x) - четная №2 y=f(x), f(x) = x5 - , x Решение 1) D (f) = ∞∞ - симметричные множества Ни четная Ни нечетная 2) F(-x) = (-x)5 - = -x5- = -x5+ = -(x5+ ) = - f(x) f(x) - нечетная №3 у=f(x), f(x) = Решение 1) x2-9 0 x2 9 x D (f) = ∞3(-3;3)3∞ - симметричные множества 2) f(-x) = f(x) – ни четная, ни нечетная №3 y=f(x), f(x)= Решение x-3 0 x 3 D(f) = [3;+∞ несимметричное множество F(x) – ни четная, ни нечетная функция 5) Геометрический смысл свойства четности и нечетности функции. Что значит х и –х - противоположные числа, а ординаты одинаковые. Как располагается эти точки на координатной плоскости? – Симметричны относительно ОУ 6) График нечетной функции симметричен относительно оси у f(-x) = - f(x) У точек с противоположными абсциссами и ординаты противоположные точки симметричны отностительно начало координат графике нечетной функции вывод о Верны ли обратные утверждения? III. Закрепление изученного: №11.1-11.2 (в,г) – устно №11.9-11.10 (в,г) – устно №11.5, 7 (в,г), 8 (в,г) IV. Домашнее задание §11 (определения, алгоритм) №1-4 (а,б), 7-10 (б,г)