Динамика пространства в глобальном времени
реклама

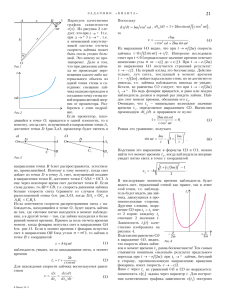
Äèíàìèêà ïðîñòðàíñòâà â ãëîáàëüíîì âðåìåíè ýôôåêòèâíàÿ àëüòåðíàòèâà îáùåé òåîðèè îòíîñèòåëüíîñòè Ä. Å. Áóðëàíêîâ 1) Íèæåãîðîäñêèé óíèâåðñèòåò èì. Í. È. Ëîáà÷åâñêîãî, 603900 Íèæíèé Íîâãîðîä, Ðîññèÿ Îäíàêî òàêîå ïåðåíåñåíèå ñïðàâåäëèâî äëÿ ñêàëÿðíîé âåëè÷èíû è (ïî ñëó÷àéíîìó ñîâïàäåíèþ) äëÿ ñàìîãî ïîëÿ ñêîðîñòåé. Çàãîòîâêó äëÿ ïåðåíîñà ïî âðåìåíè îò ëþáûõ òåíçîðîâ ïðè ïðîèçâîëüíîì èçìåíåíèè êîîðäèíàò ïî âðåìåíè ñîçäàë Ñîôóñ Ëè, ââåäÿ ïðè áåñêîíå÷íî ìàëîì ïðåîáðàçîâàíèè êîîðäèíàò x̄i = xi − ξ i (x) ò. íàç Ëè-âàðèàöèþ òåíçîðíîãî ïîëÿ (íàïðèìåð, êîâàðèàíòíîãî âåêòîðíîãî ïîëÿ Ai ): 1. ÄÈÍÀÌÈ×ÅÑÊÀß ÃÅÎÌÅÒÐÈß Îáùàÿ òåîðèÿ îòíîñèòåëüíîñòè (ÎÒÎ) [1, 2] ñòðîèòñÿ íà îñíîâå (ñòàòè÷åñêîé) ðèìàíîâîé ãåîìåòðèè ÷åòûðåõìåðíîãî ïðîñòðàíñòâà-âðåìåíè. Ðåøåíèÿ óðàâíåíèé Ýéíøòåéíà îïðåäåëÿþò âñå ÷åòûðåõìåðíîå ïðîñòðàíñòâî-âðåìÿ: ïðîøëîå, íàñòîÿùåå è áóäóùåå ñðàçó. Òåîðèÿ ãëîáàëüíîãî âðåìåíè (ÒÃÂ) îñíîâíûì ôèçè÷åñêèì îáúåêòîì ïîëàãàåò òðåõìåðíîå ïðîñòðàíñòâî, äèíàìè÷åñêè èçìåíÿþùååñÿ â îáùåì äëÿ âñåõ òî÷åê ïðîñòðàíñòâà ãëîáàëüíîì âðåìåíè, â êîòîðîì ñîâåðøàåòñÿ è ìèðîâàÿ äèíàìèêà. Ãåîìåòðèÿ ñî âðåìåí Äðåâíåé Ãðåöèè ñîçäàâàëàñü èç íàáëþäåíèÿ íàä âçàèìíûì ðàñïîëîæåíèåì ìàòåðèàëüíûõ òåë è èõ ïåðåìåùåíèÿìè, íå ñâÿçàííûìè ñî âðåìåíåì. È ãåîìåòðèÿ Åâêëèäà, è ãåîìåòðèÿ Ëîáà÷åâñêîãî, è ãåîìåòðèè Ãàóññà, Ðèìàíà íå âêëþ÷àþò â ñåáÿ ïîíÿòèå âðåìåíè. Ýòè ãåîìåòðèè ïðåäíàçíà÷åíû äëÿ ñïîêîéíî ñèäÿùèõ èëè ìåäëåííî ïðîãóëèâàþùèõñÿ ìóäðåöîâ, ïåðåä êîòîðûìè ðàñïîëîæåíû ÷åðòåæè èëè íåïîäâèæíûå ïðåäìåòû. Ìåõàíèêà Íüþòîíà âíåñëà â ìàòåìàòèêó îïèñàíèÿ ðåàëüíîñòè âðåìÿ. Îäíàêî Íüþòîí ñîâåðøåííî åñòåñòâåííî äëÿ ñâîåãî âðåìåíè ðàññìàòðèâàë ëèøü îäíîðîäíûå äâèæåíèÿ åâêëèäîâûõ ïðîñòðàíñòâ, Ïåðâîå îïèñàíèå äèíàìèêè ñ íåîäíîðîäíûì ïîëåì ñêîðîñòåé ïðèíàäëåæèò Ýéëåðó, êîãäà îí, ôîðìóëèðóÿ ñâîè çíàìåíèòûå óðàâíåíèÿ ãèäðîäèíàìèêè, ïðèìåíèë â ëîêàëüíîé ñèñòåìå êîîðäèíàò, ñâÿçàííîé ñ äâèæóùåéñÿ ÷àñòèöåé æèäêîñòè, âòîðîé çàêîí Íüþòîíà: ∂v 1 = − ∇p, ∂t ρ à çàòåì ïåðåíåñ ïðîèçâîäíóþ ïî âðåìåíè èç ñèñòåìû, â êîòîðîé ÷àñòèöà ïîêîèòñÿ (v = 0), â ëàáîðàòîðíóþ ñèñòåìó, çàìåíèâ ïðîèçâîäíóþ ïî âðåìåíè íà ò. íàç. δξ Ai = ξ s Ai ,s +ξ s ,i As .  äèíàìè÷åñêîé ãåîìåòðèè ïðîñòðàíñòâî ïðåäñòàâëÿåòñÿ ìíîæåñòâîì ñâîèõ òî÷åê è ñèñòåìà êîîðäèíàò, â êîòîðîé òî÷êè ñàìîãî ïðîñòðàíñòâà ñâîèõ êîîðäèíàò (x̄i ) íå ìåíÿþò, íàçîâàåòñÿ àáñîëþòíîé èíåðöèàëüíîé ñèñòåìîé. Òîãäà â íåêîòîðîé äðóãîé ñèñòåìå, ñâÿçü êîîðäèíàò òî÷åê ïðîñòðàíñòâà â êîòîðîé ñ êîîðäèíàòàìè â àáñîëþòíîé èíåðöèàëüíîé ñèñòåìå çàâèñèò îò âðåìåíè xi = f i (x̄, t), ñóùåñòâóåò ïîëå àáñîëþòíûõ ñêîðîñòåé ∂xi , (3) ∂t îòñóòñòâóþùåå â àáñîëþòíîé èíåðöèàëüíîé ñèñòåìå (÷òî è ÿâëÿåòñÿ åå ôîðìàëüíûì ïðèçíàêîì). Áåñêîíå÷íî ìàëîå ïðèðàùåíèå âðåìåíè dt ãåíåðèðóåò áåñêîíå÷íî ìàëóþ âàðèàöèþ êîîðäèíàò ξ i (x, t) = V i (x, t) dt, êîòîðîå ñ ó÷åòîì âàðèàöèè Ëè (2) ïðèâîäèò ïðîèçâîäíóþ ïî âðåìåíè òåíçîðíîãî ïîëÿ èç íåèíåðöèàëüíîé ñèñòåìû â èíåðöèàëüíóþ, îáðàçóÿ Vi = êîâàðèàíòíóþ ïðîèçâîäíóþ òåíçîðíîãî ïîëÿ ïî âðåìåíè ([3]). Îíà ñîäåðæèò r+2 ñëàãàåìûõ, ãäå r ðàíã òåíçîðà.  ÷àñòíîñòè, äëÿ ñêàëÿðíîãî ïîëÿ (r = 0) ∂f + V i ∂i f. ∂t Äëÿ êîâàðèàíòíîãî âåêòîðíîãî ïîëÿ Ai (x, t) Dt f (x, t) = ∂Ai + V s Ai ,s +V s ,i As . ∂t Îñîáî âàæíîé â äèíàìèêå ïðîñòðàíñòâà ÿâëÿåòñÿ êîâàðèàíòíàÿ ïðîèçâîäíàÿ ïî âðåìåíè îò ìåòðè÷åñêîãî òåíçîðà ïåðåíîñíóþ ïðîèçâîäíóþ ∂ ∂ → + (v · ∇). ∂t ∂t (2) Dt Ai = (1) Dt γij = 1) bur@phys.unn.runnet.ru 1 ∂γij + Vi;j + Vj;i . ∂t (4) 2 Ä. Å. Áóðëàíêîâ 2. ÒÅÎÐÈß ÃËÎÁÀËÜÍÎÃÎ ÂÐÅÌÅÍÈ Òåîðèÿ ãëîáàëüíîãî âðåìåíè èñõîäèò èç ñëåäóþùåé ôèçè÷åñêîé êîíöåïöèè ïðîñòðàíñòâà è âðåìåíè: ÿâëÿåòñÿ ìàòåðèàëüíûì íîñèòåëåì ãåîìåòðè÷åñêèõ ñâîéñòâ. Îíî òðåõìåðíî. Ïðîñòðàíñòâî ýòî ñîáñòâåííîå âðåìÿ ïðîñòðàíñòâà, åäèíîå äëÿ âñåõ åãî òî÷åê. Îíî âñþäó è âñåãäà òå÷åò îäèíàêîâî ðàâíîìåðíî, ñàìî ÿâëÿÿñü ìåðîé ðàâíîìåðíîñòè. Ãëîáàëüíîå âðåìÿ Ïðîñòðàíñòâî ÿâëÿåòñÿ íîñèòåëåì ãåîìåòðè÷åïîòîìó ÷òî ãåîìåòðè÷åñêèå ñâîéñòâà îïðåäåëÿþòñÿ ìåòðè÷åñêèì òåíçîðîì, øåñòü êîìïîíåíò êîòîðîãî ÿâëÿþòñÿ ãëàâíûìè ïîëåâûìè ïåðåìåííûìè ïðîñòðàíñòâà. Òåëà äâèæóòñÿ â ïðîñòðàíñòâå, äèíàìèêà ïîëåé (íàïðèìåð, ýëåêòðîìàãíèòíîãî) ñîâåðøàåòñÿ â ïðîñòðàíñòâå. Äëÿ êàæäîé äâèæóùåéñÿ òî÷êè îïðåäåëåíà àáñîëþòíàÿ ñêîðîñòü îòíîñèòåëüíî ïðîñòðàíñòâà. Îòíîñèòåëüíî ïðîñòðàíñòâà ñóùåñòâóåò àáñîëþòíîå äâèæåíèå, èëè, íàîáîðîò, â íåêîòîðîé ñèñòåìå êîîðäèíàò ñóùåñòâóåò ïîëå ñêîðîñòåé ïðîñòðàíñòâà. Òàêèì îáðàçîì äèíàìèêà ïðîñòðàíñòâà îïèñûâàåòñÿ øåñòüþ êîìïîíåíòàìè ïîëÿ ìåòðè÷åñêîãî òåíçîðà γij (x, t), îïðåäåëÿþùåãî åãî ãåîìåòðè÷åñêèå ñâîéñòâà â çàäàííûé ìîìåíò âðåìåíè, è òðåìÿ êîìïîíåíòàìè ïîëÿ àáñîëþòíûõ ñêîðîñòåé V i (x, t), îïðåäåëÿþùèìè, êàê êàæäàÿ òî÷êà ïðîñòðàíñòâà â êàæäûé äàííûé ìîìåíò äâèæåòñÿ îòíîñèòåëüíî âûáðàííîé ñèñòåìû êîîðäèíàò. Ïðîñòðàíñòâî ÿâëÿåòñÿ ìàòåðèàëüíûì íîñèòåëåì ãåîìåòðè÷åñêèõ ñâîéñòâ, ïîòîìó ÷òî óðàâíåíèÿ äèíàìèêè ìåòðè÷åñêîãî òåíçîðà è ïîëå ñêîðîñòåé ïîëó÷àþòñÿ èç ëàãðàíæåâûõ óðàâíåíèé è íàðÿäó ñ äðóãèìè ïîëÿìè (íàïðèìåð, ýëåêòðîìàãíèòíûì) îïðåäåëÿþò ýíåðãèþ. Óðàâíåíèÿ äèíàìèêè ìåòðèêè è ïîëå ñêîðîñòåé îïðåäåëÿþòñÿ èç âàðèàöèîííîãî ïðèíöèïà, ãäå ãðàâèòàöèîííîå äåéñòâèå ïðåäñòàâëÿåòñÿ êàê ðàçíîñòü êèíåòè÷åñêîé (êâàäðàòè÷íîé ïî ñêîðîñòÿì äåôîðìàöèè ìåòðèêè) è ïîòåíöèàëüíîé ýíåðãèé ïðîñòðàíñòâà (ïðîïîðöèîíàëüíîé ñêàëÿðíîé êðèâèçíå òðåõìåðíîãî ïðîñòðàíñòâà): ñêèõ ñâîéñòâ, c4 S= 16 π k Z (µij µji − (µjj )2 √ + R) γ d3 x dt + Sm , (5) ãäå Sm äåéñòâèå ïðî÷åé ìàòåðèè, à µij òåíçîð ñêîðîñòåé äåôîðìàöèè ïðîñòðàíñòâà, îáðàçîâàííûé èç êîâàðèàíòíûõ ïðîèçâîäíûõ ïî âðåìåíè ìåòðè÷åñêîãî òåíçîðà (4): 1 1 Dt γij = (γ̇ij + Vi;j + Vj;i ). (6) 2c 2c Ïîëå àáñîëþòíûõ ñêîðîñòåé V i âõîäèò â äåéñòâèå è ìîæåò âõîäèòü â íåãî òîëüêî ÷åðåç ýòîò òåíçîð. Âàðèàöèÿ äåéñòâèÿ ïî ìåòðè÷åñêîìó òåíçîðó γij ïðèâîäèò ê øåñòè äèíàìè÷åñêèì óðàâíåíèÿì, à ïî ïîëþ àáñîëþòíûõ ñêîðîñòåé ê òðåì óðàâíåíèÿì ñâÿçåé, òàê ÷òî ñèñòåìà óðàâíåíèé äèíàìèêè ïðîñòðàíñòâà äåâÿòü äèôôåðåíöèàëüíûõ óðàâíåíèé âòîðîãî ïîðÿäêà â ÷àñòíûõ ïðîèçâîäíûõ. Äåéñòâèå, êàê îáû÷íî â òåîðèè ïîëÿ, îïðåäåëÿåò ïëîòíîñòü ýíåðãèèR äèíàìè÷åñêîãî ïðîñòðàíñòâà è √ ãàìèëüòîíèàí Hγ = ρ γ d3 x: µij = c4 (µi µj − (µjj )2 − R). (7) 16 π k j i Âàæíîé åãî îñîáåííîñòüþ ÿâëÿåòñÿ çíàêîíåîïðåäåëåííîñòü. ρ= 2. ..1 Ñîáñòâåííîå âðåìÿ äâèæóùåãîñÿ íàáëþäàòåëÿ  ÎÒÎ, êàê ýòî ïîñòîÿííî ïîä÷åðêèâàë Ýéíøòåéí, ëîêàëüíî âûïîëíÿåòñÿ ñïåöèàëüíàÿ òåîðèÿ îòíîñèòåëüíîñòè: â ìàëîì ïðîñòðàíñòâî è âðåìÿ îïèñûâàþòñÿ ìåòðèêîé Ìèíêîâñêîãî (êàñàòåëüíîå ïðîñòðàíñòâî-âðåìÿ). Ãëîáàëüíàÿ êîíñòðóêöèÿ Òàíå íàêëàäûâàåò íèêàêèõ îãðàíè÷åíèé íà ëîêàëüíûå ñâîéñòâà. Ñïåöèàëüíàÿ òåîðèÿ îòíîñèòåëüíîñòè êàê ëîêàëüíàÿ ñòðóêòóðà ïðîñòðàíñòâà-âðåìåíè òàêæå åñòåñòâåííî âïèñûâàåòñÿ â ÒÃÂ. Äëÿ ëþáîãî äâèæóùåãîñÿ íàáëþäàòåëÿ ñîáñòâåííîå âðåìÿ îïðåäåëÿåòñÿ ÷åðåç ãëîáàëüíîå âðåìÿ è ñêîðîñòü îòíîñèòåëüíî ïðîñòðàíñòâà v i = ẋi − V i : r 1 dτ = dt 1 − 2 γij v i v j . (8) c Ýòî âûðàæåíèå ïðåäñòàâëÿåò ÷åòûðåõìåðíóþ ìåòðèêó, ëîêàëüíî ïðèâîäèìóþ ê ìåòðèêå Ìèíêîâñêîãî. Îñíîâíîé åå îñîáåííîñòüþ ÿâëÿåòñÿ g 00 = 1 âñþäó è âñåãäà. 3. ÎÁËÀÑÒÜ ÑÎÂÏÀÄÅÍÈß ÒÃÂ È ÎÒÎ 3. ..1 ÀÄÌ-ïðåäñòàâëåíèå Áëèçîñòü è ðàçëè÷èå Òàè ÎÒÎ ëåã÷å âñåãî ïðîñëåäèòü â ò. íàç. ÀÄÌ-ïðåäñòàâëåíèè ÎÒÎ. Àðíîâèòò, Äåçåð è Ìèçíåð [4] ïðåäñòàâèëè äåñÿòü êîìïîíåíò ÷åòûðåõìåðíîãî ìåòðè÷åñêîãî òåíçîðà ÷åðåç 3 Òåîðèÿ ãëîáàëüíîãî âðåìåíè øåñòü êîìïîíåíò ìåòðè÷åñêîãî òåíçîðà òðåõìåðíîãî ïðîñòðàíñòâà γij , òðåõìåðíûé âåêòîð V i (â îáîçíà÷åíèÿõ ÒÃÂ) è ôóíêöèþ õîäà âðåìåíè f (x, t): g00 = f 2 − γij V i V j ; gij = −γij . (9) g0i = γij V j ; Êîìïîíåíòû îáðàòíîãî ìåòðè÷åñêîãî òåíçîðà g 00 = 1 ; f2 i g 0i = V ; f2 i g ij = j V V − γ ij . f2 (10) Äåñÿòü óðàâíåíèé Ýéíøòåéíà ïîëó÷àþòñÿ êàê âàðèàöèîííûå óðàâíåíèÿ äëÿ äåñÿòè êîìïîíåíò ìåòðè÷åñêîãî òåíçîðà gαβ äåéñòâèÿ Ãèëüáåðòà Z c4 √ SG = R g d4 x, (11) 16π k ãäå R ñêàëÿðíàÿ êðèâèçíà ÷åòûðåõìåðíîãî ïðîñòðàíñòâà-âðåìåíè.  Òàêîìïîíåíòà g 00 = 1 (f = 1) âñåãäà è âåçäå. Ïðè ýòîì óñëîâèè äåéñòâèå Ãèëüáåðòà (11) ïåðåõîäèò â äåéñòâèå ïðîñòðàíñòâà (5). Êîìïîíåíòà g 00 íå ìîæåò âàðüèðîâàòüñÿ, è ôóíêöèÿ, êîòîðàÿ óìíîæàåòñÿ íà ýòó âàðèàöèþ, ìîæåò áûòü ïðîèçâîëüíîé. Ýòî è åñòü ïëîòíîñòü ýíåðãèè (7).  ÎÒÎ âàðüèðóþòñÿ âñå äåñÿòè êîìïîíåíò, ÷òî ïðèâîäèò ê äîïîëíèòåëüíîìó ïî ñðàâíåíèþ ñ äåâÿòüþ óðàâíåíèÿìè Òàóðàâíåíèþ ρ = 0. (12) Ïëîòíîñòü ïîëíîãî ãàìèëüòîíèàíà ïðîñòðàíñòâà è âåùåñòâà ðàâíà íóëþ, à ïîýòîìó ñàì ãàìèëüòîíèàí ðàâåí íóëþ. Ðåøåíèÿ ÎÒÎ, òàêèì îáðàçîì, îïðåäåëÿþò ïîäìíîæåñòâî âñåõ ðåøåíèé Òàñ ïëîòíîñòüþ ýíåðãèè âñþäó ðàâíîé íóëþ. Ýòî äåñÿòîå óðàâíåíèå â äîïîëíåíèå ê øåñòè äèíàìè÷åñêèì óðàâíåíèÿì è òðåì óðàâíåíèÿì ñâÿçè, âûðåçàþùåå â Òàñåêòîð ÎÒÎ. 3. ..2 Ïðèâåäåíèå ÎÒÎ ê ãëîáàëüíîìó âðåìåíè Êîñìîëîãè÷åñêèå ðåøåíèÿ ÎÒÎ âñåãäà èñõîäÿò èç ìåòðèêè â âèäå: âðåìåíí óþ êîîðäèíàòó τ = c t) òàê, ÷òîáû âûïîëíèëîñü óñëîâèå g 00 = 1. Ïî çàêîíàì ïðåîáðàçîâàíèÿ òåíçîðà ∂τ ∂τ (13) ḡ 00 = g αβ α β = 1. ∂x ∂x Íî ýòî äèôôåðåíöèàëüíîå óðàâíåíèå íà τ îêàçûâàåòñÿ óðàâíåíèåì Ãàìèëüòîíà ßêîáè äëÿ òðàåêòîðèé äâèæåíèÿ ñâîáîäíî ïàäàþùèõ ìàòåðèàëüíûõ òî÷åê (ëàáîðàòîðèé), îáùèì ñîáñòâåííûì âðåìåíåì êîòîðûõ è ÿâëÿåòñÿ t. Òàêèì îáðàçîì, â ãëîáàëüíîì âðåìåíè ðåàëèçóåòñÿ ôèçè÷åñêèé ïðèíöèï ýêâèâàëåíòíîñòè, ïðèâÿçûâàþùèé èíåðöèàëüíóþ ñèñòåìó ê ñâîáîäíî ïàäàþùåé ëàáîðàòîðèè, îäíàêî â îòëè÷èå îò ëèôòà Ýéíøòåéíà, ýòèõ ëàáîðàòîðèé ìíîæåñòâî è âðåìÿ â íèõ ñèíõðîíèçèðîâàíî. Òåì ñàìûì ïðèíöèï ýêâèâàëåíòíîñòè èç ëîêàëüíîãî ïðåâðàùàåòñÿ â ãëîáàëüíûé. Íî òðåõìåðíîå ìíîãîîáðàçèå, îáðàçîâàííîå ýòèìè òî÷êàìè-ëàáîðàòîðèÿìè, óæå íå ÿâëÿåòñÿ åâêëèäîâûì ïðîñòðàíñòâîì.  Òàäîêàçûâàåòñÿ òåîðåìà î òîì, ÷òî ëþáîå ñòàòè÷åñêîå ñôåðè÷åñêè ñèììåòðè÷íîå ðåøåíèå ñ ëþáûì âèäîì ìàòåðèè îáëàäàåò ïîëíîé ýíåðãèåé, ðàâíîé íóëþ [3]. Ïîýòîìó âñå òàêèå ðåøåíèÿ â Òàè ÎÒÎ âçàèìíî ïðèâîäèìû. Íàïðèìåð, ðåøåíèå Øâàðöøèëüäà â ãëîáàëüíîì âðåìåíè èìååò âèä 2 ds = 2M 1− r r 2 dt + 2 2M dt dr− r (14) (dr2 + r2 (dϑ2 + sin2 ϑ dϕ2 )). Ýòî âûðàæåíèå áûëî ïîëó÷åíî èç ìåòðèêè Øâàðöøèëüäà â 1921 ãîäó Ïýíëåâý [5], ïðîâîäèâøåì â ìåòðèêå Øâàðöøèëüäà ðàçëè÷íûå ïðåîáðàçîâàíèÿ t̃ = t + Φ(r) è ïîêàçàâøèì, ÷òî ñå÷åíèÿ t = const ðàçëè÷íû ïðè ðàçëè÷íîì âûáîðå ôóíêöèè Φ(r).  ÷àñòíîñòè, îí íàøåë ôóíêöèþ, ïðè êîòîðîé ïðîñòðàíñòâåííîå ñå÷åíèå ÿâëÿåòñÿ åâêëèäîâûì ïðîñòðàíñòâîì. Ýòî æå ðåøåíèå ïîëó÷àåòñÿ êàê ðåøåíèå óðàâíåíèé Òà[3]. Ðåøàÿ óðàâíåíèå (13) íåñëîæíî ïðèâåñòè ê ãëîáàëüíîìó âðåìåíè (g 00 = 1) è äðóãèå ðåøåíèÿ ÎÒÎ, íàïðèìåð, ìåòðèêó Íîðäñòðåìà èëè ìåòðèêó Êåððà. ds2 = c2 dt2 − γij (x, t) dxi dxj . Çäåñü êîìïîíåíòà ìåòðèêè g 00 = 1 âðåìÿ ãëîáàëüíîå, à g 0i = 0 ñèñòåìà ãëîáàëüíî èíåðöèàëüíàÿ. Ïðî÷èå (ãåîäåçè÷åñêè ïîëíûå) ðåøåíèÿ ÎÒÎ òàêæå ìîãóò áûòü ïðèâåäåíû ê ãëîáàëüíîìó âðåìåíè. Åñëè èìååòñÿ ÷åòûðåõìåðíàÿ ìåòðèêà gαβ â ïðîèçâîëüíûõ ÷åòûðåõìåðíûõ êîîðäèíàòàõ xα , äëÿ ïðèâåäåíèÿ åå ê ãëîáàëüíîìó âðåìåíè íóæíî ïðåîáðàçîâàòü êîîðäèíàòû (òî÷íåå âûáðàòü òîëüêî íîâóþ 4. ÎÒËÈ×Èß ÒàÎÒ ÎÒÎ Êàê áûëî ïîêàçàíî, ðåøåíèÿ ÎÒÎ îáðàçóþò ïîäìíîæåñòâî ðåøåíèé Òàñ ïëîòíîñòüþ ýíåðãèè ðàâíîé íóëþ. Ñíÿòèå ýòîãî îãðàíè÷åíèÿ ïðèâîäèò íå òîëüêî ê ïîÿâëåíèþ íîâûõ ðåøåíèé, íî è ê ñíÿòèþ ìíîãèõ ïðîáëåì ÎÒÎ, òàêèõ êàê ïðîáëåìà íà÷àëüíûõ äàííûõ, ïðîáëåìà êðèòè÷åñêîé ïëîòíîñòè, ãåî- 4 Ä. Å. Áóðëàíêîâ äåçè÷åñêîé ïîëíîòû, èëè âîçâðàòó ê òåîðèè Øðåäèíãåðà â êâàíòîâîé îáëàñòè. 4. ..1 Òàê êàê â ñèëó óðàâíåíèé äèíàìèêè ýíåðãèÿ ñîõðàíÿåòñÿ, ýòî åñòü äèôôåðåíöèàëüíîå óðàâíåíèå ïåðâîãî ïîðÿäêà, èìåþùåå ðåøåíèåì ôðèäìàíîâñêóþ öèêëîèäó: rm (1 − cos χ); 2 t= rm (χ − sin χ). 2 Ïðèíöèïèàëüíîå îòëè÷èå îò ðåøåíèÿ Ôðèäìàíà çäåñü ÷èñòî ôèçè÷åñêîå: â ýòîì ðåøåíèè îòñóòñòâóåò ïëîòíîñòü ìàòåðèè. Íàëè÷èå ïûëåâèäíîé ìàòåðèè ëèøü èçìåíÿåò êîíñòàíòó E . Òàêèì îáðàçîì â Òàîòñóòñòâóåò ïðîáëåìà êðèòè÷åñêîé ïëîòíîñòè â êîñìîëîãèè: Ìèð ìîæåò áûòü îòêðûòûì èëè çàìêíóòûì íåçàâèñèìî îò ïëîòíîñòè íàõîäÿùåéñÿ â íåì ìàòåðèè. 4. ..2 Êîñìè÷åñêàÿ äèíàìèêà Ñíÿòèå îãðàíè÷åíèÿ ÎÒÎ î ðàâåíñòâå íóëþ ïëîòíîñòè ýíåðãèè ïðèâîäèò ê ðåøåíèÿì, âàæíûì äëÿ êîñìè÷åñêîé äèíàìèêè: ïîëþ êîñìè÷åñêèõ âèõðåé [6]. Ýòè ðåøåíèÿ îáëàäàþò óäèâèòåëüíî ïðîñòûìè ìàòåìàòè÷åñêèìè ñâîéñòâàìè (ñëàáûé ïðèíöèï ñóïåðïîçèöèè) è îãðîìíûìè ýíåðãèÿìè. Âìåñòî ãèïîòåòè÷åñêèõ òåìíîé ìàòåðèè, òåìíîé ýíåðãèè, ãèãàíòñêèõ ÷åðíûõ äûð, ñ òî÷êè çðåíèÿ Òàãðîìàäíóþ ýíåðãåòè÷åñêóþ ðîëü â êîñìè÷åñêîé äèíàìèêå èãðàåò äèíàìè÷åñêàÿ ýíåðãèÿ ñàìîãî ïðîñòðàíñòâà.  ðàáîòå [6] ðàññìîòðåí øàð äèàìåòðîì 20 ñì., äåëàþùèé 1 îáîðîò â ñåêóíäó. Äëÿ âîâëå÷åíèÿ ïðîñòðàíñòâà âíå øàðà â êîãåðåíòíîå ñ íèì âðàùåíèå íóæíî çàòðàòèòü ýíåðãèþ, âûäåëÿåìóþ ïðè àííèãèëÿöèè 300 òûñÿ÷ òîíí âåùåñòâà. 4. ..3 i~ Êîñìîëîãè÷åñêèå ìîäåëè Äëÿ ôðèäìàíîâñêîé ìîäåëè ïðîñòðàíñòâà òðåõìåðíîé ñôåðû ïåðåìåííîãî ðàäèóñà r(t) ýíåðãèÿ (7) îòðèöàòåëüíà è ðàâíà (â ïëàíêîâñêîé ñèñòåìå åäèíèö): E = −3 r ṙ2 − 3 r. r= äðóãèõ ïîëåé, íàïðèìåð, êâàíòîâàÿ ýëåêòðîäèíàìèêà, ñòðîèòñÿ íà îñíîâå óðàâíåíèÿ Øðåäèíãåðà ∂Ψ = Ĥ Ψ, ∂t (15) îïðåäåëÿþùåãî äèíàìèêó âåêòîðà ñîñòîÿíèÿ ïðîñòðàíñòâà (è äðóãèõ ïîëåé) Ψ â ãëîáàëüíîì âðåìåíè. Ìåðà êâàíòîâûõ ôëóêòóàöèé ïðè ýòîì îïðåäåëÿåòñÿ íå â íåêîòîðîì ôèêñèðîâàííîì ïðîñòðàíñòâå, à ìåòðèêîé òîãî èñêðèâëåííîãî ïðîñòðàíñòâà, â êîòîðîì çàäàþòñÿ ýòè ôëóêòóàöèè. Òàêèì îáðàçîì, â îòëè÷èå, íàïðèìåð, îò êâàíòîâîé ýëåêòðîäèíàìèêè, ãäå îñíîâíîé ïðîáëåìîé (ïðè âçàèìîäåéñòâèè ñ ïîëåì ýëåêòðîíîâ) îêàçûâàåòñÿ íåëèíåéíîñòü, à ôóíêöèîíàëüíîå ïðîñòðàíñòâî ÿâëÿåòñÿ ïëîñêèì, â êâàíòîâîé ãðàâèòàöèè ñàìî ôóíêöèîíàëüíîå ïðîñòðàíñòâî îáëàäàåò êðèâèçíîé [7]. Êîìïîíåíòû ìåòðèêè γij êîììóòèðóþò äðóã ñ äðóãîì, òàêæå êàê è êîìïîíåíòû èìïóëüñîâ π kl , îäíàêî âûðàæåíèå äëÿ ãàìèëüòîíèàíà çíà÷èòåëüíî óïðîùàåòñÿ, åñëè ââåñòè àôèííûå èìïóëüñû, à èç íèõ âûäåëèì åùå øïóð πll , êîòîðûé êîììóòèðóåò (â ñìûñëå ñêîáîê Ïóàññîíà) ñ êàæäûì àôôèííûì èìïóëüñîì: πji = qji + δji π; 3 qii = 0; πii = π, (16) òî â ýòèõ ïåðåìåííûõ (è ïðè V i = 0) ãàìèëüòîíèàí (7) âûãëÿäèò ïðîùå: 1 H=√ γ 2 qji qij π2 − 3 √ − γ (3) R, 2 (17) ïðè÷åì ìåòðèêà âõîäèò â êèíåòè÷åñêóþ ýíåðãèþ √ òîëüêî ÷åðåç γ , à ýòà ïåðåìåííàÿ êîììóòèðóåò ñ qji , êîòîðûå, îäíàêî, äðóã ñ äðóãîì íå êîììóòèðóþò: 1 qji (x), qlk (x0 ) = (δli qjk − δjk qli )δ(x − x0 ). 2 (18) Ýòî êîììóòàöèîííûå ñîîòíîøåíèÿ òîêîâ ãðóïïû Sl(3), êîòîðûå òàêèì îáðàçîì åñòåñòâåííî âîçíèêàþò â äèíàìè÷åñêîé òåîðèè ãðàâèòàöèè. Ýòè îñëîæíåíèÿ ñâÿçàíû ñ ôîíîâîé íåçàâèñèìîñòüþ (background independence) êâàíòîâîé ãðàâèòàöèè. Êâàíòîâàÿ òåîðèÿ ãðàâèòàöèè Íî êîíå÷íî, íàèáîëåå ñèëüíîå èçìåíåíèå ïðåòåðïåâàåò êâàíòîâàÿ òåîðèÿ ãðàâèòàöèè. Ñíèìàåòñÿ êàòàñòðîôè÷åñêîå ñîîòíîøåíèå ÎÒÎ H = 0, îñòàíàâëèâàþùåå âñþ êâàíòîâóþ äèíàìèêó.  Òàêâàíòîâàÿ òåîðèÿ ãðàâèòàöèè, êàê è êâàíòîâàÿ òåîðèÿ 4. ..4 Êâàíòîâàÿ êîñìîëîãèÿ  êà÷åñòâå ïðîáíîãî êàìíÿ â òîì èëè èíîì ïîäõîäå ê êâàíòîâîé òåîðèè ãðàâèòàöèè (ïî÷òè) âñåãäà ðàññìàòðèâàþòñÿ êîñìîëîãè÷åñêèå çàäà÷è ñ êîíå÷íûì ÷èñëîì ñòåïåíåé ñâîáîäû. 5 Òåîðèÿ ãëîáàëüíîãî âðåìåíè Ðàññìîòðèì êîìïàêòíóþ êîñìîëîãè÷åñêóþ ìîäåëü ôðèäìàíîâñêîãî òèïà [8], îäíîðîäíóþ è èçîòðîïíóþ ñ ïðîñòðàíñòâîì â âèäå òðåõìåðíîé ñôåðû, çàïîëíåííîãî âåùåñòâîì ñ óðàâíåíèåì ñîñòîÿíèÿ ε = 3 p. Èç ãåîìåòðèè ïðîñòðàíñòâà ó÷èòûâàåòñÿ òîëüêî èçìåíåíèå ðàäèóñà r. Ãàìèëüòîíèàí H=− p2r + r2 q2 + , 2r 2r u0 + (−r2 + q 2 )u = 2 r E u. (20) r Âîïðîñ î ìåðå â ôóíêöèîíàëüíîì ïðîñòðàíñòâå òðåáóåò äîïîëíèòåëüíîãî èçó÷åíèÿ (âèäèìî, r5 èëè r2 ), íî òàê êàê ïîêà ìû ñòàâèì öåëü îïèñàíèÿ â ïðèíöèïå, óðàâíåíèå (20) çàïèñàíî ïðè ìåðå â ôóíêöèîíàëüíîì ïðîñòðàíñòâå åäèíèöà. Ñïåêòð ýòîãî óðàâíåíèÿ äèñêðåòåí. Ðåøåíèÿ ðàñïàäàþòñÿ íà äâà êëàññà ïî ïîâåäåíèþ â îêðåñòíîñòè íóëÿ: êàê r0 è êàê r2 . Äëÿ èçó÷åíèÿ êâàíòîâîé ïðîáëåìû Áîëüøîãî Âçðûâà ïðåäñòàâëÿåò èíòåðåñ ïåðâûé êëàññ, òàê êàê âî âòîðîì ïëîòíîñòü âåðîÿòíîñòè ïðè r → 0 âñåãäà ðàâíà íóëþ. Ñîáñòâåííûå çíà÷åíèÿ ýíåðãèè äëÿ ïåðâûõ âîñüìè òàêèõ ôóíêöèé ïðè q = 0 (ìàòåðèÿ îòñóòñòâóåò äèíàìèêà òîëüêî ïðîñòðàíñòâà) è q = 1 ïðèâåäåíû â òàáëèöå: u00 − q=0 q=1 1 -0.977722 4.42817 2 -3.05247446 -2.3182877 3 -4.16434141 -3.6338011 4 -5.03491431 -4.5990728 5 -5.77537028 -5.3970940 6 -6.43100378 -6.0924244 7 -7.02566164 -6.7165684 8 -7.57373725 -7.2876611 r (19) ãäå q 2 õàðàêòåðèçóåò ñîõðàíÿþùååñÿ êîëè÷åñòâî óëüòðàðåëÿòèâèñòñêîé ìàòåðèè. Âîëíîâàÿ ôóíêöèÿ ÿâëÿåòñÿ ôóíêöèåé âðåìåíè è ðàäèóñà ñôåðû r, ïåðåìåííûå ðàçäåëÿþòñÿ. Îáîçíà÷àÿ øòðèõîì ïðîèçâîäíóþ ïî ðàäèóñó, ñèììåòðèçóÿ p2 /r, ïîëó÷àåì ñòàöèîíàðíîå êîñìîëîãè÷åñêîå âîëíîâîå óðàâíåíèå (â ïëàíêîâñêîé ñèñòåìå åäèíèö): n u Ïðè q = 0 âñå ñîáñòâåííûå çíà÷åíèÿ ýíåðãèè îòðèöàòåëüíû, ïðè q ≥ 1 ïåðâûå ìîäû èìåþò ïîëîæèòåëüíóþ ýíåðãèþ. Ïåðâûå øåñòü (íåíîðìèðîâàííûõ) ôóíêöèé äëÿ ÷èñòîãî ïðîñòðàíñòâà (q = 0) ïðèâåäåíû íà ãðàôèêå: Âñëåäñòâèå íåíîðìèðîâàííîñòè ôóíêöèé è íåáîëüøîé èõ íåîðòîãîíàëüíîñòè çà ñ÷åò ïðèáëèæåííîãî èíòåãðèðîâàíèÿ â êîíå÷íûõ ïðåäåëàõ âû÷èñëÿåòñÿ ìåòðè÷åñêàÿ ìàòðèöà rZ max Mij = ui (r) uj (r) dr 0 è âû÷èñëåíèÿ ìàòðè÷íûõ îïåðàòîðîâ ïðîâîäèòñÿ ñ −1 îáðàòíîé ìàòðèöåé K ij = Mij . Äëÿ àíàëèçà äèíàìèêè ðàäèóñà èíòåðåñåí îïåðàòîð ðàäèóñà rji = n X K is s=1 rZ max r us (r) uj (r) dr. 0 Ïðè n = 8 ñîáñòâåííûå çíà÷åíèÿ ýòîé ìàòðèöû (ñîáñòâåííûå çíà÷åíèÿ îïåðàòîðà ðàäèóñà) ðàâíû (0.51, 1.7, 2.6, 3.4, 4.2, 5.0, 5.8, 6.8). Ñ óâåëè÷åíèåì n (÷èñëà ôóíêöèé) ìèíèìàëüíîå ñîáñòâåííîå çíà÷åíèå óìåíüøàåòñÿ, à ìàêñèìàëüíîå ðàñòåò, òàê ÷òî èõ ïðîèçâåäåíèå ïðèáëèçèòåëüíî îñòàåòñÿ ÷óòü áîëüøå π . Ïîýòîìó êâàíòîâûå ýôôåêòû íå ïðåäîòâðàùàþò Áîëüøîé Âçðûâ, à ñ ó÷åòîì òîãî, ÷òî ïîñòîÿííàÿ Ïëàíêà â ñèñòåìå åäèíèö Õåâèñàéäà èìååò ðàçìåðíîñòü êâàäðàòà äëèíû, ïðèâîäÿò ê ãèïîòåçå î íåêîòîðîì êîñìîëîãè÷åñêîì ñîîòíîøåíèè íåîïðåäåëåííîñòåé: Ïðîèçâåäåíèå ìàêñèìàëüíîãî è ìèíèìàëüíîãî ðàäèóñîâ Ìèðà íå ìåíüøå k ~/c3 . Íà ðèñóíêå ïðåäñòàâëåí âîëíîâîé ïàêåò â ïðîñòðàíñòâå n = 8, èìåþùèé ìèíèìàëüíîå ñîáñòâåííîå çíà÷åíèå ðàäèóñà r = 0.51. 1.2 1 0.8 0.6 0.4 0.2 2 -0.2 4 6 8 10 12 6 Ä. Å. Áóðëàíêîâ Îäíàêî ýòîò ïàêåò íå ÿâëÿåòñÿ ñòàöèîíàðíûì è íà÷èíàåò ðàcïëûâàòüñÿ. Ïðè ýòîì ðàñøèðåíèå íîñèò íå ìîíîòîííûé õàðàêòåð: ïàêåò (êâàäðàò ìîäóëÿ) ðàñïàäàåòñÿ íà äâå ñîñòàâëÿþùèå, îäíà èç êîòîðûõ óäàëÿåòñÿ îò íóëÿ, à âòîðàÿ îñöèëëèðóåò âáëèçè íóëÿ: r Ñ òî÷êè çðåíèÿ êâàíòîâîé ìåõàíèêè â êàêîé-ëèáî çàäà÷å, íàïðèìåð, òâåðäîãî òåëà ïîäîáíîå ïîâåäåíèå ïëîòíîñòè âåðîÿòíîñòè íå âûçâàëî áû ñåðüåçíûõ âîïðîñîâ. Îäíàêî ïðèìåíèòåëüíî ê Ðàäèóñó Ìèðà óíèêàëüíîé, åäèíñòâåííîé ïåðåìåííîé âîïðîñû âîçíèêàþò. Êàêîâ æå Ðàäèóñ Ìèðà äëÿ íàñ? Åñëè ñ êàêèì-òî ñðåäíèì çíà÷åíèåì è ìàëûìè ôëóêòóàöèÿìè âîêðóã íåãî êàê-òî ìîæíî ñìèðèòüñÿ, òî êàê òðàêòîâàòü îäíîâðåìåííóþ âåðîÿòíîñòü äâóõ ñóùåñòâåííî ðàçëè÷íûõ ðàäèóñîâ? ×òî áóäåò, åñëè èçìåðèòü Ðàäèóñ Ìèðà? Ïðîèçîéäåò ðåäóêöèÿ âîëíîâîãî ïàêåòà ëèáî â îáëàñòü áîëüøèõ, ëèáî â îáëàñòü ìàëûõ ðàäèóñîâ? Îòâåò ñîñòîèò â òîì, ÷òî Ðàäèóñ Ìèðà íåïîñðåäñòâåííî èçìåðèòü íåâîçìîæíî. Õýáë çàìåðèë åãî ïî ñâîéñòâàì ôîòîíîâ, èäóùèõ îò óäàëåííûõ ãàëàêòèê. Ýòè ôîòîíû òàêæå ïîä÷èíÿþòñÿ êâàíòîâîé òåîðèè è íà èõ êâàíòîâîå ïîâåäåíèå, äîñòóïíîå íàøåìó èçìåðåíèþ, ìîæåò âëèÿòü êàê îáëàñòü áîëüøèõ, òàê è ìàëûõ ðàäèóñîâ, íî ïðè ôèêñàöèè ôîòîíà íèêàêîé ðåäóêöèè âîëíîâîé ôóíêöèè Ðàäèóñà Ìèðà íå ïðîèñõîäèò (ñì. [9]). Ïîäàâëÿþùåå êîëè÷åñòâî êâàíòîâûõ ïåðåìåííûõ íèêåì íå íàáëþäàåòñÿ. Èõ êâàíòîâî-ìåõàíè÷åñêîå ïîâåäåíèå ïðîÿâëÿåòñÿ ëèøü ÷åðåç èõ âëèÿíèå íà ìàëîå ÷èñëî íàáëþäàåìûõ ïåðåìåííûõ. Ðàäèóñ Ìèðà ñ êâàíòîâî-ìåõàíè÷åñêîé òî÷êè çðåíèÿ ìîæåò èìåòü äîñòàòî÷íî ðàçìàçàííûå çíà÷åíèÿ, íî ýòî ìîæåò âûçâàòü ëèøü ñïåöèôèêó â íàáëþäàåìîì (èëè åùå íå íàáëþäàâøåìñÿ) ïîâåäåíèè íàáëþäàåìûõ îáúåêòîâ (ôîòîíîâ, êîñìè÷åñêèõ ÷àñòèö). Âèäèìî, êâàíòîâàÿ ôèçèêà â îñíîâå ñâîåé èìååò íå âîëíîâóþ ôóíêöèþ, à ìàòðèöó ïëîòíîñòè. 5. ÇÀÊËÞ×ÅÍÈÅ Ñòðîÿñü íà áîëåå ðàçâèòîì ìàòåìàòè÷åñêîì àïïàðàòå, Òàââîäèò â ôèçèêó (â îáùåì òî ñòàðûé, äàâ- íî èçâåñòíûé íà óðîâíå ôèëîñîôèè) íîâûé ôèçè÷åñêèé îáúåêò: ïðîñòðàíñòâî. Ñ òî÷êè çðåíèÿ òåîðåòè÷åñêîé ôèçèêè ýòî åñòü äåâÿòèêîìïîíåíòíîå ïîëå ñ èñêðèâëåííûì ôóíêöèîíàëüíûì ïðîñòðàíñòâîì. Êàê è äðóãèå ïîëÿ, íàïðèìåð, ýëåêòðîìàãíèòíîå, îíî îáëàäàåò ïëîòíîñòüþ è ïîòîêîì ýíåðãèè, ïðè÷åì â êîñìè÷åñêèõ ìàñøòàáàõ ýíåðãèÿ äåôîðìèðîâàííîãî ïðîñòðàíñòâà îãðîìíà âñëåäñòâèå îãðîìíîñòè ìíîæèòåëÿ c4 /(16 π k) â âûðàæåíèè äëÿ ïëîòíîñòè ýíåðãèè (7). Íàø ìèð ïî÷òè Åâêëèäîâ íå âñëåäñòâèå èäåàëüíîñòè åâêëèäîâîé ãåîìåòðèè, à âñëåäñòâèå òîãî, ÷òî îòêëîíåíèÿ îò åâêëèäîâîñòè òðåáóþò îãðîìíûõ çàòðàò ýíåðãèè. Èçó÷åíèå ñâîéñòâ ýòîãî ôèçè÷åñêîãî îáúåêòà, âîçìîæíî, ïðîëüåò ñâåò íà ñîâðåìåííûå ïðîáëåìû êîñìè÷åñêîé äèíàìèêè, îáúÿñíÿåìûå ñåé÷àñ òåìíîé ìàòåðèåé è ïîäîáíûìè ýêçîòè÷åñêèìè ñóùíîñòÿìè. Èçó÷åíèå êâàíòîâûõ ñâîéñòâ ïðîñòðàíñòâà, âîçìîæíî, ïðîäâèíåò íàñ è â ïîíèìàíèè êâàíòîâîé ñóùíîñòè Ìèðà. Ôèçèêà ïðîñòðàíñòâà äî ïîðû äî âðåìåíè íå ñâÿçàíà ñ ðåëÿòèâèçìîì è ìîæåò ñòðîèòüñÿ äî ñïåöèàëüíîé òåîðèè îòíîñèòåëüíîñòè. Ýòîò ïóòü ìîæíî ïðîéòè âñëåä çà Íèëüñîì Áüåðíîì (Niels Bj orn) [10], êîòîðûé õîòÿ è ÿâëÿåòñÿ âûìûøëåííîé ëè÷íîñòüþ, îäíàêî èìåííî ðàáîòà íàä åãî ñòàòüÿìè ïðèâåëà àâòîðà ê ÿñíîìó ïîíèìàíèþ äèíàìèêè ïðîñòðàíñòâà â ãëîáàëüíîì âðåìåíè. Èìåííî åìó ÿ âûðàæàþ ñâîþ áëàãîäàðíîñòü. Ñïèñîê ëèòåðàòóðû 1. Misner C.W., Thorne K., Wheeler J.A. Gravitation (San Francisco: Freeman, 1974). [Ïåðåâîä: Ìèçíåð ×., Òîðí Ê., Óèëåð Äæ. Ãðàâèòàöèÿ. Ì.:Ìèð, 1977]. 1. 2. Ëàíäàó Ë.Ä., Ëèôøèö Å.Ì. Òåîðèÿ ïîëÿ. Ì.: Íàóêà, 1988. 1. 3. Áóðëàíêîâ Ä. Å. Äèíàìèêà ïðîñòðàíñòâà (Íèæíèé Íîâãîðîä: Èçäàòåëüñòâî ÍÍÃÓ, 2005) 1. , 3. ..2, 3. ..2 4. Arnovitt R, Deser S, and Misner C. W. Phys. Rev. 116, 1322 (1959). 3. ..1 5. Painleve P. C.R. Acad. Sci. (Paris). 173, 677 (1921). 3. ..2 6. Burlankov D. E. arXiv: gr-qc/0406112 (2004). 4. ..2 7. Áóðëàíêîâ Ä.Å. ÆÝÒÔ, 51. 842 (1966). 4. ..3 8. Burlankov D. E. arXiv: gr-qc/0406110v1 (2004). 4. ..4 9. Áëóì Ê. Òåîðèÿ ìàòðèöû ïëîòíîñòè è åå ïðèëîæåíèÿ. Ì.: Ìèð, 1983. 4. ..4 10. Áóðëàíêîâ Ä. Å. ÓÔÍ 174, âûï. 8, 899 (2004). 5.