Задача № 1.
реклама
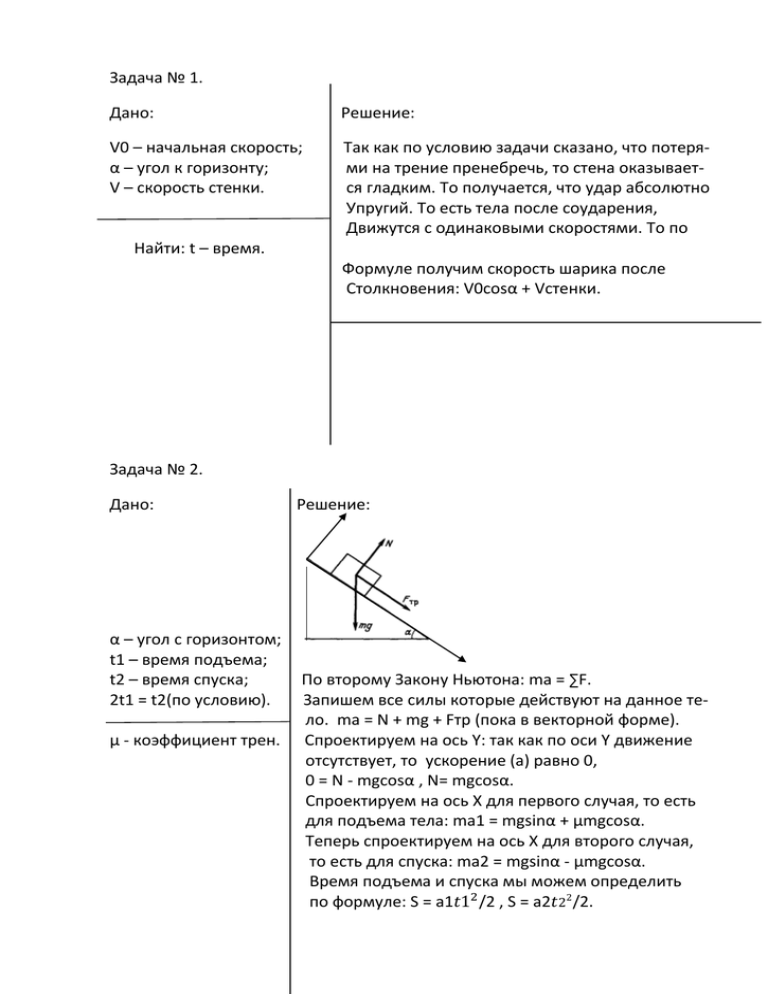
Задача № 1. Дано: Решение: V0 – начальная скорость; α – угол к горизонту; V – скорость стенки. Так как по условию задачи сказано, что потерями на трение пренебречь, то стена оказывается гладким. То получается, что удар абсолютно Упругий. То есть тела после соударения, Движутся с одинаковыми скоростями. То по Найти: t – время. Формуле получим скорость шарика после Столкновения: V0cosα + Vстенки. Задача № 2. Дано: α – угол с горизонтом; t1 – время подъема; t2 – время спуска; 2t1 = t2(по условию). µ - коэффициент трен. Решение: По второму Закону Ньютона: ma = ∑F. Запишем все силы которые действуют на данное тело. ma = N + mg + Fтр (пока в векторной форме). Спроектируем на ось Y: так как по оси Y движение отсутствует, то ускорение (а) равно 0, 0 = N - mgcosα , N= mgcosα. Спроектируем на ось X для первого случая, то есть для подъема тела: ma1 = mgsinα + µmgcosα. Теперь спроектируем на ось X для второго случая, то есть для спуска: ma2 = mgsinα - µmgcosα. Время подъема и спуска мы можем определить по формуле: S = a1𝑡12 /2 , S = a2𝑡22 /2. По условию задачи 2t1 = t2, отсюда следует, что 4a2 = a1. Подставляя данные в наши формулы получим, что gsinα + µgcosα = 4(gsinα - µgcosα), и теперь мы можем вывести окончательную формулу для нахождения µ, µ = 0,6tgα, tgα потому что по формуле sinα/cosα = tg α. Ответ: µ = 0,6tgα. Задача № 5. Дано: m 1 = 1 кг., m 2 = 2 кг., h 0 = 0,2 м . Найти: h. Решение: В первую очередь сразу же заметим, что эти две вертикаль ные цилиндры соединены внизу трубкой, а отсюда следует, что два цилиндра представляют сообщающиеся сосуды. Если мы увеличим массу 1-го поршня до массы 2-го поршня, то равновесие наступит лишь в том случае, если 1 поршень Опустится на самое дно своего цилиндра, и в этом случае весь газ перейдет во 2 цилиндр. Так как по условию задачи Температура газа постоянна, то и объем тоже постоянный. Из выше перечисленного следует, что S1h0 + S2h0 =S2h, где S1 – площадь поперечного сечения 1-го поршня, S2 – площадь поперечного сечения 2 –го поршня, h – высота 2 – го поршня. Теперь постараемся вывести h, В самом начале давление, оказываемы поршнями были Равными: m1g/S1 = m2g/S2, отсюда следует, что S1/S2 = m1/m2. И вот теперь выведем окончательную формулу для расчета h, h = h0(m1/m2 + 1)= 0,2(1/2 + 1) = 0,3 метра. Ответ: h = 0,3 метра. Задача № 3. Дано: М – масса планеты; R – радиус станции; mст = 10m, Решение: Так как метеорит после столкновения застревает в станции, то их уже общая скорость будет равна V2. А скорость R/2 – расстояние до планеты. Найти: U – скорость метеорита Перед столкновением. Станции до столкновения равен V1, Скорость станции V1 можно вычислить по известной нам формуле для нахожден. Первой космической скорости: V1 =√𝐺𝑀/𝑅 По закону сохранения импульса: m 1V1 + m2V2 = m1U1 + m2U2, где U1 и U2 – скорости после соударения. Из этого закона следует, что mU + 10mV1 = 11mV2, где m – масса мете – орита. Теперь необходимо спроектировать этот Закон на Оси Y и X: 10mV1 = 11mV2x; mU = 11mV2y. Так как после столкновения станция Переходит на новую орбиту, а ее энергия Остается постоянной, то -G11mM/R + 11m(𝑉 2 2𝑥 + 𝑉 2 2𝑦)/2 = -G11mM/R/2 + 11m𝑉 2 𝑜, где V0 – скорость станции в наибольшей Приближенности к Земле. По второму Закону Кеплера V0 и V2 связаны: V0R/2 = V2xR , U =√ Ответ: U = √ Задача № 4. Дано: V – объем стального Шарика. дельта V - ? 58𝐺𝑀 𝑅 58𝐺𝑀 𝑅 Решение: По условию часть шарика погружена в ртуть, То тогда приму, что та часть шарика, которая погру – жена в ртуть, то есть объем равен V1, а V2 – это объем когда вода полностью закроет шарик. pсV = ppV1, где p – плотности стали и ртути. Выталкивающая сила на шарик, со стороны воды будет равна pв(V – V2). А со стороны ртути уже примет иной вид: pртV1g. Отсюда следует, что pстV = pртV2 + pв(V – V2). Я считаю, что объем погруженной в ртуть части Данного шарика уменьшится, потому что Pрт>pст, то V1>V2. Ответ: Уменьшится. Задача № 10. Дано: Рисунок., R – сопротивление, U – напряжение. Решение: R1 = R/2 + R/2/R + R/2 = 5/6 R, Теперь уже по Закону Ома найдем общую силу тока В цепи. I = U/(5/6)/R = 6U/5R U2 - ? Задача № 6. Дано: t 1 улица = -20, t 1 комната= +20, t 2 улица = -40, t 2 комната = +10 Решение: Q = cm(t2 –t1), следуя этой формуле запишем следую щее: с(t – t1комн) – эта теплота ко-ая батарея передает в комнате. t – t1комн – теплота уходящая на улицу. с(t – t1комн) = с1(t – t1улицы). И так же во втором случае: с(t – t2комн) = с1(t – t2улицы) , Поделим первое уравнение на второе: с(t – t1комн)/ с(t – t2комн) = с1(t – t1улицы)/ с1(t – t2ул) теперь выразим t: t = (t2к *t1у – t1к*t2у)/(t2к + t1у – t2у – t1к) подставив численные значения, получим: t = ( 10 *(-20) – 20*(-40))/(10 – 20 + 40 -20) = + 85 гр. Ответ: 85 градусов по Цельсию. t батареи - ? Задача № 9. Решение: 1\Rобщ = 1\R1 + 1\R2…. Для параллельного соединения Я считаю, что сначала нужно рассмотреть резисторы которые лежат как бы параллельно друг другу. И потом по формуле для последовательного и параллельного соединения найдем сопротивления между точками А и B как показано на рисунке.



