Методические указания по выполнению Контрольной работы по дисциплине «Прикладная механика»

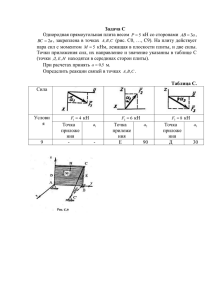
Ставропольский Государственный Медицинский
Университет
Методические указания по выполнению
Контрольной работы по дисциплине
«Прикладная механика»
Ставрополь
СОДЕРЖАНИЕ
1 ФОРМУЛИРОВКА ЗАДАНИЯ И ЕГО ОБЪЕМ……………….….….3
2 ОБЩИЕ ТРЕБОВАНИЯ К НАПИСАНИЮ КОНТРОЛЬНОЙ
РАБОТЫ………………………………………………….…………………..….…..3
3
РЕКОМЕНДАЦИИ
ПО
ОРГАНИЗАЦИИ
ВЫПОЛНЕНИЯ
КОНТРОЛЬНОЙ РАБОТЫ….………………………………………………..…...3
..
4 ПОРЯДОК ЗАЩИТЫ И ОТВЕТСТВЕННОСТЬ СТУДЕНТА
ЗА ВЫПОЛНЕНИЕ КОНТРОЛЬНОЙ РАБОТЫ………………………………....45
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ……….…………………46
2
1 ФОРМУЛИРОВКА ЗАДАНИЯ И ЕГО ОБЪЕМ
КОНТРОЛЬНОЙ работа выполняется с целью освоения статических
расчетов
и состоит из 3-х заданий по вариантам, выполнение которых
предусматривает:
- определение реакций опор твердого тела;
- определение реакция опор и сил в стержнях плоской фермы;
- определение реакций опор составной конструкции (система из двух тел).
2 ОБЩИЕ ТРЕБОВАНИЯ К НАПИСАНИЮ
КОНТРОЛЬНОЙ РАБОТЫ
Работа выполняется на листах белой бумаги формата А4 (210×297 мм)
рукописно или на компьютере в текстовом редакторе Word. И в том и в другом
случае текст выполняется с полями: верхним и нижним– 20 мм; левым – 30 мм;
правым – 15 мм.
При компьютерном наборе используется шрифт Times New Roman размером
14 пунктов с красной строкой 1,25 см. Ориентация книжная, межстрочный интервал
полуторный, выравнивание по ширине, страницы нумеруются внизу справа.
Рекомендуется снять запрет висячих строк и установить переносы в словах,
а формулы набирать в редакторе формул.
Рисунки выполняются вручную карандашом или в графическом редакторе
(AutoCAD, Kompas, Tefleks и др.). Допускается использовать компьютерный набор
текста и выполнение расчетных схем карандашом.
Курсовая работа должна иметь:
- титульный лист;
- задание на курсовую работу, выданное преподавателем;
- расчеты и расчетные схемы согласно заданию (см. примеры выполнения в
разделе 3);
- список использованной литературы, оформленный в соответствие с
требованиями ГОСТ 7.1-2003.
3 РЕКОМЕНДАЦИИ ПО ОРГАНИЗАЦИИ ВЫПОЛНЕНИЯ
КОНТРОЛЬНОЙ РАБОТЫ
Выполнение каждого задания осуществляется согласно приведенным в
соответствующих вариантах схемам и другим данным.
Задание 1. Определение реакций опор твердого тела.
Даны три схемы закрепления бруса (см. варианты). Задаваемая нагрузка и
размеры (в м) во всех случаях одинаковы.
Определить реакции опор для той схемы закрепления, при которой
исследуемая величина имеет наименьшее числовое значение.
3
Вариант 1
Р = 10 кН;
М = 6 кН·м;
q = 2 кН/м;
исследуемая реакция – YА
Вариант 2
Р = 20 кН;
М = 5 кН·м;
q = 4 кН/м;
исследуемая реакция – МА
Вариант 3
Р = 15 кН;
М = 6 кН·м;
q = 1 кН/м;
исследуемая реакция – YB
Вариант 4
4
Р = 5 кН;
М = 2 кН·м;
q = 1 кН/м;
исследуемая реакция – YВ
Вариант 5
Р = 10 кН;
М = 4 кН·м;
исследуемая реакция – ХВ
Вариант 6
Р = 6 кН;
М = 2 кН·м;
q = 1 кН/м;
исследуемая реакция – МА
Вариант 7
5
Р = 2 кН;
М = 4 кН·м;
q = 2 кН/м;
исследуемая реакция – ХА
Вариант 8
Р = 20 кН;
М = 10 кН·м;
q = 4 кН/м;
исследуемая реакция – RВ
Вариант 9
Р = 10 кН;
М = 6 кН·м;
исследуемая реакция – YА
6
Вариант 10
Р = 2 кН;
М = 4 кН·м;
q = 2 кН/м;
исследуемая реакция – ХА
Вариант 11
Р = 4 кН;
М = 10 кН·м;
q = 1 кН/м;
исследуемая реакция – RВ
Вариант 12
Р = 10 кН;
М = 5 кН·м;
q = 2 кН/м;
исследуемая реакция – YА
Вариант 13
Р = 20 кН;
М = 12 кН·м;
q = 2 кН/м;
исследуемая реакция – YА
7
Вариант 14
Р = 15 кН;
М = 4 кН·м;
q = 3 кН/м;
исследуемая реакция – YА
Вариант 15
Р = 10 кН;
М = 5 кН·м;
q = 2 кН/м;
исследуемая реакция – ХА
Вариант 16
Р = 12 кН;
М = 6 кН·м;
q = 2 кН/м;
исследуемая реакция – МА
Вариант 17
8
Р = 20 кН;
М = 4 кН·м;
q = 3 кН/м;
исследуемая реакция – YА
Вариант 18
Р = 14 кН;
М = 4 кН·м;
q = 2 кН/м;
исследуемая реакция – ХА
Вариант 19
Р = 16 кН;
М = 6 кН·м;
q = 1 кН/м;
исследуемая реакция – RB
Вариант 20
9
Р = 10 кН;
q = 4 кН/м;
исследуемая реакция – YА
Вариант 21
Р = 20 кН;
М = 10 кН·м;
q = 2 кН/м;
исследуемая реакция – МА
Вариант 22
Р = 6 кН;
М = 6 кН·м;
q = 1 кН/м;
исследуемая реакция – YА
Вариант 23
Р = 10 кН;
М = 4 кН·м;
q = 2 кН/м;
исследуемая реакция – МА
Вариант 24
10
Р = 4 кН;
М = 3 кН·м;
q = 1 кН/м;
исследуемая реакция – YА
Вариант 25
Р = 10 кН;
М = 10 кН·м;
q = 2 кН/м;
исследуемая реакция – ХА
Вариант 26
11
Р = 20 кН;
М = 5 кН·м;
q = 2 кН/м;
исследуемая реакция – МА
Вариант 27
Р = 10 кН;
М = 6 кН·м;
q = 1 кН/м;
исследуемая реакция – ХА
Вариант 28
Р = 20 кН;
М = 10 кН·м;
q = 2 кН/м;
исследуемая реакция – YА
Вариант 29
12
Р = 25 кН;
q = 1 кН/м;
исследуемая реакция – МА
Вариант 30
Р = 20 кН;
М = 10 кН·м;
q = 2 кН/м;
исследуемая реакция – RВ
Пример выполнения задания 1
Необходимо определить реакции опор для того способа закрепления бруса,
при котором момент МА в жесткой заделке имеет наименьшее по модулю значение,
если Р = 5 кН; М = 8 кН·м; q = 1,2 кН/м.
13
Рассмотрим
уравновешенную
систему сил. Мысленно отбросим связи, а
их действие на брус заменим реакциями.
Равномерно
распределенную
нагрузку заменим равнодействующей,
приложенной в центре отрезка, на
котором она действует
Q  q  2  1,2  2  2,4 м .
Рассмотрим схему закрепления «а». Для
определения МА составим уравнение
равновесия в виде «сумма моментов всех
сил относительно точки А равна нулю».
Это позволит устранить две неизвестные
реакции в этой точке и решать уравнение
с одним неизвестным моментом МА.
 mA ( F )  0 .
Отсюда
МА =
5
МА – Р·sin 45о·2 +М – Q·5 = 0.
2
 2  8  2 ,4  5  11,07 кН  м .
2
Рассмотрим схему закрепления
«б». Для определения МА составим
уравнение равновесия в виде «сумма
моментов всех сил относительно точки
С равна нулю». Точку С находим на
пересечении линий действия реакций
YA и ХВ, что позволит устранить эти реакции и решать уравнение равновесия с
одним неизвестным моментом МА.
14
 mС ( F )  0 .
Тогда
МА =
МА + М – Q ·5 = 0.
 8  2,4  5  4 кН  м .
Рассмотрим схему закрепления «в». Для определения МА составим
уравнение равновесия в виде «сумма
моментов всех сил относительно точки
В равна нулю». Это позволит устранить
две неизвестные реакции в точке В и
решать уравнение с одним не
известным моментом МА.
 mВ ( F )  0 .
Отсюда
МА =
2
 2 2 ) +М + Q·1 = 0.
2
МА + Р·(2
 5  3 2  8  2 ,4  1  31,61 кН  м .
Таким образом, наименьшее значение исследуемая реакция
имеет при схеме закрепления «б», а остальные реакции опор найдем, составив ещё
два уравнения равновесия:
 Fix  0
P·cos45o +XB = 0
 Fiy  0
YB – P·sin45o – Q = 0
2
 3,54 кН .
2
2
YB = 5 
 2,4  5,94 кН .
2
XB =  5 
Задание 2. Определение реакции опор и сил в стержнях плоской
фермы.
Определить реакции опор фермы от заданной нагрузки (см. варианты), а
также силы во всех её стержнях методом вырезания узлов.
Дополнительно определить силы в трех указанных в задании стержнях
методом Риттера.
15
Вариант 1
Р1 = 4 кН;
Р2 = 9 кН;
Р3 = 2 кН;
а = 2 м;
α = 30о;
номера стержней: 3, 8, 9
Вариант 2
Р1 = 10 кН;
Р2 = 3 кН;
Р3 = 4 кН;
а = 2,5 м;
α = 60о;
номера стержней: 2, 5, 7
Вариант 3
Р1 = 2 кН;
Р2 = 12 кН;
Р3 = 6 кН;
а = 3 м;
α = 60о;
номера стержней: 4, 5, 10
16
Вариант 4
Р1 = 10 кН;
Р2 = 10 кН;
Р3 = 5 кН;
а = 4 м;
α = 60о;
номера стержней: 5, 6, 11
Вариант 5
Р1 = 2 кН;
Р2 = 4 кН;
Р3 = 2 кН;
h = 2 м;
α = 60о;
номера стержней: 4, 5, 10
Вариант 6
Р1 = 3 кН;
Р2 = 7 кН;
Р3 = 5 кН;
а = 4 м;
h = 3 м;
номера стержней: 4, 5, 10
17
Вариант 7
Р1 = 4 кН;
Р2 = 6 кН;
Р3 = 3 кН;
а = 4 м;
α = 60о;
номера стержней: 4, 6, 12
Вариант 8
Р1 = 5 кН;
Р2 = 7 кН;
Р3 = 7 кН;
а = 3,2 м;
α = 45о;
номера стержней: 3, 4, 5
Вариант 9
Р1 = 10 кН;
Р2 = 8 кН;
Р3 = 2 кН;
а = 5 м;
α = 60о;
номера стержней: 6,
7, 12
18
Вариант 10
Р1 = 3 кН;
Р2 = 4 кН;
Р3 = 5 кН;
а = 4,4 м;
h = 3,3 м;
номера стержней: 3, 5; 7
Вариант 11
Р1 = 2 кН;
Р2 = 6 кН;
Р3 = 8 кН;
а = 2,5 м;
h = 3 м;
номера стержней: 2,
7; 8
Вариант 12
Р1 = 5 кН;
Р2 = 7 кН;
Р3 = 2 кН;
а = 4 м;
α = 60о;
номера стержней: 4, 5; 10
19
Вариант 13
Р1 = 4 кН;
Р2 = 6 кН;
Р3 = 2 кН;
а = 4,8 м;
h = 3,6 м;
номера стержней: 4,
5; 10
Вариант 14
Р1 = 3 кН;
Р2 = 5 кН;
Р3 = 5 кН;
а = 3 м;
α = 60о;
номера стержней: 5, 6;
8
Вариант 15
Р1 = 2 кН;
Р2 = 2 кН;
Р3 = 10 кН;
а = 4 м;
h = 6 м;
номера стержней: 2, 6; 9
20
Вариант 16
Р1 = 5 кН;
Р2 = 6 кН;
Р3 = 2 кН;
а = 5 м;
α = 60о;
номера стержней: 3, 5;
6
Вариант 17
Р1 = 4 кН;
Р2 = 4 кН;
Р3 = 10 кН;
а = 4 м;
h = 6 м;
номера стержней: 4, 7;
8
Вариант 18
Р1 = 5 кН;
Р2 = 2 кН;
Р3 = 8 кН;
h = 5 м;
α = 60о;
номера стержней: 1; 4; 8
21
Вариант 19
Р1 = 8 кН;
Р2 = 4 кН;
Р3 = 10 кН;
а = 5 м;
h = 10 м;
α = 60 о;
номера стержней: 4; 5; 7
Вариант 20
Р1 = 2 кН;
Р2 = 3 кН;
Р3 = 5 кН;
а = 4 м;
h = 6 м;
номера стержней: 5; 6; 8
Вариант 21
Р1 = 3 кН;
Р2 = 2 кН;
Р3 = 7 кН;
а = 6 м;
α = 45 о;
номера стержней: 5;
8; 9
22
Вариант 22
Р1 = 4 кН;
Р2 = 2 кН;
Р3 = 9 кН;
а = 4 м;
α = 45 о;
номера стержней: 2; 6;
8
Вариант 23
Р1 = 5 кН;
Р2 = 8 кН;
Р3 = 8 кН;
а = 4 м;
h = 9 м;
α = 30 о;
номера стержней: 4;
7; 9
Вариант 24
Р1 = 6 кН;
Р2 = 10 кН;
Р3 = 2 кН;
а = 3,6 м;
α = 45 о;
номера стержней: 4; 5;
10
23
Вариант 25
Р1 = 7 кН;
Р2 = 10 кН;
Р3 = 5 кН;
а = 4,4 м;
h = 3,3 м;
номера стержней: 8;
10; 11
Вариант 26
Р1 = 8 кН;
Р2 = 12 кН;
Р3 = 2 кН;
а = 4 м;
α = 30 о;
номера
стержней: 4; 5;
9
Вариант 27
Р1 = 9 кН;
Р2 = 4 кН;
Р3 = 4 кН;
а = 4 м;
h = 3 м;
номера
стержней: 5; 9;
11
24
Вариант 28
Р1 = 10 кН;
Р2 = 5 кН;
Р3 = 3 кН;
а = 5 м;
α = 30 о;
номера
стержней: 3; 5;
6
Вариант 29
Р1 = 12 кН;
Р2 = 8 кН;
Р3 = 2 кН;
а = 6 м;
α = 45 о;
номера
стержней: 5;
6; 11
Вариант 30
Р1 = 5 кН;
Р2 = 10 кН;
Р3 = 4 кН;
а = 4 м;
h = 2 м;
номера
стержней: 6;
7; 12
25
Пример выполнения задания 2
Дано: схема плоской фермы, Р1 = 2 кН; Р2 = 4 кН; Р3 = 6 кН; а = 4 м; h = 3
м.
Покажем внешние силы, приложенные к ферме. Отбросим опоры и заменим
их действие на ферму силами реакций. Обозначим буквами все узлы.
Так как линия действия реакции опоры А неизвестна, определим её
составляющие по двум координатным осям. Реакцию опоры в точке В направим
вертикально вверх.
Составим уравнения равновесия фермы в целом. Поскольку в точке А две, а
в точке В одна неизвестная реакция, составим уравнение равновесия в виде «сумма
моментов всех сил относительно точки А равна нулю». Это позволит решить
уравнение относительно одной неизвестной величины RB.
 mА ( F )  0
Отсюда
RB ∙a =0
233  423
RB  
 10,5 кН .
4
Р1∙3h +Р2·2h +
Составив два других уравнения равновесия, определим остальные реакции
опор.
 Fiõ  0 Õ A  P1  Ð2  0 .
26
Õ A  P1  Ð2  2  4  6
 Fiy  0 YA  RB  P3  0 .
Отсюда
Отсюда
кН.
YA   RB  P3  10 ,5  6  16,5
кН.
Полная реакция опоры А будет равна
R A  X A2  YA2  6 2  16 ,5 2
= 17,56 кН.
Стержни, сходящиеся в узле фермы, являются для узлового соединения
связями. Отбросим связи и заменим их действие на узлы реакциями.
Направления всех реакций условно
примем внутрь стержней, предполагая, что
стержни растянуты. Если в результате
решения реакция получится отрицательной,
стержень сжат.
Предварительно определим:
sin  
h
a2  h2

3
4 2  32

3
5

4
5
;
cos  
a
a 2  h2

4
4 2  32
.
Рассмотрим условия равновесия каждого отдельного узла, мысленно
вырезая его из фермы, в чем и заключается сущность способа вырезания узлов.
Для каждого узла будем составлять по два уравнения равновесия
следующего вида:
 Fix  0 ,  Fiy  0 .
Причем первым составляется то
уравнение, в котором только одна неизвестная величина.
Начнем с узла Н, в котором две неизвестные реакции, что соответствует
количеству уравнений равновесия.
 Fix  0
– S1H cosα – P1 = 0
25
 2 ,5 кН (стержень сжат)
4
 Fiy  0 – S1H sinα – S2H = 0
S1 H  
27
2 ,5  3
 1,5 êÍ
5
S2 H 
(стержень растянут)
Поскольку S1Е = S1H, перейдем к рассмотрению узла Е, в котором теперь
осталось только две неизвестные величины: S3E и S4E.
Для этого узла уравнения равновесия будут иметь следующий вид.
 Fix  0
S1Е cosα + S3Е = 0
2 ,5  4
 2 кН (стержень растянут)
5
 Fiy  0 – Р3 – S4Е + S1Е sinα = 0
S3 Е 
3
S4 Е  2 ,5   6  7 ,5 кН
5
(стержень сжат).
Поскольку S3Е = S3F и S2Н = S2F, перейдем к рассмотрению узла F, в котором
теперь осталось только две неизвестные величины: S5F и S6F.
S5 F
 Fix  0 S3F – S3Е cosα – Р2 = 0
( 2  4 ) 5

 7 ,5 êÍ (стержень сжат)
4
 Fiy  0 – S2F – S6F – S5F sinα = 0
S6 F  1,5  7 ,5 
Для узла С.
3
 12 êÍ
5
 Fix  0
S7C – S5C cosα = 0
S7 Ñ  7 ,5
4
 6 êÍ
5
 Fiy  0
 Fix  0
(стержень сжат)
S4C – S8C + S5C sinα = 0
S8Ñ  7 ,5  7 ,5 
Для узла D.
(стержень сжат).
3
 12 êÍ
5
(стержень сжат).
S7D – S9D cosα = 0
28
S 9 D  6
 Fiy  0
5
 7 ,5 êÍ
4
(стержень сжат)
S6D – S10D – S9D sinα = 0
S10 D  6  7 ,5 
Для узла А.
 Fix  0
3
 10,5 êÍ
5
(стержень растянут).
ХА + S11А + S9А cosα = 0
4
S11 À  6  7 ,5  0 êÍ
5
Узел В рассматривать не нужно
полученные результаты в таблицу.
Номер
1
2
3
4
стержня
Знак силы
+
+
Сила, кН
2,5 1,5
2
7,5
(стержень не нагружен).
– все силы в стержнях определены. Сведем
5
6
7
8
9
10
11
7,5
12,0
6,0
12,0
7,5
+
10,5
0
Способом сечений (Риттера) определим силы в стержнях 4, 5 и 8. Сначала
мысленно разрежем ферму сечением, проходящим через стержни 4, 5 и 8. Составим
уравнения равновесия для этой части фермы.
На
этой
схеме
3
неизвестные силы, причем линии
действия двух из них сходятся в
точке F.
Составим
уравнение
равновесия вида
 mF ( F )  0
S 4  a  P3  a  P1  h  0
Отсюда
Другое
S4 
 P3  a  P1  h  6  4  2  3

 7 ,5 кН.
a
4
уравнение
равновесия
 Fix  0
или
29
 P1  S 5 cos   P2  0
 P1  P2 ( 2  4 ) 5
S5 

 7 ,5
cos 
4
позволит
определить
кН.
Для
определения
силы в стержне 8 мысленно
разрежем ферму сечением,
проходящим через стержни 8,
9 и 10. Поскольку линии
действия сил в стержнях 9 и
10 сходятся в точке D,
составим уравнение равновесия вида
 mF ( F )  0  S 8  a  YA  a  X A  h  0
 YA  a  X A  h  16 ,5  4  6  3
Тогда S 8 

 12
a
4
кН.
Полученные результаты соответствуют данным, полученным способом
вырезания узлов.
Задание 3. Определение реакция опор составной конструкции
Конструкция состоит из двух частей. Установить, при каком способе
соединения (с помощью шарнира или с помощью скользящей заделки) частей
конструкции модуль реакции, указанный в задании (см. варианты), имеет
наименьшее значение.
Для этого способа соединения определить реакции всех опор, а также
соединения в точке С.
30
Вариант 1
Р1 = 5 кН;
М = 24 кН·м;
q = 0,8 кН/м;
исследуемая реакция –
ХА
Вариант 2
Р1 = 6 кН;
Р2 = 10 кН;
М = 22 кН·м;
q = 1 кН/м;
исследуемая
реакция – RА
Вариант 3
Р1 = 7 кН;
Р2 = 9 кН;
М = 20 кН·м;
q = 1.2 кН/м;
исследуемая реакция –
RВ
31
Вариант 4
Р1 = 8 кН;
М = 18 кН·м;
q = 1,4 кН/м;
исследуемая реакция
– МА
Вариант 5
Р1 = 9 кН;
М = 16 кН·м;
q = 1,6 кН/м;
исследуемая
реакция – RА
Вариант 6
Р1 = 10 кН;
Р2 = 8 кН;
М = 25 кН·м;
q = 1,8 кН/м;
исследуемая реакция –
МА
32
Вариант 7
Р1 = 11 кН;
Р2 = 7 кН;
М = 20 кН·м;
q = 2 кН/м;
исследуемая реакция –
RВ
Вариант 8
Р1 = 12 кН;
Р2 = 6 кН;
М = 15 кН·м;
q = 2,2 кН/м;
исследуемая
реакция – МА
Вариант 9
Р1 = 13 кН;
М = 10 кН·м;
q = 2,4 кН/м;
исследуемая реакция –
ХА
33
Вариант 10
Р1 = 14 кН;
М = 12 кН·м;
q = 2,6 кН/м;
исследуемая реакция –
RА
Вариант 11
Р1 = 15 кН;
Р2 = 5 кН;
М = 14 кН·м;
q = 2,8 кН/м;
исследуемая реакция –
RD
Вариант 12
Р1 = 12 кН;
Р2 = 4 кН;
М = 16 кН·м;
q = 3 кН/м;
исследуемая реакция
– RВ
34
Вариант 13
Р1 = 9 кН;
Р2 = 6 кН;
М = 18 кН·м;
q = 3,2 кН/м;
исследуемая реакция
– RА
Вариант 14
Р1 = 6 кН;
М = 20 кН·м;
q = 3,4 кН/м;
исследуемая реакция –
МА
Вариант 15
Р1 = 5 кН;
Р2 = 8 кН;
М = 22 кН·м;
q = 3,6 кН/м;
исследуемая реакция
– МВ
35
Вариант 16
Р1 = 7 кН;
Р2 = 10 кН;
М = 14 кН·м;
q = 3,8 кН/м;
исследуемая реакция
– RВ
Вариант 17
Р1 = 9 кН;
Р2 = 12 кН;
М = 26 кН·м;
q = 4 кН/м;
исследуемая реакция –
RА
Вариант 18
Р1 = 11 кН;
Р2 = 10 кН;
М = 18 кН·м;
q = 3,5 кН/м;
исследуемая
реакция – МВ
36
Вариант 19
Р1 = 13 кН;
Р2 = 9 кН;
М = 30 кН·м;
q = 3 кН/м;
исследуемая реакция –
МВ
Вариант 20
Р1 = 15 кН;
Р2 = 8 кН;
М = 25 кН·м;
q = 2,5 кН/м;
исследуемая реакция
– RВ
Вариант 21
Р1 = 10 кН;
Р2 = 7 кН;
М = 20 кН·м;
q = 2 кН/м;
исследуемая реакция –
RA
Вариант 22
37
Р1 = 5 кН;
Р2 = 6 кН;
М = 15 кН·м;
q = 1,5 кН/м;
исследуемая реакция –
RA
Вариант 23
Р1 = 8 кН;
Р2 = 5 кН;
М = 10 кН·м;
q = 1,4 кН/м;
исследуемая реакция –
RA
Вариант 24
Р1 = 11 кН;
Р2 = 4 кН;
М = 5 кН·м;
q = 1,3 кН/м;
исследуемая
реакция – МA
Вариант 25
38
Р1 = 14 кН;
Р2 = 6 кН;
М = 7 кН·м;
q = 1,2 кН/м;
исследуемая
реакция – RВ
Вариант 26
Р1 = 12 кН;
Р2 = 8 кН;
М = 9 кН·м;
q = 1,1 кН/м;
исследуемая реакция –
RВ
Вариант 27
Р1 = 10 кН;
Р2 = 7 кН;
М = 11 кН·м;
q = 1 кН/м;
исследуемая реакция –
ХA
39
Вариант 28
Р1 = 8 кН;
Р2 = 9 кН;
М = 13 кН·м;
q = 1,2 кН/м;
исследуемая реакция
– RA
Вариант 29
Р1 = 6 кН;
Р2 = 10 кН;
М = 15 кН·м;
q = 1,4 кН/м;
исследуемая
реакция – МA
Вариант 30
Р1 = 10 кН;
Р2 = 12 кН;
М = 17 кН·м;
q = 1,6 кН/м;
исследуемая реакция
– МВ
40
Пример выполнения задания 3
Определить реакции опор, а также соединения С для того способа
сочленения двух тел (шарнир или скользящая заделка), при котором модуль реакции
опоры А имеет наименьшее значение.
Исходные данные:
Р1 = 5 кН;
Р2 = 7 кН;
М = 22 кН;
q = 2 кН/м;
α = 60о
Определим равнодействующую
приложим в центре участка
распределенной
Q  q4  24  8
нагрузки,
которую
кН.
Рассмотрим конструкцию при шарнирном соединении в точке С. Мысленно
отбросим связи и заменим их силами реакции. Поскольку направления реакций в
точках А и В не известны, используем их составляющие по осям координат.
Рассмотрим равновесие конструкции в целом. Неизвестными величинами в
этом случае будут четыре составляющие реакций ХА, YA, XB и YВ.
.
41
Чтобы снизить число неизвестных в уравнении равновесия, составим его в
виде суммы моментов относительно точки В.
 m ( F )  0
P1 cos 60o  3  P1 sin 60o  8  Q  1  YA  5  X A  1 
 M  P2 1,5 2  12  0
Получим уравнение X A  5YA  24 ,74 .
Далее рассмотрим систему уравновешенных сил, приложенных к той части
конструкции, которая расположена левее шарнира С.
Составим уравнение равновесия вида
 m ( F )  0 .
P1 sin 60  6  Q  2  YA  3  X A  4  0
Получим 4 X A  3Y A  41,98 .
Решая систему уравнений, получим Õ À  7 ,97
o
кН,
YÀ  3 ,36
кН.
42
Модуль реакции опоры А составит
R A  X A2  YA2  ( 7 ,97 )2  3,36 2
= 8,65 кН.
Рассмотрим равновесие левой части конструкции при скользящей заделке.
 Fix  0 …  P1 cos 60 o  Q  X A  0
X A  P1 cos 60 o  Q  5  0 ,5  8  5 ,5 кН.
А из уравнения равновесия для всей конструкции Y A  3 ,85
Тогда
кН.
Модуль реакции опоры А при скользящей заделке в точке С будет равен
R A  X A2  YA2  ( 5 ,5 )2  3,85 2
=
= 6,71 кН.
43
Таким образом, согласно заданию следует определять реакции опор и
соединения С для способа сочленения тел со скользящей заделкой.
Для определения силы реакции в скользящей заделке составим уравнение
равновесия.
o
 Fió  0 …  P1 sin 60  YA  YC  0
Отсюда
YC  P1 sin 60 o  YA  5  0 ,87  3 ,85  0 ,48
кН.
Момент в скользящей заделке и реакцию опоры В найдем, составляя
уравнения равновесия для той части конструкции, которая расположена правея
скользящей заделки.
 m ( F )  0
M C  YC  2  M  P2 1,5 2  12  0
M C  YC  2  M  P2 1,5 2  12  8 ,44
 Fiõ  0
 P2 cos   X B  0
Отсюда X B  P2 cos   7  0 ,83  5 ,82 кН.
Отсюда
кН.
44
 Fiy  0
 YC  YB  P2 sin   0
Отсюда YB  YC  P2 sin   0 ,48  7  0 ,55  4 ,36
R A  X A2  YA2  5 ,82 2  4 ,37 2
кН.
= 7,28 кН.
4 ПОРЯДОК ЗАЩИТЫ И ОТВЕТСТВЕННОСТЬ СТУДЕНТА
ЗА ВЫПОЛНЕНИЕ КОНТРОЛЬНОЙ РАБОТЫ
Защита контрольной работы осуществляется путем собеседования с
преподавателем, в ходе которого студент должен грамотно объяснить ход решения
задания и проанализировать полученные результаты. Преподаватель вправе
предложить студенту решение задачи, аналогичной любому из заданий. Работа
оценивается
«отлично»,
«хорошо»,
«удовлетворительно»
или
«не
удовлетворительно».
45
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Тарг, С.М. Краткий курс теоретической механики [Текст]: учебник. – М.:
Высшая школа, 2010. – 416 с.
2. Яблонский, А.А. Сборник заданий для курсовых работ по теоретической
механике [Текст]: учебное пособие - М.: КноРус, 2010. – 392 с.
3. Мещерский, И.В. Задачи по теоретической механике [Текст]: учебное
пособие. – СПб.: Лань, 2010. – 448 с.
4. Шведов, А.А. Теоретическая механика: статика и кинематика [Текст]:
учебная пособие. – Ставрополь: СевКавГТИ, 2008. – 80 с.
46