Теория множествx
реклама
Раздел 1. Теория множеств.
1.1. Алгебра теории множеств.
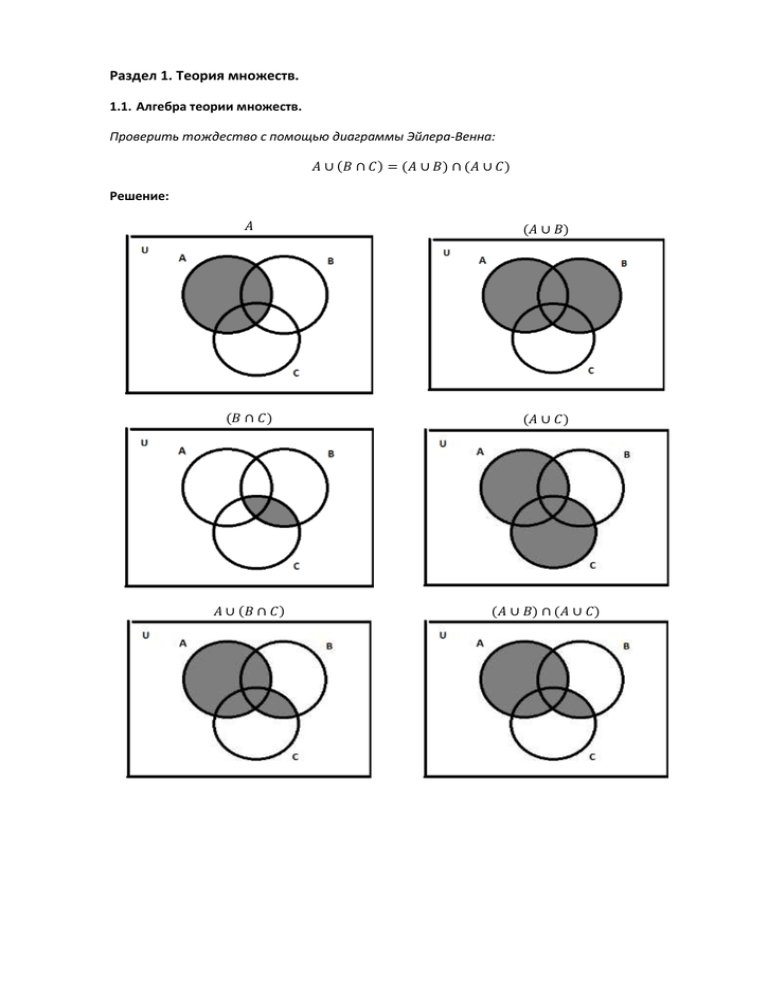
Проверить тождество с помощью диаграммы Эйлера-Венна:
𝐴 ∪ (𝐵 ∩ 𝐶) = (𝐴 ∪ 𝐵) ∩ (𝐴 ∪ 𝐶)
Решение:
𝐴
(𝐴 ∪ 𝐵)
(𝐵 ∩ 𝐶)
(𝐴 ∪ 𝐶)
𝐴 ∪ (𝐵 ∩ 𝐶)
(𝐴 ∪ 𝐵) ∩ (𝐴 ∪ 𝐶)
1.2. Алгебра нечетких множеств.
Задано универсальное множество E = {a, b, c, d, e, f, j} и три нечетких подмножества:
A = {(a|0), (b|0.3), (c|0.7),(d|1), (e|0), (f, 0.2),(j|0.9)};
B={(a|0.3),(b|1),(c|0.5),(d|0.8),(e|1), (f|0.5),(j|0.6)};
C={(a|1),(b|0.5),(c|0.5),(d|0.2), (e|0),f(0.2),(j|0.9)};
Выполнить действия:
а) (𝐴 ∩ 𝐶) ∪ 𝐵
б) 𝐴 ⊕ 𝐶
Решение:
а) (𝐀 ∩ 𝐂) ∪ 𝐁
μс (x) = 1.0 − μc (x)
𝜇(𝐴∩𝐶) (𝑥) = min(𝜇𝐴 (𝑥), 𝜇𝐶 (𝑥))
𝜇(A∩C)∪B (𝑥) = max (𝜇(𝐴∩𝐶) (𝑥), 𝜇𝐵 )
a
b
c
d
e
f
j
μс (x)
𝜇𝐴 (𝑥)
𝑥
0
0.3
0.7
1
0
0.2
0.9
0
0.5
0.5
0.8
1
0.8
0.1
𝜇(𝐴∩𝐶) (𝑥)
0
0.3
0.5
0.8
0
0.2
0.1
𝜇(A∩C)∪B (𝑥)
𝜇𝐵
0.3
1
0.5
0.8
1
0.5
0.6
0.3
1
0.5
0.8
1
0.5
0.6
(A ∩ C) ∪ B = {(𝑎|0.3), (𝑏|1), (𝑐|0.5), (𝑑|0.8), (𝑒|1), (f|0.5), (j|0.6)}
б) 𝐀 ⊕ 𝐂
A ⊕ C = (A − C) ∪ (C − A) = (A ∩ C) ∪ (C ∩ A) = (𝐴 ∪ 𝐶) ∪ (A ∩ C)
μ𝐴∪𝐶 (x) = max(μ𝐴 (x), μ𝐶 (x))
μ𝐴∪𝐶 (x) = 1.0 − μ𝐴∪𝐶 (x)
μA∩C (x) = min(μ𝐴 (x), μ𝐶 (x))
μ(𝐴∪𝐶)∪(A∩C) (x) = max(μ𝐴∪𝐶 (x), μA∩C (x))
𝑥
a
b
c
d
e
f
j
𝜇𝐴 (𝑥)
0
0.3
0.7
1
0
0.2
0.9
𝜇𝐶 (𝑥)
1
0.5
0.5
0.2
0
0.2
0.9
𝜇(𝐴∪𝐶) (𝑥)
1
0.5
0.7
1
0
0.2
0.9
𝜇A∩C (𝑥)
𝜇𝐴∪𝐶 (𝑥)
0
0.5
0.3
0
1
0.8
0.1
0
0.3
0.5
0.2
0
0.2
0.9
𝜇(𝐴∪𝐶)∪(A∩C) (𝑥)
0
0.5
0.5
0.2
1
0.8
0.9
A ⊕ C = {(𝑎|0), (𝑏|0.5), (𝑐|0.5), (𝑑|0.2), (𝑒|1), (f|0.8), (j|0.9)}
1.3. Отношения.
a) Построить матрицу и граф бинарного отношения «быть в сумме чисто мнимым
числом» на множестве A = {1+2i, -1-3i, -2+4i, 2-5i, 6}, определить тип этого отношения.
Решение:
Матрица отношения:
1+2i
-1-3i
-2+4i
2-5i
6
1+2i
0
1
0
0
0
-1-3i
1
0
0
0
0
-2+4i
0
0
0
1
0
2-5i
0
0
1
0
0
6
0
0
0
0
0
Элементы отношения:
𝑅 ⊂ 𝐴 × 𝐴 = {(1 + 2𝑖, −1 − 3𝑖), (−1 − 3𝑖, 1 + 2𝑖), (−2 + 4𝑖, 2 − 5𝑖), (2 − 5𝑖, −2 + 4𝑖)}
Граф отношения:
b) На конечном множестве с помощью перечисления задано отношение:
R={(1;1),(2;1),(1;2),(2;4),(4;2),(1;4);(4;1)}. Построить матрицу отношения. Выяснить,
обладает ли данное отношение свойствами рефлексивности, антирефлексивности,
симметричности, антисиметричности и транзитивности. Установить, является ли
данное отношение отношением порядка или эквивалентности.
Решение:
Матрица отношения:
1
2
4
1
1
1
1
2
1
0
1
4
1
1
0
1) R не является рефлексивным, поскольку (2,2) ∉ 𝑅 и (4,4) ∉ 𝑅
2) R не является антирефлексивным, поскольку (1,1) ∈ 𝑅
3) R является симметричным поскольку (1,2) ∈ 𝑅 → (2,1) ∈ 𝑅,
(2,4) ∈ 𝑅 → (4,2) ∈ 𝑅, и (1,4) ∈ 𝑅 → (4,1) ∈ 𝑅
4) R не является антисимметричным, поскольку (1,2) ∈ 𝑅 и (2,1) ∈ 𝑅, но (1,2) ≠ (2,1)
5) R – транзитивно, поскольку
для 1,2 и 4: (1,2) ∈ 𝑅, (2,4) ∈ 𝑅 и (1,4) ∈ 𝑅
для 1, 4 и 2: (1,4) ∈ 𝑅, (4,2) ∈ 𝑅 и (1,2) ∈ 𝑅
для 4, 1 и 2: (4,1) ∈ 𝑅, (1,2) ∈ 𝑅 и (4,2) ∈ 𝑅
для 4, 2 и 1: (4,2) ∈ 𝑅, (2,1) ∈ 𝑅 и (4,1) ∈ 𝑅
для 2, 4 и 1: (2,4) ∈ 𝑅, (4,1) ∈ 𝑅 и (2,1) ∈ 𝑅
для 2, 1 и 4: (2,1) ∈ 𝑅, (1,4) ∈ 𝑅 и (2,4) ∈ 𝑅
6) R не является отношение эквивалентности, т.к оно не рефлексивно.
7) R не является отношение порядка так как оно не антисимметрично.
1.4. Соответствия.
Для заданных множеств A и B установить тип соответствия <G, A, B>.
𝐴 = {𝑥: |𝑥 − 1| ≤ 1}
𝐵 = {𝑦: |𝑦| ≤ 2}
𝐺 = {(𝑥, 𝑦)|𝑥 ∈ 𝐴, 𝑦 ∈ 𝐵, 𝑦 = 2(𝑥 + 1)}
Решение:
График соотвествия:
0 ≤ 𝑥 ≤ 2, −2 ≤ 𝑦 ≤ 2
Соответствие <G, A. B>:
1)
2)
3)
4)
5)
Не полное, т.к. 𝐺 ≠ 𝐴 × 𝐵
Функциональное и инъективное, т.к. 𝑦(𝑥1 ) ≠ 𝑦(𝑥2 ) по свойству линейной функции y =2x+2
Всюдуопределенное, т.к 𝐺1 = 𝐴
Не суръективное, т.к. 𝐺2 ≠ 𝐵
Не биективное, поскольку оно не суръективно.
1.5. Декартово произведение множеств.
Описать на языке теории множеств запрос к базе данных о нахождении указанного
множества:
«Найти множество иногородних студентов института, поступивших по результатам ЕГЭ,
обучающихся на втором курсе, с указанием их фамилий и результатами ЕГЭ по каждому из
вступительных испытаний»
Решение:
Базовые множества:
1)
2)
3)
4)
5)
6)
Категории студентов: S = {местные, иногородние, иностранные}
Виды вступительных испытаний: E={ЕГЭ, тест , устно }
Курсы: K={1,2,3,4,5}
Фамилии: N={Иванов, Петров, Сидоров,….}
Оценки: 𝑀 = {𝑚 ∈ ℤ|0 ≤ 𝑚 ≤ 100}
Предметы: P={математика, физика, русский язык}
Отношения связи:
1)
2)
3)
4)
5)
«Учиться на курсе»: 𝑅1 ⊂ 𝑁 × 𝐾 = {(𝑛, 𝑘)|𝑛 ∈ 𝑁, 𝑘 ∈ 𝐾}
“Категория студента”: 𝑅2 ⊂ 𝑁 × 𝑆 = {(𝑛, 𝑠)|𝑛 ∈ 𝑁, 𝑠 ∈ 𝑆}
“Вид вступительных испытаний студента”: 𝑅3 ⊂ 𝑁 × 𝐸 = {(𝑛, 𝑒)|𝑛 ∈ 𝑁, 𝑒 ∈ 𝐸}
“Оценка за экзамен”: 𝑅4 ⊂ 𝑃 × 𝑀 = {(𝑝, 𝑚)|𝑝 ∈ 𝑃, 𝑚 ∈ 𝑀}
“Студент сдавал экзамен” 𝑅5 ⊂ 𝑁 × 𝑃 = {(𝑛, 𝑝)|𝑝 ∈ 𝑃, 𝑛 ∈ 𝑁}
Запрос:
𝑄 = {(𝑛, 𝑝, 𝑚)|∃ 𝑛 ∈ 𝑀, 𝑝 ∈ 𝑃, 𝑚 ∈ 𝑀, 𝑠 ∈ 𝑆, 𝑒 ∈ 𝐸,
𝑘 ∈ 𝐾 & 𝑛𝑅1 𝑘 & 𝑛𝑅2 𝑠 & 𝑛𝑅3 𝑒 & 𝑛𝑅5 𝑝 & 𝑝𝑅4 𝑚 & 𝑒 = ЕГЭ & 𝑠 = иногородние & 𝑘
= 1}











