Стартовая работа в 5 классе
реклама
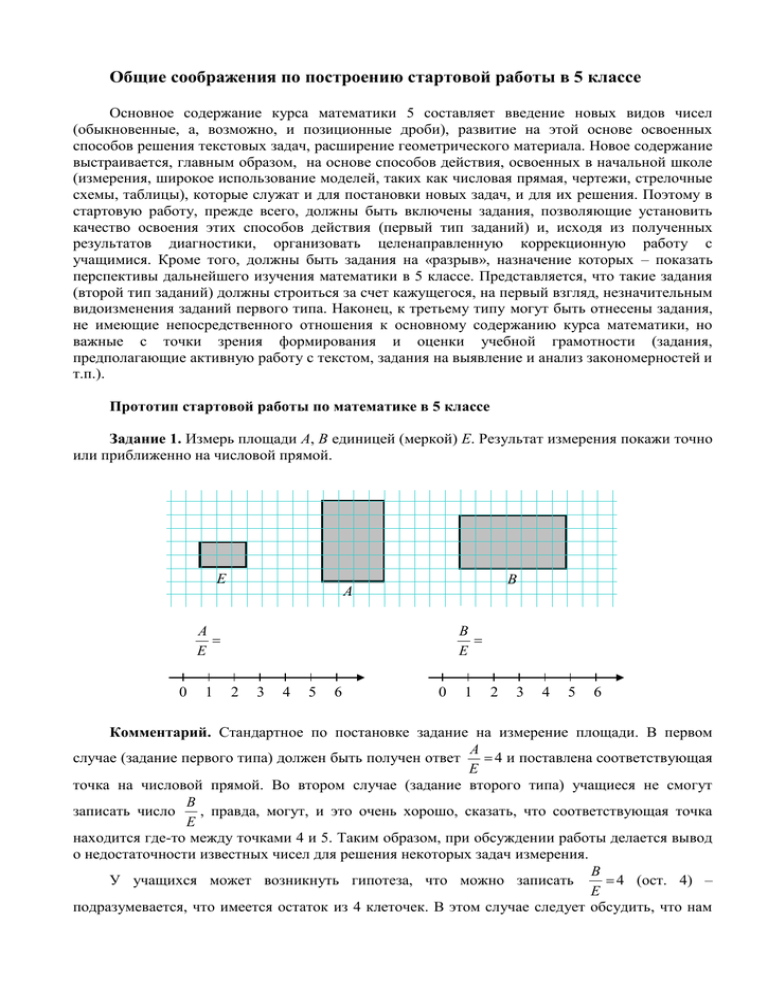
Общие соображения по построению стартовой работы в 5 классе Основное содержание курса математики 5 составляет введение новых видов чисел (обыкновенные, а, возможно, и позиционные дроби), развитие на этой основе освоенных способов решения текстовых задач, расширение геометрического материала. Новое содержание выстраивается, главным образом, на основе способов действия, освоенных в начальной школе (измерения, широкое использование моделей, таких как числовая прямая, чертежи, стрелочные схемы, таблицы), которые служат и для постановки новых задач, и для их решения. Поэтому в стартовую работу, прежде всего, должны быть включены задания, позволяющие установить качество освоения этих способов действия (первый тип заданий) и, исходя из полученных результатов диагностики, организовать целенаправленную коррекционную работу с учащимися. Кроме того, должны быть задания на «разрыв», назначение которых – показать перспективы дальнейшего изучения математики в 5 классе. Представляется, что такие задания (второй тип заданий) должны строиться за счет кажущегося, на первый взгляд, незначительным видоизменения заданий первого типа. Наконец, к третьему типу могут быть отнесены задания, не имеющие непосредственного отношения к основному содержанию курса математики, но важные с точки зрения формирования и оценки учебной грамотности (задания, предполагающие активную работу с текстом, задания на выявление и анализ закономерностей и т.п.). Прототип стартовой работы по математике в 5 классе Задание 1. Измерь площади А, В единицей (меркой) Е. Результат измерения покажи точно или приближенно на числовой прямой. Е В А А А Е 0 1 В Е 2 3 4 5 6 0 1 2 3 4 5 6 Комментарий. Стандартное по постановке задание на измерение площади. В первом А 4 и поставлена соответствующая случае (задание первого типа) должен быть получен ответ Е точка на числовой прямой. Во втором случае (задание второго типа) учащиеся не смогут В записать число , правда, могут, и это очень хорошо, сказать, что соответствующая точка Е находится где-то между точками 4 и 5. Таким образом, при обсуждении работы делается вывод о недостаточности известных чисел для решения некоторых задач измерения. В 4 (ост. 4) – У учащихся может возникнуть гипотеза, что можно записать Е подразумевается, что имеется остаток из 4 клеточек. В этом случае следует обсудить, что нам нужно узнать, сколько мерок Е помещается в В, а клеточки носят вспомогательный характер, мы могли их не рисовать вообще или взять другого размера, тогда в остатке их было бы друге количество. Задание 2. Для того чтобы узнать, делится ли одно число на другое, не всегда необходимо выполнять деление этих чисел. Например, известно, что если сумма цифр некоторого числа делится на 3, то и само число делится на 3; если же сумма цифр не делится на 3, то и само число не делится на 3. Это свойство получило название «признак делимости на 3». Существуют и другие признаки делимости. Какую цифру нужно подставить вместо звездочки, чтобы число 3124*501 делилось на 3 и было как можно больше? Комментарий. Задание третьего типа (учебная грамотность) – рассчитано на использование незнакомой информации, содержащейся в тексте. Кроме того важным моментом является необходимость удержания сразу двух условий: число должно делиться на 3 и быть наибольшим из возможных. При последующем обсуждении работы следует отметить, что в пятом классе учащиеся узнают, как доказывается этот и ряд других признаков делимости. Решение. Сумма цифр данного числа без цифры, замененной звездочкой, равна 16. Чтобы сумма делилась на 3, нужно добавить либо цифру 2 (16 + 2 = 18), либо 5 (16 + 5 = 21), либо 8 (16 + 8 = 24). Наибольшая из этих цифр 8, ее и нужно подставить вместо звездочки. Задание 3. Из квадратов, кругов и треугольников составляют ряд по определенному правилу. На рисунке показано начало этого ряда. Нарисуй 3 фигуры этого ряда, начиная с 50-й. Комментарий. Задание третьего типа (установление и анализ закономерностей). Второй уровень по Нежнову. Решение. Анализ приведенного фрагмента показывает, что повторяющаяся часть последовательности (период) состоит из 6 фигур. Ближайшее к 50 меньшее число, делящееся на 6, это 48. С 49 фигуры начнется очередное повторение: 49-я фигура – квадрат, 50-я – круг, 51-я – круг, 52-я – треугольник. 3 фигуры, начиная с 50-й: Задание 4. Найди неизвестные числа а и b по схеме. Если какое-то из чисел найти не удается, попробуй объяснить, почему. 30 a 6 b 8 Комментарий. Задание на работу со стрелочной схемой – одной из основных моделей, которые использовались при введении умножения и деления и будут использованы в 5 классе при введении обыкновенных дробей. Нахождение a (задание первого типа) осуществляется выделением соответствующей (верхней) треугольной схемы, из которой а = 30 : 6 = 5. Для нахождения b(задание второго типа) теперь есть все необходимые данные, но непонятно, что представляет собой результат деления 5 на 8. Это еще одно подтверждение необходимости введения «новых» чисел. От детей вполне достаточно объяснений типа «я не умею делить 5 : 8», «5 на 8 не делится» и т.п. Задание 5. Петя и Сережа измеряли площадь и периметр квадрата со стороной 3м. У Пети получилось, что площадь квадрата равна 9 м2, а периметр равен 12 м, из чего он сделал вывод, что периметр этого квадрата больше его площади. Сережа возразил Пете: «Я перевел метры в дециметры. Длина стороны квадрата равна 30 дм. Его площадь равна 900 дм2, а периметр 120 дм. Значит, площадь больше периметра». А как считаешь ты? Изложи свою точку зрения так, чтобы убедить и Петю, и Сережу в своей правоте. Комментарий. По форме – попытка вытащить коммуникацию через задание, выполняемое индивидуально. По содержанию – нужно объяснить, что персонажи сравнивают разнородные величины (площадь с периметром), а это некорректно. Задание 6. Говорят, что точка В лежит на линии между точками А и С, если двигаясь по этой линии из А в С (или из С в А) мы обязательно пройдем через точку В. Эта ситуация показана на рисунке 1. А В С Рис.1 Проведи через точки М, К, Р, показанные на рисунке 2, линию так, чтобы точка Р лежала на ней между точками М и К. М К Р Рис. 2 Комментарий. Задание построено на геометрическом материале и рассчитано на действие в соответствии с заданным определением, вопреки «житейскому» стереотипу, базирующемуся на наглядности (третий тип). По Нежнову – 2 уровень. Решение. Например, так: А В С Как вариант: Провести через 3 заданные точки линию так, чтобы каждая точка лежала на ней между двумя другими. (По Нежнову – 3 уровень). Задание 7. Решите на выбор одну из задач. Объясните свой выбор. 1) 100 учебников математики для пятого класса стóят 4600 руб. Сколько нужно потратить на покупку учебников математики для 5 "Ы" класса, если в нём 23 ученика? 2) В киоске было 100 книг общей стоимостью 4600 руб. Для библиотеки купили 23 книги. Сколько потратили на покупку? Комментарий. Задание содержит две внешне очень похожие задачи. Выбор первой из них и отказ от решения второй говорит о том, что учащийся по тексту задачи умеет отличать равномерный процесс от процесса, для которого нет достаточных оснований, чтобы считать его равномерным. Еще лучше, если учащийся явным образом аргументирует свой выбор. (Из условия первой задачи понятно, что речь идет об учебниках, имеющих одинаковую цену; во второй задаче такое условие не оговорено, что делает ее решение невозможным. Выбор только второй или обеих задач показывает, что понятие равномерного процесса учащимся не освоено. Второе умение, проверяемое данным заданием, – собственно умение определять характеристики равномерного процесса (умение решать задачу), а также проводить необходимые вычисления. При этом учащийся на свое усмотрение может пользоваться любым из имеющихся в его распоряжении средств: таблицей, составлением пропорции и т.п. Ответ: 1058 руб. Задание 8. Определи, является ли процесс, описываемый таблицей, равномерным: 1) 2) 3) X X X Y Y Y 15 12 16 8 9 6 5 4 20 10 12 8 Комментарий. В первом и втором случаях (задание первого типа) учащиеся в состоянии определить, что процессы равномерные (в сл.1 – сравнивая отношения 15 : 5 и 12 : 4, в сл. 2 – 16 : 8 и 20 : 10). В сл. 3, который может быть отнесен ко второму типу (разрыв), ни тот, ни другой способ не срабатывает (хотя возможно решение с помощью «дополнительного» события, например, Y = 3, X = 2 или Y = 36, X = 24. Но этот способ довольно экзотичный и вряд ли будет использован). При обсуждении работы отмечается, что новые числа, которые будут изучаться в 5 классе, позволят и в этом случае действовать точно так же, как в первых двух. Задание 9. Длина прямоугольника 12 см, а его ширина на 4 см меньше. Какова длина стороны квадрата, имеющего периметр, равный периметру прямоугольника? 1) Постройте схему и чертеж к задаче. 2) Начертите этот квадрат. Комментарий. Задание проверяет: а) владение элементарными геометрическими представлениями; б) умение пользоваться основными средствами моделирования – схемой и чертежом. Схема и чертеж могут выглядеть, например, так: 12 2 на 4 12 4 2 ? 4 ? Должен быть построен квадрат со стороной 10 см.





