www.internet-olimpiada.ru Интернет-портал
реклама

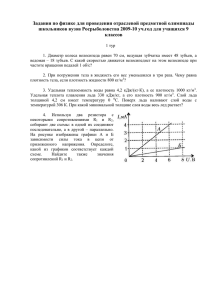
Интернет-портал www.internet-olimpiada.ru Всероссийская интернет-олимпиада e-mail: olimpiada@internet-olimpiada.ru ОТВЕТЫ К ЗАДАНИЯМ Всероссийской интернет-олимпиады по физике для 9-х классов. Примечание. Выражение «ответ дайте с точностью до десятых (сотых, тысячных и т.д.)» означает, что число должно содержать 1 (2, 3 и т.д.) знак после запятой. Если получившийся ответ имеет больше знаков после запятой, то его необходимо округлить до десятых (сотых, тысячных и т.д.). Задание №1. В сосуде, из которого быстро откачивают воздух, находится вода массой m г при температуре t = 0°C. В результате интенсивного испарения происходит замораживание воды. Какая часть (в %) первоначальной массы воды обратилась в лед? Ответом является целое число, при необходимости округлите ответ до целых. Ответ №1. 87 Решение №1. Энергия, необходимая для образования пара, может быть получена за счет энергии, выделившейся при замораживании воды. Пусть m1 — масса образовавшегося льда, а m2 - масса пара, тогда масса воды до замерзания m = m1 + m2 . При кристаллизации воды массой m1 выделяется количество теплоты, равное m1 . Для испарения воды массой m2 требуется количество теплоты, равное r m2 . В соответствии с законом сохранения энергии можно записать: m1 .= r m2 . m1 .= r ( m - m1 ), Откуда: m1 rm 0,87 m , что составляет 87% первоначальной r массы воды. Задание №2. Теплоёмкость некоторых материалов может зависеть от температуры. Рассмотрим брусок массы m1 1 кг, изготовленный из материала, удельная теплоёмкость которого зависит от температуры t по закону: c c1 (1 t ) , где c1 1.4 10 3 Дж/(кг C) , 0.014 C 1 . Такой брусок, нагретый до температуры t1 100 C , опускают в калориметр, в котором находится некоторая масса m2 воды при температуре t 2 20 C . После установления теплового равновесия температура в калориметре оказалась равной 1 t 0 60 C . Пренебрегая теплоёмкостью калориметра и тепловыми потерями, определите массу (в кг) m2 воды в калориметре. Известно, что удельная теплоёмкость воды c2 4.2 10 3 Дж/(кг C) . Ответ дайте с точностью до десятых. Ответ №2. 0.7 Решение №.2 Построим график зависимости удельной теплоемкости материала бруска от температуры: На оси абсцисс отмечены точки t1 , t 2 и t 0 . За время теплообмена с водой в калориметре температура бруска понизилась с t1 до t 0 . При этом брусок передал воде количество теплоты, численно равное площади заштрихованной поверхности, умноженной на массу бруска m1 1 кг. Запишем уравнение теплового баланса: 1 t1 1 t0 m2 c2 (t0 t 2 ) m1c1 (t1 t0 ) . Из этого соотношения находим: 2 m2 m1 c1 (t12 t 02 ) 2(t1 t 0 ) 0.7 кг. 2c2 t0 t2 Задание №3. При съёмке художественного фильма потребовалось заснять эпизод с падением вагонов поезда, с моста в реку. Для этого был достроен макет железной дороги, моста и вагонов в масштабе 1:50. С какой частотой кадров (в кадр/с) N1 необходимо снимать этот эпизод, чтобы при просмотре кадров со стандартной частотой N 0 24 кадра/с ситуация выглядела правдоподобно? Ответом является целое число, при необходимости округлите ответ до целых. Ответ №3. 170 Решение №3. Пусть реальный поезд падает с высоты h, тогда высота падения макета равна h/50. Обозначим через t н и t м времена падения настоящего поезда и макета. Падение и оригинала, и макета происходит с одним и тем же ускорением, равным ускорению свободного падения. Так как время свободного падения с высоты h пропорционально корню из h, то для времён t н и t м выполнено соотношение: tн h . Чтобы ситуация выглядела правдоподобно, за время падения оригинала и tм h / 50 макета должно быть отснято одинаковое количество кадров. Отсюда: N 0t н N1t м , 2 поэтому, используя предыдущее выражение, окончательно находим: N1 50 N 0 170 кадров/с. Задание №4. Автомобиль первую треть пути проехал за одну четвертую часть всего времени движения. Средняя скорость автомобиля на всем пути оказалась равной 54 км/ч. С какой скоростью (в км/ч) двигался автомобиль на втором участках пути, если на каждом участке он двигался с постоянной скоростью? Ответом является целое число, при необходимости округлите ответ до целых. Ответ №4. 48 Решение №4. S 2S S1 S 2 3 3 S 54(км / ч) vср t 3t t1 t 2 t 4 4 2S 8S 8 v2 3 54 48(км / ч) 3t 9t 9 4 Задание №5. Ледяной кубик с вмороженным в него небольшим камешком опустили в цилиндрический сосуд с водой. При этом уровень воды в сосуде повысился на 4 см, а кубик стал плавать, полностью погрузившись в воду. Во сколько раз объем камешка меньше объема льда? Плотность льда 900 кг/м3, камня - 2700 кг/м3, воды - 1000 кг/м3. Ответом является целое число, при необходимости округлите ответ до целых. Ответ №5. 17 Решение №5. Из условия плавания тел В g (V Л VК ) ( Л V Л К VК ) g 1000(V Л VК ) 900V Л 2700VК 100V Л 1700VК V Л 17VК Задание №6. На тело массы т=1кг, вначале покоившееся на горизонтальной плоскости, в течение времени t1=5с действует горизонтальная сила F=50Н. Коэффициент трения тела о плоскость μ=0.2. Ускорение свободного падения 10 м/с2. Какое расстояние (в м) пройдет тело за время движения? Ответом является целое число, при необходимости округлите ответ до целых. Ответ №6. 15000 Решение №6. Следует рассмотреть два случая: 1) F mg , тогда S 0 3 2) F mg , тогда S S1 S 2 a1t12 , а путь S 2 тело пройдет после прекращения действия силы F. S1 2 Во время действия силы ускорение равно: F mg , m a1 а после прекращения действия силы F ускорение отрицательно и равно: a2 g Максимальная скорость v max at1 как конечная скорость равна нулю. F mg t1 , тогда m 2 2a 2 S 2 v max , так 2 vmax 1 F mg t1 2a 2 m 2 g 2 S2 F mg 2 F mg 1 = t1 t1 2m m 2 g 2 S S1 S 2 t12 F mg F mg 1 2m mg S F mg F t12 2 2 m g Задание №7. На горизонтальную поверхность льда при температуре t1 = 00 С кладут однокопеечную монету, нагретую до температуры t2 = 500 С. Монета проплавляет лед и опускается в образовавшуюся лунку. На какую часть (в долях) своей толщины она погрузится в лед? Удельная теплоемкость материала монеты c = 380 Дж/ (кг · К), его плотность ρ = 8,9 г/см3. Удельная теплота плавления льда 3,4 ·105 Дж/кг, плотность льда ρл = 900 кг/м3. Ответ дайте с точностью до сотых. Ответ №7. 0.55 Решение №7. Теплота, отданная монетой при остывании Q1 cm1t Теплота, затраченная на плавление льда Q2 m л Тогда из уравнения теплового баланса можем записать: cm1t m л Пусть S - площадь одной из сторон монеты, d ее толщина, а d1 глубина лунки, тогда m1 V1 Sd 4 mл Sd1 л Подставив выражения для масс, получим cSd t Sd1 л Отношение d1 c t = 0.55 d л Задание №8. Пассажир автобуса, едущего вдоль прямого канала с водой, наблюдает за световым бликом, который отбрасывается спокойной поверхностью воды от фонаря, стоящего на противоположном берегу канала. Найдите скорость (в м/с) движения блика по поверхности воды относительно берегов канала, если высота фонаря над поверхностью воды Н=5м, высота глаз пассажира над поверхностью воды h=1.5м, скорость автобуса v=20м/с. Ответ дайте с точностью до десятых. Ответ №8. 15.4 Решение №8. Нарисуем вид канала сверху (см. рис. 1) и обозначим на нём положения автобуса, блика и столба буквами А, В и С соответственно. Пусть в момент времени t = 0 автобус находился в начале системы координат XOY — точке O, причём прямая ОС была перпендикулярна берегам канала. Тогда О А = vt. Обозначим также ОС = L, АС = l, АВ = l1, ВС = l2. Рис. 1 Рассмотрим вид сбоку в плоскости АСВ (см. рис. 2) и обозначим местонахождение глаз пассажира А1, а вершину столба С1. Так как при отражении угол А1 ВА равен углу С1 ВС, то треугольники А1 ВА и С1 ВС подобны. Поэтому Рис. 2 BC H AB h Отсюда следует, что BC BC H AC AB BC h H 5 Проведём через точку В на рисунке 4 прямую, параллельную берегам канала; она пересечёт перпендикуляр СО в точке В1. Из подобия треугольников СВВ1 и САО получаем B1C BC H OC AC H h B1C есть постоянная величина. Это означает, что точка B1 не OC меняет своего положения по координате y со временем. Таким образом, блик движется по прямой, проходящей через точку B1 параллельно берегам канала. Найдём его скорость. Длины отрезков В1 В и О А равны ut и vt соответственно. Из подобия треугольников СВВ1 и САО следует то есть отношение отношение: B1 B ut BC H OA vt AC H h из которого получается выражение для скорости блика: uv H H h Задание №9. Тягач мощностью 1000 л. с. может на ровной дороге сообщить груженой платформе скорость до 40 км/ч. Какой мощности (в л. с.) тягач нужно поставить последовательно в сцепку с имеющимся, чтобы повысить скорость перевозки платформы до 60 км/ч? Примите, что сила сопротивления пропорциональна квадрату скорости, с коэффициентом пропорциональности, одинаковым для обоих тягачей. Ответом является целое число, при необходимости округлите ответ до целых. Ответ №9. 2400 Решение №9. Движение с постоянной скоростью возможно при взаимном равенстве силы тяги, определяемой силой трения покоя между дорогой и колесами, и силой сопротивления движению: где – неизвестный коэффициент Fтр V 2 , пропорциональности в выражении силы сопротивления. Пока отсутствует проскальзывание, сила трения может быть различной (до значения mg ) и ее можно, например, выразить через мощность двигателя и скорость движения: данным для имеющегося тягача можно определить коэффициент : Сцепив два тягача, мы суммируем приложенную силу: N V 2 . V Так, по N1 N V12 31 V1 V1 . N1 N 2 V 2 . V V Теперь искомую мощность можно найти преобразованием формулы: V 3 27 8 N 2 N1 2 1 1000 2400 л. 8 V1 с. Как видим, увеличение скорости дается нелегко – такого тягача можно и не найти. 6 Задание №10. На краю крыши висят две геометрически подобные сосульки конической формы разной длины. После резкого потепления от t1 = 0 С до t2 = 10 С меньшая сосулька длины l = 10 см растаяла за время = 2 ч. За какое время 1 (в с) растает бóльшая сосулька длины L = 30 см, если внешние условия не изменятся? Ответом является целое число, при необходимости округлите ответ до целых. Ответ №10. 21600 Решение №10. Особенность этой задачи состоит в том, что энергия, необходимая для таяния льда, поступает от воздуха через поверхность сосульки, а количество льда определяется объемом сосульки. Обозначим через Р (Вт/м2) величину плотности теплового потока от воздуха к поверхности сосульки. По условию задачи за все время таяния метеоусловия не меняются. Поэтому можно предположить, что величина Р будет оставаться постоянной, ибо она в первом приближении пропорциональна разности температуры воздуха и льда. Теперь для малой сосульки можно составить уравнение теплового баланса: P S V , где S – площадь поверхности сосульки, V – ее объем, – плотность льда, – удельная теплота плавления льда. Аналогичное уравнение будет выполняться и для большой сосульки: P S1 1 V1 . Деля второе уравнение на первое, получим: S1 1 V1 S V V S . V S1 , откуда найдем время 1 : 1 1 Осталось сравнить объемы и поверхности сосулек. Из геометрии известно, что объем любого тела пропорционален третьей степени его характерного размера, площадь поверхности – квадрату характерного размера. Поэтому: V kV l 3 , V1 kV L3 , S k S l 2 , S1 k S L2 , где kV и kS – коэффициенты пропорциональности, зависящие от геометрической формы тела, но неизменные для всех геометрически подобных фигур одного типа (в данном случае для конусов). Тогда 1 kV L3 kS l 2 L 30 2 6 3 2 l 10 kV l kS L 7 ч = 21600 с.