Вариант № 2 2. A 1 № 337346. Известно, что число

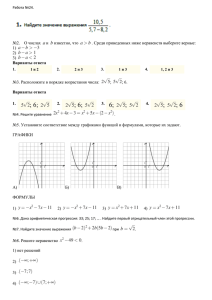
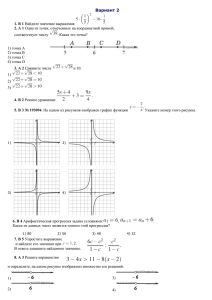
Вариант № 2
2. A 1 № 337346. Известно, что число
натами
отрицательное. На каком из рисунков точки с коорди-
расположены на координатной прямой в правильном порядке?
1) 1
2) 2
3) 3
4) 4
Решение.
Поскольку
, имеем:
Поскольку
имеем:
Правильный ответ указан под номером: 1.
3. A 2 № 337311. Между какими числами заключено число
1) 8 и 9
2) 72 и 74
3) 24 и 26
4) 4 и 5
Решение.
Сравним квадраты приведённых в условии чисел:
Число 73 лежит между числами 64 и 81, поэтому
заключено между числами 8 и 9.
Правильный ответ указан под номером 1.
4. B 2 № 338480. Решите уравнение
Решение.
Последовательно получаем:
О т в е т : −1.
5. B 3 № 339091. Установите соответствие между функциями и их графиками.
Функции
А) y = −2x + 4
Графики
Б) y = 2x − 4
В) y= 2x + 4
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
Решение.
Если прямая задана уравнением
то при
функция возрастает, при
— убывает. Значению соответсвует значение функции в точке
Уравнение
задаёт убывающую функцию, пересекающую ось ординат в точке 4.
Уравнение
задаёт возрастающую функцию, пересекающую ось ординат в точке −4.
Уравнение
задаёт возрастающую функцию, пересекающую ось ординат в точке 4.
Тем самым, искомое соответствие: А — 4, Б — 3, В — 2.
О т в е т : 432.
7. B 5 № 338092. Найдите
Решение.
Имеем:
если
О т в е т : 4.
9. B 6 № 339369.
В треугольнике ABC проведена биссектриса AL, угол ALC
равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
Решение.
Пусть угол
равен
угол
равен
Сумма углов в треугольнике
равна 180°, откуда
Аналогично, из треугольника
уравнений:
Получаем систему
Таким образом, угол
равен 62°.
О т в е т : 62.
10. B 7 № 339438.
Прямая касается окружности в точке K. Точка O —
центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла
OMK. Ответ дайте в градусах.
Решение.
Угол, образованный хордой и касательной равен половине дуги, которую он заключает, поэтому
величина дуги MK равна 2 · 83° = 166°. Угол OMK — центральный, поэтому он равен величине
дуги, на которую опирается. Значит, угол OMK равен 166°. В треугольнике OMK стороны OK и OM
равны как радиусы окружности, поэтому треугольник OMK — равнобедренный, следовательно,
углы при основании равны. Сумма углов треугольника равна 180°, поэтому
∠OKM = ∠OMK = (180° − ∠KOM)/2 = (180° − 166°)/2 = 7°.
О т в е т : 7.
11. B 8 № 340197.
В трапеции ABCD AD = 5, BC = 2, а её площадь
равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.
Проведём высоту
Средняя линия равна полусумме оснований:
Площадь трапеции равна произведению полусуммы оснований на высоту:
Поскольку
— средняя линия,
поэтому
по теореме Фаллеса получаем, что
ции
О т в е т : 11.
Отрезки
и
равны,
Найдём площадь трапе-
12. B 9 № 316348.
Решение.
Углы
и
Найдите тангенс угла, изображённого на рисунке.
в сумме образуют развёрнутый угол
Значит,
Рассмотрим прямоугольный треугольник, изображённый на рисунке. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
О т в е т : −3.
13. B 10 № 316323. Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
2) Если угол равен 120°, то смежный с ним равен 120°.
3) Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из
данной точки к прямой, больше 3.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Любые три прямые имеют не более одной общей точки» — неверно, поскольку прямые могут
совпадть и тогда точек пересечения бесконечно много.
2) «Если угол равен 120°, то смежный с ним равен 120°» — неверно, смежные углы и связаны
соотношением:
.
3) «Если расстояние от точки до прямой больше 3, то и длина любой наклонной, проведённой из
данной точки к прямой, больше 3» — верно,т. к. расстояние — длина кратчайшего отрезка до
прямой, а все наклонные — длиннее.
О т в е т : 3.
15. B 11 № 311521.
На рисунке изображен график движения автомобиля из пункта
в пункт
и автобуса из пункта
в пункт
. На сколько километров в час скорость автомобиля больше скорости автобуса?
Решение.
Автобус проехал 240 км за 5 часов. Таким образом, его скорость равна 48 км/ч. Автомобиль проехал это же расстояние за 3 часа со скоростью 80 км/ч. Таким образом, скорость автомобиля
больше скорости автобуса на 32 км/ч.
16. B 12 № 316351. На молочном заводе пакеты молока упаковываются по 12 штук в коробку,
причём в каждой коробке все пакеты одинаковые. В партии молока, отправляемой в магазин
«Уголок», коробок с полуторалитровыми пакетами молока втрое меньше, чем коробок с литровыми пакетами. Сколько литров молока в этой партии, если коробок с литровыми пакетами молока
45?
Решение.
Найдём количество коробок с полуторалитровыми пакетами молока: 45 : 3 = 15. Теперь рассчитаем количество литров молока в этой партии: 45 · 12 · 1 + 15 · 12 · 1,5 = 810 л.
О т в е т : 810.
17. B 13 № 314845.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания
флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
Решение.
Задачу можно свести к нахождению гипотенузы прямоугольного треугольника. По теореме Пифагора её длина равна
О т в е т : 17.
18. B 14 № 315142.
На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.
Какое из следующих утверждений неверно?
1) Пользователей из Украины больше, чем пользователей из Казахстана.
2) Пользователей из России вдвое больше, чем пользователей из Украины.
3) Примерно треть пользователей — не из России.
4) Пользователей из Украины и Беларуси более 3 млн человек.
Решение.
Проверим каждое утверждение:
1) Из диаграммы видно, что пользователей из Украины больше чем пользователей из "других
стран", а значит, и больше, чем пользователей из Казахстана. Первое утверждение верно.
2) Из диаграммы видно, что число пользователей из России больше, чем в два раза превышает
число пользователей из Украины. Второе утверждение неверно.
3) Из диаграммы видно, что пользователей не из России примерно треть от общего числа пользователей. Третье утверждение верно.
4) Из диаграммы видно, что пользователей из Украины и Беларуси больше, чем четверть от общего числа пользователей. Всего пользователей 12 млн, значит пользователей из Украины и Беларуси более 4 млн. Четвёртое утверждение верно.
О т в е т : 2.
19. B 15 № 316354. Фирма «Вспышка» изготавливает фонарики. Вероятность того, что случайно выбранный фонарик из партии бракованный, равна 0,02. Какова вероятность того, что два
случайно выбранных из одной партии фонарика окажутся небракованными?
Решение.
Вероятность того, что один случайно выбранный из партии фонарик — небракованный, составляет 1 − 0,02=0,98. Вероятность того, что мы выберем одновременно два небракованных фонарика
равна 0,98 · 0,98 = 0,9604.
22. C 2 № 339403. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC = 34.
Решение.
По определению параллелограмма
—
секущая при параллельных прямых, следовательно, углы
и
равны как накрест лежащие. Поскольку
треугольник
— равнобедренный, откуда
Аналогично, треугольник
— равнобедренный и
Стороны
и
равны, как противоположные стороны параллелограмма, следовательно:
О т в е т : 17.
23. C 3 № 338561. Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 11 км/ч, а вторую половину пути проехал со скоростью 66 км/ч, в
результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого
автомобилиста, если известно, что она больше 40 км/ч.
Решение.
Пусть — расстояние между A и В, км/ч — скорость первого автомобилиста, тогда
км/ч —
скорость второго автомобилиста на первой половине пути,. Первый автомобилист проделал весь
путь за часов, а второй за
часов. Время, за которое они проехали весь путь от
A до B одинаково, следовательно, можно составить уравнение:
По условию задачи скорость первого автомобилиста больше 40 км/ч, следовательно, скорость
первого автомобилиста равна 44 км/ч.
О т в е т : 44.
24. C 4 № 339602. Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.
Решение.
Проведём построения и введём обозначения как указано на рисунке. Проведём
параллельно
Поскольку
и
Фаллеса получаем, что
Следовательно,
— средняя линия. Пусть
трапеции. Площадь трапеции равна:
по теореме
— длина высоты
Откуда получаем, что
25. C 5 № 338207. Постройте график функции
ниях прямая
имеет с графиком ровно две общие точки.
Решение.
Упростим выражение:
и определите, при каких значе-
Таким образом, получили, что график нашей функции сводится к графику функции
выколотыми точками
и
Построим график функции (см. рисунок).
Этот график изображён на рисунке:
Из графика видно, что прямая
принадлежащем промежутку
Ответ:
имеет с графиком функции ровно две общие точки при
с