Õppeaine MHE0040 MASINAELEMENDID programm
реклама

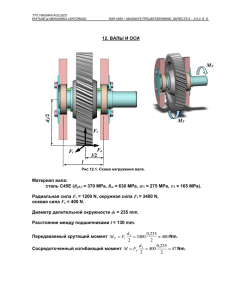
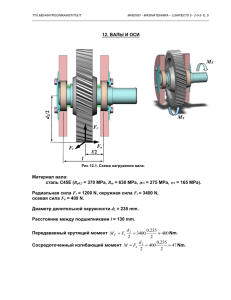
TTÜ VIRUMAA KOLLEDŽ EHITUSE ja MEHAANIKA LEKTORAAD RAR 0050 – MASINATE PROJEKTEERIMINE- 5AP/ECTS 8 - 4-0-2- E, K 15. ВИНТОВАЯ ПЕРЕДАЧА Расчитать винт и гайку ручного винтового пресса. Максимальная сила сжатия F = 25 kN и высота перемещения винта l = 400 mm. Рис 15.1. Винтовой пресс. Расчет резьбы Внутренний диаметр резьбы получим из условия прочности на сжатие где R kF eH , A S (1) k – коэффициент, учитывающий влияние крутящего момента, k = 1,25 ... 1,35; A – площадь поперечного сечения винта, A = d12/4; d1 – внутренний диаметр резьбы; ReH – предел текучести материала винта, Rp0,2 = 370 MPa (сталь C45E) S – коэффициент запаса прочности, S = 1,3 ... 4. Тогда ReH S 370 123 MPa. 3 Из уравнения (1) получим d1 4kF 4 1,3 25 10 3 0,018 m = 18 mm. 3,14 123 10 6 Выбираем трапецеидальную резьбу Tr24x5, для которой d1 = 19 mm и d2 = 21,5 mm. TTÜ VIRUMAA KOLLEDŽ EHITUSE ja MEHAANIKA LEKTORAAD RAR 0050 – MASINATE PROJEKTEERIMINE- 5AP/ECTS 8 - 4-0-2- E, K Скручивающий момент Момент, необходимый для приведения винта во вращение m T Fd 2 tan , 2 (2) – угол подъема винтовой линии, ’ – приведённый угол трения. где tan P 5 0,074 , d 2 3,14 21,5 где P – шаг резьбы. Тогда arctan 0,074 4,2 . Угол трения arctan f cos arctan 2 0,1 5,9 cos15 Для обеспечения самоторможения в резьбе необходимо, чтобы ’ > . Данное требование выполнено. Эквивалентное напряжение Из уравнения (2) получим Fd 2 25 103 0,0215 T tan tan 4,2 5,9 48 Nm. 2 2 Эквивалентное напряжение согласно III теории прочности III ekv 2 4 2 , где F 4F 4 25 10 3 88 MPa, A d12 3,14 0,019 2 (3) TTÜ VIRUMAA KOLLEDŽ EHITUSE ja MEHAANIKA LEKTORAAD RAR 0050 – MASINATE PROJEKTEERIMINE- 5AP/ECTS 8 - 4-0-2- E, K T 16T 16 48 36 MPa. W0 d 3 3,14 0,0193 1 Тогда III ekv 2 4 2 88 2 4 36 2 114 MPa 123 MPa. Проверка стабильности винта Проверку стабильности винта проведём с использованием уравнения Эйлера. Гибкость стержня i , (4) z – длина стержня, z l 0,4 m; l где z – коэффициент приведения длины, = 2; i – радиус инерции, i = d1 / 4 = 19 / 4 = 4,75 mm. Тогда z i 2 0,4 4,75 10 3 F 168 Рис 15.2. Схема нагружения. Такой гибкости соответствует коэффициент продольного изгиба 0,17. Напряжение в стержне F 4F 4 25 10 3 s 88 MPa 0,17 123 21 MPa A d12 3,14 0,019 2 Для достижения необходимой стабильности увеличим диаметр винта и примем резьбу Tr36x6, для которой d1 = 30 mm, d2 = 33 mm. Тогда радиус инерции d 30 i 1 7,5 mm, 4 4 Гибкость TTÜ VIRUMAA KOLLEDŽ EHITUSE ja MEHAANIKA LEKTORAAD z i 2 0,4 7,5 10 3 RAR 0050 – MASINATE PROJEKTEERIMINE- 5AP/ECTS 8 - 4-0-2- E, K 107 Тогда коэффициент продольного изгиба 0,37 и напряжение в стержне F 4F 4 25 10 3 s 35 MPa 0,37 123 46 MPa A d12 3,14 0,03 2 Предельное напряжение в винте kr 2E 2 3,14 2 2,1 105 107 2 181 MPa Коэффициент запаса стабильности S kr 181 5. s 35 Расчет гайки H h D1 Tr36x6 D1 Рис 15.3. Проектирование гайки. Высота гайки H zP , где (5) z – число витков резьбы. Давление на боковой поверхности витка TTÜ VIRUMAA KOLLEDŽ EHITUSE ja MEHAANIKA LEKTORAAD p F p , d 2 H1 z RAR 0050 – MASINATE PROJEKTEERIMINE- 5AP/ECTS 8 - 4-0-2- E, K (6) где H1 – рабочая высота профиля, (для трапкцеидальной резьбы H1 = 0,5P); [p] – допустимое давление, [p] = 12 MPa (для винтовой пары сталь – сталь). Тогда из уравнения (6) получим z F F 25 10 3 7,4 d 2 H 1 p d 2 0,5P p 3,14 0,03 0,5 0,006 12 10 2 Максимальное рекомендуемое число вмтков z = 10, оптимальное z = 5 ... 8. Примем z = 8. Тогда из уравнения (5) H zP 8 6 48 mm. Прочность на срез F , (7) dHkk m где k – коэффициент полноты резьбы, k 0,65; km – коэффициент неравномерности распределения нагрузки, km 0,55 ... 0,75. Тогда 25 10 3 13 MPa 0,5 0,5 123 62 MPa 3,14 0,036 0,048 0,65 0,55 Диаметр D1 получим из уравнения где Тогда A1 F 123 MPa, A1 4 D12 d 2 . 4 25 10 3 D1 d 0,036 2 0,04 m. 6 3,14 123 10 4F 2 Примем D1min = 40 mm. Диаметр D2 определим из условия прочности на смятие. TTÜ VIRUMAA KOLLEDŽ EHITUSE ja MEHAANIKA LEKTORAAD C RAR 0050 – MASINATE PROJEKTEERIMINE- 5AP/ECTS 8 - 4-0-2- E, K F C 1,7 1,7 123 209 MPa, A2 A2 где D22 D12 . 4 Тогда D2 4F C D12 4 25 10 3 0,04 2 0,042 m. 6 3,14 209 10 Конструктивно примем D2 = 45 mm. Высоту h определим из условия прочности на срез F 62 MPa. D1h Тогда F 25 10 3 h 0,003 m. D1 3,14 0,04 62 10 6 Примем hmin = 4 mm. КПД винтовой пары Угол подъёма винтовой линии arctan P 6 3,3 d 2 3,14 33 Тогда tan tan 3,3 0,36 tan tan 3,3 5,9