Определение квадратного корня. Арифметический квадратный

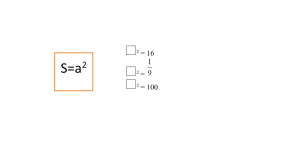
Определение квадратного корня. Арифметический квадратный корень ( 8 класс, алгебра)
I.
Актуализация
1. Устно (в виде зарядки)
- 47 Є N; - 47 Є Z; - 47 Є Q;
⅞ Є N; ⅞ Є Z; ⅞ Є Q;
19 Є N; 19 Є Z; 19 Є Q;
π Є Q; π Є R.
2. Дать определение натуральных, целых чисел.
Какие числа образуют множество действительных чисел?
Какие действительные числа можно и какие нельзя представить в
виде отношения целого числа к натуральному?
Приведите пример бесконечной десятичной дроби, которая является:
а) рациональным числом; б) иррациональным числом.
3. 52; 112; 82
II. Мотивация.
Выполним лабораторную работу:
1.
2.
3.
4.
Построить прямоугольник со сторонами 9 см и 4 см.
Построить квадрат с такой же площадью.
Построить прямоугольник со сторонами 1 см и 2 см.
Построить квадрат с такой же площадью.
Какая трудность возникла? Вы не смогли определить длину стороны нужного квадрата.
На самом деле такой квадрат построить можно. Для этого мы проведем диагональ квадрата
со стороной 1 см, а затем достроим квадрат со стороной, равной этой диагонали.
Это и будет искомая фигура. Докажем это. Проведем диагонали образовавшегося квадрата.
Четыре прямоугольных треугольника составят два квадрата со стороной 1 см. Значит их общая
площадь – это 1 см2 + 1 см2 = 2 см2. Но чему же все-таки равна сторона этого квадрата? Чтобы
разобраться в этом вопросе, мы должны изучить определение квадратного корня.
III. Изучение нового материала.
Рассмотрим уравнение х2=16. Такие уравнения нам знакомы. Очевидно, его корни 4 и -4,
т.к. 42=16 и (-4)2=16.
Определение: Квадратным корнем из числа а называется число в, квадрат которого равен
а.
Число 4 – неотрицательный корень уравнения х2=16 называется арифметическим
квадратным корнем из 16.
Определение: Арифметическим квадратным корнем из числа а называется
неотрицательное число в, квадрат которого равен а.
Знак, применяемый для обозначения операции извлечения квадратного корня, называется
радикалом. «Радикал» происходит от латинского слова «radix» - корень, «radikalis» - коренной.
Начиная с XIII века европейские математики обозначали корень этим словом или сокращенно √.
В 1525 году в книге К. Рудольфа «Быстрый и красивый сет при помощи искусных правил алгебры,
обычно называемых КОСС» появилось обозначение √ для квадратного корня. Затем над
подкоренным выражением стали писать черту. Современное обозначение корня появилось в книге
Декарта «Геометрия», изданной в 1937 году. Приближенное значение квадратных корней из целых
чисел умели находить еще в Древнем Вавилоне около 4 тыс. лет назад.
В случае с нашим квадратом сторона может быть только положительным числом. Но что
это за число, квадрат которого равен 2? Записывается так: √2. И это еще один пример
иррациональных чисел, с которыми мы познакомились на прошлом уроке. Сможете ли вы
привести пример иррациональных чисел, записываемых с помощью радикала? (ответ учся).
Из каких чисел, по-вашему, можно извлекать квадратный корень и почему? Приведите
пример выражения с радикалом, не имеющего смысла.
IV. Закрепление.
Устно: с.71 №298, №299, №301
Письменно: ( по вариантам) №300 (верхняя строка\нижняя строка) 2 ученика на скрытых
досках.
А теперь соберем и прочитаем афоризм Григория Ратнера – ЛОТО. Все вычисления
нужно записать в тетради.
«Если корни глубоки, буря не страшна»
Григорий Ратнер
(Афоризм собирается из деталей таким образом: примеры на нахождение квадратных корней
написаны на листе с различными фигурами, на каждой фигуре один пример; на вырезанных
фигурах-с одной стороны ответы, с другой-части текста. Учащиеся совмещают наложением
соответствующие ответы с примерами, таким образом, складывается афоризм)
- О каких корнях говорил Григорий Ратнер?
На повторение: №272(а), 274
Д\з: п.12, №№ 302, 304, 305
Доп. задание: №306 (устно), №314.