Интерполяция и экстраполяция

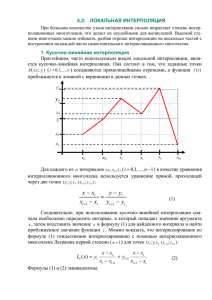
ИНТЕРПОЛЯЦИЯ И ЭКСТРАПОЛЯЦИЯ ФУНКЦИИ
Карташян Марсел Вардгесович
(ananimar@mail.ru)
Муниципальное бюджетное общеобразовательное учреждение
лицей №6 г. Шахты Ростовской области (МБОУ лицей №6 г. Шахты)
Аннотация
На занятиях по естественнонаучным предметам часто возникает
необходимость перехода от табличного способа задания функции к
аналитическому. Задача учителей математики – предоставить
простой и эффективный алгоритм (прежде всего для
вычислительных систем) для решения подставленной задачи.
Основная задача работы – краткое описание некоторых методов
интерполяции функций. В начале приводятся основные сведения об
алгебраической интерполяции. Излагаются методы линейной и
квадратичной интерполяции, а также метод Эйткена. Далее
описывается метод тригонометрической интерполяции. Работа
завершается понятием «экстраполяция функции».
 Алгебраическая интерполяция. На практике часто возникает
необходимость перехода от табличного способа задания функции к
аналитическому. Задание функции формулой имеет следующие
преимущества: во-первых, формулы занимают мало места, вовторых, как правило, с помощью формул легче выполнить
вычисления. А самое главное, с помощью таблицы невозможно
найти значения функции в тех точках, которые отсутствуют в
таблице.
Общая задача интерполяции функции заключается в том, чтобы
найти определенную на отрезке x1 ; xn функцию y  f (x) такую, что
f ( xi )  yi , где i =1, 2, …, n и x1 < x 2 <...< xn . Естественно требовать
найти простейшую функцию y  f (x) с вычислительной точки
зрения. Если простейшей назовём функцию, значения которой
вычисляются арифметическими действиями сложения, вычитания и
умножения, то такой является целая рациональная функция, то есть
многочлены.
Таким образом, одна из наиболее важных проблем состоит в том,
чтобы уметь записать многочлен Pn1 (x) степени не выше n-1,
обладающий тем свойствам, что Pn1 ( xi )  yi , i =1, 2, …, n. Очевидно,
что если такой многочлен существует, то он единственный.
Действительно, предположим, что существуют два таких
многочлена Pn1 (x) и Qn1 (x). Тогда уравнение Pn1 ( x)  Qn1 ( x)  0
степени не выше n-1 имеет n корней x i ( i =1, 2, …, n), что
невозможно. Возьмём
( x  x2 )( x  x3 )( x  x4 )...(x  xn )
y1 
( x1  x2 )( x1  x3 )( x1  x4 )...(x1  xn )
( x  x1 )( x  x3 )( x  x4 )...(x  xn )

y2  ... 
( x2  x1 )( x2  x3 )( x2  x4 )...(x2  xn )
( x  x1 )( x  x2 )( x  x3 )...(x  xn1 )
(3)

yn .
( xn  x1 )( xn  x2 )( xn  x3 )...(xn  xn1 )
Многочлены
( x  x1 )( x  x2 )...(x  xi 1 )( x  xi 1 )...(x  xn )
Li ( x) 
, i =1, 2, …, n
( xi  x1 )( xi  x2 )...(xi  xi 1 )( xi  xi 1 )...(xi  xn )
называются коэффициентами Лагранжа. Эти многочлены обладают
следующими свойствами: они имеют степень n-1, Li ( xi )  1
(i  1,2,...,n), L j ( xi )  0 при j  i.
Многочлен (3) обладает следующим свойствам: имеет степень не
выше n-1, удовлетворяет условиям P( xi )  yi , i =1, 2, …, n. Формула
(3) называется интерполяционной формулой Лагранжа, x i - узлами
интерполяции, а ( xi , y i ) – узловыми точками.
В том случае, когда функция y  P(x) на промежутке
интерполяции монотонна, в формуле (3) заменяя x на y, а y на x,
получим формулу, с помощью которой можно выполнить обратную
интерполяцию, то есть с помощью значений функции вычислить
соответствующие значения аргумента.
На практике широко применяются линейная и квадратичная
интерполяции. При n=2 интерполяционная формула Лагранжа
примет вид:
x  x2
x  x1
(4)
y  P( x) 
y1 
y2 .
x1  x2
x2  x1
В результате получается уравнение прямой, проходящей через точки
( x1 ; y1 ) и ( x2 ; y 2 ). При n=3 из формулы (3) получим формулу
( x  x2 )( x  x3 )
( x  x1 )( x  x3 )
y  P( x) 
y1 
y2 
( x1  x2 )( x1  x3 )
( x2  x1 )( x2  x3 )
( x  x1 )( x  x2 )

y 3 , которая является уравнением параболы,
( x3  x1 )( x3  x1 )
проходящей через точки ( x1 ; y1 ), ( x2 ; y 2 ) и ( x3 ; y 3 ).
Если требуется найти значение функции в точке, не являющей
узловой, то с помощью линейной интерполяцией можно
«уплотнить» таблицу не построив интерполяционный многочлен.
Пусть f ( x1 )  y1 , f ( x2 )  y 2 и f ( x3 )  y 3 , где x1  x2  x3 . Для
1
любого x  ( x1 ; x2 ) по формуле (4) получим f1, 2 ( x) 

x2  x1
P( x) 

y 2 x1  x
y 2 x2  x
, а для любого x  ( x2 ; x3 ) f 2, 3 ( x) 
y 2 x2  x
1
.
x3  x2 y 3 x3  x
f 1, 2 ( x) x1  x
1
. Такой метод
x3  x1 f 2, 3 ( x) x3  x
интерполяции называется методом Эйткена.
 Тригонометрическая интерполяция. Рассмотрим
интерполирование периодических функций. Пусть функция y  f (x)
задана на отрезке [0; 2 ] таблицей значений yi  f ( xi ) в
2i
равноотстоящих узлах xi 
, i =0,1, 2, … , n-1 или xi  x0  ih,
n 1
i =0, 1, …, n-1. Тригонометрическим многочленом степени m
m
m
называется многочлен Pm ( x)  k 0 ak coskx  k 1 bk sin kx.
Задача тригонометрической интерполяции состоит в построении
тригонометрического интерполяционного многочлена,
удовлетворяющего условиям ( )= , i=0,1, 2, …, n-1. Можно
показать, что решением этой задачи является многочлен
(x)=
+
, где коэффициенты
и
Тогда f ( x)  f 1, 2, 3 ( x) 
вычисляются по следующим формулам:
=
,
=
=
,
, k=1, 2, …, m.
 Экстраполяция функции. Экстраполяция – приближённое
определение значений функции в точках, лежащих вне отрезка
x1 ; xn (см. алгебраическая интерполяция). Методы экстраполяции в
основном совпадают с методами интерполяции. Например, значения
функции можно вычислить с помощью того же интерполяционного
многочлена.
По описанным выше алгоритмам можно составить компьютерные
программы нахождения приближённых значений функции, заданной
таблицей. Автором строк составлены программы, применяемые
алгебраической (метод выбирается пользователем) и
тригонометрической интерполяцией. Программы можно найти в
использованных источниках или спросить по электронному адресу.
Использованные источники
Ракитин В. И., Первушин В. Е. Практическое руководство по
методам вычислений с приложением программ для персональных
компьютеров. – М.: «Высшая школа», 1998 г.
Ханова А. А. Интерполяция функций. – Астрахань: Институт
информационных технологий и коммуникаций, 2001 г.
Ващенко Г. В. Вычислительная математика: основы
алгебраической и тригонометрической интерполяции. – Красноярск:
СибГТУ, 2008 г.