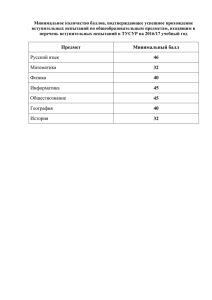
Задача 1. Методом изоклин построить интегральные кривые уравнения.
𝑑𝑦
= 2𝑥(1 − 𝑦)
𝑑𝑥
Решение
Для построения интегральных кривых уравнения
𝑑𝑦
изоклин,
конкретных
необходимо
рассмотреть
несколько
𝑑𝑥
= 2𝑥(1 − 𝑦) методом
значений
производной, которые определяют наклон касательных к интегральным
кривым. Изоклины — это кривые, вдоль которых производная сохраняет
постоянное значение. В данном случае, изоклины будут определяться
уравнением 2𝑥(1 − 𝑦) = 𝐶, где С - константа, соответствующая значению
производной.
Для C = 0
𝑥 = 0
или 𝑦 = 1
Для C = 1
𝑦 =1−
1
2𝑥
𝑦 =1+
1
2𝑥
Для C = -1
Для C = 2
𝑦 = 1−
1
𝑥
Задача 2. Решить уравнение, допускающее понижение порядка.
𝑥 2 𝑦 ′′ = 𝑦 ′2
Решение
𝑥 2 𝑦 ′′ = 𝑦 ′2
𝑝(𝑥) = 𝑦 ′ (𝑥)
𝑦 ′′ (𝑥) = 𝑝′ (𝑥) ⋅ 𝑝(𝑥)
𝑥 2 𝑝′ (𝑥) ⋅ 𝑝(𝑥) = 𝑝2 (𝑥)
𝑝′ (𝑥) =
𝑝(𝑥)
𝑥2
𝑑𝑝 𝑑𝑥
= 2
𝑝
𝑥
∫
𝑑𝑝
𝑑𝑥
=∫ 2
𝑝
𝑥
1
ln|𝑝| = − + 𝐶1
𝑥
1
𝑝 = 𝐶2 𝑒 −𝑥
1
𝑦 ′ (𝑥) = 𝐶2 𝑒 −𝑥
1
𝑦(𝑥) = 𝐶2 ∫ 𝑒 −𝑥 𝑑𝑥
2
Задача 3. Решить систему уравнений
𝑑𝑥 𝑡
=
𝑑𝑡 𝑦
𝑑𝑦
𝑡
=
−
{ 𝑑𝑡
𝑥
Решение
𝑑𝑥 𝑡
=
𝑑𝑡 𝑦
𝑑𝑦
𝑡
=
−
{ 𝑑𝑡
𝑥
𝑡
𝑑𝑥 = 𝑑𝑡
𝑦
{
𝑡
𝑑𝑦 = − 𝑑𝑡
𝑥
𝑑𝑥
𝑑𝑦
=
𝑡/𝑦 −𝑡/𝑥
𝑥 𝑑𝑥 = −𝑦 𝑑𝑦
∫ 𝑥 𝑑𝑥 = − ∫ 𝑦 𝑑𝑦
𝑥2
𝑦2
=− +𝐶
2
2
𝑥2 + 𝑦2 = 𝐶
Задача 4. Вероятность появления события в каждом испытании равна 0,7.
Сколько нужно провести испытаний, чтобы наивероятнейшее число
появлений события равнялось 10?
Чтобы найти наивероятнейшее число появлений события, мы можем
использовать формулу для биномиального распределения. В биномиальном
распределении, наиболее вероятное число успехов k в n испытаниях можно
3
приблизительно найти, используя формулу 𝑛 ∗ 𝑝, где p – вероятность успеха
в каждом испытании.
𝑛𝑝 = 𝑘
𝑛 × 0.7 = 10
𝑛=
10
0.7
Чтобы наивероятнейшее число появлений события было равно 10 при
вероятности
0,7,
необходимо
провести
примерно
14,29
испытаний.
Поскольку количество испытаний должно быть целым числом, мы можем
округлить это значение до 15 испытаний.
4