16 Оптимизация из ЕГЭ прошлых лет 2n0ai

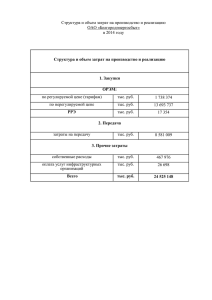
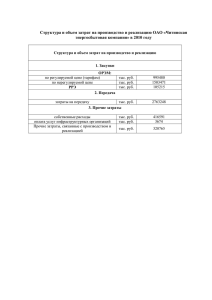
o
v
o
k
l
o
k
sh
o
k
l
o
v
e
lk
e
n
o
n
i
k
l
k
li
h
n
h
n
s
s лет. Оптимизация
o
o
.
.
№15
из
ЕГЭ
прошлых
o
v
vo
o
o
k
e
e
l
lk
n
n
№1
o
i
o
kравна t тысяч рублейnвlконце кажli стоимость которых
k фонд владеет акциями,
h
n
h
Пенсионный
s
o
s
o
.
.
o
дого года t (t = 1; 2; . . . ). Фонд
года и положить
o может продать все акции в конце некоторого
v
v
o
o
все вырученные с продажи
средства на счет в банке.
Известно, что тогда
kв конце каждого сле-ne
k
e
l
e
l
n
o
n
i
o увеличивать сумму,liнаходящую на счете, hнаk20%. В конце какого года
дующего года банк будет
l
i
k
l
n
n к концу 30-го года была
s максимальной? .o
sh акции, чтобы прибыль
o
on фонд должен продать
.
o
o
v
v
Ответ
o
o
k
k
e
l
e
l
В конце
11-ого
года
n
o
n
o
i
i
k
l
k
l
n
n
n
Решение
sh
o
sh
o
o
.
.
.
o на 20%, то есть в 1,2 раза. Если же фонд всеovo
o Каждый год банк увеличивает сумму на счету
v
v
o увеличивается в e
o еще держит акции,eто их цена после t-ого года
k
k
l
k
l
l
n
o
n
i
o
i
k
l
o
k
l
h
n
h
1
t
+
1
(t
+
1)
n
s
s= t = 1 + t .oраз
.o
t
o
o
v
v
o
o коэффициент уменьшается
k
k
l
k
Этот
с ростом t. Значит,
если при каком-то t онeстал меньше 1,2,
e
l
l
n
o
n начиная с (t + 1)-ого,
o вклад в банке будет lприносить
i
oв каждый следующийliгод,
k
то
большую hk
k
n
h
n
h
s
s будут приносить большую
o
s прибыль. В то же время
o
.
до (t + 1)-ого года акции
прибыль.
.
o найти такое значение t, при котором ovo
v
Значит, нам нужно
o
k
e
k
e
l
l
n
n
o
i
o
l
l(ti +t 1) ⩽ 1,2 < (t −t 1)shk
k
n
n
h
s
.o
.o
o
o
vчем в 1,2 раза, но
v год, после которого акции вырастут больше
То есть нужно найти такой
o
o
k
e
k чем в 1,2 раза. ne
l
e
l
после следующего — меньше
n
o
n
i
o
l
k
li
li Заметим, что shk
n
h
n
n
s
o
.
11 .o121
.o
o
o= 100 = 1,21 > 1,2
v
10v
o
o
k
l
l·k1,2 = 145,2 > 144. ine
o
ne 1112 < 1,2, так как 121
o
Но lуже
i
k
l
k
n
h
n
h
n
s
o
s
o
o
.
.
. Таким образом,
o
o
o
v
v
v
o
o
12 ko
11
k
e
l
k
e
l
<
1,2 <
l
n
o
n
o
11
10
i
i
k
l
k
l
ko
n
n нужно продать в конце
Значит, акции
sh
sh 11-ого года.
o
o
.
.
o
o
v
v
o
o
k
e
k
e
l
l
n
o
n
o
i
o
i
k
l
k
l
k
n
n
sh
sh
o
sh
o
.
.
o
o
v
v
o
o
k
e
k
e
l
e
l
n
n
o
i
o
l
k
li
k
n
h
n
h
s
s
.o
.o
o
o
v
v
o
o
1
k
e
k
e
l
e
l
n
n
o
n
i
o
l
k
li
k
li
n
h
n
h
n
s
s
o
.o
.o
2
2
2
2
2
2
%deb88fb19dbfae2c2d57c01b9d4b5dfa%
2
2
2
2
2
2
2
2
2
2
2
o
v
o
k
l
o
k
sh
o
k
l
o
v
e
lk
e
n
o
n
i
k
l
k
li
h
n
h
n
s
s
o
o
.
.
№2
o
voнового завода стоит 340 млн рублей. Затратыkoнаv производство x тыс.eединиц
Строительство
o
e + x + 12 млн рублейoвl год.
lk
n
n
продукции o
на таком заводе равны i0,3x
i
l
k
l
k
n фирмы (в
h за единицу, то прибыль
n
Если
по цене p тыс. рублей
s
o
shпродукцию завода продать
o
.
o
o. px − (0,3x + x + 12) . Когда завод будетovпостроен,
млн рублей) за один год составит
каждый
v
o
k прибыль была наи-ne
год фирма будет выпускать
продукцию в такомeколичестве, чтобы годовая
k
l
e
l
n
o
n
i
o
i
l
i
k
большей.
l
k
l
n
h
n
h
s рублей за единицу..Кажo
o
В первый годsпосле постройки завода
цена продукции p = 14 тыс.
on
.
o
o
vсколько
дый следующий год цена продукцииv увеличивается на 1 тыс. рублей за единицу. За
o
o
k
k
e
l
e
лет окупится
строительство завода?
l
n
o
n
o
i
k
l
k
li
n
h
n
h
Ответ
n
s
o
s
o
o
.
.
.
o
o
o 3
v
v
v
o
o
o Решение e
k
k
e
l
k
l
l
o
n (в млн рублей) за один
o год составит lin
o
i
k
k
Прибыль фирмы
l
h
n
h
n
s
s
o
o
.
px − 0,3x + x + 12 o
o.
v
v
o
o
k
k
e
l
k
e
Найдем
x, при котором годовая
прибыль будет наибольшей
при цене p тыс.
рублей за едиl
l
n
o
n
o
i
o продукции.
i
k
l
k
l
k
ницу
h
n
h
n
h
s
s
s Рассмотрим функцию
.o
.o
o
o
v f (x) = px − 0,3x + x + 12 = −0,3x + x(pk−ov1) − 12
o
e
e
l
lk
n
n
o
i
o
l
kзначения при
liдостигает наибольшего
k
Это квадратичная
функция, она
n
h
n
h
s
.o
.o x = x = p − 1 s
o
o
v
v
0,6
o
o
k
e
k
e
l
e
l
n
Далее имеем:
n
o
n
i
o
i
l
k
l
k
li
p − 1
n
h
n
h
n
p−1
(p −s1)
o
sf (x ) = −0,3
.
+o
(p − 1) − 12 =
− 12
.
.o
o
0,6 o
1,2
v
v 0,6
o
o
k
Прибыль
фирмы
(в
млн
рублей)
при
цене
p
=
14
тыс.
рублей
за
единицу
продукции
за
k
e
l
e
l
n
o
n
o
k
первыйliгод составит
li5
k (14 − 1)
n
h
n
h
n
s
o
s
o
o
.
− 12 .= 128
.
o
o 6
1,2
o
v
v
v
op = 15 тыс. рублей eза единицу продукции заlko
o Прибыль фирмыe (в млн рублей) при цене
k
k
l
l
n
o
n
o
i
i
k
l
k
l
ko второй год составит
n
(15
sh
sh− 1) − 12 = 151 1 .on
o
.
1,2
3 o
o
v
v
o
o
Прибыль
за 2 года меньне 340 млн рублей.
k
e продукции за o
e
l
lk
n
n
o
Прибыль фирмы (в млн
рублей)
при
цене
p
=
16
тыс.
рублей
за
единицу
i
o
k
l
k
k год составит nli
h
n
h
h
s
второй
s
s
.o
.o
(16 − 1)
1
o
o
v
− 12 = 175
v
o
1,2
2
o
k
e за 3
k
e
l
e
lприбыль
n
n
Суммарная
за 3 года больше
340
млн
рублей.
Строительство
завода
окупится
o
i
o
l
k
li
k
n
h
n
h
года.
s
s
.o
.o
o
o
v
v
o
o
2
k
e
k
e
l
e
l
n
n
o
n
i
o
l
k
li
k
li
n
h
n
h
n
s
s
o
.o
.o
2
2
2
2
%deb88fb19dbfae2c2d57c01b9d4b5dfa%
2
0
2
2
0
2
2
2
o
v
o
k
l
o
k
sh
o
k
l
o
v
e
lk
e
n
o
n
i
k
l
k
li
h
n
h
n
s
s
o
o
.
.
№3
o
vxo единиц продукции обходится в q = x + 6xk+ov10 рублей в месяц. При
Производство
цене
o
e
k
e
l
l
n
n от продажи этой
o продукции составляетli 500x − q
500 рублейoза единицу месячная прибыль
i
k
l
k
n
h
n
рублей.sh
Сколько единиц продукции
нужно ежемесячно выпускать
для полученияoмаксимальной
s
o
.
o
o.
прибыли?
v
v
o
o
k
e
k
e
l
e
Ответ
l
n
n
o
n
i
l
k
li
ko
li 247
n
h
n
h
n
s
o
s
o
o
.
.
o
Решение
o
v
v
o
o
Подставим стоимость производства
x
единиц
продукции
q
в
формулу
прибыли:
k
k
e
l
e
l
n
o
n
o
i
kq = 500x − x − 6x − 10n=l −x + 494x − 10 shk
li
n
h
500xs−
n
o
o
o
.
.
.
o
o в максимуме функции
o Очевидно, что максимальная прибыль достигается
v
v
v
o
o
o
k
k
e
l
k
e
l
l
o
n
o −x + 494x − 10 lin
o
i
k
k
l
f (x)
=
h
n
h
n
s
s
o
o
.
o. это квадратичная функция, то ее графикov—oпарабола с ветвями вниз, так как
Так vкак
o перед x отрицательный.
k
k
e
l
коэффициент
k
e
l
l
n
o
o
i способами. hk
oПри этом значение x, lвinкотором достигаетсяhмаксимум,
l
k
можно найтиnдвумя
k
n
s
s
o
sh Способ 1.
o
.
.
o
o находится по формуле
v
v
Вершина параболы
o
o
k
e
k
e
l
l
n
n
o
i
o
b
494
i
l
k
k
xl= − = −
= 247
n
h
n
h
2a
2
·
(−1)
s
s
.o
.o
o
o
v
v
Способ 2.
o
o
k
e
e
l
e
Найдем производнуюlk
n
n
o
n
i
o
i
l
k
k
li
f (x)n
=l −2x + 494
n
h
h
n
s
o
s
o
.
.
.o
o
В точке экстремума производная равна
v
vo нулю, значит искомый x будет решениемkуравнения
o
o
l
e
lk + 494 = 0, x = 494in=e247
o
n
o
−2x
i
k
k
l
2l
n
h
n
h
n
s
o
s
o
o
.
.
.
o
o
o
v
v
v
o
o
o
k
k
e
l
k
e
l
l
n
o
n
o
i
i
k
l
k
l
ko
n
n
sh
sh
o
o
.
.
o
o
v
v
o
o
k
e
k
e
l
l
n
o
n
o
i
o
i
k
l
k
l
k
n
n
sh
sh
o
sh
o
.
.
o
o
v
v
o
o
k
e
k
e
l
e
l
n
n
o
i
o
l
k
li
k
n
h
n
h
s
s
.o
.o
o
o
v
v
o
o
3
k
e
k
e
l
e
l
n
n
o
n
i
o
l
k
li
k
li
n
h
n
h
n
s
s
o
.o
.o
2
2
2
2
%deb88fb19dbfae2c2d57c01b9d4b5dfa%
2
′
o
v
o
k
l
o
k
sh
o
k
l
o
v
e
lk
e
n
o
n
i
k
l
k
li
h
n
h
n
s
s
o
o
.
.
№4
o
v на производство тыс. ед.
voнового завода стоит 159 млн рублей. Затраты
o
Строительство
o
k
e завода
e
l в год. Если продукцию
lk
n
o
продукции oна таком заводе равныin
0,5x + 2x + 6 млн рублей
i
l
k
l
k
n
h
n
h
продать
o за один год
s по цене тыс. рублей.oза единицу, то прибыльs фирмы (в млн рублей)
.
o
o. Когда завод будет построен, фирма будет выпускать
составит px − (0,5x + 2x +v6)
v продукцию
o
o
k год p = 10, а далееne
в таком количестве, чтобы
прибыль была наибольшей.
При этом в первый
k
e
l
e
l
n
o
n
i
o на 1. За сколько летliокупится строительство?
l
i
k
каждый год возрастает
k
l
n
h
n
s
o
sh
o
on
.
.
Ответ
o
v
vo
за 4 года
o
o
k
k
e
l
e
l
n
o
n
o
i
Решение
k
l
li такое количествоshkпроизводимой продукции
n
h
n
n
s
o
Найдем
x,
при
котором
прибыль
фирмы будет
o
o
.
.
.
o нужно найти максимум выражения px −ovo
oнаибольшей при фиксированном p. Для этогоovнам
v
o (0,5x + 2x + 6) . e
k
k
e
l
k
l
l
n
o
n px − 0,5x + 2x +k6o = −0,5x + (p − 2)x −li6 =
o
i
k
l
h
n
h
n
s
s
.o
= −0,5 x − 2(p − 2)x + 12 =
.o
o
o
v
v
= −0,5 x − 2(p − 2)x + (p − 2) o
− (p − 2) + 12 =
o
k
k
e
l
k
e
l
l
n
o
n − p + 2) + 0,5(p −k2)o − 6
i
o
= −0,5(x
i
k
l
l
k
h
n
h
n
h
s
s Заметим, что −0,5(x
.o
.o − p + 2) ⩽ 0, поэтомуs
o
o
v
v
o
o
k
e
−0,5(x
−
p
+
2)
+
0,5(p
−
2)
−
6
⩽
0,5(p
−
2)
−6
e
l
lk
n
n
o
i
o
i
l
k
l
k
n
h
n
h
Значит,
s + 2x + 6) равно 0,5(p
o − 2) − 6 и
s максимальное значение
o выражения px − (0,5x
.
.
o
o
достигается при
v
v
o
o
k
e
x
−
p
+
2
=
0
⇒
x
=
p
−
2
k
e
l
e
l
n
n
o
n
i
o
l
k
li
k год фирма будет зарабатывать
li То есть за каждый
0,5(p − 2) − 6hмлн рублей.
n
n
h
n
s
.o за этот год составитs 0,5(10 − 2) − 6 = 26vo<.o159
.o
В первый год p = 10. Тогда прибыльoфирмы
v
o
млн рублей.
o
k
k
e
l
e
l
Прибыль
n фирмы за второй kгодo составит 0,5(11 − 2) l−in6 = 34, 5 млн рублей,hkтакo как p = 11.
i
l
n
n = 60,5 < 159 млн рублей.
h заработает 26 +.34,5
n
Значит,
за первые два года s
фирма
s
o
o
o
.
. Прибыль фирмы за третий год — 0,5(12 − 2)vo− 6 = 44 млн рублей, так как p = 12. Значит, vo
o
vза первые три года фирма заработает 60,5 +k44o = 104,5 млн рублей. e
o
o
k
l
k
e
l
l
n так как p = 13. Всего
o
n за четвертый год — 0,5(13−2)
o
i
i
Прибыль фирмы
−6 = 54,5 млнlрублей,
k
k
l
ko
nрублей. Значит, строительство
n года фирма заработает
sh
sh 104,5 + 54,5 = 159 млн
o
за первые четыре
o
.
.
o
o 4 года.
окупитсяvза
v
o
o
k
e
k
e
l
l
n
o
n
o
i
o
i
k
l
k
l
k
n
n
sh
sh
o
sh
o
.
.
o
o
v
v
o
o
k
e
k
e
l
e
l
n
n
o
i
o
l
k
li
k
n
h
n
h
s
s
.o
.o
o
o
v
v
o
o
4
k
e
k
e
l
e
l
n
n
o
n
i
o
l
k
li
k
li
n
h
n
h
n
s
s
o
.o
.o
2
2
2
2
2
2
2
2
2
2
2
2
2
2
%deb88fb19dbfae2c2d57c01b9d4b5dfa%
2
2
2
2
2
2
2
2
o
v
o
k
l
o
k
sh
o
k
l
o
v
e
lk
e
n
o
n
i
k
l
k
li
h
n
h
n
s
s
o
o
.
.
№5
o
v на обслуживание x тысяч
voнового аквапарка стоит 40 млн рублей. Затраты
o
Строительство
o
k
e P тыс.
eмлн рублей в год. Еслиolбилеты продавать по цене
lk
n
n
посетителейoсоставляют x + 5x + i3,5
i
l
k
l
k
n
h
n
h
x
+
5x
+
3,5
.
рублейsза штуку, то прибыль аквапарка
в
млн
рублей
за
один
год
составит
P
x−
s
o
o
.
.
o
o он будет принимать посетителей в такомovколичестве, чтобы
Когда аквапарк будет построен,
v
o
прибыль была наибольшей
(желающих будет предостаточно).
При какомlkнаименьшем значении e
k
e
e
l
n
n
n
i
o окупится не болееli чем за 4 года? hko
l
i
P строительство аквапарка
k
l
n
n
h
s
o
s
o
on
.
.
Ответ
o
o
v
v
11
o
o
k
k
e
l
e
l
n
o
n
o
i
Решение
i
k
l
k
l
n не более чем за 4shгода, то прибыль .on
h
n как строительство sаквапарка
Так
должно окупиться
o
o
.
.
o То есть цена P должна быть такой, чтобыovo
oза 4 года должна составить не менее 40 млнoруб.
v
v
o существовало какое-нибудь
k
k
e
решение неравенства
l
k
e
l
l
n
o
n o
k
ko
li
li
h
n
h
2
2
n
s
.o4 P x − 3 x + 5x + 3,5s ⩾ 40 ⇔ P x v−o.o3 x + 5x + 3,5 ⩾ 10
o
v
2
2 o
o
k
− x + (P −
5)x − 3,5 ⩾ 10 ⇔ lk
x − (P − 5)x + 13,5 ⩽ 0 e
l
k
e
l
n
3
3
o
n
o
i
o
i
k
l
k
l
k
h
n
h
n
h
s
График
левой
части
последнего
неравенства
при
всяком
фиксированном
P
представляет
s
o
s
o
.
.
o
o
собой параболу с ветвями,
направленными вверх. Тогда у последнего
v неравенства есть решение
v
o
o
k лежит не выше осиneOx, то
тогда и только
kтогда, когда вершинаneсоответствующей параболы
l
l
o
i
o
i
l
есть y ⩽ 0k:
k
l
n
h
n
2
sh
.o
· 0,75(P.o− 5) − (P − 5) · 0,75(Ps− 5) + 13,5 ⩽ 0
o
3
o
v
v
o
o
Это равносильно
k
e
k 3
e
l
e
l
n
n
o
n
i
o
l
k 8 (P − 5) ⩾ 13,5nli ⇔ (P − 5) ⩾ 36 shk
li
n
h
n
o
s
o
.
.
Отсюда с учётом условия P > 0 получим
P ⩾ 11.
.o
o
o при которой аквапарк имеет шанс окупиться
v за
vбилета,
Таким образом, минимальная цена
o
o
k
k
e
lP = 11 тыс.
e наличии достаточногоolколичества
4 года (при
желающихin
его посетить), составляет
o
n
i
k
l
k
l
n
h
n
рублей.
h
n
s
o
s
o
o
.
.
.
o
o
o
v
v
v
o
o
o
k
k
e
l
k
e
l
l
n
o
n
o
i
i
k
l
k
l
ko
n
n
sh
sh
o
o
.
.
o
o
v
v
o
o
k
e
k
e
l
l
n
o
n
o
i
o
i
k
l
k
l
k
n
n
sh
sh
o
sh
o
.
.
o
o
v
v
o
o
k
e
k
e
l
e
l
n
n
o
i
o
l
k
li
k
n
h
n
h
s
s
.o
.o
o
o
v
v
o
o
5
k
e
k
e
l
e
l
n
n
o
n
i
o
l
k
li
k
li
n
h
n
h
n
s
s
o
.o
.o
2 2
3
2 2
3
2
2
2
%deb88fb19dbfae2c2d57c01b9d4b5dfa%
2
в
2
2
2
o
v
o
k
l
o
k
sh
o
k
l
o
v
%deb88fb19dbfae2c2d57c01b9d4b5dfa%
e
lk
e
n
o
n
i
k
l
k
li
h
n
h
n
s
s
o
o
.
.
№6
o
v составила x% годовых, а в
voгода процентная ставка по депозитам в банке
o
В январе 2014
o
k
e года
e
l
lk
n
n
o
январе 2015o года — y% годовых. Вкладчик
положил
на
счет
в
этом
банке
в
январе
2014
i
i
l
k
l
k
n
h
n
h
некоторую
В январе 2015 года, спустя
s год после открытия.oсчета, он снял
s сумму денег в рублях.
o
.
o значение x, при
o суммы, которую положил в 2014 году. Найдите
со счета пятую часть от той
v
v
o что x + y = 30. e
k
котором сумма на счете
вoянваре 2016 года будет
наибольшей, если известно,
k
e
l
e
l
n
n
o
n Ответ
i
o
i
l
i
k
l
k
l
n
h
n
h
s
o
s
o
on
.
25
o
o.
v
v
o
o
Решение
k
k
e
l
e
l
n год, то есть в 2015koгоду, на счете
n вкладчик положил kнаoсчет A рублей. Тогда lспустя
i
Пусть
i
l
n
n
nбудет в рублях
sh
o
уже
sh
o
o
.
.
.
o
o
o
(1 + 0,v01x)A
v
v
o
o
o
k
k
e
l
1
k
e
l
l
n в рублях
o
на счете осталось
Затем вкладчик
n снял со счета 5 A, следовательно,
o
i
o
i
k
l
k
l
h
n
h
n
s
s
o
o
.
1
o.
(1 + 0, 01x)A − Avo
v
5o
o
k
k
e
l
k
e
l
l
n
o
n на счете будет суммаkвoрублях:
i
oТогда в январе 2016 года
i
k
l
l
k
h
n
h
n
h
s
s
s
1 .o
.o
(1 + 0, 01y) (1 + 0, 01x)A − A =
o
o
v
5
v
o
o
k
e
e
= (1 + 0,
01y)(1 + 0, 01x − 0, 2)Al
lk
n
n
o
i
o
l
k
k по условию y = 30 −nxliи рассмотрим функцию
n
h
h
Выразим
s
s
.o
.o
o
o
v = (1 + 0, 01(30 − x))(1 + 0, 01x − 0, 2) = kov
fo(x)
e
k
e
l
e
l
n
1
n
o
n
i
o
i 50x + 130 · 80) hk
l
=
· (−x l+
k
li
n
10
n
h
n
s
o
s
o
.
.
.o
o
o
Графиком этой функции является vпарабола,
ветви которой направлены вниз. Следовательv
o
o
но, наибольшее
значение
она
принимает
в
вершине
k
e
l
e
lk
n
o
n
o
i
i
k
l
k
l
−50
n
h
n
h
n
s
x
=
=
25
o
s
o
o
.
−2 .
.
o
o
o
v
v
v
o
o в январе 2016 года будет
сумма на счете
при x = 25.
o Таким образом, наибольшая
k
k
e
l
k
e
l
l
n
o
n
o
i
i
k
l
k
l
ko
n
n
sh
sh
o
o
.
.
o
o
v
v
o
o
k
e
k
e
l
l
n
o
n
o
i
o
i
k
l
k
l
k
n
n
sh
sh
o
sh
o
.
.
o
o
v
v
o
o
k
e
k
e
l
e
l
n
n
o
i
o
l
k
li
k
n
h
n
h
s
s
.o
.o
o
o
v
v
o
o
6
k
e
k
e
l
e
l
n
n
o
n
i
o
l
k
li
k
li
n
h
n
h
n
s
s
o
.o
.o
2
4
0