Теплообменные устройства энергетических установок космических аппаратов

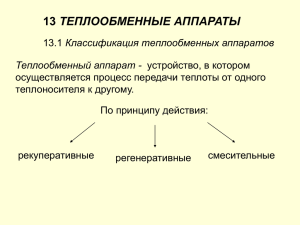
В.В. ХОДОСОВ
ТЕПЛООБМЕННЫЕ
УСТРОЙСТВА
ЭНЕРГЕТИЧЕСКИХ
УСТАНОВОК
КОСМИЧЕСКИХ
АППАРАТОВ
Министерство образования и науки Российской Федерации
Балтийский государственный технический университет «Военмех»
Кафедра «Космические летательные аппараты и двигатели»
В.В. ХОДОСОВ
ТЕПЛООБМЕННЫЕ
УСТРОЙСТВА
ЭНЕРГЕТИЧЕСКИХ
УСТАНОВОК КОСМИЧЕСКИХ
АППАРАТОВ
Учебное пособие
Санкт-Петербург
2018
УДК 629.78.064.5(075.8)
Х69
Х69
Ходосов, В.В.
Теплообменные устройства энергетических установок космических аппаратов: учебное пособие / В.В. Ходосов; Балт. гос. техн.
ун-т. – СПб., 2018. – 25 с.
Описываются состав и основные характеристики
теплопередающих и теплоотводящих устройств энергетических установок космических аппаратов, физические принципы их устройства и функционирования
и конструктивные особенности. Особое внимание
уделено расчёту проектных параметров и выбору конструктивных схем. Изложение теории сопровождается
конкретными практическими примерами.
Предназначено для студентов и аспирантов вузов, готовящих специалистов в области ракетнокосмической техники и энергетических систем.
УДК 629.78.064.5(075.8)
Р е ц е н з е н т канд. техн. наук, доц. А.С. Павлов
Утверждено
редакционно-издательским
советом университета
 В.В. Ходосов, 2018
 БГТУ, 2018
1. ОБЩИЕ СВЕДЕНИЯ О ТЕПЛООБМЕННЫХ УСТРОЙСТВАХ
ЭНЕРГЕТИЧЕСКИХ УСТАНОВОК
1.1. Теплообменные аппараты
Повышение КПД машинных преобразователей энергии возможно
за счёт регенерации тепловой энергии – передачи теплоты от более
нагретого теплоносителя к менее нагретому. Эту задачу выполняют
теплообменные аппараты, которые по принципу действия могут быть
разделены на контактные и поверхностные. В контактных теплота
передаётся в результате непосредственного контакта (смешения) двух
теплоносителей. Поверхностные разделяют на рекуперативные и регенеративные. В рекуперативных теплота передаётся от одного теплоносителя к другому через разделяющую их твёрдую стенку, в регенеративных стенка находится попеременно в контакте то с горячим,
то с холодным теплоносителем. В космических энергетических установках используются поверхностные теплообменные аппараты, в газотурбинных и паротурбинных установках (ГТУ и ПТУ) – рекуператоры, в двигателях Стирлинга – регенераторы.
Целью расчёта теплообменного аппарата является определение
площади поверхности (а следовательно, и массы) теплообмена и
энергетических затрат на прокачку теплоносителей. Расчёты основаны на совместном решении уравнения теплового баланса и уравнения
теплопередачи. Процесс теплопередачи в рекуператоре является стационарным, а в регенераторе – нестационарным.
По сравнению с системой обеспечения теплового режима КА в
энергетических установках теплообменные аппараты передают существенно большие тепловые потоки при высокой температуре теплоносителя. Так, в ГТУ с полезной мощностью 3 кВт рекуператор должен
обеспечить тепловую мощность ≈13 кВт. Это позволяет повысить
КПД с 23% для ГТУ без регенерации до 30%.
1.1.1. Рекуператор
Простейшим рекуператором является аппарат типа “ труба в трубе” (рис. 1.1), в котором могут быть реализованы две схемы движения
теплоносителей: прямоток и противоток. На рис. 1.2 показаны изменения температуры греющего и нагреваемого теплоносителей по
длине рекуператора. В ПТУ процесс теплопередачи может протекать
при конденсации греющего теплоносителя. В этом случае его температура будет постоянна по длине рекуператора.
3
t1’’
Газ2
t2’
t1’
t2’’
ТЗП
Газ1
Рис. 1.1. Схема простейшего рекуператора типа «труба в трубе»
прямоток
t2
противоток
’
t2 ’
t2’’
t2’’
t1’’
t1 ’
t1’’
t1 ’
Рис. 1.2. Изменения температуры греющего и нагреваемого теплоносителей
по длине рекуператора
Из уравнения теплопередачи можно найти тепловой поток от
греющего теплоносителя к нагреваемому:
Q = h ⋅ ∆tср ⋅ A,
(1.1)
1
коэффициент теплопередачи; ∆tср – средняя раз1 δ 1
+ +
α1 λ α 2
ность температур греющего и нагреваемого теплоносителей; A – площадь поверхности нагрева, м2.
При проектировании рекуператора должны быть известны расход
теплоносителей, их температуры t1′, t1′′, t 2′ , t 2′′ и теплоёмкости. Искомая
величина – поверхность нагрева. Массовый расход
где h =
4
G =W ⋅ S ⋅ρ ,
(1.2)
где W – средняя скорость, м/с; S – площадь поперечного сечения, м2;
ρ – плотность газа, кг/м3.
Для ГТУ и ПТУ массовые расходы нагреваемого и греющего
теплоносителей G1 и G2 постоянны и равны, теплоёмкости Ср1 и Ср2 ,
коэффициент теплопередачи h постоянны. Процесс передачи тепла
является стационарным:
Q = ω1 (t1′ − t1′′) = ω2 (t 2′ − t 2′′ ),
(1.3)
ω1 = G1 ⋅ Cò 1; ω2 = G2 ⋅ Cò 2 – водяные эквиваленты,
Q = G1C т1 (t1′ −t ′1 ) = G2C P1 (t 2′ − t 2′′ ) .
Средняя разность температур
∆tср =
∆tб − ∆tм
,
 ∆tб 

ln
 ∆tм 
(1.4)
где ∆tб и ∆tм – больший и меньший температурные напоры между рабочими жидкостями вне зависимости от схемы движения (прямоток
∆t
или противоток). Если á
≤ 1,7 , то
∆tì
∆tб + ∆tм
(1.5)
.
2
Для однотрубного теплообменного аппарата (см. рис.1.1) в случае прямотока ∆tб = t 2′ − t1′; ∆tм = t2′′ − t1′ , в случае противотока
∆tб = t2′ − t1′′; ∆tм = t2′′ − t1′.
Для сложных теплообменных аппаратов, где число труб больше 1, а жидкости текут непараллельно, средний температурный напор
определяют по формуле
∆tср =
′ = ∆tср ⋅ ε ∆t ,
∆tср
где ε∆t – поправочный коэффициент, ε∆t ≤ 1.
Наиболее эффективен теплообменный аппарат из одной трубы с
противотоком, для него ε ∆t = 1 . Критерием для оценки эффективности служит ∆tср. В противоточной схеме ∆tср больше, чем в прямоточной, следовательно, поверхность теплообменного аппарата будет
меньше, т.е. компактнее. Кроме того, при противотоке можно полу5
чить более высокую конечную температуру t1′′ для нагреваемой жидкости, чем при прямотоке, t1′′ может стать даже выше t2′′ греющей
жидкости на выходе, что в прямоточной схеме невозможно.
Вернёмся к задаче определения площади поверхности нагрева
теплообменного аппарата. Из (1.1) и (1.3)
A=
ω1 (t1′ − t1′′)
ω (t ′ − t ′′ )
или A = 2 2 2 ,
∆tср ⋅ h
∆tср ⋅ h
A=
G ⋅ C P1 (t1′ − t1′′)
.
∆tср ⋅ h
(1.6)
(1.7)
Возможности повышения h. Тепловое сопротивление стенки δ
мало в сравнении с 1
α1
è 1
α2
h=
, тогда δ
α1 ⋅ α 2
.
α1 + α 2
λ
λ
можно пренебречь, а
(1.8)
Если α1>>α2 , то h можно повысить, увеличивая только α2, а увеличение в этих условиях α1 не даёт результата. Величины α1 и α2 связаны с гидравлическим сопротивлением движению. Обычно повышение α1 и α2 приводит к повышению гидравлического сопротивления и
затрат мощности на прокачку или повышению падения давления в
теплообменном аппарате.
Более высокие коэффициенты теплоотдачи достигаются при поперечном, а не продольном обтекании труб. Для создания перекрёстного обтекания в межтрубном пространстве внутри кожуха устанавливают перегородки, либо используют перекрестноточные рекуператоры.
Гидравлическое сопротивление элементов рекуператора определяет мощность на прокачивание теплоносителей. Рациональным бывает такой теплообменный аппарат, в котором на единицу переданной
теплоты Q от одного теплоносителя к другому затрачивается минимально возможная мощность N.
Совершенство рекуператора можно охарактеризовать отношением теплового потока Q через данную поверхность теплообменного
аппарата к мощности N, затраченной на прокачку:
6
Q
(1.9)
,
N
N = V ⋅ ∆p , V – объемный расход теплоносителя,
E=
где Q = h ⋅ ∆tср ⋅ A;
м3/с, ∆p – полное гидравлическое сопротивление движению теплоноl ρ ⋅W 2
сителя: ∆ р = ∆ рТр + ∆р м , ∆ рТр = ξ
– сопротивление треd 2
ния, Па; ξ – коэффициент сопротивления трения; l – длина канала, м;
4 ⋅ S0
, S 0 – площадь поп
перечного сечения, м2, П – смоченный периметр, м); ρ – плотность
теплоносителя, кг/м3; W – скорость движения теплоносителя, м/с;
ρ⋅ W 2
– местное сопротивление, Па; ξм – коэффициент
∆ рм = ξ м
2
местного сопротивления.
Для гладких прямых каналов коэффициент ξ можно определить в
зависимости от режима течения.
При ламинарном неизотермическом потоке
d – диаметр канала (для некруглых d = d Эк =
ξ=
А0
Re f
 Prw 


 Pr f 
0,33 
 Gr ⋅ Pr f
1 + 0.22 ⋅  f

 Re f



0,15 
A
≈ 0 ,
 Re f
(1.10)
ν µ CP
(А0 равно 64; 57; 96 для круглого, квадратного и
=
a
λ
кольцевого поперечных сечений канала соответственно).
При турбулентном неизотермическом потоке
где Pr =
ξ=
0.316  Prw 


Re 0f, 25  Pr f 
0,33
,
(1.11)
где Prw определяется при температуре стенки; Grf, Prf, Ref определены
 Pr 
при средней по длине температуре Tf потока;  f  учитывает влия Prw 
ние направления теплового потока.
Как правило, мощность на прокачку теплоносителей определяется из оптимизации всей теплоиспользующей установки и при расчёте
рекуператора используется как предельно допустимая величина.
7
В этом случае для заданных Q и tср эффективность теплообменного
аппарата будет определяться рациональным распределением мощности N между теплоносителями, при котором достигается максимальное значение h.
Определение α:
• турбулентный режим (Re > 1000):
Nu = 0,022 ⋅ Re 0f.8 ⋅ Pr 0f .43 ;
•
(1.12)
ламинарный режим:
Nu = 0.15 ⋅ Re 0.33 ⋅ Pr 0.43 (Nu ≅ 3,7).
(1.13)
Для цилиндра коэффициент теплоотдачи
hц =
1
1 r
1 
 1
+ ln 2 +


 α Ι ⋅ r1 λ r1 α ΙΙ ⋅ r2 
.
(1.14)
1
Тепловой поток Q = hц ⋅ ∆t .
r
При проектировании рекуператора необходимо определить температуры теплоносителей на входе и выходе из теплообменника.
1.1.2. Регенератор
Поверхность регенеративных теплообменников попеременно
омывается то “горячим”, то “холодным” теплоносителем (рис. 1.3).
теплоёмкий наполнитель
газ
ТЗП
Рис. 1.3. Схема регенератора
8
Время, за которое происходит нагревание насадки и охлаждение
“горячего” теплоносителя – τ1, называют периодом нагрева, а время,
за которое происходит охлаждение насадки и нагрев “холодного”
теплоносителя – τ2, – периодом охлаждения. Время полного периода
или цикла:
τпер = τ1 + τ2,
(1.15)
в общем случае τ1 ≠ τ2.
В качестве насадки используются частицы произвольной формы,
выполненные в виде шаров, сетки, решётки и пр., через которые последовательно прокачиваются “холодный” и “горячий” теплоносители. Существуют конструкции с вращающимися теплообменниками.
Поскольку процесс теплообмена в регенераторе является нестационарным, то тепловой расчёт достаточно затруднён. Все расчёты
приходится вести по средним за период характеристикам, тепловой
поток берётся не за единицу времени, а за период.
Уравнение теплового баланса практически не отличается от аналогичного уравнения для рекуператоров:
(
)[
Q = hn t1 − t2 , Äæ (ì 2 ⋅ ïåðèîä)
],
(1.16)
где hn – коэффициент теплопередачи за период нагревания и охла-
[
]
ждения, Ä æ (ì 2 K ⋅ ïåðèîä) ;
t1 – средняя температура “горячего”
теплоносителя за период нагревания; t 2 – средняя температура “холодного” теплоносителя за период охлаждения.
Расчёт коэффициента теплопередачи. Количество тепла, переданное единице поверхности в период нагрева:
(
)
Q1 = α 1τ1 t1 − tc1 ,
(1.17)
где α1 – суммарный коэффициент теплоотдачи за период нагревания;
tc1 – средняя температура поверхности в данном сечении за период
нагревания.
Количество тепла, переданное “холодному” теплоносителю за
период охлаждения:
(
)
Q2 = α 2 τ 2 tc 2 − t2 ,
(1.18)
где α2 – суммарный коэффициент теплоотдачи за период охлаждения;
t c 2 – средняя температура поверхности за период охлаждения.
При установившемся состоянии (цикличности) без внешних потерь теплоты Q1 = Q2.
9
Если обозначить ∆tC = tc1 − tc 2 – разность средних температур поверхности за период нагрева и охлаждения, то
tc1 =
α 1τ1 t1 + α 2 τ 2 t2 + α 2 τ 2 ∆tC
.
α 1τ1 + α 2 τ 2
(1.19)
Приравняв (1.16) и (1.17) и подставив tc1 из (1.19), получим
 tc1 − tc 2 
1 −

t1 − t2 

hn =
.
1
1
+
α 1τ1 α 2 τ 2
(1.20)
Если
принять
разность
температур
поверхностей
tc1 − tc 2 = ∆tC = 0 и продолжительность периодов нагрева и охлаждения равной единице, то
hn =
1
.
1
1
+
α1 α 2
(1.21)
Полученное выражение аналогично уравнению коэффициента
теплопередачи для рекуператора, а формулы для расчёта средних за
период температур и теплопередачи в рекуператорах справедливы и
для регенеративных теплообменников. Если в (1.20) принять ∆tC = 0 ,
а τ1 и τ2 произвольными, то получим выражение для коэффициента
теплопередачи “идеального регенератора”, в котором средняя температура поверхности насадки в период нагрева и охлаждения остаётся
одинаковой:
hид =
1
1
1
+
α 1τ1 α 2 τ 2
.
(1.22)
Из (1.20) следует, что если известны α1 и α2, которые могут быть
вычислены, то расчёт регенератора сводится к определению средних
температур поверхности насадки в период нагревания ( ∆tc1 ) и в период охлаждения (∆tc2). Таким образом, в основу расчёта hn можно
положить выражение (1.22) и о совершенстве регенератора судить по
отличию коэффициента hn от идеального hид:
10
hn = hид
где
U
,
V
 2α τ ∆θ + ∆θ 2 
;
U = f1  1 1 , 1
t1 − t2 
 cδρ
(1.23)
(1.24)
 2α τ 
(1.25)
V = f 2  1 1 , η .
 cδρ

Фактор U/V указывает на ухудшения, которое претерпевает hид
вследствие недостаточных теплопроводности и аккумулирующей
способности насадки регенератора. Этим отношением будет характеризоваться КПД поверхности нагрева.
В (1.24) и (1.25) с – удельная теплоёмкость, δ – толщина насадки,
′
′
ρ – плотность насадки, ∆θ 2 = t2 − t20 – изменение температуры “холодного” теплоносителя на входе, η – коэффициент использования
насадки, ∆θ1= t1 − t10 – изменение температуры “горячего” теплоносителя на входе.
Таким образом, по уравнениям (1.23)–(1.25) можно вычислить
коэффициент теплопередачи для любого регенератора. Дальнейший
расчёт производится по формулам, выведенным для рекуператора.
2. УСТРОЙСТВА ДЛЯ ОТВОДА ТЕПЛА В КОСМОСЕ
Энергетическая установка КА, преобразующая тепловую энергию в электрическую, нуждается в отводе тепла в окружающее пространство в соответствии с законами термодинамики. Если КПД
энергетической установки
ηЭУ = 1 −
N отв
,
N отв + N ЭУ
(2.1)
где Nотв – отводимый тепловой поток, Вт; NЭУ – полезная мощность
1 − ηЭУ
ЭУ, Вт, то N отв =
⋅ N ЭУ .
ηЭУ
Поскольку ηЭУ не превышает 30%, то Nотв более чем в два раза
превышает полезную мощность ЭУ.
Отвод тепла с борта КА в космосе без затрат массы какого-либо
рабочего тела может осуществляться только тепловым излучением с
поверхности тел, поэтому устройство отвода тепла в космосе называ11
ют холодильником-излучателем (ХИ), несмотря на то что его температура может составлять сотни градусов. Плоская поверхность площадью S, имеющая минимальную температуру энергетического цикла
в вакууме, лишенном каких-либо тел и источников тепла, излучает,
согласно закону Стефана–Больцмана, тепловую мощность
4
S,
qи = εσ0Tmin
где ε – степень
черноты
поверхности
излучающего
σ0 = 5,67⋅10-8 [Вт/м2⋅К4] – постоянная Стефана–Больцмана.
Если считать, что qи = NОТВ, то
S=
1 − ηЭУ
N ЭУ
.
⋅
4
ε ⋅ σ 0 ⋅Tmin ηЭУ
(2.2)
тела;
(2.3)
ηЭУ связан с Тmax и Тmin ЭУ соотношением
ηЭУ = η*
Tmin
,
Tmax
цикла. Тогда
где T =
η*
Tmax − Tmin
= η* ⋅ (1 − T ),
Tmax
(2.4)
учитывает отличия от идеального энергетического
S=
N ЭУ ⋅ (1 − η∗ ⋅ (1 − T ))
.
4
ε ⋅ σ ⋅Tmax
⋅T 4 ⋅ η∗ ⋅ (1 − T )
(2.5)
При заданных NЭУ, Тmax, ε, σ0 величина S достигает минимума в
соответствии с условием ∂S / ∂T при следующем оптимальном значении:
T opt =−
1
5
5 2 1
+ (1 −
− 1.
) +
η∗
8η∗
8η∗
(2.6)
Т min
3 , т.е. для ми=
Tmax
4
нимизации площади ХИ Tmin должна составлять 75% от Tmax, что
явно противоречит условию максимума КПД термодинамического
цикла.
При полетах в пределах cолнечной системы нужно дополнительно учитывать влияние лучистого теплообмена между рассматриваемой излучающей поверхностью и небесными телами: солнцем и пла-
Если η∗ 1, =
то
Т opt 3
=
4
или
12
нетами. В результате этого рассматриваемая поверхность поглощает
суммарную тепловую мощность, которая зависит от расположения
этой поверхности по отношению к небесным телам, от поглощательной способности поверхности AS и от теплового потока от источника
излучения qC.
Для Солнца в околоземном пространстве qC = 1396 Вт/м2. Отражение от Земли и Луны при средних потоках на солнечной стороне –
350 и 325 Вт/м2 соответственно. Она зависит также от конструкции
ХИ (переизлучения между отдельными частями КА).
Тогда тепловая мощность, излучаемая единичной поверхностью
ХИ, будет равна:
qХИ = εσ0Tn4 − qS .
(2.7)
Для единичной плоской поверхности qS = qC AS cos(γ), где γ – угол
между поверхностью и нормалью падающего теплового потока
(рис. 2.1).
φ
qC
Рис. 2.1. Схема освещения поверхности
На практике желательно уменьшать qS. Для этого существует несколько способов:
1) нанесение на излучающую поверхность ХИ специальных селективных покрытий, обладающих низкой поглощательной способностью AS ≈ 0,15÷0,2 и большой степенью черноты ε ≈ 0,95÷0,98;
2) тепловая изоляция охлаждаемых отсеков (для ХИ энергетической установки невозможна);
3) ориентация излучающей поверхности параллельно направлению падающего потока.
При температурах излучателя в несколько сотен градусов влияние солнечного облучения уже невелико и ориентация на Солнце ска13
зывается слабо. Так, при t = 600°C и ε = 0,9 учет солнечного облучения приводит к поправке ∼3%. Однако в общем случае внешнее облучение должно учитываться.
2.1. Конструктивные средства теплоотвода в космосе
В ЭУ теплоотвод осуществляется не непосредственно, а с помощью теплоносителей или тепловых труб. Теплоноситель направляется
в выносной ХИ. Форма последнего уже не связана с конструкцией ЭУ
и расположением на ней излучаемых поверхностей и может полностью подчиняться условиям оптимального излучения тепла.
Простейшая схема ХИ – труба (рис. 2.2), которая при заданной
температуре теплоносителя и внешних условиях излучает максимально возможную удельную тепловую мощность. Поверхность излучения минимальна, однако масса такого излучателя велика.
qS
Твых
излучение
Твх
теплоноситель
Рис. 2.2. Простейшая схема ХИ – труба
Существенно снизить массу можно введя оребрение (рис. 2.3).
При оптимальном оребрении поверхность увеличивается на 20…30%,
а масса меньше примерно в 2…2.5 раза. При этом уменьшается метеорная опасность.
14
Твых
излучение
Твх
теплоноситель
Рис. 2.3. Холодильник-излучатель с оребрением
2.1.1. Расчёт излучающих рёбер
Допущения:
• ребро достаточно тонкое, поэтому изменением температуры
по толщине пренебрегаем;
∂T
пренебрежимо мал
• градиент температуры по длине ребра
∂z
∂T
;
∂x
• степень черноты и все физические свойства материала ребра
считаем постоянными и не зависящими от температуры.
Рассмотрим участок ребра единичной длины dL = 1, ограниченный абсциссами x и x + dx (рис. 2.4).
За счёт теплопроводности в выделенный участок поступает тепловой поток
dT
(2.8)
Qx = − λ ⋅ δ ⋅
dx x
по сравнению с градиентом
и отводится тепловой поток
15
Qx+dx = −λ⋅ δ ⋅
dT
dx
.
(2.9)
x + dx
T
TОР
x
dx
x
2l
Рис. 2.4. Участок ребра единичной длины
Разность этих величин составляет тепловой поток
d  dT 
(2.10)
dQT =  λδ
dx.
dx  dx 
Наружная поверхность рассматриваемого участка излучает тепловой поток
(2.11)
dQи = mεσ0T 4 dx
(m = 1 – излучает одна сторона, m = 2 – излучают обе стороны).
Кроме того, к выделенному участку за счёт внутренних источников тепла, а также вследствие облучения от посторонних источников,
например Солнца, подводится тепло, которое можно представить в
виде
(2.12)
dQC = qS dx.
При установившемся тепловом состоянии
dQT = dQи − dQ„
(2.13)
Таким образом, получаем уравнение энергии:
d  dT 
4
 λδ
 − mεσ0T + qS = 0,
dx  dx 
которое дополняют граничные условия:
16
(2.14)
dT
(2.15)
= 0.
dx
Можно получить распределение температуры по длине ребра, если решить краевую задачу (2.14) с граничными условиями (2.15).
Для приближенного определения теплового потока, отводимого
от излучающего ребра, на практике используют коэффициент η,
называемый эффективностью ребра, который представляет собой
отношение отводимого ребром от основания потока тепла Qор к тепловому потоку, отводимому ребром при постоянной его температуре,
т.е. при бесконечно большой теплопроводности. Так, для ребра постоянного сечения
при x = 0: T = Тор, при x = l: − λδ
η=
Qop
mεσ0Top4 l
.
(2.16)
2.1.2. Расчет длины ХИ
Для того чтобы определить площадь поверхности ХИ, кроме
длины рёбер должна быть определена длина ХИ (рис. 2.5), которую
можно найти, если рассмотреть тепловой баланс трубки с теплоносителем.
Т
Твх
Твых
z
т/н
Рис. 2.5. Изменение температуры по длине ребра и трубок ХИ
17
Тепловая мощность теплоносителя на элементарной длине секции dL:
dQтепл = – с⋅G⋅dTтепл,
(2.17)
где Tтепл – текущая температура теплоносителя; с – теплоёмкость теплоносителя; G – расход теплоносителя, кг/с2.
Тепловой поток от теплоносителя в стенку трубки определяется
температурным напором Tтепл − Т ор :
dQст = α(Tтепл − Т ор )πDк dL,
(2.18)
где α – коэффициент теплоотдачи; Dк – внутренний диаметр канала.
Тепловой поток, излучаемый ребром на участке dL:
dQи = 2Qор dL.
(2.19)
Коэффициент 2 учитывает, что на одну трубку приходится два ребра.
Qор можно определить, решив уравнение (2.14) с граничными
условиями (2.15).
При установившемся тепловом режиме
dQтепл = dQст = dQи .
(2.20)
Уравнения (2.19) и (2.18) при заданной геометрии ребер и трубки
дают взаимосвязь между Tтепл и Тор. Это взаимосвязь сложная, поскольку коэффициент α зависит от параметров потока и геометрии
трубки, Qор изменяется вдоль трубки.
Из (2.17) и (2.18) можно получить уравнение
α
dTтепл
(T − Т )πDк ,
=−
dL
CG тепл ” р
(2.21)
начальные условия L = 0, T = Tвх. Тор определяется из соотношения
(2.20): dQтепл = dQст,
α(Tтепл − Т ор )πDк = 2Qор .
(2.22)
Qор находится из решения краевой задачи распределения температуры по длине ребра (2.14).
Совместное решение (2.14), (2.21), (2.22) позволяет определить
распределение температуры как по длине ребра, так и по длине трубки ХИ.
Для приближённого расчёта потребной поверхности ХИ для случая qS = 0 можно рекомендовать выражение
18
S=
(
3
3
QИ ⋅ 1 Tвых
− 1 Tвх
),
3mεσ0 η (Т вх − Т вых )
(2.23)
где QИ – излучаемая мощность, Вт; Твх – температура на входе в ХИ;
Твых – температура на выходе из ХИ; η – эффективность ребра.
2.2. Перспективные устройства отвода тепла в космосе.
Расчёт ленточного излучателя
Существенным недостатком стационарных ХИ с большой площадью поверхности является опасность повреждения метеорами.
В связи с этим перспективным считается нестационарный излучатель.
В этих излучателях тепло от исходного жидкого или газообразного
теплоносителя воспринимается за счёт теплоёмкости некоторым телом
(лентой, диском, шариками) в определённом малогабаритном устройстве. Затем нагретое тело удаляют на некоторое расстояние в космос,
где оно, излучая тепло, охлаждается, и цикл повторяется вновь. Опасность метеорного повреждения такого ХИ будет значительно меньше.
Однако полная поверхность всех излучающих тел будет больше, чем
для стационарного ХИ, за счёт того, что средняя температура поверхности будет меньше. Кроме того, требуется существенная мощность для
приведения данного ХИ в "движение". На рис. 2.6 представлен дисковый излучатель, а на рис. 2.7 – ленточный излучатель с барабаном.
Рис. 2.6. Дисковый излучатель, 1 – вращающийся диск, 2 – теплоноситель,
3 – неподвижный корпус
19
Лента имеет два участка (рис. 2.7): один, длиной L, излучает тепловую энергию в космос; другой, длиной l, получает тепло от теплового источника, нагреваясь от температуры Т1 до Т0.
Рис. 2.7. Ленточный излучатель
При расчёте используются следующие допущения:
• лента довольно тонкая и можно пренебречь изменением температуры по толщине и растеканием тепла вследствие теплопроводности;
• физические свойства материала ленты постоянны и не зависят от Т.
Участок отвода тепла. Уравнение энергии для движущейся ленты будет одномерным. Движущуюся ленту можно рассмотреть как стационарный поток вещества с постоянной скоростью V
и "массовым расходом" Gл, тогда уравнение энергии будет иметь
вид
20
c л Gл
dT
= −(ε′ + ε′′ )σ 0 dzT 4 + qS dz ,
dx
(2.24)
где сл – теплоёмкость материала ленты, Gл = ρ л δ лV dz – "массовый"
расход ленты; ρл – плотность; δл – толщина ленты; ε′, ε′′ – степени
черноты наружной и внутренней поверхностей ленты; qS – тепло, поглощаемое единицей поверхности ленты от каких-либо источников.
Рассмотрим случай, когда qS = 0, обозначив
Т=
(ε′ + ε′′)σ0 LT03dz .
Т
x
; x = ; Nо =
Т0
L
c л ⋅ Gл
(2.25)
Подставив (2.25) в (2.24), получим
4
dT
+ N л ⋅Т = 0
dx
(2.26)
при начальном условии T = 1 при x = 0.
T
∫
1
dT
T
4
x
= ∫ − N л d x , решение которого
0
(
Т = 1 + 3N л x
)
−1
3
.
(2.27)
Относительная температура в конце участка а (при x = 1 ):
Т 1 = (1 + 3 N л )
−1
3.
(2.28)
Определение ширины ленты. Теплоноситель течёт по трубе с
расходом GTH, при этом на длине трубы, равной ширине ленты, он
изменяет температуру от Tвх до Твых. Задача состоит в определении
ширины ленты b.
Тепловая мощность, рассеиваемая лентой шириной dZ:
dQл = cл ⋅ Gл ⋅ (Т 0 Z − T1Z ) ,
(2.29)
где Т 0 Z – температура ленты на выходе с нагревательного барабана в
точке с координатой Z, T1Z – на входе барабана после охлаждения.
Тепловая мощность, теряемая теплоносителем на участке dZ:
dQтепл = −cТН GTH ⋅ dTтепл ,
(2.30)
где сТН – теплоёмкость теплоносителя; GТН – "массовый расход" теплоносителя, кг/с.
21
Допущения:
1. Тепло с ленты излучается только наружной поверхностью,
распространением тепла в направлении перпендикулярном скорости
пренебрегаем, т.е. уравнение теплопроводности одномерное.
2. Пренебрегаем самооблучением ленты.
3. Температура ленты T0 Z в точке схода с нагревательного
барабана равна
Т 0 Z = Tтепл = Т .
Тогда
температуре
теплоносителя
в
данной
dQтепл = dQо .
точке:
(2.31)
Температура ленты в точке L из (2.28): Т1Z = T0 Z (1 + 3 N л )
Подставив dQл и dQтепл в (2.31), получим
−1
3.
1


3 −3 
 

εσ0 LT

cлρ л δVdz ⋅T 1 − 1 + 3
= −cТН ⋅ GТН ⋅ dTтепл . (2.32)
cлρ л δV  
 


Проинтегрировав по Z от 0 до b и по Ттепл от Твх до Твых, окончательно получим
c ⋅ G Т вх
dT
.
(2.33)
b = ТН ТН ∫
1
cлρ л δV Т вых
εσ0 LT 3 − 3
T (1 − (1 + 3
) )
cлρ л δV
Для определения параметров ленточного излучателя необходимо
задать L, δ, V.
Для уменьшения массы ленты выгодно увеличивать скорость.
Однако увеличение скорости ограничено допустимыми напряжениями на разрыв ленты вследствие больших центробежных усилий
(Vдоп = 10…30 м/c).
Для ПТУ температура теплоносителя в ХИ постоянна и равна
температуре насыщения, тогда ширина ленты b определится из
условий:
• тепловая мощность, рассеиваемая лентой шириной b:
dQл = cлGл (Т 0 − Т1 );
(2.34)
• тепловая мощность, теряемая теплоносителем на участке b1,
равна теплоте парообразования r при данном давлении:
(2.35)
dQл = r.
22
Тогда из условия dQл = dQтепл
1

− 
 
εσ0 LT03  3 
  = r,
cлρ лVδbТ 0 1 − 1 + 3

V
c
ρ
δ
л
л
л
 
 


b=
r
1

− 
 
εσ0 LT03  3 
 
cлρ лVδТ 0 1 − 1 + 3

ρ
δ
c
V
л
л
л
 
 


.
(2.36)
(2.37)
2.3. Метеорная опасность в космосе
При расчёте и проектировании ХИ одним из наиболее важных
моментов, определяющих вес излучателя, является выбор потребной
толщины каналов, по которым течёт теплоноситель, толщина определяется прочностью и противометеорной защитой.
Метеоры – тела внеземного происхождения. Попадая в атмосферу, они сгорают, а если не успевают сгореть и достигают земли, то их
называют метеоритами.
Метеоры делятся на два класса: входящие в метеорные потоки и
не входящие, или спорадические. Метеорных потоков следует избегать, а все рассуждения относятся к спорадическим метеорам. Их
средняя скорость 30…40 км/с. Максимум спорадических метеоров
достигается в 6 часов местного времени и в осенние месяцы. Плоскость их основного движения близка к плоскости эклиптики, 50% метеоров находятся в угле ±15° от этой плоскости.
При взаимодействии метеора с поверхностью ХИ возможны либо
эрозия, либо пробой поверхности. Эрозию создают метеоры с массой
менее 10–4…10–3г, причём наибольшую часть материала распыляют
метеоры массой 10–7г. При массе более 10–4…10–3г возможен пробой
сравнительно тонких металлических поверхностей.
Толщина неповреждаемой пластины, по американским данным,
δ=
1410
( )
1
ρв 6
 F ⋅τ 
1  − ln P 
0 
3 
1
4
мм,
(2.38)
⋅ Eв
где ρв – плотность материала пластины, Г/СМ3; Ев – модуль упругости
вещества при соответствующей температуре, Н/м2; Р0 – коэффициент
23
надёжности или вероятность отсутствия пробоя за время τ; τ – время
работы, сут; F – площадь, м2. Так, для стали при T = 500°С,
ρв = 7,8 г/см3, Ев = 1.7⋅1011 Н/м2.
Влияние материала на толщину стенки. Лучшими материалами
по минимуму веса являются бериллий, пиролитический графит и
алюминий. Стальной излучатель в шесть раз, а медный в четыре раза
тяжелее бериллиевого. Однако при анализе следует учитывать и испаряемость металла. Для повышения надёжности ХИ в отношении
метеорного пробоя может быть использован ряд мероприятий:
• уменьшение метеороопасной поверхности. Может быть использован при высокой температуре в излучателе и снижении количества отводимого тепла;
• введение защитных экранов. При столкновении метеора со
сравнительно тонкой преградой и пробивании её за счёт испарения
метеора и преграды (части её) резко снижается кинетическая энергия
продуктов;
• секционирование излучателя.
Библиографический список
1. Ходосов В.В. Энергетические установки КА / Балт. гос. техн. ун-т. СПб.,
2017.
2. Козлов А.Г., Ходосов В.В. Системы электропитания космических аппаратов / Балт. гос. техн. ун-т. СПб., 2011.
3. Гущин В.Н. Основы устройства космических аппаратов. М.: Машиностроение, 2003.
4. Квасников Л.Н. и др. Теория и расчет энергосиловых установок космических летательных аппаратов. М.: Машиностроение, 1984.
5. Керн Д., Краус А. Развитые поверхности теплообмена. М.: Энергия, 1977.
24
ОГЛАВЛЕНИЕ
1. ОБЩИЕ СВЕДЕНИЯ О ТЕПЛООБМЕННЫХ УСТРОЙСТВАХ ЭНЕРГЕТИЧЕСКИХ УСТАНОВОК .................................................................................... 3
1.1. Теплообменные аппараты ................................................................................ 3
1.1.1. Рекуператор.............................................................................................. 3
1.1.2. Регенератор .............................................................................................. 8
2. УСТРОЙСТВА ДЛЯ ОТВОДА ТЕПЛА В КОСМОСЕ ........................................11
2.1. Конструктивные средства теплоотвода в космосе........................................14
2.1.1. Расчёт излучающих рёбер ......................................................................15
2.1.2. Расчет длины ХИ.....................................................................................17
2.2. Перспективные устройства отвода тепла в космосе. Расчёт ленточного излучателя .....................................................................................................19
2.3. Метеорная опасность в космосе .....................................................................23
Библиографический список .........................................................................................24
Ходосов Владимир Викторович
Теплообменные устройства энергетических установок
космических аппаратов
Редактор Г.М. Звягина
Корректор Л.А. Петрова
Компьютерная верстка: С.В. Кашуба
Подписано в печать 10.09.2018. Формат 60х84/16. Бумага документная.
Печать трафаретная. Усл. печ. л. 1,45. Тираж 100 экз. Заказ № 129.
Балтийский государственный технический университет
Типография БГТУ
190005, С.-Петербург, 1-я Красноармейская ул., д.1