ТиПИИ, Канев КР.

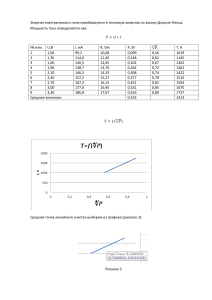
Федеральное государственное бюджетное образовательное учреждение
высшего образования
"Калининградский государственный технический университет"
(ФГБОУ ВПО «КГТУ»)
Кафедра судовых энергетических установок и теплоэнергетики
Контрольные работы
по дисциплине: «Теория и практика инженерного исследования»
Работу выполнил:
студент группы 21-ЗТЭ
Канев А.А.
Вариант 8
Работу проверил:
проф. Герасимов А.А.
Калининград
2022 г.
Работа №1
Вычисление статистических показателей малой выборки
Задание:
В результате исследования было получено 30 измерений перепадов температуры на
внутренней и наружной поверхностях изоляции теплопровода. Значения приведены в
таблице 1.
Необходимо рассчитать основные статистические показатели. Установить достоверность
и различие вычисленных средних значений. Сделать выводы.
Таблица 1
t, oC
1,8
2
1,0
1,1
1,4
1,9
2
1,6
1,5
1,2
1,6
1,2
1,5
1,5
1,7
1,9
1,6
2,0
2,1
1,3
1,1
1,2
1,4
1,4
1,4
1,5
1,2
1,4
1,6
1,5
Решение:
В практике статистического анализа принято рассчитывать шесть основных
характеристик вариационного ряда:
1. Среднее значение М - это обобщающая характеристика изучаемого признака в
исследуемой совокупности, отражающая его типичный уровень в расчёте на единицу
совокупности в конкретных условиях.
(1)
М=
1,8+1,1+2+1,2+1,5+1,9+2,1+1,2+1,4+1,4+2+1,4+1,6+1,6+1,5
30
1,6+1,3+1,4+1,5+1,6+1,0+1,9+1,5+1,2+1,7+2,0+1,1+1,4+1,2+1,5
30
где x1, х2, …, хn – варианты совокупности;
n – количество единиц наблюдения.
+
= 1,52
2. Среднее квадратичное отклонение (или стандартное отклонение σ) – это основной
показатель изменчивости (вариации) ряда распределения или среднее отклонение
отдельных вариант выборки от среднего значения, измеряющееся в тех же единицах.
(2)
(1,8 − 1,52)2 + (1,1 − 1,52)2 + (2 − 1,52)2 + (1,2 − 1,52)2 + (1,5 − 1,52)2 + (1,9 − 1,52)2 + (2,1 − 1,52)2 + (1,2 − 1,52)2
+
29
(1,4 − 1,52)2 + (1,4 − 1,52)2 + (2 − 1,52)2 + (1,4 − 1,52)2 + (1,6 − 1,52)2 + (1,6 − 1,52)2 + (1,5 − 1,52)2 + (1,6 − 1,52)2
+
29
𝜎=
(1,3 − 1,52)2 + (1,4 − 1,52)2 + (1,5 − 1,52)2 + (1,6 − 1,52)2 + (1,0 − 1,52)2 + (1,9 − 1,52)2 + (1,5 − 1,52)2 + (1,2 − 1,52)2
+
29
2
2
2
2
2
2
(1,7 − 1,52) + (2,0 − 1,52) + (1,1 − 1,52) + (1,4 − 1,52) + (1,2 − 1,52) + (1,5 − 1,52)
= 0,299
29
√
3. Основная ошибка среднего значения mM - выражает величину, на которую
отличается среднее значение выборки от среднего значения генеральной совокупности.
Основная ошибка, как правило, записывается вместе со средним значением через знак ±, и
измеряется в тех же единицах.
2
(3)
𝑚𝑀 =
0,299
√30
= 0,0545
4. Коэффициент изменчивости (или вариации С) – основное отклонение, выраженное в
процентах от среднего значения. Изменчивость считается малой, если С <10,0%; средней
– С=10,1…30,0% и большой, при С>30,1%.
(4)
0,299
С=
∗ 100 = 19,67%
1,52
5. Точность опыта p – служит оценкой ошибки наблюдения и характеризует
расхождения между выборочной и генеральной средними. Точность опыта считается
высокой, если P<5% или удовлетворительной (при P от 6 до 10%). В других случаях
результаты считаются не точными.
(5)
0,0545
Р=
∗ 100 = 3,58%
1,52
6. Достоверность среднего значения tМ – это показатель надёжности среднего значения,
численно равный отношению среднего значения к его основной ошибке. Среднее
значение достоверно, если tM > 4. Результаты исследований считаются достоверными,
если tM ≥ 3. В том случае, если показатель достоверности менее трёх, среднее значение
нельзя использовать при формулировании выводов.
𝑡𝑀 =
1,52
= 27,8
0,0545
Вывод:
Полученные в результате исследования значения температуры соответствуют: среднему
коэффициенту изменчивости (С=10,1…30,0%); высокой точности опыта (P<5%);
достоверности среднего значения (tM > 4), следовательно, исходные данные можно
считать верными.
3
Работа №2
Достоверность различия средних значений
Задание:
В результате работы двух групп исследователей А и Б было получено 8 и 10
измерений скоростей движения теплоносителя в теплопроводе.
Необходимо рассчитать tразл предварительно вычислив для каждой из групп
статистические показатели. Найти для различных вероятностей безошибочного
заключения tst и сравнить с tразл. Сделать выводы.
Таблица 1
№ измерения
Скорость
теплоносителя,
м/с
А
1
1,81
2
1,13
3
2,04
4
1,25
5
1,59
6
1,90
7
2, 16
8
1,2
9
-
10
-
Б
2,01
1,48
1,64
1,67
1,57
1,67
0,57
1,44 1,58 1,66
Решение:
Анализ достоверности различия средних значений (tразл.) имеет практическое
значение при оценке статистической значимости разности выборочных средних величин в
сопоставляемых распределениях. Для расчёта tразл. (формула (7)) требуется найти
основные статистические показатели выборок.
,
(7)
где M1 и M2 – средние значения в сравниваемых выборках по (1), m1 и m2 – ошибки
средних значений по (3).
1,81 + 1,13 + 2,04 + 1,25 + 1,59 + 1,90 + 2,16 + 1,2
= 1,635
8
2,01 + 1,48 + 1,64 + 1,67 + 1,57 + 1,67 + 0,57 + 1,44 + 1,58 + 1,66
М2 =
= 1,529
10
М1 =
(1,81 − 1,635)2 + (1,13 − 1,635)2 + (2,04 − 1,635)2 + (1,25 − 1,635)2 + (1,59 − 1,635)2 + (1,90 − 1,635)2
+
7
𝜎1 = √
2
2
(2,16 − 1,635) + (1,2 − 1,635)
= 0,402
7
(2,01 − 1,529)2 + (1,48 − 1,529)2 + (1,64 − 1,529)2 + (1,67 − 1,529)2 + (1,57 − 1,529)2 + (1,67 − 1,529)2
+
9
𝜎2 = √
(0,57 − 1,529)2 + (1,44 − 1,529)2 + (1,58 − 1,529)2 + (1,66 − 1,529)2
= 0,407
9
𝑚𝑀1 =
𝑚𝑀2 =
𝑡разл. =
0,402
√8
0,407
= 0,142
= 0,128
√10
1,635 − 1,529
= 0,828
√0,1422 + 0,1282
Критическое значение критерия tst для двух вариационных рядов определяется по
таблице 2 с учётом уровня значимости и числа степеней свободы (n1). Общее число
степеней свободы рассчитывается по формуле (8):
4
(8)
где n1 и n2 – количества переменных в выборках.
𝑛 = 8 + 10 − 2 = 16
При t разл.≥tst различие в средних на выбранном уровне значимости считается
доказанным, в противном случае различия нет.
Стандартные значения критерия Стьюдента
Таблица 2
Число
степеней
свободы
Уровень значимости
при вероятности
безошибочного
заключения р
0,5 0,9
16
0,95 0,99 0,999
0,69 1,75 2.12 2,92 4,02
При р = 0,5
t разл.≥tst, 0,828 ≈ 0,69
При р = 0,9; 0,95; 0,99; 0,999
t разл.< tst
Вывод:
Так как при вероятности безошибочного заключения р = 0,5 t разл.≥tst, то различие в
средних на выбранном уровне значимости доказано. При р = 0,9; 0,95; 0,99; 0,999
различий нет.
Работа №3
Установление уровня связи между исследуемыми показателями
Задание:
Требуется установить характер корреляционной связи между расходом теплоносителя
(кг/час) в отопительном приборе и тепловым потоком этого прибора (Вт/м2). Значения
приведены в таблице 1. Выполнить расчет для всех указанных выше характеристик
корреляции. Расчет вести в таблице 3. Значение tфакт сравнить с коэффициентом
Стьюдента при различных уровнях значимости. По результатам сделать вывод.
Решение:
Таблица 1
№
Расход,
кг/час, (х)
Тепловой
поток,
Вт/м2, (у)
1
2
3
4
5
6
7
8
9
309
310
322
336
356
383
388
372
345
427
428,3
430,7
432,7
437,3
441,5
442,9
440,2
435,2
5
Тесноту корреляции, или степень сопряжённости между значениями одного и другого
признака, выражают в виде отвлеченной статистической характеристики (показателя)
связи – коэффициента корреляции r. Он изменяется в пределах от 0 до +1 (при прямой
зависимости) и от 0 до -1 (при обратной связи). Если по расчётам r =1, то такую связь
называется функциональной.
Оценки коэффициента корреляции
Таблица 2
Коэффициент корреляции, r
Оценка тесноты связи
менее 0.30
0,31...0,50
0,51...0.70
0,71...0.90
0.91 и более
слабая
умеренная
значительная
высокая
очень высокая
Расчёт коэффициента корреляции (r) по Пирсону проводится по формуле (9):
(9)
Результаты вычислений:
Таблица 3
Признаки
№
Xi
Yi
1
2
3
4
5
6
7
8
9
309
310
322
336
356
383
388
372
345
427
428,3
430,7
432,7
437,3
441,5
442,9
440,2
435,2
Хi - Мx Уi- Му
37,77
36,77
24,77
10,77
9,23
36,23
41,23
25,23
1,77
8,08
6,78
4,38
2,38
2,22
6,42
7,82
5,12
0,12
(Хi - Мх)*
(Yi-My)
305,181
249,3
108,492
25,632
20,49
232,596
322,418
129,177
0,212
(Xi-Mx)2
(Yi-My)2
1426,572
1352,032
613,552
115,992
85,192
1312,612
1699,912
636,552
3,132
65,286
45,968
19,184
5,664
4,928
41,216
61,152
26,214
0,014
309 + 310 + 322 + 336 + 356 + 383 + 388 + 372 + 345
= 346,77
9
427 + 428,3 + 430,7 + 432,7 + 437,3 + 441,5 + 442,9 + 440,2 + 435,2
М𝑦 =
= 435,08
9
М𝑥 =
𝑟
=
305,181 + 249,3 + 108,492 + 25,632 + 20,49 + 232,596 + 322,418 + 129,177 + 0,212
√(1426,57 + 1352,03 + 613,55 + 115,99 + 85,19 + 1312,61 + 1699,91 + 636,55 + 3,12) ∗ (65,2 + 45,9 + 19,1 + 5,6 + 4,9 + 41
= 0,996
Ошибка коэффициента корреляции (mr) рассчитывается по формуле (10):
6
(10)
𝑚𝑟 =
1 − 0,9962
= 0,002661
√9
Достоверность коэффициента корреляции (tr) определяется по формуле (11):
(11)
0,996
𝑡𝑟 =
= 374,295
0,002661
Проверка значимости коэффициента корреляции (tфакт.) проводится по формуле (12):
(12)
где n – число наблюдений (объём выборки);
𝑡факт. =
0,996√9 − 2
√1 − 0,9962
= 29,60
Полученное значение сравнивается с табличным значением критерия Стьюдента tst,
определённым на уровне значимости α с числом степеней свободы (n – 2) и если
неравенство tфакт.≥tst выполняется, то связь доказана на заданном уровне значимости.
Число
степеней
свободы
Таблица 4
Уровень значимости
при вероятности
безошибочного
заключения р
0,5 0,9
7
0,95 0,99 0,999
0,71 1,89 2,36 3,50 5,41
Коэффициент (или индекс) детерминации - показывает долю изменений зависимой
переменной y с изменением независимой переменной x. Для его получения нужно
возвести в квадрат коэффициент корреляции η = (r)2.
Вывод:
Согласно расчету коэффициент корреляции r = 0,996 ≈ 1, следовательно, связь можно
назвать очень высокой или же функциональной. Что подтверждается выполнением
неравенства tфакт.≥tst , связь доказана на заданном уровне значимости.
7
Работа №4
Определение основных статистических характеристик средствами Excel
Задание:
1. Внесите данные для своего варианта в таблицу Excel в соответствии с примером
2. Определите в ячейке В9 среднее значение расхода для здания В.
3. Определите в ячейке В10 стандартное отклонение расхода для здания В.
4. Найдите медиану, моду, дисперсию и стандартное отклонение.
5. Определите выборочные асимметрию и эксцесс.
6. Постройте гистограмму
Решение:
Таблица 1
Вариант Здание
1
А
В
Расходы газа, м3/ч
222, 209, 217, 189, 192, 185, 189, 219, 194
180, 175, 162, 168, 171, 179, 160, 165, 177
1. Вводим в ячейку А1 текст Здание А, затем в ячейки А2:А8 — соответствующие
значения расхода для А. В ячейку В1 введите текст Здание В, а в В2:В8 — значения для
здания Б. Эти группы данных со статистической точки зрения являются выборками.
2. Для определения среднего значения в контрольной группе необходимо установить
табличный курсор в свободную ячейку (А9). На панели инструментов жмем кнопку
Вставка функции (fx). В появившемся диалоговом окне Мастер функций выберите
категорию Статистические и функцию СРЗНАЧ, после чего нажмите кнопку ОК.
Указателем мыши введите диапазон данных контрольной группы для определения
среднего значения (А2:А8). Нажмите кнопку ОК. В ячейке А9 появится среднее значение
выборки.
3. Для определения стандартного отклонения в здании А необходимо установить
табличный курсор в свободную ячейку (А10). На панели инструментов нажимаем кнопку
Вставка функции (fx). В появившемся диалоговом окне Мастер функций выбираем
категорию Статистические и функцию СТАНДОТКЛОН, после чего жмем кнопку ОК.
Указателем мыши вводим диапазон данных контрольной группы для определения
стандартного отклонения (А2:А8). Нажимаем кнопку ОК. В ячейке А10 появится
стандартное отклонение выборки.
4. Функция МЕДИАНА позволяет получать медиану заданной выборки. Медиана — это
элемент выборки, число элементов выборки со значениями больше которого и меньше
которого равно. Например, МЕДИАНА(4;14;5;6;10;12;13) равняется 10.
5. Функция МОДА вычисляет наиболее часто встречающееся значение в выборке.
Например, МЦА(10;14;5;6;10;12;13) равняется 10.
6. Функция ДИСП позволяет оценить дисперсию по выборочным данным. Например,
ДИСП (10;14;5;6;10;12;13) равняется 11,667.
7. Функция ЭКСЦЕСС позволяет оценить степень выраженности «хвостов»
распределения, то есть частоты появления удаленных от среднего значений.
8. Функция СКОС позволяет охарактеризовать несимметричность распределения элементов выборки относительно среднего значения. Принимает значения от -1 до 1. В
случае симметричного распределения асимметрия равна 0.
8
10. Полученные значения:
Среднее значение
Стандартное отклонение
Медиана выборки
Наиболее встречающиеся
значения
Дисперсия
Степень выраженности
хвостов
Несимметричность
распределения
А
201,7778
14,80522
194
Б
170,7778
7,446103
171
189
-
219,1944
55,44444
-2,02381
-1,58932
0,345729
-0,18927
11. Создадим гистограмму в приложении Excel:
Вывод:
Испытали специальные функции Excel, применив их к выборкам суточного расхода газа
двух зданий. Удалось реализовать все функции из контрольной работы.
Работа №5
Построение линейной зависимости регрессии
Задание:
Построить линейную зависимость регрессии по экспериментальным точкам, значения
которых приведены в предыдущем задании (работа №3, табл. 1). Получить уравнение
регрессии, построить в одной системе координат эмпирическую и теоретическую линии.
Решение:
Расположим исходные данные в порядке возрастания:
9
Таблица 1
№
Расход,
кг/час, (х)
Тепловой
поток,
Вт/м2, (у)
1
2
3
4
5
6
7
8
9
309
310
322
336
345
356
372
383
388
427
428,3
430,7
432,7
435,2
437,3
440,2
441,5
442,9
Получим график:
Для линейной зависимости линия регрессии задается уравнением прямой,
,
(13)
неизвестные коэффициенты определяются по методу наименьших квадратов. В
соответствии с этим методом, квадрат расстояния по вертикали между опытными точками
с координатами xi,yi и соответствующими точками на линии регрессии должно быть
минимальным.
Уравнение регрессии принимает вид:
(14)
где
(15)
(16)
10
Результаты вычислений:
Таблица 2
Признаки
№
Xi
Yi
1
2
3
4
5
6
7
8
9
М𝑥 =
М𝑦 =
𝛽=
309
310
322
336
356
383
388
372
345
Хi - Мx Уi- Му
427
428,3
430,7
432,7
437,3
441,5
442,9
440,2
435,2
37,77
36,77
24,77
10,77
9,23
36,23
41,23
25,23
1,77
8,08
6,78
4,38
2,38
2,22
6,42
7,82
5,12
0,12
(Хi - Мх)*
(Yi-My)
305,181
249,3
108,492
25,632
20,49
232,596
322,418
129,177
0,212
(Xi-Mx)2
1426,572
1352,032
613,552
115,992
85,192
1312,612
1699,912
636,552
3,132
309 + 310 + 322 + 336 + 356 + 383 + 388 + 372 + 345
= 346,77
9
427 + 428,3 + 430,7 + 432,7 + 437,3 + 441,5 + 442,9 + 440,2 + 435,2
= 435,08
9
305,181 + 249,3 + 108,492 + 25,632 + 20,49 + 232,596 + 322,418 + 129,177 + 0,212
1426,572 + 1352,032 + 613,552 + 115,992 + 85,192 + 1312,612 + 1699,912 + 636,552 + 3,132
= 0,192
Значения у’, полученные по формуле (14):
Таблица 3
№
1
x
y
y’
у’-у
309
427
2
3
310
428,3
322
430,7
4
5
Исходные данные
336
432,7
345
435,2
6
7
8
9
356
437,3
372
440,2
383
441,5
388
442,9
Полученные значения у’
427,835 428,0276 430,331 433,019 434,747 436,859 439,931 442,043 443,003
0,835
-0,272
-0,368
0,319
-0,452
-0,440
-0,268
0,543
0,103
11
Получим график:
Вывод:
Значения у’, полученные при построении линии регрессии, отличаются от заданных во
всех девяти точках в интервале от -0,452 до 0,835. Наибольшее отклонение получилось в
первой точке – у1’-у1 = 0,835; наименьшее в последней – у9’-у9 = 0,103.
Тема 2. Теория погрешностей и практика их оценки
Работа №5
Задание:
Определить доверительный интервал неисключенного остатка систематической
составляющей неопределенности, случайной составляющей и доверительный интервал
общей неопределенности результата измерения коэффициента теплопроводности 
материала. Исходные данные представлены в таблицах:
Метрологические характеристики измерительных приборов
Амперметр
Вольтметр
Мост
Тепломер Термометр сопротивл.
Вариант
Кл.
Пред.
Кл.
Пред.
Кл.
Кл.
R0, Ом
10-3, 1/К
8
0,05
2,5 А
0,1
50 В
0,02
2,5
900,0011 4,90,0025
Примечание:
1.
Кл. – класс точности прибора в %.
2.
Пред. – верхний предел измерения.
3.
Неисключенный остаток систематической составляющей погрешности измерения
силы тока I, A и напряжения U, В определяется умножением верхнего предела измерения
прибора на класс точности, выраженный в долях. Например, для силы тока, измеряемой
прибором с классом точности 0,16 и верхним пределом измерения 2,0 А, величина
неисключенного остатка систематической погрешности будет равна:
θI = 2*0,16/100=0,0032 А.
12
4.
Для моста сопротивления и тепломера неисключенный остаток систематической
погрешности определяется умножением показания прибора на класс точности,
выраженный в долях.
5.
Значения α, представленные в табл., необходимо разделить на 103.
Вариант
8
Показания измерительных приборов при измерении первой точки
Амперметр,
Вольтметр,
Тепломер, Мост сопротивления,
L,
I н, А
Uн, В
q, Вт
м-1
Rt1, Ом
Rt2, Ом
2,31
43,8
0,77
134,12
132,53
44,240,029
Результаты экспериментального исследования
коэффициента теплопроводности
Номер Значения
точки
 i,
мВт/(мК)
6
i
1
Расч.
2
275,5
3
277,4
4
277,1
5
276,3
6
276,8
7
277,2
8
277,9
9
278,5
10
278,4
11
279,6
12
279,9
Решение:
Коэффициент теплопроводности материала измеряется методом коаксиальных цилиндров.
Принцип измерения заключается в нагреве системы из трех цилиндрических образцов
коаксиальным тепловым потоком заданной величины. Исследуемый образец помещают
между образцами с известными свойствами. Вычисление коэффициента
теплопроводности исследуемого образца осуществляют с помощью температурных
градиентов, возникающих в трех цилиндрах. Принципиальная схема установки показана
на рисунке А1.
13
Рис. 1. Принципиальная схема установки для измерения коэффициента теплопроводности
веществ методом коаксиальных цилиндров: 1 – термостат; 2 – наружный цилиндр; 3 –
внутренний цилиндр; 4 – слой исследуемого вещества; 5 – электрический нагреватель; 6, 7
– термометры сопротивления; 8 – тепломер; R – мост сопротивления; A – амперметр; V вольтметр.
Для измерения коэффициента теплопроводности необходимо измерить мощность
электрического нагревателя и разность температур в слое исследуемого вещества.
Рабочая формула метода имеет вид:
𝑄−𝑞
=
,
(1)
𝐿𝑇
где Q – мощность нагревателя, Вт, определяется путем измерения тока Iн с помощью
амперметра A и падения напряжения на нагревателе Uн - с помощью вольтметраV: Q =
UнIн; q – мощность теплового потока, улавливаемая тепломером с торцов цилиндров, Вт;
L – постоянная прибора, определяемая экспериментально-расчетным методом, м-1; T = t1
– t2 – разность температур в слое жидкости, определяемая с помощью двух одинаковых
термометров сопротивления 6 и 7; t1, t2 – значения температуры, определяемые
соответственно термометрами 6 и 7.
Так как по условиям задачи термометры изготовлены из одной партии платиновой
проволоки и имеют одинаковые значения сопротивления R0, то формула (1)
примет вид:
(𝑈н 𝐼н − 𝑞)𝑅0 
=
,
(2)
𝐿(𝑅𝑡1 − 𝑅𝑡2 )
Определим значение  в точке 1:
=
(43,8 ∗ 2,31 − 0,77) ∗ 90 ∗ 4,9 ∗ 10−3
44,24 ∗ (134,12 − 132,53)
= 629,4 мВт/(мК)
Номер измерения
Результаты экспериментального измерения
коэффициента теплопроводности
Результат, i,
𝑌 = (̅ − ), i,
14
𝑌̃𝑖 = (̅ − )/̅
мВт/(мК)
629,4
275,5
277,4
277,1
276,3
276,8
277,2
277,9
278,5
278,4
279,6
279,9
307
1
2
3
4
5
6
7
8
9
10
11
12
Среднее (̅̅̅
)
мВт/(мК)
-322,4
31,5
29,6
29,9
30,7
30,2
29,8
29,1
28,5
28,6
27,4
27,1
-1,05
0,102
0,096
0,097
0,1
0,098
0,097
0,094
0,092
0,093
0,089
0,088
Зная метрологические характеристики приборов, определяем величину доверительного
интервала неисключенного остатка систематической погрешности i:
- 𝑈𝑁 = 500,1/100 = 0,05 В;
- 𝐼𝑁 = 2,50,1/100 = 0,0025 А;
- 𝑞 = 100,0005 = 0,005 Ом;
- 𝑅0 = 0,0011 Ом;
-  = 2,510-6 К-1;
- 𝐿 = 0,774/100 = 0,0308 м-1;
- 𝑅𝑡1 = 134,120,1/100 = 0,13412 Ом;
- 𝑅𝑡2 = 132,530,1/100 = 0,13253 Ом.
Дифференцируя рабочую формулу (2) по всем переменным получим формулы для
вычисления коэффициентов влияния 𝑏̃𝑖 – уравнения:
𝑏𝑈н =
𝜕
𝑅0 ∗ 𝐼𝐻 ∗ 𝛼
90 ∗ 2,31 ∗ 4,9 ∗ 10−3
=
=
= 0,01447
𝜕𝑈н (𝑅𝑡1 − 𝑅𝑡2 ) ∗ 𝐿 (134,12 − 132,53) ∗ 44,24
1

𝑏̃𝑈н =
=
1
= 1,588
629,4 ∗ 10−3
1 𝜕
= 1,588 ∗ 0,01447 = 0,0229
 𝜕𝑈н
𝜕
𝑅0 ∗ 𝑈𝐻 ∗ 𝛼
90 ∗ 43,8 ∗ 4,9 ∗ 10−3
𝑏𝐼н =
=
=
= 0,274
𝜕𝐼н (𝑅𝑡1 − 𝑅𝑡2 ) ∗ 𝐿 (134,12 − 132,53) ∗ 44,24
𝑏̃𝐼н =
𝑏𝑞 =
1 𝜕
= 1,588 ∗ 0,274 = 0,435
 𝜕𝐼н
𝜕
𝑅0 ∗ 𝛼
90 ∗ 4,9 ∗ 10−3
=
=
= 0,00626
𝜕𝑞 (𝑅𝑡1 − 𝑅𝑡2 ) ∗ 𝐿 (134,12 − 132,53) ∗ 44,24
15
𝑏̃𝑞 =
𝑏𝑅0 =
𝜕
𝛼 ∗ (𝐼𝐻 ∗ 𝑈𝐻 − 𝑞) 4,9 ∗ 10−3 ∗ (2,31 ∗ 43,8 − 0,77)
=
=
= 0,00698
(𝑅𝑡1 − 𝑅𝑡2 ) ∗ 𝐿
(134,12 − 132,53) ∗ 44,24
𝜕𝑅0
𝑏̃𝑅0 =
𝑏 =
𝑏𝐿 =
1 𝜕
= 1,588 ∗ 0,00626 = 0,0099
 𝜕𝑞
1 𝜕
= 1,588 ∗ 0,00698 = 0,0110
 𝜕𝑅0
𝜕 𝑅0 ∗ (𝐼𝐻 ∗ 𝑈𝐻 − 𝑞)
90 ∗ (2,31 ∗ 43,8 − 0,77)
=
=
= 128,46
(𝑅𝑡1 − 𝑅𝑡2 ) ∗ 𝐿
(134,12 − 132,53) ∗ 44,24
𝜕
1 𝜕
𝑏̃ =
= 1,588 ∗ 128,46 = 203,99
 𝜕
𝜕 𝛼 ∗ 𝑅0 ∗ (𝐼𝐻 ∗ 𝑈𝐻 − 𝑞) 4,9 ∗ 10−3 ∗ 90 ∗ (2,31 ∗ 43,8 − 0,77)
=
=
= 0,0142
𝜕𝐿
𝐿2 ∗ (𝑅𝑡1 − 𝑅𝑡2 )
44,242 ∗ (134,12 − 132,53)
𝑏̃𝐿 =
𝑏𝑅1
1 𝜕
= 1,588 ∗ 0,0142 = 0,0225
 𝜕𝐿
𝜕
𝑅0 ∗ 𝛼 ∗ (𝐼𝐻 ∗ 𝑈𝐻 − 𝑞) 90 ∗ 4,9 ∗ 10−3 ∗ (2,31 ∗ 43,8 − 0,77)
=
=
=
= 0,395
𝜕𝑅1
(𝑅𝑡1 − 𝑅𝑡2 )2 ∗ 𝐿
(134,12 − 132,53)2 ∗ 44,24
𝑏̃𝑅1 =
𝑏𝑅2 =
1 𝜕
= 1,588 ∗ 0,395 = 0,628
 𝜕𝑅1
𝜕
𝑅0 ∗ 𝛼 ∗ (𝐼𝐻 ∗ 𝑈𝐻 − 𝑞) 90 ∗ 4,9 ∗ 10−3 ∗ (2,31 ∗ 43,8 − 0,77)
=
=
= 0,395
𝜕𝑅2
(𝑅𝑡1 − 𝑅𝑡2 )2 ∗ 𝐿
(134,12 − 132,53)2 ∗ 44,24
𝑏̃𝑅2 =
2
2
1 𝜕
= 1,588 ∗ 0,395 = 0,628
 𝜕𝑅2
2
2
2
2
2
2
̃ 𝑡 = 𝑘√𝑏̃𝑈н 2𝑈н + 𝑏̃𝐼н 2𝐼н + 𝑏̃𝑞 2𝑞 + 𝑏̃𝑅0 2𝑅0 + 𝑏̃ 2 + 𝑏̃𝐿 2𝐿 + 𝑏̃𝑅1 2𝑅1 + 𝑏̃𝑅2 2𝑅2
̃ 𝑡 =
2
1,1√0,0229 0,052 + 0,4352 0,00252 + 0,0992 0,0052 + 0,0112 0,00112 + 203,92 0,0000022 +
0,03082 0,02252 + 0,6282 0,134122 + 0,6282 0,132532 = 0,1302
Для оценки случайной составляющей погрешности результата измерения температуры в
течение опыта определяем величину СКО отдельного измерения.
∑𝑛 𝑌̃ 2
𝑆̃𝑌𝑖 = √ 𝑖=1 𝑖
𝑛−1
16
𝑛
∑ 𝑌̃𝑖2 = 1,052 +0,1022 +0,0962 +0,0972 +0,12 + 0,0982 + 0,0972 + 0,0942 + 0,0922
𝑖=1
+ 0,0932 +0,0892 +0,0882 = 1,202136
∑𝑛𝑖=1 𝑌̃𝑖2
1,202136
√
̃
𝑆𝑌𝑖 =
=√
= 0,3305
𝑛−1
12 − 1
для среднего результата:
∑𝑛𝑖=1 𝑌̃𝑖2
1,202136
=√
= 0,095
𝑛(𝑛 − 1)
12 ∗ (12 − 1)
𝑆̃𝑌̅𝑖 = √
Доверительный интервал случайной составляющей погрешности для среднего результата
измерения температуры в течение опыта определяется по формуле:
𝛹 = 𝑡𝑞 𝑆̃𝑌̅𝑖 ,
где tq – коэффициент распределения Стьюдента. При числе измерений n = 12 и
доверительной вероятности p = 0,95; tq = 2,20.
Ψ = 2,20*0,095 = 0,209
Тогда доверительный интервал неопределенности измерения средней температуры опыта
вычисляется по формуле
2
1
𝑌̃ = 𝑘√𝑘 2 ̃ 𝑌̅ + 𝛹 2 ,
где ̃ 𝑌̅ = ̃ 𝑡 .
1
0,13022 + 0,2092 = 0,2399
1,12
𝑌̃ = 1,1√
Доверительный интервал неопределенности измерения среднего коэффициента
теплопроводности опыта составит 23,9% Столь высокое значение получается из-за
величины доверительного интервала неисключенного остатка систематической
погрешности моста сопротивления. Произведение этой величины на коэффициент
влияния составляет:
̃ 𝑡 = 1,1 ∗ √0,6282 0,134122 + 0,6282 0,132532 = 0,1302
Вывод:
Разобрал принцип расчета доверительного интервала неисключенного остатка
систематической составляющей неопреленности, случайной составляющей и
доверительного интервала общей неопределенности применительно к значениям
коэффициента теплопроводности, полученным путем экспериментального исследования
(методом коаксиальных цилиндров).
Тема 3. Основы математического анализа результатов
экспериментального исследования
Работа №6
Построение линейной зависимости регрессии
Задание:
17
Построить линейную зависимость регрессии по экспериментальным точкам, значения
которых приведены в предыдущем задании (работа №3, табл. 1). Получить уравнение
регрессии, построить в одной системе координат эмпирическую и теоретическую линии.
Решение:
Таблица 1
№
Расход,
кг/час, (х)
Тепловой
поток,
Вт/м2, (у)
1
Расположим исходные данные в порядке возрастания:
2
3
4
5
6
7
8
9
307
310
322
334
345
356
372
381
388
426,8
428,3
430,7
432,5
435,2
437,3
440,2
441,3
442,9
Получим график:
440
438
436
434
Исходные данные
432
430
428
426
305
315
325
335
345
355
365
375
Для линейной зависимости линия регрессии задается уравнением прямой,
,
(13)
неизвестные коэффициенты определяются по методу наименьших квадратов. В
соответствии с этим методом, квадрат расстояния по вертикали между опытными точками
с координатами xi,yi и соответствующими точками на линии регрессии должно быть
минимальным.
Уравнение регрессии принимает вид:
(14)
где
18
(15)
(16)
Результаты вычислений:
Таблица 2
Признаки
№
Xi
Yi
1
2
3
4
5
6
7
8
9
М𝑥 =
М𝑦 =
39,11
36,11
24,11
12,11
9,89
34,89
41,89
25,89
1,11
8,22
6,72
4,32
2,52
2,28
6,28
7,88
5,18
0,18
(Xi-Mx)2
1529,592
1303,932
581,292
146,652
97,812
1217,312
1754,772
670,292
1,232
307 + 310 + 322 + 334 + 356 + 381 + 388 + 372 + 345
= 346,11
9
321,484 + 242,659 + 104,155 + 30,517 + 22,549 + 219,109 + 330,093 + 134,11 + 0,2
1529,6 + 1303,9 + 581,3 + 146,7 + 97,8 + 1217,3 + 1754,8 + 670,3 + 1,2
Таблица 3
№
1
y’
у’-у
426,8
428,3
430,7
432,5
437,3
441,3
442,9
440,2
435,2
(Хi - Мх)*
(Yi-My)
321,484
242,659
104,155
30,517
22,549
219,109
330,093
134,11
0,2
426,8 + 428,3 + 430,7 + 432,5 + 437,3 + 441,3 + 442,9 + 440,2 + 435,2
= 435,02
9
𝛽=
x
y
307
310
322
334
356
381
388
372
345
Хi - Мx Уi- Му
= 0,192
Значения у’, полученные по формуле (14):
3
4
5
6
7
8
9
Исходные данные
307
310
322
334
345
356
372
381
388
426,8
428,3
430,7
432,5
435,2
437,3
440,2
441,3
442,9
Полученные значения у’
427,510 428,087 430,391 432,695 434,807 436,919 439,991 441,719 443,063
0,711
-0,213
-0,309
0,195
-0,393
-0,381
-0,209
0,419
0,163
2
Получим график:
19
444
442
440
438
436
Исходные
данные
Линия
регрессии
434
432
430
428
426
305
325
345
365
385
Вывод:
Значения у’, полученные при построении линии регрессии, отличаются от заданных во
всех девяти точках в интервале от -0,309 до 0,711. Наибольшее отклонение получилось в
первой точке – у1’-у1 = 0,711; наименьшее в последней – у9’-у9 = 0,163.
Тема 4. Обработка результатов измерений
Работа №7
Задание:
1. Средствами Excel «Поиск решения» выполнить аппроксимацию массива данных,
представленных в табл. 2 нелинейными уравнениями, представленными в табл. 1.
2. Выполнить анализ на наличие «промахов» и определить эмпирический
коэффициент корреляции.
3. Для данного массива выполнить аппроксимацию встроенными функциями пакета
Excel «Линия тренда» и сравнить полученные двумя методами результаты.
4. Построить график зависимости.
Вариант
6
Таблица 1. Формы уравнений и первые приближения
Форма уравнения
Предлагаемые первые приближения
𝐴1
2 + 𝑛1

A1= 3.5; A2= 3.2; N1= 1.5; N2= 3.7; Tc= 420
𝑌 = 𝑒𝑥𝑝 [
]
1 + 𝐴2 ∗ 𝑛2
Таблица 2. Массивы данных для аппроксимации по вариантам
i
1
2
3
4
5
6
7
Вариант 6
8
20
9
10
11
12
13
14
15
T, K
P,
Мпа
260
381,5
280
135,4
300
59,87
320
28,71
340
15,99
360
9,709
380
6,558
400
4,851
420
3,739
440
2,963
460
2,495
480
2,159
500
1,951
520
1,765
Решение:
Средствами Excel «Поиск решения» несколько раз выполним аппроксимацию массива
данных, после чего получим окончательные значения:
Таблица 3. Массив данных после аппроксимации
𝐴1
𝐴1
2 + 𝑛1
2 + 𝑛1


𝑌 = 𝑒𝑥𝑝 [
] 𝑌 ′ = (𝑃 − 𝑒𝑥𝑝 [
])2
1 + 𝐴2 ∗ 𝑛2
1 + 𝐴2 ∗ 𝑛2
i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
381,4625
135,8036
58,74886
29,33331
16,37644
10,02138
6,632473
4,699374
3,533371
2,796083
2,310724
1,979997
1,747872
1,580758
1,457789
Сумма
0,001403451
0,162905591
1,256952234
0,388517821
0,149335936
0,097584067
0,005546264
0,022990529
0,042283175
0,027861306
0,033957664
0,032041921
0,041261111
0,033944975
0,021671129
2,318257
Определим эмпирический коэффициент корреляции:
Среднее для Y = 𝑥̅ = 400; для Y' = 𝑦̅ = 43,951
Таблица 4. Значения для расчета коэффициента корреляции
𝑥𝑖 − 𝑥̅
𝑦𝑖 − 𝑦̅
(𝑥𝑖 − 𝑥̅ ) ∙ (𝑦𝑖 − 𝑦̅)
(𝑥𝑖 − 𝑥̅ )2
(𝑦𝑖 − 𝑦̅)2
-140
-120
-100
-80
-60
-40
-20
0
20
40
60
80
100
337,549
91,449
15,919
-15,241
-27,961
-34,242
-37,393
-39,1
-40,212
-40,988
-41,456
-41,792
-42
-47256,86
-10973,88
-1591,9
1219,28
1677,66
1369,68
747,86
0
-804,24
-1639,52
-2487,36
-3343,36
-4200
19600
14400
10000
6400
3600
1600
400
0
400
1600
3600
6400
10000
113939,3
8362,92
253,4146
232,2881
781,8175
1172,515
1398,236
1528,81
1617,005
1680,016
1718,6
1746,571
1764
21
540
1,605
120
-42,186
140
-42,346
Сумма
𝑅=
-5062,32
-5928,44
-78273,4
∑(𝑥𝑖 − 𝑥̅ )(𝑦𝑖 − 𝑦̅)
√∑(𝑥𝑖 − 𝑥̅ )2 √∑(𝑦𝑖 − 𝑦̅)2
14400
19600
112000
=
−78273,4
√112000√139768,4
1779,659
1793,184
139768,4
= −0,6256
Построим график с нанесением исходных данных, данных полученных после
аппроксимации, и степенной линии тренда:
400
350
Эксперементальная
зависимость
300
250
Аппроксимирующая
функция
200
150
Степенная
(Эксперементальная
зависимость)
100
50
0
225
275
325
375
425
475
Вывод:
22
525
При сравнении исходных значений P, и полученных значений Y, наибольшая разница
между результатами наблюдается в точке i = 4, эта разница равна 1,121. В остальных же
точках разница между значениями колеблется от -0,404 до 0,206.
Однако, наибольшее отклонение от исходных и аппроксимированных данных имеют
значения полученные степенной линией тренда, вызвано это тем, что линия тренда
строится с большим радиусом округления, поэтому сходимость результатов начинается с
точки i = 3.
Тема 5. Аналитические методы
Работа №8
Расчет термодинамических свойств с использованием кубического уравнения состояния
Задание:
Выполнить расчет плотности вещества по уравнению состояния П-Р при
температуре и давлении, указанных в таблице 1. Сравнить со справочными значениями.
Таблица 1. Исходные данные для расчета плотности
№ Вещество
Tc, K
Pc, Мпа

6
Бензол
594,55
2,281
0,4433
P, МПа
2,4537
T, K
360
600
, моль/л
10,360
0,579
Решение:
Определим константы: 𝑎 = 0,45724𝑅2
2
𝑎 = 0,45724 ∗
594,55
8,3142
2281
594,55
𝑏 = 0,07780 ∗ 8,314
2281
𝑇𝑐2
𝑝𝑐
𝑇
, 𝑏 = 0,07780𝑅 𝑐 ,
𝑝𝑐
=4897,965
=0,1686
2
𝛼 = [1 + (0,37464 + 1,542261𝜔 − 0,26992𝜔2 )(1 − 𝑇𝑟0,5 )] ,
Tr = T/Tc = 360/594,55 = 1,076
Рr = Р/Рc = 2453,7/2281 = 0,6055
2
𝛼 = [1 + (0,37464 + 1,542261 ∗ 0,4433 − 0,26992 ∗ 0,44332 )(1 − 1,0760,5 )] = 1,496
Все КУС приводятся к канонической форме:
𝑍 3 + 𝑆𝑍 2 + 𝑇𝑍 + 𝑄 = 0,
где Z = pV/(RT) – коэффициент сжимаемости.
Для уравнения П-Р:
𝑃𝑟
0,6055
𝐴 = 0.45724 2 = 0,45724 ∗ 1,496 ∗
= 2,0067
𝑇𝑟
1,0762
𝑃𝑟
0,6055
𝐵 = 0.07780 = 0.07780
= 0,1382
𝑇𝑟
1,076
𝑆 = −(1 − 𝐵) = −(1 − 0,1382) = −0,8618
𝑇 = 𝐴 − 3𝐵2 − 2𝐵 = 2,007 − 3 ∗ 0,13822 − 2 ∗ 0,1382 = 1,6730
𝑄 = 𝐴 ∗ 𝐵 − 𝐵2 − 𝐵3 = 2,0067 ∗ 0,1382 −0,13822 −0,13823 = −0,2556
Построим график по полученному уравнению в интервале 1;-1:
Z
𝑍 3 − 0,8618𝑍 2 + 1,6730𝑍 − 0,2556 = 0
23
-1,0
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1,0
-3,79
-2,66
-1,79
-1,13
-0,63
-0,26
0,05
0,34
0,65
1,04
1,56
2
1
0
-1,5
-1
-0,5
0
0,5
1
1,5
0,5
1
1,5
-1
-2
-3
-4
-5
Решим кубическое уравнение:
𝑍 3 − 0,8618𝑍 2 + 1,6730𝑍 − 0,2556 = 0
Z = 0,164
Определим объем и плотность:
V = Z*R*T/P = 0,164*8,314*360/2453,7 = 0,2 м3
ρ = 1/V = 5,0 кг/м³
Если Т = 600К:
0,5
0
-1,5
-1
-0,5
0
-0,5
-1
-1,5
-2
-2,5
24
𝑍 3 − 0,917069763𝑍 2 + 0,292040986𝑍 − 0,032237145 = 0
Z = 0,3137
V = Z*R*T/P = 0,3137*8,314*600/2453,7 = 0,6378 м3
ρ = 1/V = 1,57 кг/м³
Вывод:
Выполнил расчет плотности вещества по уравнению состояния Пенга - Робинсона при
заданных параметрах с помощью коэффициента сжимаемости.
Работа №9
Построение прогнозов с использованием возможностей Microsoft Excel
Задание
Имеются статистические данные за несколько лет о дефектах системы теплоснабжения
района. Необходимо, используя статистические методы, рассчитать прогнозное значение
интересующего показателя на следующий год, т.е. на будущий период. Кроме того,
необходимо проанализировать имеющиеся данные и найти закономерность их изменения
во времени. Таким образом, задание сводится к следующим этапам:
1) По приведенным данным необходимо построить прогноз с использованием скользящей
средней, функции роста и тенденции. Построить графики с прогнозными данными и
сравнить их с фактическими.
2) Найти наиболее точную форму зависимости между статистическими данными и
временем, а также определить вид этой зависимости и ее точность, используя
коэффициент детерминации R2. Используя уравнение регрессии, найти значение
исследуемого показателя в будущем периоде.
Исходные данные 8 Вариант
Период
1
2
3
4
5
6
Данные
302
257
256
281
296
267
Период
7
8
9
10
11
12
Данные
320
324
293
278
289
300
По исходным данным построить графики прогнозов с использованием функций
Скользящая Средняя, Тенденция, Рост. Для исходных данных подобрать уравнение
регрессии с коэффициентом детерминации R2 наиболее близким к единице. Сделать
прогноз на будущий период по выбранному уравнению регресии.
25
Таким образом, можно сделать вывод, что в зависимости от используемого метода
прогнозирования прогнозное значение исследуемого показателя в будущем периоде будет
равняться: 289 для средней скользящей, 302,6 – при использовании функции тенденции,
302,7 – при использовании функции роста.
26
27
Для того, чтобы определить форму и вид зависимости между имеющимися
статистическими данными и фактором времени необходимо построить график данных,
который показывает изменение изучаемого показателя во времени (в динамике).
В данном случае наиболее точно развитие исследуемого процесса в динамике отображает
полиномиальная зависимость 6й степени. Коэффициент детерминации наиболее близок к
единице и равен 0,788, а уравнение регрессии имеет следующий вид:
y = 0,1426x4 - 3,9449*x3 + 36,254*x2 – 120,78*x + 388,36
Подставив в данное уравнение значение будущего периода (триннадцатого), получим
прогнозное значение:
y = 0,1426*134 – 3,9449*133 + 36,254*132 – 120,78*13 + 388,36 =347,9⟹348
Вывод : На 13ый период количество дефектов в районе теплоснабжения составит 348 шт.
Работа №10
Применение теории подобия в тепловых расчетах
Задание
Определить средние коэффициенты теплоотдачи и передачу теплоты при свободной
конвекции от вертикальной гладкой поверхности отопительных приборов с высотами Н =
200, 400, 600 и 800 мм и длиной L=1400 мм к воздуху. Температура стенки прибора
Тст = 85 оС, температура воздуха Тпот = 20оС. Построить график зависимости
коэффициента теплоотдачи от высоты прибора. Порядок решения задачи:
1.
Вычислить числа Грасгофа по формуле, при этом выбрать параметры сухого
воздуха для температуры Тпот = 20оС, а характерный размер принять равным высоте
прибора, т.е. расчет этого числа выполнить четыре раза для Н = 200, 400, 600 и 800 мм.
Все расчеты выполнять в системе СИ.
2.
Вычислить четыре раза числа Рэлея, приняв число Прандтля Pr для сухого воздуха
при Тпот = 20оС.
3.
Вычислить по формуле числа Нуссельта, приняв значения коэффициентов С и n в
этом уравнении в зависимости от чисел Рэлея по таблице.
28
4.
Из формулы (22) получить значение коэффициентов теплоотдачи α для заданных
высот приборов.
5.
Определить мощность отопительного прибора Q = α* H*L*( Tст - Тпот)
Решение
𝑏∗𝑔∗𝑙 3 ∗∆𝑇
1. Вычислить числа Грасгофа 𝐺𝑟 =
для разных высот прибора.
𝑣2
Коэффициент кинематической вязкости v= 15,06*10-6 при Тпот = 20оС.
Температурный коэффициент объемного расширения теплоносителя
1
𝑏=
= 3,41 ∗ 10−3 при Тпот = 20оС.
0
273+t C
𝐺𝑟 =
𝐺𝑟 =
𝐺𝑟 =
𝐺𝑟 =
3,41∗10−3 ∗9,81∗0,23 ∗(85−20)
(15,06∗10−6 )2
−3
3,41∗10 ∗9,81∗0,43 ∗(85−20)
(15,06∗10−6 )2
−3
3,41∗10 ∗9,81∗0,63 ∗(85−20)
(15,06∗10−6 )2
−3
3,41∗10 ∗9,81∗0,83 ∗(85−20)
(15,06∗10−6 )2
= 76,7 ∗ 106 - для прибора 200 мм
= 613,6 - для прибора 400 мм
= 2070,8 ∗ 106 - для прибора 600 мм
= 4908,6 ∗ 106 - для прибора 800 мм
2. Вычислить числа Рэлея Ra = Gr.Pr , где Pr = 0,703
Ra = Gr ∗ Pr = 76,7 ∗ 106 ∗ 0,703 = 53,9 ∗ 106 -для прибора 200 мм
Ra = Gr ∗ Pr = 613,6 ∗ 106 ∗ 0,703 = 431,3 ∗ 106 -для прибора 400 мм
Ra = Gr ∗ Pr = 2070,8 ∗ 106 ∗ 0,703 = 1455,7 ∗ 106 -для прибора 600 мм
Ra = Gr ∗ Pr = 4908,6 ∗ 106 ∗ 0,703 = 3450,7 ∗ 106 -для прибора 800 мм
𝑛
3. Вычислить числа Нуссельта 𝑁𝑢пот = 𝐶 ∗ 𝑅𝑎пот
при C=0,135 и n=1/3
1
𝑁𝑢пот = 0,135 ∗ (53,9 ∗ 106 )3 = 50,69 – для прибора 200 мм
1
𝑁𝑢пот = 0,135 ∗ (431,3 ∗ 106 )3 = 101,32 – для прибора 400 мм
1
𝑁𝑢пот
= 0,135 ∗ (1455,7 ∗ 106 )3 = 151,9 – для прибора 600 мм
1
𝑁𝑢пот = 0,135 ∗ (3450,7 ∗ 10
6 )3
= 202,5 – для прибора 800 мм
4. Коэффициент теплоотдачи α из формулы 𝑁𝑢 =
α=
α=
α=
α=
Nu∗λ
l
Nu∗λ
l
Nu∗λ
l
Nu∗λ
l
=
=
=
=
50,69∗2,59∗102
= 9377
1,4
101,32∗2,59∗102
1,4
151,9∗2,59∗102
1,4
202,5∗2,59∗102
1,4
Вт
м2 ∗℃
Вт
= 18744
= 37462,5
λ
-для прибора 200 мм
м2 ∗℃
Вт
= 28101,5
α∗l
м2 ∗℃
Вт
м2 ∗℃
-для прибора 400 мм
-для прибора 600 мм
-для прибора 800 мм
5. Определить мощность отопительного прибора Q = α* H*L*(Tст - Тпот)
Q = 9377* 0,2*1,4 *( 85 - 20)= 170,6 кВт –для прибора 200 мм
Q = 18744* 0,4*1,4*( 85 - 20)= 682,3 кВт –для прибора 400 мм
Q = 28101,5* 0,6*1,4*( 85- 20)= 1534,3 кВт –для прибора 600 мм
Q =37462,5* 0,8*1,4*( 85 - 20)= 2727,3 кВт –для прибора 800 мм
29
График зависимости коэффициента теплоотдачи α от высоты прибора Н
Ряд 1
40000
35000
30000
25000
20000
15000
10000
5000
0
0,2
0,4
0,6
0,8
Ряд 1
Вывод: Коэффициент теплоотдачи прибора прямолинейно зависит от высоты этого
прибора.
Работа № 11
Вариант № 4
Задание
Задан диапазон изменения факторов (температура T и давление P, табл. 11.1) и
результаты полного факторного эксперимента (табл. 11.2) оптимизации функции Y(T,P).
Составить матрицу ПФЭ, определить коэффициенты регрессии, произвести анализ
однородности дисперсии параллельных опытов, определить ошибку всего эксперимента,
проверить значимость коэффициентов регрессии, проверить адекватность модели.
Вычислить значение искомой функции при заданных P и T (табл. 11.1).
Таблица 11.1. Диапазон изменения факторов и параметры расчета свойства
Вариант
T1, ºC
T2, ºC
P1, МПа
P2, МПа
T, ºC
6
-24
48
2
22
12,8
Таблица 11.2. Результаты полного факторного эксперимента
№
X1
X2
1
-
-
2
+
-
3
-
+
4
+
+
30
Y
64,21
64,82
65,12
97,98
98,42
98,61
68,13
68,54
68,88
76,83
P, МПа
15,6
77,25
77,47
1. Рассчитывается среднее значение 𝑌̅𝑖
64,21 + 64,82 + 65,12
= 64,77
3
97,98 + 98,42 + 98,61
𝑌̅2 =
= 98,33
3
68,13 + 68,54 + 68,88
𝑌̅3 =
= 68,51
3
76,83 + 77,25 + 77,47
𝑌̅1 =
= 77,18
3
𝑌̅1 =
2. Производится анализ однородности дисперсии параллельных опытов.
2.1. Вычисляется оценка дисперсий 𝑆𝑖2 (𝑌𝑖 )
𝑛
𝑆𝑖2 (𝑌𝑖 )
1
=
∑(𝑌𝑖𝑗 − 𝑌̅𝑖 )2
𝑛−1
𝑗=1
1
∙ ((64,21 − 64,77)2 + (64,82 − 64,77)2 + (65,12 − 64,77)2 ) = 0,219
3−1
1
𝑆22 (𝑌2 ) =
∙ ((97,98 − 98,33)2 + (98,42 − 98,33)2 + (98,61 − 98,33)2 ) = 0,254
3−1
1
𝑆32 (𝑌3 ) =
∙ ((68,13 − 68,51)2 + (68,54 − 68,51)2 + (68,88 − 68,51)2 ) = 0,141
3−1
1
𝑆42 (𝑌4 ) =
∙ ((76,83 − 77,18)2 + (77,25 − 77,18)2 + (77,47 − 77,18)2 ) = 0,256
3−1
𝑆12 (𝑌1 ) =
2.2. Рассчитывается критерий Кохрена 𝐺расч
𝐺расч =
𝐺расч =
2
𝑆𝑚𝑎𝑥
2
∑𝑁
𝑖=1 𝑆𝑖
0,256
= 0,294
0,219 + 0,254 + 0,141 + 0,256
2.3. По таблице определяется 𝐺табл при числе степеней свободы 𝑓1 = 2 и при
уровне значимости 𝑔 = 0,05 (доверительной вероятности 0,95)
𝐺табл = 0,9750
2.4. Сравнивается расчетное и табличное значение критерия Кохрена
𝐺расч < 𝐺табл – следовательно, дисперсия однородна.
2.5. Рассчитывается критерий Фишера 𝐹расч
𝐹расч =
31
2
𝑆𝑚𝑎𝑥
2
𝑆𝑚𝑖𝑛
𝐹расч =
0,256
= 1,81
0,141
2.6. По таблице определяется 𝐹табл при числе степеней свободы 𝑓1 = 2, 𝑓2 = 4 и при
уровне значимости 𝑔 = 0,05 (доверительной вероятности 0,95)
𝐹табл = 6,94
2.7. Сравнивается расчетное и табличное значение критерия Фишера
𝐹расч < 𝐹табл – следовательно, дисперсия однородна.
3. Вычисляется ошибка всего эксперимента.
3.1. Рассчитывается дисперсия всего эксперимента 𝑆 2 (𝑌)
𝑁
1
𝑆 (𝑌) = ∑ 𝑆𝑖2
𝑁
2
𝑖=1
𝑆 2 (𝑌) =
0,219+0,254+0,141+0,256
4
=0,217
3.2. Рассчитывается ошибка всего эксперимента 𝑆(𝑌)
𝑆(𝑌) = √𝑆 2 (𝑌)
𝑆(𝑌) = √0,217 = 0,465
4. Составляется матрица ПФЭ – табл. 11.3.
Таблица 11.3. Матрица полного факторного эксперимента
№ опыта
X1
X2
X3
X1·X2
Y
1
+
-
-
+
64,77
2
+
+
-
-
98,33
3
+
-
+
-
68,51
4
+
+
+
+
77,18
5. Определяются коэффициенты регрессии 𝑏𝑖
𝑌 = 𝑏0 + 𝑏1 ∙ 𝑥1 + 𝑏2 ∙ 𝑥2 + 𝑏12 ∙ 𝑥1 ∙ 𝑥2
1
∙ (64,77 + 98,33 + 68,51 + 77,18) = 77,19
4
1
𝑏1 = ∙ (−64,77 + 98,33 − 68,51 + 77,18) = 42,23
4
1
𝑏2 = ∙ (−64,77 − 98,33 + 68,51 + 77,18) = −17,41
4
1
𝑏12 = ∙ (64,77 − 98,33 − 68,51 + 77,18) = −25,49
4
𝑏0 =
𝑌 = 77,19 + 42,23 ∙ 𝑥1 − 17,41 ∙ 𝑥2 − 25,49 ∙ 𝑥1 ∙ 𝑥2
6. Проверяется значимость коэффициентов регрессии.
6.1. Рассчитывается коэффициент ошибки 𝑆𝑏
32
𝑆𝑏 =
𝑆𝑏 =
0,465
√4 ∙ 3
𝑆(𝑌)
√𝑁 ∙ 𝑛
= 0,134
6.2. Определяется отношение абсолютного значения коэффициента регрессии к его
отклонению 𝑡𝑖
𝑡𝑖 =
𝑡0 =
|77,19|
= 576,04
0,134
𝑡1 =
|42,23|
= 315,14
0,134
𝑡2 =
|−17,41|
= 129,92
0,134
𝑡12 =
|𝑏𝑖 |
𝑆𝑏
|−25,49|
= 182,76
0,134
6.3. По таблице определяется значение критерия Стьюдента 𝑡=4,30 при числе
степеней свободы 𝑓1 = 2 и при уровне значимости 𝑔 = 0,05.
6.4. Сравнивается расчетные и табличное значения критерия 𝑡 – во всех случаях
𝑡𝑖 > 𝑡.
7. Вычисляется значение искомой функции 𝑌̂ при заданных P и T.
Значения приводятся к безразмерным величинам 𝑇 → 𝑥1 ; 𝑃 → 𝑥2 .
𝑋 − 𝑋̅
∆𝑋
𝑋2 + 𝑋1
𝑋̅ =
2
𝑋2 − 𝑋1
∆𝑋 =
2
48 − 24
48 − (−24)
12,8 − 12
𝑇̅ =
= 12; ∆𝑇 =
= 36; 𝑥1 =
= 0,02
2
2
36
22 + 2
22 − 2
15,6 − 12
𝑃̅ =
= 12; ∆𝑃 =
= 10; 𝑥2 =
= 0,36
2
2
10
𝑌̂ = 77,19 + 42,23 ∗ 0,02 − 17,41 ∙ 0,36 − 25,49 ∙ 0,02 ∗ 0,36 = 71,58
𝑥𝑖 =
8. Проверяется адекватность модели.
2
8.1. Вычисляется дисперсия адекватности 𝑆ад
𝑁
2
𝑆ад
𝑛
=
∑(𝑌̅𝑖 − 𝑌̂)2 = 0
𝑁∙𝑛−𝑙
𝑖=1
где 𝑙 – число значимых коэффициентов в уравнении регрессии.
33
Так как из четырех опытов определены четыре коэффициента уравнения регрессии,
то величина Sад=0. Расчетная линия пройдет через экспериментальные точки.
8.2. Рассчитывается критерий Фишера 𝐹расч
𝐹расч
2
𝑆ад
= 2
=0
𝑆 (𝑌)
8.3. По таблице определяется 𝐹табл при числе степеней свободы
𝑓1 = 𝑓ад = 𝑁 ∙ 𝑛 − 𝑙 = 4 ∙ 3 − 4 = 8,
𝑓2 = 𝑓воспр = 𝑁 ∙ (𝑛 − 1) = 4 ∙ (3 − 1) = 8
и при уровне значимости 𝑔 = 0,05 (доверительной вероятности 0,95)
𝐹табл = 3,44
8.4. Сравнивается расчетное и табличное значение критерия Фишера
𝐹расч < 𝐹табл – следовательно, математическое описание функции считается
адекватным.
Вывод: для заданного диапазона изменения факторов и результатов полного
факторного эксперимента оптимизации функции Y(T,P) составлена матрица ПФЭ (табл.
11.3), определены коэффициенты регрессии и проверена их значимость, определена
ошибка всего эксперимента, вычислено значение искомой функции при заданных P и T.
Дисперсия параллельных опытов однородна. Модель адекватна.
34