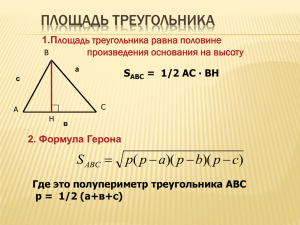
Тема урока: Решение задач по: Теореме Пифагора Формула Герона. Цель урока: вывести формулу Герона, рассмотреть ее применение при решении задач. Задачи урока: Обучающая: систематизировать и углубить знания учащихся о методах решения задач на нахождение площадей треугольника. Развивающая: развивать монологическую речь обучающихся с математическим контекстом. Воспитывающая: расширять кругозор, словарный запас и знания биографий ученых-математиков. Ход урока. 1. Организационно-мотивационный момент. Эпиграф урока «Дорогу осилит идущий, а математику - мыслящий». 2. Актуализация знаний. 3. Изучение нового материала. По готовым на доске чертежам проверить решение задач. № 490 (б). 1) ВD – высота, биссектриса и медиана по свойству равнобедренного треугольника, поэтому 1 = 2 = 60°, АD = DС = 9 см. 2) АВD –прямоугольный, 3 = 90° – 60° = 30°. 3) ВD – катет, лежащий против угла в 30°, равен половине гипотенузы, то есть АВ = 2ВD. 4) Пусть ВD = х см, тогда АВ = 2х см. По теореме Пифагора АВ2 = ВD2 + АD2, (2х)2 = х2 + 92, 4х2 = х2 + 81, 3х2 = 81, х = 3 3, АВ = 6 3 см. 1 1 5) S АВС= 2 ВD · АС = 2 3 3 · 18 = 27 3 (см2). № 490 (в). 1) СD – высота, биссектриса, медиана. АDС – равнобедренный 2) прямоугольный. По теореме Пифагора АС2 = СD2 + АD2. АС = и 72 72 = 7 2 (см). 1 1 S АВС= 2 АС · СВ = 2 · 7 2 · 7 2 = 49 (см2). Тестирование по теме « Площади многоугольников» Тест Вариант I 1. Выберите верные утверждения: а) площадь прямоугольника равна произведению двух его сторон; б) площадь квадрата равна квадрату его стороны; в) площадь прямоугольника равна удвоенному произведению двух его соседних сторон. 2. Закончите фразу: площадь ромба равна половине произведения... а) его сторон; б) его стороны и высоты, проведенной к этой стороне; в) его диагоналей. 3. По формуле S = а · hа можно вычислить площадь: а) параллелограмма; б) треугольника; в) прямоугольника. 4. Площадь трапеции ABCD с основаниями АВ и CD и высотой ВН вычисляется по формуле: а) S = АВ : 2 · CD · ВН; б) S = (АВ + BC) : 2 · ВН; в) S = (АВ + CD) : 2 · ВН. 5. Выберите верное утверждение. Площадь прямоугольного треугольника равна: а) половине произведения его стороны на какую-либо высоту; б) половине произведения его катетов; в) произведению его стороны на проведенную к ней высоту. 6. В треугольниках ABC и MNK В = N. Отношение площадей треугольников ABC и MNK равно: а) б) в) 7. В треугольниках MNK и DOS высоты NE и ОТ равны. Тогда SMNK : : SDOS = … а) MN : РО; б) МK : РS; в) NK : ОS. В а р и а н т II 1. Выберите верные утверждения: а) площадь квадрата равна произведению его сторон; б) площадь прямоугольника равна произведению его противолежащих сторон; в) площадь прямоугольника равна произведению двух его соседних сторон. 2. Закончите фразу: площадь параллелограмма равна произведению... а) двух его соседних сторон; б) его стороны на высоту, проведенную к этой стороне; в) двух его сторон. 3. По формуле S = d1 ∙ d2 : 2 можно вычислить площадь: а) параллелограмма; б) треугольника; в) ромба. 4. Площадь трапеции ABCD с основаниями ВС и AD и высотой СН вычисляется по формуле: а) S = СН · (ВC + АD) : 2; б) S = (АВ + BC) · СН : 2; в) S = (ВС + CD) · СН : 2. 7. В треугольниках DEF и TRQ высоты DA и ТВ равны. Тогда SDEF : : STRQ = … а) EF : RQ; б) DE : TR; в) EF : RT. Ответы к тесту Вариант I Вариант II 1 б в 2 в б 3 а в 4 в а 5 б б 6 а в 7 б а 4.Задача. Стороны треугольника равны 13 см, 5см, и 12 см. Найти площадь этого треугольника. Рассмотрим треугольник в котором углы острые, тогда основание высоты СД лежит на стороне АВ. Мы знакомы с формулой вычисления площадей 1 треугольников S= 2 h ∙ с Положим АD = х, тогда ВD = с – х. Применяя теорему Пифагора к треугольникам АСD и ВСD, получаем уравнения b2 = h2 + х2; а2 = h2 + (c – x)2 h2 = b2 – x2; h2 = а2 – (c – x)2 b2 – x2 = а2 – (c – x)2 b2 = а2 – c2 + 2сx b2 с 2 а 2 2с x= h2 = b2 – x2 = (b – х) (b + х) b2 с 2 а 2 b2 с 2 а 2 b b 2 с 2 с 2 h = 2bс b2 с 2 а 2 2bс b2 с 2 а 2 2 с 2 с 2 h = a 2 (b с) 2 (b с) 2 a 2 2с 2с h2 = (a b с)(а b с) (b с а )(b с а ) 2 2 с 2с h = = (2 р 2b)(2 р 2с)(2 р 2а)(2 р) 16( р b)( р с) р а р 2 4 с 4с 2 = 2 ( р b)( р с)( р а) р 1 с h= , S= 2h∙ c= р ( р а)( р b)( р с) . Эта формула носит имя Герона. А что мы знаем о Героне? 5. Закрепление изученного материала. Задача. Найти площадь треугольника со сторонами 24см,25см и 7 см. Определите наименьшую из высот треугольника. 6. Подведение итогов урока. Рефлексия. S p ( p a )( p b)( р с), р аbс . 2 7.Домашнее задание: № ________________