Задача двух тел

Небесная механика
Введение Что изучает небесная механика?
Небесная механика – это наука, которая изучает основные закономерности
механического движения небесных тел с помощью математических моделей. В рамках
классической небесной механики под термином «небесные тела» подразумеваются тела
Солнечной системы.
1) Небесную механику можно рассматривать и как часть теоретической (классической)
механики, которая занимается изучением движения любых материальных тел, и как часть
астрономии, поскольку объектами изучения небесной механики является астрономические
объекты.
2) Вся небесная механика полностью построена на известных законах физики.
3) Математические модели в небесной механике служат для исследования и описания
закономерностей реальных движений систем небесных тел. Модель есть некоторое упрощение
реальных систем. Упрощение заключается в том, что вместо бесконечного числа параметров
(некоторых характеристик), способных описать реальную систему, выбирается некоторое
конечное число параметров, важных для описания исследуемых движений. Всякая модель
отражает свойства изучаемых реальных систем лишь приближённо. Но именно упрощенные
модели реальных явлений позволяют выявить в результате их анализа основные
закономерности движений.
4) Основной математический аппарат, используемый в небесной механике для изучения
движения небесных тел – это обыкновенные дифференциальные уравнения. Динамическое
поведение материального тела или системы тел описывается в небесной механике сравнительно
небольшим числом параметров, являющихся функциями времени. Это отличительная
особенность небесной механики (так же, как и теоретической) от других механик, например, от
механики сплошной среды, где поведение системы описывается функциями многих
переменных и основным средством описания является аппарат уравнений в частных
производных.
5) Небесная механика занимается изучением физических систем, в которых время
действует непрерывно, и поведение которых во времени детерминировано. Это очень важный
фактор, обуславливающий возможность прогнозирования движения систем. Иначе говоря, для
таких систем существует правило в виде дифференциальных или других уравнений,
определяющее их будущее, исходя из заданных начальных условий. Траектория
детерминированного движения теоретически должна быть регулярной (не хаотичной),
поскольку последовательные состояния непрерывно развиваются одно из другого. (В
дальнейшем мы увидим, что это не всегда так, и вместе с регулярными траекториями могут
существовать нерегулярные, вернее, существует «порог» предсказуемости движения).
Глава 1. Постановка основной задачи небесной механики. Системы координат
1.1 Постановка задачи
Основная задача небесной механики – изучение движения материальной системы,
состоящей из конечного числа свободных материальных точек, обладающих постоянными
массами и движущихся в абсолютно пустом пространстве под действием сил взаимного
притяжения, определяемых законом всемирного тяготения.
Закон всемирного тяготения Ньютона: две материальные точки P0 и P1 с массами
соответственно равными m0 и m1 , притягиваются согласно закону притяжения Ньютона с
силой, направленной по прямой P0 P1 ,
F= f
m0 m1
,
∆2
(1.1.1)
где ∆ – расстояние между точками P0 и P1 .Здесь f – коэффициент пропорциональности,
называемый постоянной притяжения (или тяготения).
Вместо f в астрономии часто употребляется другая величина, связанная с f формулой,
(1.1.2)
f = k2,
k называется постоянной Гаусса, k = 0.01720209895...
Формула (1.1.1) не зависит от выбора системы координат. Но на практике мы изучаем
движение тел в какой-либо системе координат, рассматривая составляющие (компоненты) силы
притяжения на оси этой системы.
Постановка задачи n тел. Пусть в пространстве имеется изолированная система n тел
P0 , P1 , P2 ,..., Pn −1 с массами m0 , m1, m2 ,..., mn −1 соответственно. Основная задача небесной
механики состоит в изучении движения этой материальной системы, состоящей из конечного
числа свободных материальных точек, обладающих постоянными массами и движущихся в
абсолютно пустом пространстве под действием сил взаимного притяжения, определяемых
законом всемирного тяготения (1.1.1). Более того, будем считать, что действует принцип
детерминированности, т. е. начальное состояние системы однозначно определяет ее дальнейшее
поведение. Таким образом, задача n тел заключается в нахождении вектора состояния системы
в любой момент времени при сформулированных выше условиях.
1.2 От Ньютона до Гамильтона
В рамках поставленной основной задача небесной механики модель движения
взаимодействующих тел может быть построена на основе знаменитого уравнения Ньютона
(1.2.1)
F = ma ,
связывающего ускорение движущегося тела с силой F.
С искомой траекторией движения какого-либо тела связаны такие величины, как вектор
положения тела r ( t ) (1.2.2), скорость v =
d 2r
dr
(1.2.3), и ускорение a = 2 (1.2.4).
dt
dt
Важно отметить, что время входит в уравнение Ньютона (1.2.1) только через вторую
производную. Вследствие этого уравнение Ньютона остается инвариантным при замене t на (–
t). То есть закон Ньютона обратим во времени и детерминистичен. Зная начальное
положение r ( t0 ) и начальную скорость v0, мы, интегрируя уравнение Ньютона (1.2.1), можем
найти положение r ( t ) и скорость тела r ( t ) в любой момент времени до и после t0.
Рассмотрим движение системы из n тел. Введем следующие понятия.
Опр.1. Пространство
, элементами которого являются векторы положения r ( x1 , x2 , x3 ) ,
называется конфигурационным пространством.
Опр.2. Пространство
, элементами которого являются векторы состояния
системы r ( t ) , v ( t ) , называется фазовым пространством, а совокупность координат и
компонент скорости ( x1 , x 2 , x3, x1 , x 2 , x3, ) – фазовыми координатами.
Эти два понятия лежат в основе двух различных моделей описания движения реальных
динамических систем, а именно, ньютоновское описание, называемое ньютоновой механикой,
и гамильтоново описание, называемое гамильтоновой механикой. Поясним:
В общем случае состояние динамической системы задается координатами
,
которые являются независимыми переменными, и соответствующими им скоростями
, которые являются зависимыми переменными, так как определяются как
производные от координат по времени. Именно такой подход лежит в основе ньютоновой
механики.
Современная физика использует вместо ньютоновского описания гамильтоново
описание. В гамильтоновом описании и координаты, и скорости (или, точнее, импульсы
, равные произведению массы на скорость) определяются как независимые
переменные. Преимущество такого подхода заключается в существенном упрощении
уравнений
й движени
ия. Ньютон
новская м
модель раб
ботает в конфигурац
к
ционном пространст
п
тве,
гамильтон
нова моделль – в фазовом. Ньюттоновский подход
п
госсподствоваал почти 3 столетия (18,
(
19, 20 векка). Это чи
исто детер
рминистичееский подх
ход. Класси
ическая неебесная мееханика – это
э
ньютоновсская механ
ника.
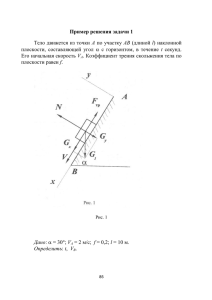
Системы координатт
Пусть задаано трехмеерное линей
йное вещесственное еввклидово пространств
п
во
(рис.. 1.1).
Элеменнты этого пространст
п
тва будем ообозначатьь r и называать
вектор ами полож
жения точ
чки, r ∈ R . Это пространсттво
будем называть абсолютн
ным прост
транством
м. Пусть O –
лютного прространстваа. Положен
ние
фиксиррованная точка абсол
произввольной то
очки в этом же просстранстве определяеттся
3
направвленным оттрезком (веектором) r = OP . Тр
ри исходящ
щие
из точки
направленные отр
резка
, взаим
мно
ортогоналльные и од
динаковой длины, обрразуют в R
3
ортонорми
ированный
й
репер
или
и
координаттный реперр декартово
ой системы
ы координатт.
Реппер E опрределяет абсолютнную систеему
3
координат
т в прострранстве R , если этта система (и
3
направлен
ние осей) остается неподвижно
н
ой в R . То
есть абссолютная система координнат – это
э
неподвижная систем
ма.
Инерциал
льные
с
системы
координ
нат.
Пуссть
∗
некоторый
й репер Eα получен из репера E путем по
оследовательных преообразовани
ий поворотта с
матрицей A и паралллельного пеереноса на вектор α
A
α
(1.3.1)
E ⎯⎯
→ E ∗ ⎯⎯
→ E α∗ .
Репер Eα∗ определяеет инерциал
льную систтему коорд
динат, если
и
1) матрица п
преобразоввания повор
рота не заввисит от вреемени
dA
= 0,
ddt
(1.3.2)
d 2α
= 0.
ddt 2
(1.3.3)
2) и ускорени
ие
Из (1.3.2) – (11.3.3) следу
ует, что реппер Eα∗ дви
ижется посступательноо, а также равномерн
р
ои
прямолинеейно относсительно E.
E Такая сисстема назыввается инер
рциальнойй системой
й координаат.
То есть ин
нерциальнаая системаа координатт движетсяя равномер
рно и прямоолинейно относитель
о
ьно
абсолютноой системы
ы координаат.
Глава 2. Задача двух тел
2.1 Дифференциальные уравнения движения в абсолютных осях
Рассмотрим движение двух материальных точек P0 и P1 под действием сил взаимного
притяжения. Выберем некоторую абсолютную прямоугольную систему координат с началом в
произвольной точке пространства О и неизменными направлениями осей. Обозначим
координаты точек Pi через (xi,yi,zi) (i=0,1). Эти координаты будут функциями времени t.
Задача. Определить 6 неизвестных (xi, yi, zi) (i=0,1) как функции одной независимой переменной
t.
Согласно II закону Ньютона F = ma, где a – ускорение, и закону всемирного тяготения силы,
действующие на точки P0 и P1, равны соответственно
F0 = m0 a0 = f
m0 m1
,
∆2
F1 = m1a1 = f
(2.1.1)
m0 m1
,
∆2
(2.1.2)
где ∆ – расстояние между точками
В уравнениях (2.1.2) и (2.1.3) запишем проекции сил на оси координат, учитывая, что
a0 =
d 2 x0
,
dt 2
a1 =
d 2 x1
,
dt 2
d 2 x0
m0 m1
mm
d 2 x1
f
(
x
x
),
.....
m
=
−
= f 0 3 1 ( x0 − x1 )
1
0
1
2
3
2
dt
dt
∆
∆
2
2
d y0
mm
mm
d y
m0
= f 0 3 1 ( y1 − y0 ), .....m1 2 1 = f 0 3 1 ( y0 − y1 ).......(2.1.3)
2
dt
dt
∆
∆
2
2
d z
mm
mm
d z
m0 20 = f 0 3 1 ( z1 − z0 ), .......m1 21 = f 0 3 1 ( z0 − z1 ).
dt
dt
∆
∆
m0
Введем обозначения
d 2x
d2y
d 2z
=
x
,
=
y
,
= z , и перепишем полученные уравнения (2.1.3) в
dt 2
dt 2
dt 2
следующем виде:
m
m1
( x1 − x0 ),...x1 = f 30 ( x0 − x1 ),
3
∆
∆
m
m
y0 = f 31 ( y1 − y0 ), ... y1 = f 30 ( y0 − y1 ),,....(2.1.4)
∆
∆
m
m
z0 = f 31 ( z1 − z0 ), ....z1 = f 30 ( z0 − z1 ).
∆
∆
x0 = f
Полученные уравнения (2.1.4) есть дифференциальные уравнения движения двух материальных
точек в абсолютных координатах.
Уравнения (2.1.4) – 12 порядка, следовательно, общее решение будет содержать 12
произвольных постоянных c1, с2,…, c12:
xi = xi (t , c1 , c2 ,..., c12 )
yi = yi (t , c1 , c2 ,..., c12 )
zi = zi (t , c1 , c2 ,..., c12 )
(2.1.6)
........(i = 0,1).
Тогда задача двух тел приводится к следующей математической задаче: определить функции
xi (t ), yi (t ), zi (t ) (i=0,1), удовлетворяющие совместно уравнениям (2.1.4) и заданным начальным
условиям, для всех значений времениt (−∞, +∞) .
2.2 Уравнения относительного движения
Можно понизить порядок системы (2.1.4), если выбрать начало координат в одной из
точек, например, в т. P0. Тогда координаты точки P0 будут равны P0 (0,0,0). А координаты точки
P1 обозначим P1 (x, y, z), так что
x = x1 − x0 , y = y1 − y0 , z = z1 − z0 (2.2.1)
Пользуясь формулами параллельного переноса (2.2.1), запишем уравнения движения (2.1.4) в
новой системе координат:
m0
m
m
x, ..... y1 = − f 30 y, .....z1 = − f 30 z
3
∆
∆
∆
m
m
m
x0 = f 31 x, ...... y0 = f 31 y, ......z0 = f 31 z.
∆
∆
∆
x1 = − f
Вычтем из первых уравнений вторые:
x
,
∆3
y
y1 − y0 = − f (m0 + m1 ) 3 ,
∆
z
z1 − z0 = − f (m0 + m1 ) 3 .
∆
x1 − x0 = − f (m0 + m1 )
..
..
..
..
..
..
..
..
..
Поскольку x1 − x0 = x, y1 − y0 = y, z1 − z0 = z и, обозначая
f (m0 + m1 ) = µ (2.2.2),
получим систему 3-х уравнений 2-го порядка, которые и представляют уравнения движения в
относительных координатах:
..
x=−
µx
r
3
..
,y=−
µy
r
3
..
,z = −
µz
r3
, (2.2.3)
где ∆ = r (r– радиус-вектор т. P1 относительно P0),
r = x 2 + y 2 + z 2 . (2.2.4)
Силовая функция U принимает вид:
U=
µ
r
, (2.2.5)
тогда уравнения движения (2.2.3) можно записать в виде
..
x=
∂U .. ∂U .. ∂U
(2.2.6)
,y=
,z =
∂x
∂y
∂z
Уравнения (2.2.3) и, соответственно уравнения (2.2.6) описывает относительное
движение одной материальной точки относительно другой, и носят название уравнений
невозмущенного кеплеровского движения.
2.3. Первые интегралы невозмущенного кеплеровского движения
Общий интеграл системы 6-го порядка (2.2.3) есть совокупность 6-и независимых между собой
первых интегралов, содержащих 6 произвольных постоянных:
.
.
.
ψ i (t , x, y, z, x, y, z, c1 ,..., c6 ) = 0, (i=1,6) .(2.3.1)
Выведем эти интегралы.
Интегралы площадей
Умножим второе из уравнений (2.2.3) на (–z), третье – на y и сложим, − yz + zy =
.
µ
r3
( yz − zy ) = 0.
.
Проинтегрируем полученное выражение: y z − z y = c1 , где c1 – произвольная постоянная.
Аналогично поступим с остальными уравнениями, в результате получим три первых интеграла:
yz − zy = c1 ,
zx − xz = c2 , .....(2.3.2)
xy − yx = c3 ,
где c1, c2, c3 – произвольные постоянные, которые могут быть найдены из начальных условий –
значений координат и компонент скорости в некоторый начальный момент времени t =t0 ,
называемый в астрономии начальной эпохой,
y0 z0 − z0 y0 = c1 ,
z0 x2 − x0 z0 = c2 , .....(2.3.3)
x0 y0 − y0 x2 = c3 ,
Интегралы (2.3.2) носят название интегралов площадей или моментов количества
движения, произвольные постоянные c1, c2, c3 обычно называются постоянными площадей.
Смысл первого названия в следующем. Запишем один из интегралов (2.3.2) в виде:
(2.3.4)
xdy − ydx = c3 dt
Левая часть выражения (2.3.4) представляет собой с точностью до малых первого порядка
удвоенную площадь dS xy элементарного треугольника, образованного на плоскости Оxy
проекциями радиус-векторов точек P′( x, y ) и P′′( x + ∆x, y + ∆y ) , соответствующих моментам
времени t и t+∆t. Площадь элементарного треугольника OP′P′′ = dS xy будет равна
dS xy =
1 x
2 x + ∆x
y
1
1
= ( x∆y − y∆x) ≈ ( xdy − ydx) .
y + ∆y 2
2
Тогда 3-е из уравнений (2.3.2) перепишется в виде 2dSxy = xdy − ydx ≅ c3dt . Интегрируя
равенство, получим S xy ≈
c3
t + c3′. Аналогичные выражения получим
2
это
для двух других
интегралов:
c3
c
c
t + c3′ , S yz ≈ 1 t + c1′ , S xz ≈ 2 t + c2′ .
(2.3.5)
2
2
2
Приближенные
равенства (2.3.5) показывают, что площади, описываемые проекциями
радиусов-векторов на координатные плоскости изменяются пропорционально времени.
Следует отметить, что соотношение (2.3.5) не являются интегралами уравнений
движения, поскольку площади Sxy, Szx, Syz не выражаются конечным образом через координаты
и компоненты скорости т. P, т.к. равенство (2.3.5) являются приближенными (с точностью до
малых первого порядка).
Смысл второго называния интегралов в следующем. Если v есть абсолютная
скорость точки P, то вектор mv есть количество движения (импульс) этой точки. Векторное
произведение [ r , mv ] , где r – вектор положения точки P, есть вектор момента количества
S xy ≈
движения или кинетический момент (момент импульса) точки P относительно начала
координат. Составляющие этого вектора суть:
{m( yz − zy ), m( zx − xz ), m( xy − yx)} или {mc1 , mc2 , mc3 } , то есть постоянные.
Следовательно, интегралы (2.3.2) показывают, что кинетический момент системы 2-х
точек есть величина постоянная во все время движения.
Плоскость Лапласа
С этими интегралами связана важная для небесной механики плоскость, так называемая
плоскость Лапласа. Вообразим себе плоскость, проходящую через начало координат системы и
определяемую уравнением
(2.3.6)
c1 x + c2 y + c3 z = 0
Очевидно, эта плоскость перпендикулярна вектору момента количества движения c (c1 , c2 , c3 ) и
остается неизменной во все время движения. Оказывается, что движение всех больших планет
Солнечной системы проходит близко к этой плоскости, которая в свою очередь близка к
плоскости эклиптики.
Интеграл энергии
Умножим уравнения (2.2.3) соответственно на x, y, z и сложим:
xx + yy + zz = −
µ
3
( xx + yy + zz ) или
1 d 2
d ⎛µ⎞
(x + y2 + z2 ) = ⎜ ⎟ .
2 dt
dt ⎝ r ⎠
r
Проинтегрировав последнее выражение, получим
2µ
µ
V2 =
+ h (2.3.8).
(2.3.7) или
x 2 + y/ 2 + z 2 = 2 + h
r
r
Мы получили еще один интеграл (2.3.7) или (2.3.8), который носит название интеграла энергии,
2µ
.
h – произвольная постоянная, которая может быть найдена из начальных условий h = V02 −
r0
Выбрав систему единиц так, чтобы масса m = 1, и учитывая, что
µ
r
= U (2.2.5), запишем (2.3.8)
V2 ⎛ µ ⎞
1
+ ⎜ − ⎟ = h . (2.3.9). Поскольку V 2 = T есть кинетическая энергия единичной
2 ⎝ r⎠
2
массы, то T+(–U)=const. Из (2.3.10) видно, что величина(–U) есть потенциальная энергия
движущейся точки, то есть (T – U) – есть полная энергия и выражение (2.3.10) говорит о том,
что полная энергия движущейся точки остается неименной во все время движения. Поэтому
интеграл (2.3.10) называется интегралом энергии, h – постоянной энергии, а функция U –
потенциалом силы притяжения.
в виде
Интегралы Лапласа
Введем следующее обозначение: rr = r ′ = xx + yy + zz.
(2.3.11)
Найдем производную r ′ :
r ′ = xx + yy + zz + x 2 + y 2 + z 2 .
Подставим сюда вместо вторых производных их выражения из уравнений (2.2.3), а вместо
квадрата скорости – выражение из интеграла энергии получим:
r′ =
µ
r
+h
(2.3.12) или
Дифференцируя это равенство и учитывая, что
соотношение
r′ = −
µr′
r′ = −
µ
r
r=−
+V 2.
(2.3.12')
xx + yy + zz r ′
= , получим следующее
r
r
.
(2.3.13)
r3
Скомбинируем каждое из уравнений (2.2.3) с уравнением (2.3.13):
r′ = −
µ r ′ × x,
r′ = −
3
µ r ′ × y,
r′ = −
3
µ r ′ × z,
r
r
r3
µx
µy
µz
x = − 3 ×( − r ′),
x = − 3 ×(− r ′),
x = − 3 ×(− r ′),
r
r
r
умножим первые 3-и уравнения на x, y, z соответственно, вторые – на −r ′ . Складывая
уравнения по координатам соответственно, получим соотношения, имеющие такую же форму,
как и для интегралов площадей:
d
xr ′ − r ′x = ( xr ′ − r ′x) = 0
dt
yr ′ − r ′y = 0
zr ′ − r ′z = 0.
Интегрируя последние три соотношения, получим:
xr′ − r ′x = l1
yr′ − r ′y = l2 ,
(2.3.14)
zr′ − r ′z = l3
где l1, l2, l3 – произвольные постоянные. Эти интегралы называются интегралами Лапласа, а
произвольные постоянные l1, l2, l3 – постоянными Лапласа.
Учитывая, что r ′ = −
µ
r
+ V 2 (2.3.12’), запишем интегралы в следующей форме:
xV 2 −
yV 2 −
µx
r
− rrx = l1
µy
− rry = l2 . (2.3.15).
r
µz
− rrz = l3
zV 2 −
r
Переходя в (2.3.15) к координатам и скоростям, получим
µx
−
+ y ( xy − yx) − z ( zx − xz ) = l1
r
µy
(2.3.16)
−
+ z ( yz − zy ) − x( xy − yx) = l2
r
µz
−
+ x( zx − xz ) − y ( yz − zy ) = l3
r
или, пользуясь интегралами площадей, получим
µx
−
+ c3 y − c2 z = l1
r
µy
(2.3.17)
−
+ c1 z − c3 x = l2 .
r
µz
−
+ c2 x − c1 y = l3
r
Таким образом, мы нашли семь первых интегралов уравнений невозмущенного движения
Умножим интегралы Лапласа (2.3.17) соответственно на c1 , c2 , c3 и сложим
−
µ
( xc1 + yc2 + zc3 ) = l1c1 + l2 c2 + l3c3 ,
r
подставим вместо c1 , c2 , c3 в левую часть их значения из (2.3.2), получим
l1c1 + l2 c2 + l3c3 = 0.
(2.3.18)
Соотношение (2.3.18) имеет простой геометрический смысл: оно выражает условие
перпендикулярности двух векторов: c (c1 , c2 , c3 ) – вектора момента количества движения и
некоторого вектора l (l1 , l2 , l3 ) , называемого вектором Лапласа. Также можно получить второе
соотношение между найденными постоянными интегрирования (c1 , c2 , c3 , l1 , l2 , l3 , h) . Возведем
каждый из интегралов площадей в квадрате и сложим:
c12 + c22 + c32 = ( yz − zy ) 2 + ( zx − xz ) 2 + ( xy − yx) 2 = y 2 z 2 − 2 yzyz + z 2 y 2 + y 2 y 2 − y 2 y 2 + z 2 x 2 − 2 xzxz + x 2 z 2 +
+ z 2 z 2 − z 2 z 2 + x 2 y 2 − 2 xyxy + y 2 x 2 + x 2 x 2 − x 2 x 2 = ( x 2 + y 2 + z 2 )( x 2 + y 2 + z 2 ) − ( xx + yy + zz ) 2 .
Отсюда получим r 2V 2 − r ′2 = c12 + c22 + c32 = c 2 , следовательно, r ′2 = r 2V 2 − c 2 (2.3.19)
2µ
+ h) − r ′2 = c12 + c22 + c32 .
(2.3.20)
r
Точно также возведем каждый из интегралов Лапласа в квадрат и сложим, в результате имеем
µ
µ
l12 + l22 + l32 = r 2 r ′2 − 2r ′2 r ′ + r ′2V 2 = r 2 ( + h) 2 + r ′2V 2 − 2r ′2 (− + V 2 ),
r
r
2µ
µ
откуда, учитывая, что h = −
+ V 2 , получим
r 2 ( + h) 2 − hr ′2 = l12 + l22 + l32 .
(2.3.21)
r
r
Исключим r ′2 из уравнений (2.3.20) и (2.3.21), окончательно найдем
(2.3.22)
l12 + l22 + l32 = µ 2 + h(c12 + c22 + c32 ) .
или
r2 (
Таким образом, из семи произвольных постоянных c1 , c2 , c3 , h, l1 , l2 , l3 независимыми являются
только пять. Поэтому семь найденных нами интегралов не образуют еще общего интеграла.
Последний недостающий интеграл может быть найден довольно легко простой
квадратурой. Действительно, из выведенных первых интегралов (2.3.2), (2.3.8) и (2.3.17) и
соотношений (2.3.18)-(2.3.22) можно выразить какие-нибудь из пяти величин x, y, z , x, y, z через
шестую (в силу независимости только пяти соотношений).
Например, выразим y, z, x, y, z через х:
y = ϕ1 ( x, h, c1 , c2 , c3 , l1 , l2 , l3 )
z = ϕ 2 ( x, h, c1 , c2 , c3 , l1 , l2 , l3 )
x = ϕ3 ( x, h, c1 , c2 , c3 , l1 , l2 , l3 )
(2.3.23)
y = ϕ4 ( x, h, c1 , c2 , c3 , l1 , l2 , l3 )
z = ϕ5 ( x, h, c1 , c2 , c3 , l1 , l2 , l3 ).
dx
Возьмем теперь одно из уравнений (2.3.23)
= x и запишем его в следующем виде:
dt
dx
= ϕ3 ( x, h, c1 , c2 , c3 , l1 , l2 , l3 ).
(2.3.24)
dt
Это соотношение представляет собой дифференциальное уравнение первого порядка с
переменными х и t. Уравнение (2.3.24) интегрируется простым разделением переменных:
dx
(2.3.25)
∫ ϕ3 ( x, h, c1 , c2 , c3 , l1 , l2 , l3 ) = t + g ,
где g – произвольная постоянная.
Из уравнений (2.3.25) принципиально возможно определить координату x как функцию
независимой переменной t. Подставляя найденное выражение для x в формулы (2.3.25) , найдем
все остальные неизвестные
x = χ1 (t , h, c1 , c2 , c3 , l1 , l2 , l3 , g ) x = χ 4 (t , h, c1 , c2 , c3 , l1 , l2 , l3 , g )
y = χ 2 (t , h, c1 , c2 , c3 , l1 , l2 , l3 , g )
y = χ 5 (t , h, c1 , c2 , c3 , l1 , l2 , l3 , g )
(2.3.26)
z = χ 3 (t , h, c1 , c2 , c3 , l1 , l2 , l3 , g ) z = χ 6 (t , h, c1 , c2 , c3 , l1 , l2 , l3 , g )
Эти уравнения представляют шесть независимых соотношений между неизвестными
функциями x, y, z, x, y, z , временем и шестью независимыми произвольными постоянными, и
составляют, следовательно, общее решение (или общий интеграл) уравнений движения.
2.4 У
Уравнения
я орбиты
c1 x + c2 y + c3 z = 0 (2.4.1)
µ r = c 2 − l1 x + l2 y + l3 z .
(2.4
4.2)
Таким обрразом, два выведенны
в
ых нами ураавнения (2..4.1) и (2.4.2) совместтно
⎪⎧c1 x + c2 y + c3 z = 0
(2.4.3)
⎨
2
⎪⎩ µ r + l1 x + l2 y + l3 z = c
определяю
ют некоторрую пространственную
ю кривую, по которой и движеттся точка P.
P Эта криввая,
очевидно, есть линия пересечеения плоскоости (2.4.1)) с поверхн
ностью (2.44.2) второгго порядка, то
есть это крривая второго порядк
ка.
Следовательно, орбита точки P в задаче двух тел есть какое-то коническое сечение, то
есть окружность, эллипс, парабола, гипербола или в вырожденном случае пара прямых.
Рассмотрим уравнение плоскости (2.4.2) более внимательно: оно показывает, что радиусвектор r текущей точки поверхности выражается рациональным образом через координаты
этой точки
1
r = (c 2 − l1 x − l2 y − l3 z ).
µ
Так как радиус-вектор r есть расстояние точки от начала координат, то отсюда следует, что
начало координат является одним из фокусов поверхности (в аналитической геометрии
фокусом поверхности или плоской кривой называется такая точка пространства, расстояние
которой от любой точки поверхности выражается рациональным образом через координаты
этой точки). Так как орбита (2.4.3) лежит на этой поверхности, а плоскость орбиты проходит
через ось вращения поверхности (2.4.2), то есть через фокусы, то орбита точки P имеет те же
фокусы и те же вершины, что и эта поверхности. Отсюда следует, что невозмущенная орбита
движущейся точки есть плоская кривая второго порядка, один из фокусов которой находится в
начале координат (то есть в центре силы притяжения), и главная или фокальная ось которой
совпадает с направлением вектора Лапласа.
Главная (фокальная) ось орбиты называется в астрономии осью апсид, точки
пересечения которой с орбитой называются апсидами. Апсиды совпадают с вершинами кривой
второго порядка и имеют каждая свое название: апсида, ближайшая к центру силы называется
перицентром, а наиболее удаленная – апоцентром (у параболы и гиперболы апоцентр не
рассматривается).
Орбитальные координаты
Поскольку орбита есть плоская кривая, то можно всегда так выбрать систему координат, чтобы
орбита лежала в координатной плоскости. И тогда все три пространственные координаты x, y, z
будут выражены в функции каких-нибудь двух независимых параметров, которые мы сейчас
выберем, и будем называть координатами точки P в плоскости орбиты или орбитальными
координатами. Рассмотрим две системы орбитальных координат: прямоугольную и систему
полярных координат.
Прямоугольная система координат Oξης : основная плоскость – плоскость орбиты Oξη ,
начало координат O – в фокусе орбиты (центре силы), положительная ось Oξ направлена к
перицентру, ось Oη ⊥ Oξ в плоскости орбиты, ось Oς ⊥ плоскости орбиты. Таким образом,
ось Oξ направлена по вектору Лапласа l (l1 , l2 , l3 ) , ось Oς – по вектору момента количества
движения c (c1 , c2 , c3 ) , ось Oη ⊥ Oξ и Oς , то есть векторному произведению вектором l и с.
Тогда направляющие косинусы новых осей через старые определяются следующим образом:
ξ
η
ς
l1 c2l3 − c3l2 c1
l
cl
c
c3l1 − c1l3 c2 . (2.4.7)
l
y 2
l
cl
c
l
c1l2 − c2l1 c3
z 3
l
cl
c
Поэтому новые координаты выражаются через старые следующим образом:
c l −c l
l
l
l
l
c ⎫
⎫
ξ = 1 x+ 2 y+ 3 z
x= 1ξ + 2 3 3 2η+ 1ς ⎪
⎪
l
l
l
l
cl
c
⎪
⎪
c3l1 − c1l3
c2l3 − c3l2
c3l1 − c1l3
c1l2 − c2l1 ⎪
l2
c2 ⎪
и
обратно
η=
x+
y+
z⎬
y= ξ+
η+ ς⎬
l
cl
c ⎪
cl
cl
cl
⎪
c
c
c
l
c ⎪
cl −c l
⎪
ς = 1 x+ 2 y+ 3 z
z = 3 ξ + 1 2 2 1η + 3 ς ⎪
⎪
c
c
c
c
cl
c ⎭
⎭
x
В новых координатах общее уравнения орбиты (2.4.3) перепишется в виде
ς =0
⎫
2
2
(2.4.10)
⎬ , где r = ξ + η .
2
µ r = c − lξ ⎭
Интегралы площадей, очевидно, примут вид:
ης − ςη = 0 , ςξ − ξς = 0 , ξη − ηξ = c .
Поскольку ς = 0 во все время движения, то первые два интеграла удовлетворяются
тождественно, и остается один, который носит название интеграла площадей в плоскости
орбиты:
ξη − ηξ = c
(2.4.11)
Введем теперь в плоскости орбиты наряду с орбитальными координатами точки P ξ и η
полярные r и v :
(2.4.12)
ξ = r cos v , η = r sin v ,
где r – радиус-вектор движущейся точки, v – угол, образуемый радиус-вектором с
положительным направлением Oξ , то есть с направлением на перицентр орбиты. Этот угол
называется в астрономии истинной аномалией и отсчитывается от перицентра против часовой
стрелки от 0 до 360 (или от 0 до ∞ ). Вследствие (2.4.12) уравнение (2.4.2) примет вид
µr = c 2 − lr cos v ,
c2
µ
Откуда r =
1+
l
µ
cosυ
. Обозначим p =
c2
µ
(2.4.14),
e=
l
µ
,
(2.4.15),
тогда уравнения орбиты приводится к хорошо известному виду коники:
r=
p
.
1 + e cos υ
(2.4.16)
2.5 Кеплеровские элементы невозмущенного движения
Вместо полученных нами ранее постоянных c1 , c2 , c3 , l1 , l2 , l3 , h, g можно ввести другие
более удобные и употребительные в астрономии постоянные, связанные с орбитальной
системой координат. Ориентация орбитальной системы координат Oξηζ относительно
системы Oxyz может быть определена, как известно, тремя эйлеровыми углами. Эти углы
имеют в астрономии свои традиционные названия.
Рассмотрим линию пересечения плоскости Oξη , то есть плоскости орбиты с плоскостью
Oxy . Эта линия называется линией узлов, а точка пересечения с орбитой N , N ′ – узлами
орбиты. Узел орбиты N, который движущаяся точка P проходит из области отрицательных
аппликат в область положительных, называется восходящим узлом Ω , а противоположный –
нисходящим. Угол Ω называется долготой восходящего узла (или просто долготой узла). Угол
между направлением на восходящий угол и направлением на перицентр ω называется
угловым расстоянием перицентра от угла. Угол между положительными направлениями
осей Oζ и Oz есть угол, под которым наклонена плоскость орбиты к основной координатной
плоскости Oxy , и называется наклонением орбиты и обозначается i . Эти три угла определяют
положение плоскости орбиты в пространстве и положение линии апсид
Долгота восходящего угла Ω отсчитывается от оси Ox в сторону движения точки P от 0
до 360 . Угловое расстояние перицентра от узла ω отсчитывается в плоскости орбиты в
сторону движения точки P от 0 до 360 . Наконец, наклонение i изменяется от 0 до 180 . При
этом, если 0 < i < 90 , то движение точки P называется прямым, а если 90 < i < 180 , то –
обратным. В большинстве случаев движение тел в Солнечной системе – прямое, в некоторых
случая – обратное.
Три введенных угла Ω , ω , i есть углы, определяющие положение одной системы отсчета
относительно другой с тем же началом координат, то есть эти три угла однозначно определяют
вращение трех координатных осей вокруг начала координат и являются известными
эйлеровыми углами. Это вращение может быть записано с помощью трех последовательных
вращений вокруг каждой из осей координат. Матрицы преобразований, описывающие правые
вращения вокруг положительны координатных осей, как известно, имеют вид:
⎧
0
0 ⎞
⎛1
⎪
⎜
A
(
)
0
cos
sin
=
θ
θ
θ ⎟⎟ − вращение на угол θ вокруг оси абсцисс
⎪ 1
⎜
⎜ 0 − sin θ cos θ ⎟
⎪
⎝
⎠
⎪
⎛ cos θ 0 − sin θ ⎞
⎪
⎪
⎜
⎟
1
0 ⎟ − вращение на угол θ вокруг оси ординат
⎨ A2 (θ ) = ⎜ 0
⎪
⎜ sin θ 0 cos θ ⎟
⎝
⎠
⎪
⎪
⎛ cos θ sin θ 0 ⎞
⎪
⎜
⎟
⎪ A3 (θ ) = ⎜ − sin θ cos θ 0 ⎟ − вращение на угол θ вокруг оси аппликат
⎜
⎪
0
1 ⎟⎠
⎝ 0
⎩
(2.5.1)
В данном случае, чтобы перейти от осей xyz к новым осям ξ ,η , ζ необходимо сделать
следующие вращения:
1) Поворот вокруг оси Oz на угол Ω (совместить ось Ox с линией узлов) - A3 (Ω) ,
2) Поворот вокруг оси Ox на угол i (поворот плоскости вокруг линии узлов) - A1 (i ) ,
3) Поворот вокруг оси Oz на угол ω (совместить ось Ox с направлением на перицентр)- A3 (ω )
Последовательность этих поворотов можно записать следующим образом:
⎛ξ ⎞
⎛ x⎞
⎛ x⎞
⎜ ⎟
⎜ ⎟
⎜ ⎟
⎜ η ⎟ = A3 (ω ) A1 (i ) A3 (Ω) ⎜ y ⎟ = A(ω , i, Ω) ⎜ y ⎟
⎜ζ ⎟
⎜z⎟
⎜z⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
(2.5.2)
на основании (2.5.1) матрица преобразования A равна
0
0 ⎞ ⎛ cos Ω sin Ω 0 ⎞
⎛ cos ω sin ω 0 ⎞ ⎛ 1
⎜
⎟⎜
⎟⎜
⎟
A = ⎜ − sin ω cos ω 0 ⎟ ⎜ 0 cos i sin i ⎟ ⎜ − sin Ω cos Ω 0 ⎟ =
⎜ 0
0
1 ⎟⎠ ⎜⎝ 0 − sin i cos i ⎟⎠ ⎜⎝ 0
0
1 ⎟⎠
⎝
⎛ cos ω sin ω cos i sin ω sin i ⎞ ⎛ cos Ω sin Ω 0 ⎞
⎜
⎟⎜
⎟
= ⎜ − sin ω cos ω cos i cos ω sin i ⎟ ⎜ − sin Ω cos Ω 0 ⎟
⎜ 0
− sin i
cos i ⎟⎠ ⎜⎝ 0
0
1 ⎟⎠
⎝
Или
cos ω sin Ω + sin ω cos Ω cos i sin ω sin i ⎞
⎛ cos ω cos Ω − sin ω sin Ω cos i
⎜
⎟
A = ⎜ − sin ω cos Ω − cos ω sin Ω cos i − sin ω sin Ω + cos ω cos Ω cos i cos ω sin i ⎟
⎜
sin i sin Ω
− sin i cos Ω
cos i ⎟⎠
⎝
(2.5.3)
Сравнивая формулы перехода от системы Oxyz к системе Oξηζ (орбитальной системы) (2.4.8)
и (2.5.2) с матрицей (2.5.3), найдем зависимости между постоянными интегрирования
c1 , c2 , c3 , l1 , l2 , l3 и эйлеровыми углами ω , Ω , i :
l1
= cos ω cos Ω − sin ω sin Ω cos i,
l
l
βτ = 2 = cos ω sin Ω + sin ω cos Ω cos i,
l
l3
γ τ = = sin ω sin i,
l
ατ =
(2.5.4)
c1
= sin i sin Ω
c
c2
= − sin i cos Ω
c
c3
= cos i
c
(2.5.5)
d ατ c2l3 − c3l2
⎫
=
= − sin ω cos Ω − cos ω sin Ω cos i ⎪
dω
cl
⎪
d
c
l
β
⎪
3 1 − c1l3
τ
′
βτ =
=
= − sin ω sin Ω + cos ω cos Ω cos i ⎬
dω
cl
⎪
d
γ
−
c
l
c
l
⎪
τ
1
2
2
1
=
= cos ω sin i
γτ′ =
⎪
dω
cl
⎭
ατ ′ =
(2.5.6)
Получим теперь выражения для координат xyz через кеплеровские элементы, заменяя в
формуле (2.4.9) направляющие косинусы их выражениями (2.5.4)-(2.5.6) через эйлеровы углы, а
орбитальные координаты их выражениями через полярные координаты (2.4.12), получим для x :
x = ξ (cos ω cos Ω − sin ω sin Ω cos i ) + ( − sin ω cos Ω − cos ω sin Ω cos i )η =
= r cos υ (cos ω cos Ω − sin ω sin Ω cos i ) + r sin υ ( − sin ω cos Ω − cos ω sin Ω cos i ) =
= r[(cos υ cos ω − sin υ sin ω ) cos Ω − (cos υ sin ω + sin υ cos ω ) sin Ω cos i ] =
cos(υ + ω )
sin(υ +ω )
= r (cos(υ + ω ) cos Ω − sin(υ + ω ) sin Ω cos i ).
υ +ω = u
x = r (cos u cos Ω − sin u sin Ω cos i )
Рассуждая аналогичным образом, мы получим выражения для двух других координат через
кеплеровские элементы. Итак,
x = r (cos u cos Ω - sin u sin Ω cos i ) ⎫
⎪
y = r (cos u sin Ω + sin u cos Ω cos i ) ⎬ ,
(2.5.7)
⎪
z = r sin u sin i
⎭
где u = υ + ω (2.5.7*) угол, образуемый радиусом-вектором r с направлением на восходящий
узел орбиты, u называется еще аргументом широты. Формулы (2.5.7) дают выражения для
прямоугольных координат точки P через истинную аномалию υ и пять постоянных: Ω, i, ω , p, e
Причем время t входит в уравнение через посредство υ .
Действительно, запишем интеграл площадей (2.4.11) ξη − ηξ = c в полярных координатах.
Поскольку
ξ = r cos v − rυ sin v ⎫
(2.5.8),
⎬
η = r sin v + rυ cos v ⎭
то (2.5.9) r 2υ = c – интеграл площадей в полярных координатах.
Уравнение (2.5.9) устанавливает связь между υ и t :
p2
dυ
= c , (2.5.10)
2
(1 + e cosυ ) dt
Это равенство легко интегрируется, обозначим через τ момент времени, когда движущаяся
точка попадает в перицентр ( υ = 0 ), тогда из (2.5.10) следует
υ
dυ
(2.5.11)
c (t − τ ) = p 2 ∫
(1 + e cos υ ) 2
0
Равенство (2.5.11) определяет t как функцию υ .
Постоянные (2.5.12) называются элементами кеплеровской орбиты или кеплеровскими
элементами невозмущенной орбиты или просто элементами орбиты.
Элементы орбиты можно разделить на две группы.
К первой группе отнесем элементы Ω, i, ω , определяющие положение плоскости орбиты
в пространстве и положение орбиты в ее плоскости.
Во вторую группу включим элементы p , e , определяющие размеры орбиты и ее форму,
и к третьей группе отнесем элемент τ , определяющий положение объекта на его орбите.
Элеементы перрвой и второй групп чисто геом
метрически
ие, связаннные с двум
мя основны
ыми
векторами
и: вектором
м момента количествва движени
ия и вектор
ром Лаплааса. При эттом элемен
нты
первой грууппы опред
деляют нап
правления этих векто
оров, а элем
менты вторрой группы
ы связаны с их
модулями
и (2.4.14), (22.4.15).
Элеемент треттьей группы
ы τ связанн с движен
нием по ор
рбите, то ессть связан с динамиккой
движения. Он называется дина
амическим
м элементо
ом.
Вы
ыражение для
д скороссти
Най
йдем теперрь выражен
ния для ком
мпонентов скорости точки
т
черезз элементы
ы орбиты. Для
Д
этого проддифференц
цируем фор
рмулы (2.55.7) по вреемени t и выразим υ и r через введенн
ные
постоянны
ые. Из (2.5.9) имеем
c
v = 2 (2.5
5.13)
r
pesin v
cessin v
p
υ=
Дифферен
нцируя вырражение (2..4.16) r =
, получим r =
.
2
p
(1 + e coss v)
1 + e cos v
Эта величина называается радиаальная скоррость
⎫
c
[e sinn υ (cos u coos Ω − sin u sin Ω cos i) + (1 + e cosυ )(− sin u coss Ω − cos u siin Ω cos i)] ⎪
p
⎪
⎪
c
y = [ e sinn υ (cos u sinn Ω + sin u cos Ω cos i ) + (1 + e cosυ )(− sin u sin Ω + cos u coos Ω cos i ) ]⎬ (2.5.15)
p
⎪
⎪
c
z = [ e sin υ sin u sin i + (1 + e cosυ ) cos u sin i]
⎪
p
⎭
x=
Если обозначить
dα
⎫
= − sin u cos Ω − coss u sin Ω cos i ⎪
du
d
⎪
dβ
⎪
β′ =
= − sin u sin Ω + coss u cos Ω coss i ⎬ (2.5.17))
du
d
⎪
dγ
⎪
= cos u sinn i
γ′=
⎪
u
du
⎭
x
⎫
= cos u cos Ω − sin u sin Ω cos i ⎪
r
⎪
y
⎪
β = = cos u sin Ω + sin u cos Ω cos i ⎬
r
⎪
z
⎪
γ = = ssin u sin i
⎪
r
⎭
α′ =
α=
Тогда общ
щее решени
ие уравнени
ий невозмуущенного движения
д
представитс
п
ся в следую
ющем виде:
x = α r, y = β r, z = γ r
⎫
c
x = [α e sin υ + α ′(1 + e cos υ )] ⎪
p
⎪
⎪
c
y = [ β e sin υ + β ′(1 + e cos υ )]⎬
p
⎪
⎪
c
z = [γ e sin υ + γ ′(1 + e co
os υ )] ⎪
p
⎭
⎫
[α e sin υ + α ′(1
1 + e cos υ )] ⎪
p
⎪
⎪
µ
⎪
[ β e sin υ + β ′(1
y=
1 + e cos υ )] ⎬
p
⎪
⎪
µ
[γ e sin υ + γ ′(1 + e cos υ )] ⎪
z=
p
⎭⎪
x=
(2.5.18)
µ
(2.5.19)
(
2.6 Осн
новные ти
ипы невозм
мущенного
о движени
ия
Первый (обобщенн
ный) закон Кеплер а. В невозмущенном
м движениии орбита движущей
йся
точки естть кривая второго порядка,
п
в одном изз фокусов которой находится центр си
илы
притяжени
ия.
Второй (ообобщенны
ый) закон Кеплера. В невозм
мущенном движении площадь, описываем
мая
радиусом--вектором движущейс
д
ся точки, иизменяется пропорцио
онально вреемени.
.
1
Действитеельно, из интеграла
и
площадей
п
((2.5.13) r 2 v = c следу
ует r 2 dv = cd
cdt , но r 2 dv = ds ессть
2
dss c
c
=
площадь ссектора с веершиной в точке О и углом dv , отсюда
(2.6. 1) или s = t + c` .
2
dtt 2
Третий заакон Кеплеера, как иззвестно, усттанавливаеет связь меж
жду средниим расстоян
нием
планеты оот центра (С
Солнца) и временем
в
еее обращен
ния вокруг центра
ц
(Соолнца). Это
от закон
имеет мессто не для всех
в
типов движения и поэтому не имеет такого общеего значени
ия, как два
первых.
Перречисленны
ые законы в поллной фор
рмулировк
ке имеют место только для
д
невозмущ
щенного дввижения, происходящ
п
щего под действием
м силы прритяжения.. Поэтомуу-то
невозмущ
щенное движ
жение часто называеттся кеплеровским дв
вижением.
Мы
ы сформули
ировали об
бщие законны, опредееляющие св
войства кееплеровского движен
ния.
Теперь раассмотрим подробнеее геометриию движени
ия. Покажеем, что тиип движени
ия полносттью
характери
изуется вели
ичиной l вектора
в
Лаппласа.
При
и е=0 траекктория движ
жения естьь окружноссть,
e<1 – элллипс,
e>1 – гиппербола,
e=1 – паррабола
l
и учитываая, что эксц
центриситет орбиты e и величин
на l связан
ны соотнош
шением (2.6
6.3) e = ,
µ
получим п
при
l =0
l<µ
l>µ
l=µ
орбита
о
естьь окружноссть
– эллипс,
– гиперболаа, (2.6.4)
– параболаа
c2
p
теряяет смысл,
µ
1 + e cos v
выроождается в прямую, а движение становится прямоугоольным.
При c = 0 из (2.44.16) следует p =
= 0 и уравн
нение (2.4.18) r =
Зависимоость типа ор
рбиты от вееличины и направлен
ния начальнной скороссти
Как мы ттолько что видели, тип орбииты характтеризуетсяя величиноой вектораа Лапласа,, а
направлен
ние этого вектора опр
ределяет пооложение орбиты
о
в еее плоскостии (линия ап
псид). Векттор
,
как
мы
ы
знаем,
ха
арактеризу
ет
положен
ние
плоско
ости
орбит
ы
в
простр
ранстве.
Та
аким
образзом
c
вектора c и l полноостью харак
ктеризуют вид и расп
положение орбиты в ппространсттве.
Оказываеттся, что тип
т
орбиты
ы можно связать и с постояянной силы
ы h , что иногда при
п
определен
нии типа оррбиты бываает предпоччтительнеее.
Для этогоо рассмотррим соотно
ошение l 2 = µ 2 + hc 2 (2
2.3.22), отк
куда учиты
ывая, что l 2 = e2 µ 2 (из
µ 2 ( e2 − 1) = hcc 2 (2.6.5)
2.6.3) полуучим
Из соотноошения (2.66.5) при c ≠ 0 следуетт:
⎧h < 0
⎪
Если ⎨h = 0 , то
⎪h > 0
⎩
а есть эллиипс
⎧e < 1, и орбита
⎪
(2.6.6)
ола
⎨e = 1, – парабо
⎪e > 1, – гипербо
ола
⎩
Постояннаая h зависи
ит от начальных значеений радиу
ус-вектора r0 и скороссти v0 (2.3.9
9):
h = V02 −
2µ
2µ
+h)
(из (2.3.8
8): V 2 =
r
r0
V0 удо
откуда слеедует, что если
е
овлетворяеет условию
ю
⎧ 2 2µ
кое
, эллиптическ
⎪V0 <
r
0
⎪
⎪ 2 2µ
, параболическ
п
кое
⎨V0 =
r0
⎪
⎪ 2 2µ
, гиперболическое
⎪V0 >
r0
⎩
(2.66.7)
В соответсствии с эти
им начальная скоростть V0 назыввается эллиптической,, параболич
ческой или
и
гиперболи
ической.
p
ринимает ви
ид r = p = cconst = r0 и из
. пр
1 + e cos υ
c2
µ 2 (e2 − 1) = hc 2 следуует, что −µ 2 = hc 2 , отткуда, учиты
ывая p = , имеем − µ = hp , и,
Отметим, что при e = 0 уравнеение r =
µ
следователльно, поскоольку V02 = h +
µ
2µ
(2.6.9) естть круговаяя начальнаяя скорость.
, тто V0 =
r0
r0
Итак, тип орбиты заависит от величины
в
нначальной скорости и начальноого радиус-вектора. Так
Т
как скороссть всегда направлена
н
а по касатеельной к тр
раектории, то вектор сскорости вссегда лежи
ит в
плоскости
и орбиты, так же каак и векторр положен
ния r0 . Таким образзом вся гео
ометрическкая
картина ддвижения в простраанстве хараактеризуеттся двумя векторамии: векторо
ом начальн
ной
скорости V0 ( x0 , y0 , z0 ) и векторо
ом положенния в начал
льный мом
мент r0 ( x0 , y 0 , z0 ) .
Зави
исимость типа
т
орби
иты от велличины и направл
ления начаальной ск
корости
2.7 Элли
иптическоее движениее. Уравнени
ие Кеплераа
v
dv
∫ (1 + e cos v)
0
2
=
µ
c
(t − τ ) = 3/2 (2
2.7.1)
2
p
p
Однако, ээтот прямоой путь реешения окказывается трудно вы
ыполнимым
м. Поэтом
му избираеттся
другой п
путь: поссредством введенияя некотор
рой вспо
омогательноой перем
менной. Эта
Э
вспомогаттельная переменная вводитсяя различн
ными способами ддля эллиптического и
гиперболи
ического движения,
д
поэтому ккаждый изз этих слу
учаев прииходится рассматрива
р
ать
отдельно. Для элли
иптическогго случая вспомогаттельная переменная вводится следующ
щим
образом:
v
1+ e E
tg =
tg
(2.7.2),
2
1− e 2
Продиффееренцируем
м (2.7.2) по
о времени:
sec2
v
1+ e
E
dvv =
seec2 dE (*)
2
2
1− e
Посколькуу
v
v
1+ e 2 E
tg
=
sec2 = 1 + tg 2 = 1 +
1− e
2
2
2
1 − e + (1 + e)tg 2
1− e
E
E
E ⎤
⎡
⎛
⎞
e(cos 2 − sin 2 ) ⎥
⎜
⎟
⎢
1
1
1
1
−
e
cos
E
2 =
2
2 =
−
⎜
⎟
⎥
⎢
−
1 − e ⎢ cos 2 E
1
e
2 E
2 E
⎜
⎟
⎥
cos
ccos
⎦
⎝
2 ⎠
2
⎣
2
1 − e2
dE (2
то из (*) dv =
2.7.4).
1 − e cos E
v 1 − e cos E 2 E
sec
следователльно sec =
( 2.7.3),
2
2
1− e
2
+ cos v = 2 co
os 2
Далее, посскольку 1+
(имея в ви
иду, что secc 2
v
2
=
(2.7.3)
2 sec 2 v
2
E
2
=
), откууда
2 1 + co
os E
1 + e cos
c v = 1+
cos v =
имееем 1 + cos v =
1− e
(1 + cos E ) ,
1 − e cos E
cos E − e
(2.7.5)
1 − e cos E
e (cos E − e)
1 − e2
=
(2.7.6)
1 − e cos E 1 − e cos E
µ
dv
1 − e cos E
∫0 (1 + e cos v)2 = ∫0 (1 − e2 )3/2 ddE = a3/2 (1 − e2 )3/2 илли,
v
Подставляяя (2.7.6) и (2.7.4) в (2
2.7.1), полуучим
E
посколькуу p = a(1 − e2 ) ,
E
∫ (1 − e cos E )dE = a
µ
3/2
(t − τ )
(2.77.7)
0
Выражени
ие (2.7.7) леегко интегр
рируется,
E − e s in E =
Положим n =
µ
a
3/ 2
µ
a
3/ 2
(t − τ )
(2.77.8)
(22.7.9) и M = n (t − τ ) (22.7.9’), тогд
да уравнен
ние (2.7.8) пперепишетсся в виде
E − e sin E = M (2.7.10)
цендентное уравнени
ие определяяет вспомогательную переменнуую E и наззывается
Это трансц
уравнени
ием Кеплер
ра. Его реш
шение найтии несложно
о, например, методом
м последоваательных
приближении, если известны
и
e и M:
Полагаем E0 ∼ M
⎧ E1 = e sin E0 + M
⎪ E = e sin E + M
⎪
1
E = e sin E + M :→ ⎨ 2
⎪.............................
⎪⎩ En = e sin En −1 + M
м
велиичина.
пока | En − En−1 |< ε – заданная малая
Решение уравненияя (2.7.10) можно наайти такж
же разложеением, наппример, в ряд Фуррье:
Фурье как нечетная тригонометриическая фу
ункция.
E − M = e sin E , e sin E разлагаеттся в ряд Ф
Выясним смысл вв
веденных величин
в
E, M .
Легко показать, что ∠ПСР′ = E . В то время, как радиус-вектор точки Pописывает угол v ,
радиус-вектор проекции точки P на окружность радиуса a (большая полуось с центром в
центре эллипса описывает угол E ).
Угол E называется эксцентрической аномалией.
Очевидно, чтобы доказать, что ∠ПСР′ = E , надо показать, что для E = ∠ПСР′ справедливо
(2.7.2)
tg
v
1+ e E
tg .
=
2
1− e 2
CO CO
=
, CO = ae
CП
a
следовательно CN + NO = ae , но CN = a cos E , NO = −r cos v откуда a cos E − r cos v или
a(1 − e2 )
a
1 − e2
cos v ,
cos v = cos E − e (2.7.10’) подставляя сюда r =
, получим cos E − e =
1 + cos v
r
1 + e cos v
cos E − e
cos E − e + e cos E cos v − e2 cos v = cos v − e2 cos v , и следовательно, cos v =
, но это
1 − e cos E
выражение совпадает с (2.7.5), полученным из (2.7.2). Точно также можно показать, что
совпадают и выражения для sin v . Действительно из (2.7.2) следует, что, поскольку
Доказательство: CN + NO = CD , по определению эксцентриситета e =
tg
v
sin v
=
,
2 1 + cos v
то
sin v
1 + e sin E
=
,
1 + cos v
1 − e 1 + cos E
подставляя
сюда
(2.7.5),
получим
1 − e2
sin v =
sin E (2.7.11).
1 − e cos E
v
v
2sin cos
v
2
2 = sin v ,1 + cos v = cos E − e + 1 = (1 − e)(1 + cos E ) (*)
tg =
v
2
1 + cos v
1 − e cos E
1 − e cos E
2 cos 2
2
Это же выражение получим и из рисунка 1:
PN b
P′N = a sin E , PN = r sin v,
= = 1 − e2 и следовательно r sin v = 1 − e2 a sin E
(2.7.12),
P′N a
a(1 − e2 )
a(1 − e 2 )
sin v = a 1 − e2 sin E , подставим сюда
подставляя сюда r =
, получим
1 + e cos v
1 + e cos v
1 − e2
(2.7.6)
1 − e cos E
полностью совпадает с (2.7.11)
выражение 1 + e cos v =
для 1 + e cos v , получим sin v =
1 − e2
sin E , что
1 − e cos E
Выясним теперь смысл величины n.
Пусть движение начинается из перицентра (v = 0) . Обозначим через T время полного оборота
точки вокруг центра силы. Тогда уравнение Кеплера (2.7.10) дает с учетом M = n (t − τ ) (2.7.9’)
2π
(2.7.13).
T
Следовательно n есть средняя угловая скорость движущейся точки и называется в астрономии
средним движением точки. Формула (2.7.9) показывает, что среднее движение n связано с
v = E = 2 π, E − e sin E = nT = 2π , откуда n =
большой полуосью орбиты соотношением n2 a3 = µ (2.7.14).
Вы
ыясним теп
перь смысл величин
ны M .
Формула ((2.7.9’) покказывает, что M возррастает про
опорционал
льно временни, обращааясь в 0,
когда точкка P находи
ится в пери
ицентре, таккже как v и E , и M = 180 0 в аппоцентре (и
из уравнени
ия
Кеплера: E − e sin E = M , при E = M = 18000 ). Если мы
м представим теперьь фиктивну
ую точку,
движущую
юся по окруужности раадиуса a с постоянной угловой скоростью
с
n , то M будем
б
равнаа
углу, котоорый образуует радиус-вектор этоой фиктивн
ной точки с направленнием на перицентр.
Отметим ттеперь, чтоо для эллип
птического движения имеет местто третий ззакон Кеп
плера.
то есть спрраведливо
T12 m0 + m1 a13
= (2.7..16).
T22 m0 + m2 a23