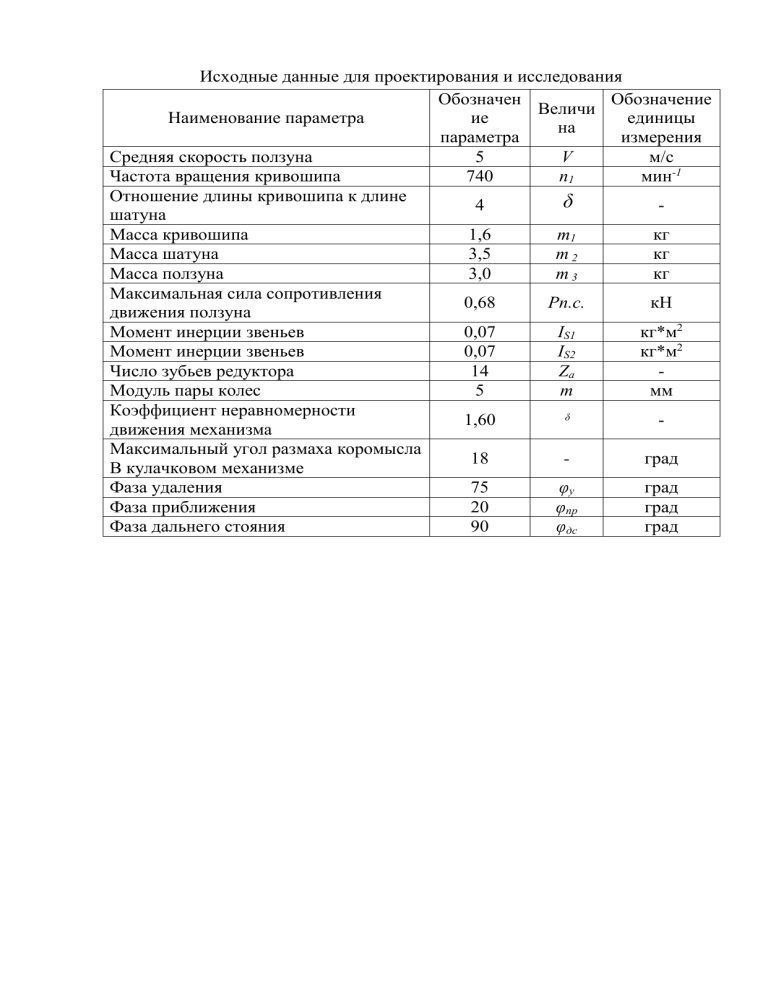
Исходные данные для проектирования и исследования Обозначен Обозначение Величи Наименование параметра ие единицы на параметра измерения Средняя скорость ползуна 5 V м/с Частота вращения кривошипа 740 n1 мин-1 Отношение длины кривошипа к длине 4 шатуна Масса кривошипа 1,6 m1 кг Масса шатуна 3,5 m2 кг Масса ползуна 3,0 m3 кг Максимальная сила сопротивления 0,68 Рп.с. кН движения ползуна Момент инерции звеньев 0,07 IS1 кг*м2 Момент инерции звеньев 0,07 IS2 кг*м2 Число зубьев редуктора 14 Za Модуль пары колес 5 m мм Коэффициент неравномерности 1,60 ᵟ движения механизма Максимальный угол размаха коромысла 18 град В кулачковом механизме Фаза удаления 75 φу град Фаза приближения 20 φпр град Фаза дальнего стояния 90 φдс град ᵟ 1. РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1 Синтез, структурное и кинематическое исследование механизма 1.1. Структурное исследование рычажного механизма Кривошипно-ползунный механизм состоит из четырех звеньев: 0 – стойка, 1 – кривошип, 2 – шатун, 3 – ползун. Также имеются четыре кинематические пары: I – стойка 0-кривошип OA; II – кривошип OA-шатун AB; III – шатун AB-ползун B; IV – ползун B-стойка 0. I, II и III являются вращательными парами; IV – поступательная пара. Все кинематические пары являются низшими, т.е. pнп=4, pвп=0. Степень подвижности механизма определяется по формуле П.Л. Чебышева: W=3*n-2pнп-pвп, (1) где n – число подвижных звеньев, n =3 Pнп – число низших пар, Pвп – число высших пар. W=3*3-2*4=1. По классификации И.И. Артоболевского данный механизм состоит из механизма I класса (стойка 0-кривошип OA) и структурной группы II класса второго порядка (шатун AB-ползун B). Из этого следует, что механизм является механизмом II класса. 1.2 Проектирование кривошипно-ползунного механизма Длину кривошипа l1 определяем из рассмотрения двух крайних положений механизма, определяющих ход ползуна S. Длина кривошипа равна половине хода ползуна, т.е.: lOA15·V/n1 (2) lOA0,10 м. Длина шатуна определяется через заданное отношение : lABlOA· (3) lAB0,40 м Расстояние от точки А до центра масс S2 шатуна AS20,35lAB (3) AS20,10 м 1.3. Построение схемы механизма План положений - это графическое изображение механизма в n последовательных положениях в пределах одного цикла. План положений строим в двенадцати положениях, равностоящих по углу поворота кривошипа. Причем все положения нумеруем в направлении вращения кривошипа 1 . Положения остальных звеньев находим путем засечек. За нулевое начальное положение принимаем крайнее положение, при котором ползун наиболее удален от кривошипного вала начало работы хода. Начальное положение кривошипа задается углом 0, отсчитанным от положительного направления горизонтальной оси кривошипного вала против часовой стрелки. Для данного 02,356 механизма 2 последовательно соединяющая центры S 0 , S 1 2 2 , S 2 …S 12 2 рад. Кривая, масс шатуна в различных его положениях, будет траекторией точки S2. Выбираем масштабный коэффициент длин l: l lOAOA (4) где l1-действительная длина кривошипа, м. OA-изображающий её отрезок на плане положений, мм. l0,10500,002 ммм. Отрезок AB, изображающий длину шатуна l2 на плане положений, будет: ABlABl AB0,400,002=200 мм. (5) 1.4. Построение планов скоростей Построение начинаем от входного звена, т. е. кривошипа ОА. Из точки Рv, принятой за полюс плана скоростей, откладываем в направлении вращения кривошипа ОА вектор скорости точки А: Pv = 50мм. Определим скорость точки А V A 1 LOA 740 3,14 * 0.10 7,85 м / с 30 (7) Определим масштаб плана скоростей: v vA 7,85 м/c 0.157 Pv a 50 мм (8) где: (Pva) – отрезок отображающий на плане скоростей скорость точки А, и равный 50 мм. Произведём все вычисления для второго положения механизма, определим скорость точки В из векторного уравнения: v B v A v BA где: v A –вектор скорости точки А направлена OA; v BA –вектор скорости точки B относительно A, и направлена BA; v B –вектор скорости т.B; vb v Pvb 19,4 * 0.157 3,05 м / с (9) v BА v ba 43,66 * 0.157 6,85 м / с Скорость точки S2 находим из условия подобия: as2abAS2AB, (10) as2AS2ABab, (11) VS2Ps2V, (12) VS240,150,1576,3 мс. Если из произвольной точки отложить вектор VS2 для всех двенадцати положений и соединить их конечные точки плавной кривой, то получим годограф скорости точки S2. Угловую скорость шатуна AB определяем по формуле: 2VBAlAB, (13) 26,580,4116,91 . -1 Таблица 1. Параметр Номер положения механизма 4 5 6 7 8 9 1 2 3 10 11 12 vВ 3,05 5,90 7,85 7,69 4,80 0,00 4,80 7,69 7,85 5,90 3,05 0,00 v BA 6,85 4,03 0,00 4,03 6,85 7,85 6,85 4,03 0,00 4,03 6,85 7,85 vS 2 6,30 7,20 7,85 7,61 6,57 5,89 6,57 7,61 7,85 7,20 6,30 5,89 2 16,91 9,93 0,00 9,93 16,91 19,36 16,91 9,93 0,00 9,93 16,91 19,36 1.5. Построение планов ускорений Построение плана ускорений произведём для 5, 6 и 11 положения механизма. Т.к. кривошип О1А вращается с постоянной круговой скоростью, то точка А имеет только нормальное ускорение: a A a An 12 LOA ( 740 3,14 2 ) * 0.10 608,00 м / с 2 30 а 608,01 / 50 12,16 м / с2 мм (14) (15) Определим ускорение т. В решив систему векторных уравнений: n a B a A a BA a BA где: a B – вектор ускорения т.B; aA – вектор ускорения т.A, определили по правилу подобия; n a BA –вектор нормального ускорения точки B относительно точки A, направлен от т. B к т.A; a BA –вектор тангенциального ускорения точки B относительно точки A, направлен BA; 1.5.1. Нахождение ускорений и их масштабных отрезков Для 5, 6, 11 положений механизма найдём величины следующих ускорений: a n BA 2 V BА 6,85 2 / 0,40 115,74 м / с 2 L BA n a BA n a BA (16) 2 V BА 7,85 2 / 0,40 152,00 м / с 2 L BA 2 V BА 6,85 2 / 0,40 115,74 м / с 2 L BA Их масштабные отрезки равны: n nBA a BA 115,74 9,51мм а 12,16 n nBA a BA n nBA a BA (17) 152,00 12,5 мм а 12,16 115,74 9,51мм а 12,16 Рассчитав нормальные ускорения и их масштабные отрезки, результаты сведём в таблицу 2: Таблица ускорений и их масштабных отрезков. Таблица 2. n а BА n BA Един. из. 5 положение 6 положение 11 положение м / с2 мм 115,74 152,00 115,742 9,52 12,50 9,518 1.5.2. Численные значения ускорений, а также касательных ускорений найдём, перемножив соответствующий отрезок плана ускорений на масштаб плана ускорений, и данные занесём в таблицу 3. а в а P aв 49,73 *12,16 604,73 м / с 2 (18) а BА а n1 c 23,99 *12,16 291,72 м / с 2 а S 1 а P aS 1 304,00 м / с 2 а S 2 а P aS 2 48,58 *12,16 590,74 м / с 2 а S 3 а P aS 3 49,73 *12,16 604,73 м / с 2 2 а BА 291,72 719,58 рад / с 2 о L BА 0,40 (19) Таблица 3. Ускорение 5 положение 6 положение 11 положение aВ 604,73 763,66 448,22 a BA 291,72 0,00 291,72 a S1 304,00 304,00 304,00 aS 2 590,74 646,92 555,36 aS 3 604,73 763,66 448,22 2 719,58 0,00 719,58 1.5.3 Построение кинематической диаграммы точки B Метод диаграмм позволяет определить кинематические характеристики движения одной точки. Для построения диаграммы перемещения точки B, откладываем по оси абсцисс отрезок 0-0 равный 240 мм, изображающий период Т оборота кривошипа, и делим его на 12 равных частей. Рассчитаем масштабы необходимые для построения графиков: М s l 0.002 ММ 60 60 0,08 n 740 T T 0,08 t 0.00034 c м м O O lg 240 T (20) (21) По оси координат откладываем соответствующие отрезки О0-О1, О0-О2 и т.д. Полученные точки соединяем плавной кривой. Диаграмму скорости получаем дифференцируя график перемещения точки В методом хорд, а график ускорения точки получаем дифференцируя кривую скорости, также методом хорд. Определим масштабы: v a s t H v t H 0.0020 0.15 ммм/ с 40 * 0.00034 0.15 / с2 11,1 ммм 40 * 0.00034 где: Н1 и Н2 – полюсные расстояния графиков соответственно равные 40 мм. Значения скорости и ускорения точки В занесём в таблицу 4, также рассчитав при этом процент ошибки при определении скорости т. В, используя следующую формулу: vвек vграф v 100 % vграф Таблица 4 Параметр 1 2 3 4 Положение механизма 5 6 7 8 9 10 11 12,0 v В ,м/с 3,08 5,73 7,64 7,57 4,78 0,00 4,78 7,57 7,64 5,73 3,08 0,00 ПС. v В ,м/с 3,05 5,90 7,85 7,69 4,80 0,00 4,80 7,69 7,85 5,90 3,05 0,00 v ,% 1,14 2,97 2,72 1,64 0,40 0,00 0,40 1,64 2,72 2,97 -1,14 0,00 623,71 734,04 426,13 604,73 763,66 448,22 -3,04 4,03 5,19 a В ,м/с2 ПС a В ,м/с а , % 2 Вывод: Проанализировав полученные результаты можно сделать следующий вывод: в целом результаты расчёта можно считать удовлетворительными, на процент ошибки, при расчёте скорости точки В, оказал влияние недостаточно точный метод дифференцирования графика перемещения т. В РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 2 РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 3 3.2. Профилирование зубчатых колес. Частота вращения эл.двигателя nдв.: 1400 об/мин. Частота вращения кривошипа nкр: 540 об/мин. Передаточное отношение: u12=nдв/nкр= 2,6. Параметры зуборезной рейки: z1=22; z2=57; m=6. Радиус начальной окружности первого колеса: 66 Радиус начальной окружности второго колеса: 171 Межосевое росстояние: 237 Радиус основной окружности первого колеса: 62,0197131062811 Радиус начальной окружности второго колеса: 160,687438502637 Величины радиусов впадин Нормального зуба при х'' = 1,1: 59,4 Укороченного зуба при x'' = 1,1: 164,4 Галтель радиуса: 1,5 Шаг по делительной окружности: 18,8495556 Толщина зуба по делительной окружности: 9,4247778 Величины радиусов вершин Нормального зуба при x'' = 1,0: 72 Укороченного зуба при x'' = 1,0: 177 Передаточное отношение от первого зубчатого колеса ко второму: 2,59090909090909 Передаточное отношение от второго зубчатого колеса к первому: 0,385964912280702 Коэффициент перекрытия при x'' = 1,0: 1,67864118578649 Удельное скольжение первого колеса при x'' = 1,0: 0,216731783262325 второго колеса при x'' = 1,0: -0,276701873803862 Отношение удельного скольжения первого колеса ко второму при x'' = 1,0: 0,783268216737676 Действительная толщина зуба по дуге головок для первого колеса при x'' = 1,0: 4,2361230566295 для второго колеса при x'' = 1,0: 4,69762245557163 Толщина зуба по дуге головки: нормального зуба первого колеса при x'' = 1,0: 2,3534016981275 нормального зуба второго колеса при x'' = 1,0: 2,60979025309535 Отрезок (АВ)-теоретическая линия зацепления которая показывает начало и конец работы пары зубьев. В принятом масштабе откладываем межосевое расстояние А0. Из центра О1 проводим дугу радиусом R g ; из О21 Rg 2 Через полюс Р0 проводим к дуге основной окружности касательную (N- N) под углом 0=20 к (Т-Т). Проводим дуги радиусов r01 и r02. Построение эвольвенты. Отрезки Р0А и Р0В делим на равное число отрезков и получаем точки 1,2,3 … и т.д. Точки 1,2,3… и т.д. переносим на дуги основных окружностей, получим точки 1,2,3… и т.д. К точкам 1,2,3… и т.д. проводим касательные. На касательных от точек 1,2,3… и т.д. откладываем отрезки. Соединяя засечки на касательной плавной кривой получим эвольвенту бокового профиля зуба. Сверху эвольвента ограничивается радиусом головок. Rr Rg h , 1 где h-высота головки зуба. Высоту головки зуба можно определить по формуле: h f m , Для построения симметричного бокового профиля необходимо от полюса А по дуге делительной окружности отложить шаг зацепления, t: t m мм Толщину зуба S T , и толщину межзубового пространства можно 3 определить по формуле: 1 ST3 S M 3 t 2 Так как по делительной окружности толщина зуба S T равна толщине 3 межзубового пространства S M .Определяем рабочие участки зуба перенеся 3 точки a и b на сопряженные профили. РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 4 4. Синтез кулачкового механизма 4.1 Параболический закон φ1= 120 ˚ 2,0933 рад. Lд= 240 (мм) φ2= 30 ˚ 0,5233 рад. S= 0,0376 (м) φ3= 80 ˚ 1,3956 рад. h= 60 (мм) Строим оси координат S=S(φ). По оси абсцисс откладываем фазовые углы φy, φдсφп в масштабе µl=: µl=Ʃφ/Lд= 0,0164 рад/мм φ1= 96 (мм) φ2= 16 (мм) φ3= 128 (мм) Углы jy и jп делим на 8 равных частей. Получим точки 0,1,2... 17. Че­рез эти точки проводим перпендикуляры к оси абсцисс. На перпенди­куляра 8 и 9 откладываем ход толкателя 8 в масштабе µs : µS= 0,00065 м/мм График перемещения строится в координатах S=f(φ) (см. рисунок 4). По оси ординат откладывают отрезок h=30...60 мм, соответствующий ходу толкателя S, и тогда масштаб диаграммы перемещений определяем по формуле (5). По оси абсцисс в принятом масштабе откладывают фазовые углы φ 1, φ2 и φ3. Отрезки, соответствующие φ1 и φ3, делят на 8 равных частей. Точки нумеруют, как показано на рис. 4. В точке 4 проводят ординату, равную h, которую тоже делят на 8 равных частей. Точки деления обозначают цифрами 1, 2, 3,...8. Точки 1, 2, 3 соединяют прямыми с началом координат, а точки 5, 6, 7 - с точкой 8*. Точки пересечения прямых (0 – 1), (0 – 2), (0 – 3), (8* – 5), (8* – 6), (8* – 7) с ординатами 1, 2, 3,...8 являются искомыми точками параболы. Аналогично проводят построения для фазы возвращения. Для построения графика dS f ( ) определяют ординаты (4 - 4') для d фазы удаления и (13 -13') и для построения графика d 2S вычисляют ординаты d 2 по формулам: (4 4 / ) 2h 1 (13 13/ ) (4 4 ) // , 2h 3 4h 12 (13 13 // ) . 32 57,3248 (мм) (13-13)= 85,9873 (мм) (4-4")= 54,769 (мм) (13-13")= , 4h (4-4')= 123,23 (мм) . 4.2. Определение минимального радиуса кулачка Коромысловый толкатель с роликом. Для кулачкового механизма с коромысловым толкателем определяют радиус основной шайбы кулачка, а также межцентровое расстояние А. Исходными данными при проектировании являются фазовые углы, длина коромысла l и угол качания коромысла DY. Между ходом толкателя, длиной коромысла и углом качания имеется следующая взаимосвязь: Минимальный радиус кулачка определяем графическим способом. Для этого из произвольной точки О4проводим дугу радиусом, равным длине коромысла О4С0 в масштабе μе. От начального положения коромысла О4С0 откладываем угол качения βmax. Путь центра ролика C0C6 размечаем в соответствии с диаграммой β = β(φ). Через полученные точки C1, C2, C3, C4, C5 проводим лучи O4C1, O4C2………O4C5, представляющие собой как бы мгновенные положения коромысла при его перемещении в соответствии с заданным законом движения. На лучах от точек C1…….C5 откладываем отрезки Zi, изображающие соответствующие значения величины в масштабе µe.. Направление вращения кулачка принимаем противоположным направлению вращения коромысла при его удалении. Поэтому отрезки Z откладываем на промежуточных положениях коромысла вправо от дуги C0C6 при удалении коромысла и влево при возвращении его. Соединив последовательно конечные точки отрезка Z0, Z1, Z2,…….плавной кривой, получаем геометрическое место концов отрезков Z = Z(S). К полученной диаграмме проводим касательные под углом 45° Точка пересечения этих касательных 01. Касательные ограничивают область существования радиуса кулачка. Выбираем точку 0 . Отрезок 01- 0 минимальный радиус кулачка. rmin Rmin s ds d м 4.3 Построение профиля кулачка. Для построения профиля кулачка графическим путем используем метод обращения движения (метод инверсии). Он заключается в том, что всему кулачковому механизму сообщается движение вокруг оси кулачка с угловой скоростью, равной угловой скорости ведущего звена, но противоположно ей по направлению. В результате кулачок останавливается, коромысло получает вращение с угловой скоростью ω1, а ведомое звено совершает плоское движение. При этом относительное движение звеньев кулачкового механизма сохраняется неизменным. Для построения профиля кулачка графическим способом используем метод обращения движения (метод инверсии). Строим треугольник O2O4C0 со масштабе µe. Радиусом равным O4C0 проводим дугу, стягивающую угол βmax. Эту дугу делим на части, пропорциональные ординатам графика S = S(φ). В сторону противоположную вращению кулачка от O2O4 откладываем углы φу, φg, φв. Дуги стягивающие углы φу и φв делим на 6 равных частей. Из точек деления этих дуг радиусом, равным длине коромысла делаем засечки на соответствующих дугах, проведенных из центра О2 через точки деления дуги С0С6. Соединив плавной кривой засечки, получаем центровой профиль кулачка. Практический профиль вычерчиваем как огибающую семейства дуг радиуса, равного радиусу ролика, которые проведены из центров, расположенных на центровом профиле кулачка.