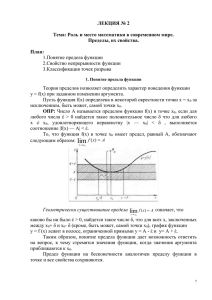
10 класс Предел функции Предел функции в точке Предел функции при х а существует когда существуют и равны между собой оба односторонних предела. lim f ( x) 2 левый предел x 3 0 lim f ( x) 2 правый предел x 3 0 2 lim f ( x) 2 предел существует x 3 3 Предел функции в точке 4 2 2 2 3 3 3 Предел функции в точке 4 2 2 2 3 3 lim f ( x) 2 lim f ( x) 2 2 f (3) 2 f (3) f (3) не сущ. f (3) 4 x 3 x 3 3 lim f ( x) 2 f (3) x 3 Предел функции Предел функции в точке Определение. Число А называется пределом функции f ( x) в точке х а, если для любого 0 существует такое число 0 , что для всех х, удовлетворяющих условию 0 x a выполняется неравенство f ( x) A . А а Примеры Примеры Предел функции в точке Предел функции в точке Предел функции в точке