
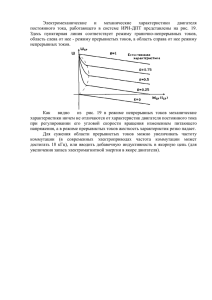
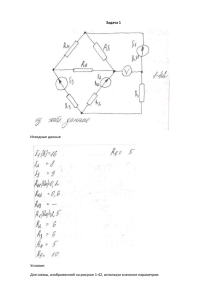
Применение метода симметричных составляющих для расчета несимметричных режимов. I. Схема замещения электроэнергетической системы для токов прямой последовательности. Это симметричный режим, поэтому его можно представить схемой замещения для одной фазы. Она абсолютно такая же, как и для расчета трехфазных КЗ, единственное отличие – в точке КЗ включается напряжение прямой последовательности особой фазы, например, фазы А UkA1 (k – место данного параметра, т.е. точка КЗ, A – фаза на которую рассматривается данный параметр, 1 – прямая последовательность) E3 X6 E1 K1 X4 X3 X1 X2 X7 E 4 X5 UkA1 I kA1 X8 E2 E5 Сопротивления всех элементов схемы замещения и ЭДС генераторов и нагрузок определяются также, как для симметричного КЗ. В результате преобразования схем замещения получим: E1Σ jX1Σ K1 U kA1 Ι kA1 Где x1Σ, E1Σ – результирующее сопротивление и ЭДС схемы замещения прямой последовательности Считаем, что токи направлены всегда к точке КЗ, даже если по логике они должны быть направлены в обратную сторону. В этом случае значения токов будет отрицательным. Из этой схемы замещения: U&kA1 = E&1 jx1 I& kA1 (2) II. Схема замещения электроэнергетической системы для токов обратной последовательности. Особенности: Сопротивления элементов схемы замещения для токов обратной последовательности, соответствующие оборудованию, не имеющих вращающегося магнитного поля равны их значениям для токов прямой последовательности и симметричных токов. Элементы оборудования, содержащие вращающееся магнитное поле, имеют сопротивление для токов обратной последовательности отличающееся от сопротивлений для токов прямой последовательности. ЭДС генератора будет равно нулю, т.к. на шинах генератора при правильном соединении обмоток статора (порядок чередования фаз) имеет место лишь ЭДС прямой последовательности Тоже самое касается ЭДС обобщенной электрической нагрузки, т.к. основную их долю составляют асинхронные двигатели. Значок ˅ указывет на то, что сопротивление элемента изменится относительно схемы прямой последовательности. ˅ X6 ˅ X1 X3 K2 X4 X7 UkA 2 ˅ X2 ˅ X5 I kA 2 ˅ X8 Величины сопротивления обратной последовательности обобщенной нагрузки в относительных единицах следующие: xН *2 = 0,35 (35кВ и ) xН *2 = 0,45 (6 10 кВ ) Преобразование схемы замещения к простейшему виду относительно точки КЗ: K2 jX2Σ UkA 2 Ι kA 2 Где x2 – результирующее сопротивление схемы замещения обратной последовательности. Из этой схемы замещения: U&kA2 = 0 jx2 I& kA 2 (2) III. Схема замещения электроэнергетической системы для токов нулевой последовательности. В данной схеме действуют напряжения и протекают токи нулевой последовательности. Основная особенность токов и напряжений нулевой последовательности состоит в том, что во всех трех фазах в ветви КЗ они равны по величине и по фазе. Эта особенность при водит к серьезным отличиям в формировании самой схемы замещения для токов нулевой последовательности, а также в определении сопротивлений линий для токов нулевой последовательности. Рассмотрим причины этих особенностей. Пусть имеем K(1) Рассмотрим протекание токов для прямой и нулевой последовательности. Для этого рассмотрим, как выглядит схема замещения прямой последовательности этого участка сети в трехфазном исполнении: а а c А I kA1 В I kB1 С I kC1 K1 UkB1 UkA1 b UkC1 I Поскольку симметричные составляющие напряжений прямой последовательности равны друг другу только по величине, но не по направлению, то в каждой фазе будет действовать свое напряжение, смещенное относительно любого другого на 120 градусов. При этом, запись первого закона Кирхгофа в точке (а) будет следующей: & & & I& kA1 I kB1 I kC1 I Исходя из наличия симметричной системы токов в сети токи, находящиеся в левой части уравнения, обратятся в ноль, т.е. скомпенсируют сами себя: I kB1 I kA1 I kC1 I kB1 I kA1 I kC1 В результате получим, что при растекании токов прямой последовательности токи через землю не протекают: 0 I& Аналогичная ситуация наблюдается при рассмотрении обратной последовательности, единственным отличием будет обратное чередование фаз в векторной диаграмме токов. В трехфазном исполнении схема замещения для токов нулевой последовательности будет иметь следующий вид: c I0 А а В I0 С I0 b 3 I0 3 I0 K0 UkA0 UkB 0 UkC 0 Исходя из рисунка в контуре протекания токов нулевой последовательности появляется земля, т.к. в данном случае токи по всем фазам равны по величине и аргументу. Выражение для этого тока появляется при записи первого закона Кирхгофа для той же точки (а): I0 I0 I0 I I = 3I0 Отличительной особенностью является сложность учета контура протекания тока нулевой последовательности, т.к. в этот контур попадает земля и необходимо смоделировать распространение токов в земле и, соответственно, получить выражение для сопротивлений линий для токов нулевой последовательности (для одной фазы). Для получения выражений для всех вариантов трехфазной ЛЭП начнем от простейшего случая однопроводной линии и закончим двухцепной трехфазной линией. 1. Однопроводная линия «провод-земля» переменного тока I0 U0 Покажем распределение тока для однопроводной линии при возврате тока через землю. r D j распределение плотности тока обратный провод Исходя из рисунка распределения плотности тока по поверхнсти земли и вглубь, для моделирования предложена к использованию величина, называемая эквивалентной глубиной возврата тока через землю. D 20.85 м 1000 м , f Где f [Гц] – частота; λ [1/(Ом∙см)] – удельная проводимость земли. Индуктивное сопротивление "провод-земля" можно определить по формуле для двухпроводной линии: x01 0.145lg D Ом км rпр Если имеем дело с расщепленным проводом (т.е. в каждой фазе ЛЭП подвешено больше 1 провода), то необходимо найти эквивалентный радиус провода, с учетом расщепления: Rэкв n rпрd1 d 2 ... d n 1 , Где n – число проводов в фазе; α = 0,8 ÷ 0,9 – коэффициент учитывает реальное сечение, по которому протекает ток; di – расстояние от любого провода в фазе до остальных проводов; rпр – радиус одного провода. Активное сопротивление земли: rз 2f 104 0.05 Ом при f 50 Гц км Далее будем проводить рассмотрение без учета активных составляющих сопротивлений. x01 0.145lg D Ом (1) км Rэкв λ [1/(Ом∙см)] – удельная проводимость земли. 2. Двухпроводная линия переменного тока d I0 I0 U0 x0дв x01 x012 x012 0.145lg D Ом км d Тогда x0дв 0.145lg D D D2 D Ом 0.145lg 0.145lg 0,29lg км Rэкв d Rэквd Rэквd Rэквd Rср , Где Rср – средний геометрический радиус двухпроводной системы. x0дв 0.29lg D Ом (2) км Rср 3. Трехфазная линия переменного тока d12 1 I0 2 d 23 d13 I0 3 I0 U0 x 01 0.435lg D Ом км 3 R d d экв 12 13 x 02 0.435lg D Ом км 3 R d d экв 12 23 x 03 0.435lg D Ом км 3 R d d экв 13 23 На трехфазных линиях применяют транспозицию для того, чтобы индуктивное сопротивление каждой фазы было одинаковое: А В С С учетом транспозиции проводов результирующее сопротивление для токов нулевой последовательности будет равно среднему значению из трех полученных (считая на одну фазу): X0I – удельное индуктивное сопротивление одной фазы трехфазной ЛЭП для токов нулевой последовательности x0 I 1 1 D D x x x 0.435lg 01 02 03 0.435lg 3 3 R d d 3 3 Rэквd12d13 экв 23 12 0.435lg D 3 R d d экв 13 23 D Ом 0.435lg 2 км Rэкв 3 d12d 23d13 Rэкв 3 d12d23d13 RсрI 2 x0 I 0.435lg D Ом (3) км RсрI x0 I ; 3.5 x1 Ом км






![R – [Ом]](http://s1.studylib.ru/store/data/005005008_1-0b17dcb24ca8b54c0ebd313c9aa9d89d-300x300.png)
