Паросочетания и двудольные графы. Алгоритмы нахождения наибольшего и максимального паросочетания

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
Кубанский государственный технологический университет
(ФГБОУ ВО «КубГТУ»
Институт компьютерных систем и информационной безопасности
Кафедра информационных систем и программирования.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе
По дисциплине Дискретная математика
На тему ” Паросочетания и двудольные графы. Алгоритмы нахождения
наибольшего и максимального паросочетания ”.
Выполнил студент группы 17 – КБ – ПИ1 Савич Ростислав Алексеевич
Допущен к защите:
Руководитель работы__________________________д.ф.-м.н. В. М. Трофимов
(подпись, дата, расшифровка подписи)
Защищен____________________.
Оценка_________________________
(дата)
Члены комиссии____________________________________________________
(подпись, дата, расшифровка подписи)
_____________________________________________________________________________
(подпись, дата, расшифровка подписи)
Краснодар
2018
1
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Кубанский государственный технологический университет»
(ФГБОУ ВПО «КубГТУ»)
Институт компьютерных систем и информационной безопасности
Кафедра информационных систем и программирования
УТВЕРЖДАЮ
Зав. Кафедрой ИСП,
к. т. н., доцент М.В. Янаева
«
»
2018г.
(подпись, дата)
ЗАДАНИЕ
на курсовую работу
Студенту Савичу Ростиславу Алексеевичу группы 17 – КБ – ПИ1 2 курса
ИКСиИБ
Направления 09.03.03 – Прикладная информатика
Тема работы ”Паросочетания и двудольные графы. Алгоритмы нахождения
наибольшего и максимального паросочетания”.
Объем работы:
а) пояснительная записка к работе
с.;
б) рекомендуемая литература: Программирование в алгоритмах / С. М.
Окулов. — М.: БИНОМ. Лаборатория знаний, 2002. — 341 с
Срок выполнения работы: с «4» сентября 2018 г. по « » декабря 2018 г.
Срок защиты:
« » декабря 2018 г.
Дата выдачи задания:
«4» сентября 2018 г.
Дата сдачи проекта на кафедру:
« » декабря 2018 г.
Руководитель работы
Задание принял студент
д.ф.-м.н. В.М. Трофимов
(подпись, Ф.И.О., звание, степень)
(подпись)
2
Р.А.Савич.
Реферат
Пояснительная записка к данной курсовой работе содержит: 17
страниц, 3 изображения, 4 источника.
VISUAL STUDIO 2017, C++, ПРОГРАММА, ДВУДОЛЬНЫЙ ГРАФ,
ПАРОСОЧЕТАНИЕ, АЛГОРИТМ КУНА.
Объектом
исследования
данной
курсовой
работы
является
двудольный граф.
Цель работы состоит в разработке программы для нахождения
наибольшего и максимального паросочетания в двудольном графе.
К полученным результатам относится реализованная и корректно
функционирующая программа.
3
Оглавление
Реферат ..................................................................................................................... 3
Введение ................................................................................................................... 5
1
Постановка задачи ............................................................................................ 6
2
Графы ................................................................................................................. 7
3
Паросочетания ................................................................................................... 9
4
Описание программы ..................................................................................... 11
5
Результат работы программы ........................................................................ 12
Заключение ............................................................................................................ 13
Список использованных источников .................................................................. 14
Приложение А ....................................................................................................... 15
Приложение Б ........................................................................................................ 17
4
Введение
В данной курсовой работе по дисциплине «Дискретная математика»
будет рассмотрена тема паросочетаний в двудольных графах и разработана
программа для нахождения наибольшего и максимального паросочетания.
Данная тема работы актуальна, поскольку графы широко используются в
решении задач математики и информатики. В частности, алгоритмы
нахождения наибольшего паросочетания применяются для нахождения
максимального потока в компьютерных сетях.
5
1 Постановка задачи
Задачей данной курсовой работы является разработка программы для
нахождения наибольшего и максимального паросочетания в двудольном
графе.
6
2 Графы
Граф
—
это
абстрактный
математический
объект,
который
представляет собой множество вершин графа и набор рёбер, которые
соединяют вершины между собой. Например, за множество вершин можно
взять множество населенных пунктов, а в качестве рёбер представить дороги,
соединяющие эти пункты.
Исходя из разных областей применения виды графов могут
различаться направленностью, ограничениями на количество связей и
дополнительными данными о вершинах или рёбрах. Многие структуры,
представляющие практический интерес в математике и информатике, могут
быть представлены графами. Например, строение компьютерных сетей
можно смоделировать при помощи ориентированного графа, в котором
вершины — это компьютеры, а дуги (ориентированные рёбра) —
соединяющие их сети.
Графы являются основным объектом изучения теории графов.
Различают несколько видов графов.
Граф, или неориентированный граф G — это упорядоченная пара
G:=(V,E) G:=(V,E), где V — это непустое множество вершин или узлов, а E
— множество пар (в случае неориентированного графа — неупорядоченных)
вершин, называемых рёбрами.
Ориентированный граф (сокращённо орграф) G — это упорядоченная
пара G:=(V,A), где V — непустое множество вершин или узлов, и A —
множество
(упорядоченных)
пар
различных
вершин,
называемых
ориентированными рёбрами (дугами).
Смешанный граф G — это граф, в котором некоторые рёбра могут
быть
ориентированными,
а
некоторые
—
неориентированными.
Записывается упорядоченной тройкой G:=(V,E,A), где V, E и A определены
так же, как выше.
Ориентированный и неориентированный графы являются частными
случаями смешанного.
7
Двудольный граф или биграф – это граф, множество вершин которого
можно разбить на две части таким образом, что каждое ребро графа
соединяет какую-то вершину из одной части с какой-то вершиной другой
части, то есть не существует ребра, соединяющего две вершины из одной и
той же части.
В данной курсовой работе будет рассмотрен двудольный граф.
8
3
Паросочетания
Паросочетанием в теории графов называют множество попарно
несмежных рёбер, то есть рёбер, не имеющих общих вершин.
Выделяют несколько видов паросочетаний.
Максимальное паросочетание — это такое паросочетание M в графе
G, которое не содержится ни в каком другом паросочетании этого графа, то
есть к нему невозможно добавить ни одно ребро, которое бы являлось
несмежным ко всем рёбрам паросочетания. Другими словами, паросочетание
M графа G является максимальным, если любое ребро в G имеет непустое
пересечение, по крайней мере, с одним ребром из M.
Наибольшее
паросочетание
(или
максимальное
по
размеру
паросочетание)— это такое паросочетание, которое содержит максимальное
количество
рёбер.
У
графа
может
быть
множество
наибольших
паросочетаний. При этом любое наибольшее паросочетание является
максимальным, но не любое максимальное будет наибольшим.
Совершенным паросочетанием называется паросочетание, в котором
участвуют все вершины графа. То есть любая вершина графа инцидентна
ровно одному ребру, входящему в паросочетание. Почти совершенным
паросочетанием называется паросочетание, в котором не участвует ровно
одна вершина. Это может произойти, если граф имеет нечётное число
вершин.
Для нахождения наибольшего паросочетания можно использовать
алгоритм Куна. Этот алгоритм можно описать так: сначала возьмём пустое
паросочетание, а потом — пока в графе удаётся найти увеличивающую цепь,
— будем выполнять чередование паросочетания вдоль этой цепи, и
повторять процесс поиска увеличивающей цепи. Как только такую цепь
найти не удалось — процесс останавливаем, — текущее паросочетание и есть
максимальное.
9
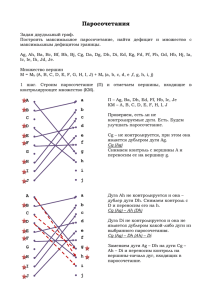
На рисунке 1 представлен рассматриваемый двудольный граф.
Красным выделены ребра, входящие в наибольшее паросочетание, которое
равно 5.
Рисунок 1 Двудольный граф.
10
4 Описание программы
Программа для данной курсовой работы была разработана на языке
программирования С++ в среде разработки Visual Studio 2017
Работа с вводом и выводом данных осуществляется через методы cin
и cout.
Граф был реализован с помощью матрицы смежности.
int Adj[6][6] = {
{1,0,0,0,0,0},
{0,1,1,1,0,0},
{0,0,0,0,1,1},
{0,0,0,0,0,1},
{0,0,0,1,0,0},
{0,0,0,1,0,0} };
Алгоритм Куна.
bool kuhn(int v) {
if (used[v]) return false; used[v] = true;
for (size_t i = 0; i < g[v].size(); ++i) {
int to = g[v][i];
if (mt[to] == -1 || kuhn(mt[to]))
{
mt[to] = v;
return true;
}
}
return false;
}
С помощью setlocale была реализована возможность вывода символов
русского алфавита в консоль.
setlocale(LC_CTYPE, "rus");
Для работы с циклами был использован оператор for.
11
5
Результат работы программы
После написания кода программы, она была запущена для проверки.
Были получены следующие результаты.
12
Заключение
В ходе выполнения данной курсовой работы по дисциплине
«Дискретная математика» была рассмотрена тема графов и паросочетаний, а
также разработана программа для нахождения наибольшего паросочетания в
двудольном графе по алгоритму Куна.
Программа
работает
без
ошибок.
Код
написан
максимально
компактно и интерфейс удобен для использования.
Полученные знания можно применять в дальнейшей деятельности.
13
Список использованных источников
1)
П. Т.А, C/C++. Программирование на языке высокого уровня,
Санкт-Петербург, 2003, p. 461.
2)
www.cyberforum.ru/
3)
Роберт Седжвик. Алгоритмы на графах = Graph algorithms. — 3-е
изд. — Россия, Санкт-Петербург: «ДиаСофтЮП», 2002. — С. 496
4)
Окулов С.М. Программирование в алгоритмах /С.М. Окулов. –
М.: БИНОМ. Лаборатория знаний , 2002.- 341 с.
14
Листинг программы
Приложение А
#include "pch.h"
#include <vector>
#include <iostream>
#include <clocale>
using namespace std;
int n, k;
int p = 0;
vector < vector<int> > g;
vector<int> mt;
vector<char> used;
bool kuhn(int v) {
if (used[v]) return false; used[v] = true;
for (size_t i = 0; i < g[v].size(); ++i) {
int to = g[v][i];
if (mt[to] == -1 || kuhn(mt[to]))
{
mt[to] = v;
return true;
}
}
return false;
}
int main()
{
setlocale(LC_CTYPE, "rus");
n = k = 6;
int Adj[6][6] = {
{1,0,0,0,0,0},
{0,1,1,1,0,0},
{0,0,0,0,1,1},
{0,0,0,0,0,1},
{0,0,0,1,0,0},
{0,0,0,1,0,0} };
for (int i = 0; i < n; i++)
{
g.push_back(vector<int>());
for (int j = 0; j < n; j++)
{
g[i].push_back(0);
g[i][j] = Adj[i][j];
}
}
mt.assign(k, -1);
for (int i = 0; i < n; ++i) {
used.assign(n, false);
kuhn(i);
p++;
}
for (int i = 0; i < k; ++i) if (mt[i] != -1)
15
printf("%d %d\n", mt[i] + 1, i + 1);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cout << Adj[i][j] << " ";
}
cout << endl;
}
cout << "Наибольшее паросочетание: " << p << endl;
}
16
Приложение Б
17