Semakov-SL-Elementy-teorii-veroyatnostei-i-sluchainyh-protsessov

• .• . • • • • • • •
Элементы
теории вероятностей
и случайных процессов
• • • • • • • • • • • • • • • • • • • -• • • • • • • • • • • • • • • • • • • • • • • •
• • •• • • •• •• • • • •• • • • • • • • • • ••• • ••• • • • • • • • • • •
• • • • • • •• • • • • • • • • • •••• • • • •• • • • • • • • •• • • •• •• • • • •• ••
• • • • • • •• • • • • • • • •• • • • • • • • • • • • •• • • • •• • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • • • • • • • «• • • • • • • • • • • • • • • • • • • • • • • • • • • »
МОСКВА
ФИЗМАТЛИТ®
2011
УДК 519.21
ББК 22.171
С 30
С е м а к о в С. Л. Элементы теории вероятностей и случайных процессов. - М.: ФИЗМАТЛИТ, 2011. - 232 с. - ISBN 978-5-9221-1345-8.
Излагаются элементы теории вероятностей и теории случайных процессов.
Много внимания уделяется решению задач, которые занимают большую часть
пособия.
Рекомендовано Учёбно-методическим объединением высших учебных заведений Российской Федерации по образованию в области прикладных математики и физики в .качестве учебного пособия для студентов высших учебных
заведений по направлению «Прикладные математика и физика».
© Ф И ЗМ А Т Л И Т , 2011
ISBN 978-5-9221-1345-8
© С. Л . Семаков, 2011
Часть
§1.
§2.
§3.
§4.
§5.
§6.
§ 7.
§8.
§ 10.
§11.
§ 12.
§ 13.
§14.
§ 15.
6
...............................................................
6
Элементы комбинаторики
Задачи ..............................................................................................................
9
14
Определение вероятности.....................
Задачи ............................................................................
17
Условная вероятность, формулы полной вероятности и Байеса . .
30
35
Задачи. . . . ...................................................................................................
Последовательность независимых испы таний...................................
41
43
Задачи ......................
Случайные величины и функции распределения..............................
50
54
Задачи..............................................................................................................
Числовые характеристики случайной величины . . . .....................
64
76
Задачи............................
Системы случайных величин.........................................
90
93
Задачи ..................................
Закон больших чисел и центральная предельная т е о р е м а
109
113
Задачи. ...............................................................................
Часть
§9.
1. Элементы теории вероятностей ........................................
2.
Элементы теории случайных процессов ....................
Исходные фундаментальные определения, понятия и результаты.
Задачи...................
Математическое ожидание, дисперсия и корреляционная функция
случайного п р о ц е с с а
.................................................................
Задачи...............................................................................................................
Пуассоновский процесс
................................
З адачи.................
Виды сходимости в вероятностном пространстве и характеристики гладкости случайного п роц есса.............................................
Задачи...............................................................................................................
Стационарные и нормальные процессы — два важнейших класса
случайных процессов..................................................................................
Задачи ...................................................................................................
Винеровский проц есс........................
Задачи ..........................................................................................
Интегрирование случайных п р о ц е с с о в ...............................................
Задачи ...............................................................................................................
123
123
128
134
136
142
143
155
161
168
174
189
200
207
214
Пособие состоит из двух частей. В первой части излагаются
элементы теории вероятностей: начальные понятия комбинаторики; определение вероятности; условные вероятности; теоремы
сложения и умножения вероятностей; формулы полной вероятности и Байеса; схема независимых испытаний Бернулли и связанные с ней результаты; понятия случайной величины и функции
распределения, их свойства; числовые характеристики случайной
величины; дискретные и непрерывные распределения; понятия
системы случайных величин и функции совместного распределения; закон больших чисел в формулировке Чебышёва и центральная предельная теорема в форме Ляпунова. Изложение разбито на
восемь параграфов, каждый из которых заканчивается решением
задач различной сложности, соответствующих изучаемой теме.
Во второй части пособия, которая может быть прочитана независимо от первой и требует несколько более серьезной — по сравнению с первой — математической подготовки читателя, рассматриваются вопросы, дающие начальное представление о теории
случайных процессов, а именно: формулируются исходные фундаментальные определения и понятия теории; изучаются свойства
двух важнейших классов случайных процессов — стационарных
и нормальных; подробно рассматриваются пуассоновский и винеровский процессы; определяются виды сходимости в вероятностном пространстве и соответствующие им характеристики гладкости случайных процессов; излагаются вопросы, связанные с интегрированием случайных процессов, в частности, определяется
стохастический интеграл Ито. Изложение второй части разбито
на семь параграфов, каждый из которых заканчивается решением
задач. Задачи — как в первой, так и во второй части пособия —
являются неотъемлемой частью основного текста, во многих случаях содержат важные дополнения к нему и способствуют его
более глубокому пониманию и усвоению.
При написании учебного пособия и отборе предлагаемых примеров и задач автор опирался на две классические работы:
• Феллер В. Введение в теорию вероятностей и ее приложения.
Т. 1, 2. - М.: Мир, 1984;
• Гнеденко Б.В. Курс теории вероятностей: Учебник. Изд. 8-е,
испр. и доп. — М.: Едиториал УРСС, 2005.
Кроме того, использовались монография автора
• Семаков C.JI. Выбросы случайных процессов: приложения
в авиации. — М.: Наука, 2 0 0 5 ^ ,
и сборники формулировок задач, составителями которых являются коллеги автора по кафедре математических основ управления
Московского физико-технического института:
• Основы теории вероятностей и стохастических процессов:
Учебно-методическое пособие / Сост. А.А. Натан, О.Г. Горбачев, С.А. Гуз, Е.В. Бурнаев, А.В. Гасников. — М.: МФТИ,
2006;
• Случайные процессы: Учебно-методическое пособие / Сост.
А.А. Натан, О.Г. Горбачев, С.А. Гуз, Е.В. Бурнаев, А.В. Гасников. — М.: МФТИ, 2006.
Многие из представленных в пособии задач разбирались автором
на семинарах со студентами Московского физико-технического
института.
W В этой монографии (ее ядром являются оригинальные результаты
автора, опубликованные в журналах «Теория вероятностей и ее применения», «Известия РАН. Теория и системы управления», «Автоматика
и телемеханика», «Ученые записки ЦАГИ» и др.) излагается взгляд на
теорию случайных процессов как инструмент математического моделирования. Известный специалист по математическому моделированию
сложных систем, академик РАН А.А. Петров охарактеризовал монографию, в частности, так: «... изложенный материал дает образцовое
представление о том, как надо применять методологию математического
моделирования к решению сложных прикладных задач».
§ 1. Элементы комбинаторики
Рассмотрим строку из k элементов (x\,x<i, . .. ,x*.)- Будем считать, что элемент х\ может быть выбран из некоторой совокупности различных элементов, общее число которых равно щ, т. е.
элемент х\ может быть выбран п\ способами. Аналогично будем
считать, что элемент Х2 (который также выбирается из определенной совокупности элементов) при ранее выбранном элементе х\
может быть выбран щ способами, и т.д. Наконец, элемент хк
при ранее выбранных элементах Х\,Х2 , . . . , Х к - \ может быть выбран Пк способами. Поставим вопрос: сколько N различных строк
{Х[,Х2 , . . . ,Xk) М О Ж Н О при ЭТО М составить? Строки {Х\,Х2 , . . . ,Xk)
и (xi,X 2 , . . . ,Хк) по определению различны, если хотя бы для
одного г, где i — 1,2, .. . ,k, х,- Ф х,-. Покажем, что
N = П\Щ . . . rtfe.
Действительно, если k = 2, то утверждение очевидно: оно легко проверяется перебором. Пусть k = 3. Рассмотрим пару (хьхг)
как элемент нового типа. Существует ЩП2 таких пар и щ элементов хз. Каждая тройка (х ^х г.х з) может рассматриваться как
пара, состоящая из (хь хг) и хз. Значит, число троек равно щ щ щ .
Доказательство утверждения для любого k получается по методу
математической индукции.
Доказанное утверждение иногда называют комбинаторным
правилом произведения.
Пример 1. Сколько способов разместить г шаров в п ящиках?
Все шары и все ящики различны, в любом ящике может оказаться
любое число шаров, в том числе нулевое.
Перенумеруем все шары и отдельно все ящики. Каждому размещению шаров по ящикам поставим в соответствие строку из г
позиций, где в 1-й позиции стоит номер ящика, в котором оказал-
ся 1-й шар, во 2-й позиции — номер ящика, в котором оказался
2-й шар, . . . , в r -й позиции — номер ящика, в котором оказался
г-й шар. Тогда число размещений будет равно числу различных
строк, которое, в свою очередь, по правилу произведения равно
п • п • . . . • п = п г.
4------ v------ '
г сомножителей
Определение 1. Число способов расположить п различных
элементов в ряд называется числом перестановок из п элементов
и обозначается Рп.
Покажем, что Рп = п\, где п! есть, по определению, произведение всех натуральных чисел от 1 до п: п! = 1 • 2 • 3 • . . . • п;
при этом, по определению, 0! = 1. Действительно, каждому расположению элементов в ряд соответствует строка из п позиций,
где на первой позиции расположен элемент, занимающий первое
положение в ряду, на второй позиции — элемент, занимающий
второе положение в ряду, и т. д. Ясно, что соответствие взаимно
однозначное, так что число способов расположить п элементов
в ряд будет равно числу различных строк. На первую позицию
в строке можно поставить любой из имеющихся п элементов; при
заполненной первой позиции на вторую позицию можно поставить любой из оставшихся (п — 1) элементов и т. д. В результате
по правилу произведения получим, что число различных строк
равно
п • (п — 1) • (п - 2) • . . . • 2 • 1 = /г!,
что и требовалось доказать.
Определение 2. Числом сочетаний из п элементов по k элементам называется число способов выбрать k элементов из п элементов без учета порядка следования элементов в выборке. Это
число, как правило, обозначается С*.
В качестве примера найдем С |. Пусть для наглядности элементами, число которых п = 3, являются геометрические фигуры:
квадрат, треугольник и круг. Тогда из этих трех фигур две фигуры (k = 2) можно выбрать следующим образом: квадрат и треугольник, квадрат и круг, треугольник и круг, т. е. числом способов, равным 3. Таким образом, Cf = 3.
Покажем, что при произвольных п и k, k < п, число
может
быть вычислено по формуле
r*k
_
п ” k\(n-k)V
Выберем k элементов из п элементов и будем располагать их
в строку в различном порядке. Получим k\ различных строк. Тогда общее количество различных строк из k позиций, которое
можно составить из п элементов, равно k\C„. С другой стороны, это количество строк можно найти по правилу произведения: на первую позицию можно поставить любой из п элементов, на вторую — любой из оставшихся (п — 1) элементов,
на k -ю позицию — любой из оставшихся (ti — (k — 1)) элементов.
Следовательно,
k\ Ckn = п(п - 1)(я - 2 ) . . . (л - (Л - 1)),
откуда
г к _ п(п ~ !)(« - 2) . . . (л - (А; - 1))
Ln~
ki~
~
или, домножая числитель и знаменатель дроби на (п —k)\, получаем
pk_
п ~ k\(n-k)V
что и требовалось доказать.
Пример 2. Каждая кость домино помечается двумя числами.
Сколько различных костей можно образовать, если использовать
натуральные числа 1, 2, . . . , л?
Поскольку числа на костях домино не упорядочены, то количество различных костей без учета дублей (дубль — кость домино, помеченная одинаковыми числами) — это количество способов выбрать два числа из п чисел без учета порядка выбираемых
чисел, т. е. С%. А так как число дублей равно п, то с их учетом
число различных костей домино равно С„ + п. В частности, при
п = 6 получим С | + 6 =
+ 6 = 21.
Определение 3. Числом размещений из п элементов по k
элементам называется число способов выбрать k элементов из
п элементов с учетом порядка следования элементов в выборке.
Это число обычно обозначается А*.
В качестве примера найдем А\ . Пусть, как и выше, элементами, число которых п = 3, являются геометрические фигуры:
квадрат, треугольник и круг. Тогда из этих трех фигур две фигуры (k = 2) с учетом порядка можно выбрать следующим образом:
квадрат и треугольник, треугольник и квадрат, квадрат и круг,
круг и квадрат, треугольник и круг, круг и треугольник, т. е.
числом способов, равным 6 . Таким образом, А | = 6.
При произвольных п и k, k < п, число
лено по формуле
может быть вычис-
A* = n ( n - l ) . . . ( n - ( k - 1)) =
которая следует из правила произведения. Отметим также, что
A kn = CknPk.
Пример 3. Имеются 5 различных автомобилей. Сколько способов можно предложить, чтобы посадить двух человек в эти
автомобили, если в каждый автомобиль можно посадить только
одного человека?
Пусть I и II — упомянутые два человека. Человека I будем
сажать в первый выбранный автомобиль, а человека II — во вто5!
рой. Тогда различное число рассадок есть Л | = ^ = 20 — число
j!
способов выбрать два автомобиля из пяти с учетом порядка выбираемых автомобилей.
Задачи
1. В азбуке Морзе буквы представляются последовательностями тире и точек с возможными повторениями. Сколько букв
можно составить из пяти или менее символов?
Р е ш е н и е . Из одного символа можно составить 2 буквы, из k
символов по правилу произведения можно составить 2k букв. Следовательно, число букв, которые можно составить из пяти или
менее символов, равно
2 + 22 + 23 + 24 + 25 = 2 + 4 + 8 + 16 + 32 = 62.
2 . Сколькими способами можно расположить в ряд т белых
и k черных шаров?
Р е ш е н и е , а) Будем сначала предполагать, что все шары одного цвета неразличимы. Расположение полностью определится,
если указать позиции, в которых будут находиться белые (черные) шары. Эти позиции можно выбрать C™+k (C*+ft) способами.
Следовательно, искомое число способов есть C™+k = C^+k.
б) Будем теперь считать, что шары одного цвета различимы;
для этого их, например, можно перенумеровать. Число способов
выбрать позиции расположения белых шаров равно C™+k. В эти
позиции белые шары можно расставить т\ способами, а в остав-
шиеся позиции черные шары можно расставить k\ способами. Значит, искомое возможное число расположений есть
C™+km\k\ = {m + k)\.
Заметим, что в случае б), когда все шары различимы, задача
сводится к нахождению числа перестановок из (т + k ) различных элементов, так что полученный результат (т + k)\ становится
очевидным.
3. Сколько существует различимых способов размещения г
неразличимых предметов (например, одинаковых по цвету и размеру шаров) по п различимым ящикам?
Р е ш е н и е . Каждому размещению шаров поставим в соответствие цепочку цифр, состоящую из 0 и 1, следующим образом.
Сначала пишем 0 , затем число единиц, равное числу предметов
в первом ящике, затем 0 , затем число единиц, равное числу предметов во втором ящике, затем 0, и т.д. При этом общее число
единиц будет равно г, а общее число нулей, которые играют роль
разделителей, будет равно п + 1. Например, последовательность
011001011100
соответствует размещению 6 предметов по 5 ящикам следующим
образом: в первом ящике — два предмета, во втором — ни одного,
в третьем — один, в четвертом — три, в пятом — ни одного. Первая и последние цифры — всегда нули, а промежуточные — либо
нули, либо единицы. Размещение предметов однозначно определится, если будет указано, какие из промежуточных позиций занимают единицы. Поскольку число промежуточных позиций равно г + п — 1, а число единиц равно г, то число возможных вариантов будет равно Сгг+п_ х.
4. Сколько существует размещений в условиях задачи 3, при
которых ни один ящик не остается пустым? Предполагается, что
г > п.
Р е ш е н и е . Первый способ. Условие, что ни один из ящиков
не оказался пустым, означает, что нет двух стоящих рядом нулей. Между г единицами имеются (г — 1) промежутков, в (п — 1)
из которых помещено по одному нулю. Следовательно, имеется
С*~у вариантов выбора.
Второй способ. Положим сначала в каждый ящик ровно по
одному предмету. А затем посчитаем, сколько способов распределить оставшиеся (г —п) предметов по п ящикам. Это число
способов, как следует из решения задачи 3, равно Cr^ n^ n_ v что
совпадает с C^Z\ •
5.
Найти число различимых способов размещения г\ неразличимых предметов одного вида и Г2 неразличимых предметов
другого вида по п различимым ящикам.
Р е ш е н и е . Зафиксируем какой-либо способ размещения г\
предметов одного вида и будем перебирать различные способы
размещения Г2 предметов второго вида. Этих способов, как следует из решения задачи 3, будет Crr*+n_ v Но способов размещения
предметов первого вида будет Сгг1^ п_ {. Следовательно, искомое
число способов равно
ГГЧ
п г1
ь г2-рл-1 ' 4 ,+ л -Г
6 . Сколько существует различимых результатов бросания г
неразличимых игральных костей?
Р е ш е н и е . Результат бросания г костей можно разбить на
шесть подгрупп: в 1-ю подгруппу попадут г\ костей, на которых
выпали «1», во 2-ю — r<z костей, на которых выпали «2», . . . ,
в 6-ю подгруппу — Гб костей, на которых выпали «6». При этом
r\ + f 2 + ■■■+ Гб = г. Поэтому результатов бросания г костей может быть столько, сколько способов распределить г неразличимых предметов по 6 различимым ящикам, т. е. (см. решение задачи з) с^+6_! = с ;+5.
7. Сколько существует различимых результатов бросания
г монет?
Р е ш е н и е . Результат бросания г монет можно разбить на две
подгруппы: в первую попадут все монеты, на которых выпал герб,
а во вторую — все монеты, на которых выпала решка. Поэтому
результатов бросания г монет может быть столько, сколько способов распределить г неразличимых предметов по двум различимым
ящикам, т. е. (см. решение задачи 3) Crr+2_i = С£+1 = г + 1.
8 . Сколько чисел, заключенных между 1000 и 9999, содержат
цифру 3?
Р е ш е н и е . Первый способ. Числа от 1000 до 9999 включительно — это все четырехзначные числа. Всего таких чисел 9000
штук. Действительно, каждому четырехзначному числу можно
сопоставить строку из четырех позиций, где первую позицию занимает первая цифра числа, вторую — вторая и т. д. По правилу
произведения число различных строк (которое равно числу различных четырехзначных чисел) равно 9 • 10 • 10 • 10 = 9000, ибо
в первую позицию можно вписать любую цифру от 1 до 9, а во
вторую, третью и четвертую позиции — любую цифру от 0 до 9,
так что первую позицию можно заполнить 9 способами, а вторую,
третью и четвертую — 10 способами.
Рассуждая аналогично и используя правило произведения, находим число всех четырехзначных чисел, не содержащих цифру 3:
оно равно 8 • 9 • 9 • 9 = 5832. Следовательно, число всех четырехзначных чисел, содержащих цифру 3, равно N = 9000 —5832 = 3168.
Второй способ. Пусть N\ — число всех четырехзначных чисел, содержащих в своей десятичной записи ровно одну цифру 3,
N 2 — ровно две цифры 3, Л/з — ровно три цифры 3, N 4 — ровно
четыре цифры 3. Тогда N = N\ + N 2 4- Л/3 + N 4 , причем, очевидно,
N 4 = 1.
Найдем N\. Сюда относятся все четерехзначные числа вида
3-----, где пустые позиции (прочерки) могут быть заняты любыми
цифрами кроме цифры 3. Таких чисел, по правилу произведения,
9 • 9 • 9 = 729. Кроме того, к Ni относятся все четырехзначные
числа видов - 3 — , — 3 - , ----- 3, где пустые позиции по-прежнему
могут быть заняты любыми цифрами, за исключением цифры 3,
причем если позиция первая, то она не может быть занята цифрой 0. По правилу произведения четырехзначных чисел вида - 3 —
будет 8 • 9 • 9 = 648 штук, столько же будет чисел вида — 3 - и чисел в и д а
3. Таким образом, N\ = 729 + 3 • 648 = 2673.
Аналогично найдем число N 2 . Сюда относятся все четырехзначные числа видов 33— , 3 -3 -, 3— 3, -3 3 -, -3 -3 , — 33, где
пустые позиции могут быть заняты любыми цифрами за исключением цифры 3, причем если позиция первая, то она не может быть занята цифрой 0. По правилу произведения чисел видов 33— , 3 - 3 - и 3— 3 будет по 9 • 9 = 81 штуке, а чисел видов
- 3 3 -, - 3 - 3 и — 33 будет по 8 • 9 = 72 штуке. Следовательно,
N 2 = 3 • 81 + 3 • 72 = 459.
Осталось найти Л/3. Сюда относятся числа видов 333-, 33-3,
3-33 и -333. Чисел первых трех видов будет по 9 штук, а чисел
вида -333 будет 8 штук. Значит, Л/3 = 3 • 9 + 8 = 35.
Таким образом,
N = М + N 2. + Л/з + N 4 = 2673 + 459 + 35 + 1 = 3168.
9.
Сколькими способами можно рассадить п человек за круглым столом?
Р е ш е н и е . Перенумеруем все места. Пусть наблюдатель А
знает нумерацию мест, а наблюдатель В — нет. Предполагается,
что все места одинаковы, так что в задаче спрашивается, сколько
различных рассадок может быть с точки зрения наблюдателя В.
Обозначим это число через К. Если всех сидящих сдвинуть на
одно место по кругу, то с точки зрения наблюдателя В способ
рассадки людей не изменится. Поэтому п рассадкам с позиции
наблюдателя А будет соответствовать одна и та же рассадка с позиции наблюдателя В. Но с позиции наблюдателя А число рассадок равно «!, так что К ■п = п\, откуда К = (п —1)!.
10. Сколько различных делителей у числа Pj' p^2
где
Pi,p 2 , ■■■,Pk — различные простые числа?
Р е ш е н и е . Любой делитель имеет вид
рТ рТ
где т \, т 2 ........ /и* — неотрицательные целые числа, такие, что
Щ < Щ, m 2 < П2 , .. ■, rrik < щ. Каждому делителю поставим в соответствие строчку (т \, т 2 ,
Тогда число различных делителей будет равно числу различных строк указанного вида.
В качестве mi может быть взято любое из чисел 0,1,2,
т. е. элемент т\ может быть выбран (п\ + 1) способами. При выбранном элементе т\ элемент m 2 может быть выбран (щ + 1) способами, . . . , при выбранных элементах m i, m 2 , ...,/re*_i элемент
может быть выбран (щ + 1 ) способами. Следовательно, по
правилу произведения число различных строк, а значит, и число
различных делителей будет равно (щ + 1)(я2 + 1) . . . (n* + 1).
Рассмотрим практическую ситуацию, связанную со случайным экспериментом, т. е. с некоторым испытанием Е, исход которого определяется случайным механизмом, воздействие которого
заранее предсказать невозможно. Будем интересоваться какимлибо событием А, связанным с £ в том смысле, что в результате Е событие А может произойти, а может не произойти. Во многих жизненных ситуациях возникает необходимость попытаться
предсказать степень возможности реализации события А в результате Е. Эту степень возможности будем характеризовать числом Р{А} — вероятностью события А, которую определим следующим образом.
1.
Рассмотрим сначала случай, когда при каждом испытании Е возможны п несовместных и равновозможных исходов
А[, А 2 , .. ■, А п и только они. Несовместность исходов означает,
что никакие два исхода одновременно, т. е. в одном испытании,
произойти не могут. В этой ситуации любое событие А, связанное
с Е, означает, что в результате Е имел место один из исходов
Aix,Ai2, . . . , A i m. При этом каждое конкретное событие А будет
определяться своим числом т е {0 , 1, 2, . . . , « } и своим набором
чисел г'ь «2, . . . , im € {1, 2, . . . , « } . Положим по определению
Р{А} = - .
п
Особо отметим два частных случая события А. Первый —
событие А происходит всегда при проведении Е. В этом случае
событие А будем называть достоверным. Ему соответствуют значение т = п и вероятность Р{А} = 1. Второй случай — событие А
никогда не происходит при проведении Е. В этом случае событие А будем называть невозможным. Ему соответствуют значение т = 0 и вероятность Р { А } = 0. Достоверное событие принято
обозначать символом П, невозможное — символом 0. Кроме того,
введем понятие противоположного события. Событие А будем называть противоположным событию А, если оно состоит в том,
что А не произошло.
Введенное выше определение вероятности называется классическим.
Пример I. Пусть эксперимент Е состоит в бросании на плоскость геометрически правильного кубика, изготовленного из однородного материала. Если пронумеровать грани цифрами от 1
до 6, то при бросании кубика могут произойти шесть равновозможных событий (и только они): А\ — выпадение грани 1, А 2 —
выпадение грани 2 , А$ — выпадение грани 6. Пусть событие А
означает, что выпала грань с четным номером, т. е. произошло
какое-либо из событий A 2 , A 4 ,Aq. Следовательно, т = 3 (ii = 2,
h = 4, г’з = 6) и Р { А } = т /п = 3/6 = 1/2.
2.
Распространим введенное выше определение на случай,
когда с экспериментом Е связано бесконечное число равновозможных исходов. Предположим, что каждому результату эксперимента Е можно взаимно-однозначно сопоставить точку в некоторой области G (на прямой, на плоскости, в пространстве). При
этом изучаемому событию А, связанному с Е, будет соответствовать попадание точки в некоторое подмножество g С G. Если
все точки области G равновозможны в смысле попадания в них
в результате эксперимента, то вероятность попасть в какую-либо
часть области G пропорциональна мере (длине, площади, объему)
этой части и не зависит от ее расположения и формы. В этом
случае, по определению,
Р{А} = = 1 .
mes и
Такой подход к определению вероятности называется геометрическим.
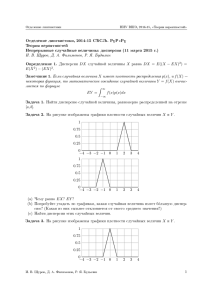
Пример 2. Предположим, что два человека А и В договорились встретиться в определенном месте между 12 и 13 часами.
Пришедший первым ждет второго в течение 20 мин., после чего
уходит. Чему рана вероятность встречи, если приход каждого
в течение указанного часа может произойти с равной возможностью в любой момент, причем момент прихода одного лица не
влияет на момент прихода другого?
Пусть х — момент прихода лица А, а у — момент прихода
лица В; х и у будем отсчитывать в минутах от 12 ч. Тогда необходимое и достаточное условия встречи дает неравенство
\х - у \ < 20,
а проведение эксперимента (приход двух людей к месту встречи) можно интерпретировать как вбрасывание точки в квадрат
со стороной 60 (рис. 1): абсцисса х точки даст момент прихода
человека А, ордината у — момент прихода человека В. Точки,
Рис. 1
благоприятствующие встрече, расположатся в заштрихованной
области на рисунке. Искомая вероятность будет равна отношению
площади заштрихованной фигуры к площади всего квадрата, т. е.
602 - 402
5
602
“ 9'
3. Описанные выше подходы к определению вероятности применимы только в том случае, когда с экспериментом Е можно связать множество равновозможных исходов, которые исчерпывают
все результаты эксперимента. Этого недостатка лишен аксиоматический подход, предложенный А.Н. Колмогоровым.
Исходным пунктом аксиоматики Колмогорова является множество П, элементы которого называются элементарными событиями. Затем вводится в рассмотрение множество Т подмножеств элементарных событий. Элементы множества Т называются событиями, при этом под операциями над событиями понимаются операции над соответствующими множествами. В табл. 1
представлено соответствие между языком теории множеств и языком теории вероятностей.
Множество Т называется алгеброй множеств (на Г2), если
выполняются следующие условия:
1) П € Т , 0 е Т \
2) если А € Т , то и А е Т \
3) если Л G f и В е f , то A \J В Е Т vl А с \ В £
если дополнительно к перечисленным выполняется еще условие:
4) из того, что А п € Т для любого « = 1 ,2 ,..., следует, что
\JAn € Т ,
п
^ 3"’>
п
то множество Т называется а-алгеброй.
Таблица 1
Термины
Обозначения
теории множеств
теории вероятностей
О
множество, пространство
пространство элементарных событий, достоверное событие
W
элемент множества
элементарное событие
А, В
подмножество А, В
случайное событие А, В
АиВ=А+В
объединение
множеств А и В
сумма событий А и В
А ПВ = АВ
пересечение
множеств А и В
произведение событий А
иВ
А
дополнение
ства Л до О
событие, противоположное событию А
0
пустое множество
невозможное событие
А ПВ = АВ = 0
множества А и В не
пересекаются
события А и В несовместны
А =В
множества А и В равны
события А и В равносильны
множе-
Аксиома 1. Каждому событию А поставлено в соответствие неотрицательное число Р { А }, называемое его вероятностью.
Аксиома 2 . Р {Щ = 1.
Аксиома 3. Если события А \ ,А 2 , . • • Ап> • • • попарно несовместны, то
Р { А Х+ А 2 + . . . + А п + . . . } = P{Ai} + P{A 2} + . . . + Р { А п} + . . . .
Тройка объектов (С1, Л,Р), где С1 — множество элементарных
событий, Т — сг-алгебра подмножеств С1 (называемых событиями), Р{А } — вероятность, определенная на и-алгебре Т , называется вероятностным пространством.
Задачи
1.
В урне находятся N одинаковых по размеру и внешнему виду шаров; среди них М белых и {N — М) черных. Наудачу вынимают п шаров (без возвращения в урну). Чему равна вероятность
того, что среди них окажется т белых?
Р е ш е н и е . Общее число равновероятных исходов равно Сдг,
из них число благоприятных
так что искомая вероятность равна
рт
р п —т
ь N -M
2. Какова вероятность при 24 бросаниях по две игральные
кости получить хотя бы один раз две единицы?
Р е ш е н и е . Пусть событие А состоит в том, что хотя бы один
раз выпали две единицы при 24 бросаниях двух игральных костей. Тогда событие А означает, что ни разу не выпали две единицы. Воспользуемся классическим определении вероятности, согласно которому Р { А } = n /N , где N — общее число равновозможных исходов, п — число благоприятных (т. е. приводящих к событию А) исходов. Поскольку при одном бросании двух игральных костей возможны 36 равновероятных результатов, причем
только один из них приводит к выпадению двух единиц, то по
правилу произведения N = 3624, а п = (36 — I)24 = 3524. Искомая
вероятность
Р{А} = 1 - Р{А) = 1 - £ = 1 -
= 0,4914 . . . .
3. Партия продукции состоит из 10 изделий, среди которых
2 изделия дефектные. Какое наименьшее число k изделий необходимо проверить, для того чтобы среди них с вероятностью не
меньше 0,9 содержалось хотя бы одно дефектное?
Р е ш е н и е . Пусть событие А состоит в том, что среди k выбранных было хотя бы одно дефектное изделие. Тогда событие А
означает, что все k выбранных изделий — нормальные (т. е. не
имеющие дефектов). По классическому определению вероятности
Р{А} = n /N , где N = С — общее число равновозможных исходов, которое в данном случае равно числу способов выбрать k
элементов из 10 элементов, 2, п — С\ — число благоприятных (т. е.
приводящих к событию Р{А}) исходов, которое в данном случае
равно числу способов выбрать k изделий из 10 —2 = 8 нормальных изделий. Таким образом,
Р{А} = \ - Р { А } ^ \ - ^ .
Чо
По условию Р{А} > 0,9, т. е.
откуда
k 2 - т + 81 < о.
Целые положительные k, удовлетворяющие этому условию и ограничению k < 10, — это числа 7, 8, 9, 10. Значит, искомое k = 7.
4.
Найти вероятность того, что из 50 студентов, присутствующих на лекции, хотя бы двое имеют одну и ту же дату рождения.
Р е ш е н и е . Будем считать, что в году 365 дней. Общее число N
равновозможных вариантов распределения дней рождения в году
может быть найдено по комбинаторному правилу произведения:
N = 36550.
Пусть т — число вариантов, когда все родились в разные дни. По
правилу произведения
т = 365 • 364 •
• (365 - 49) = Л ^ 5.
По классическому определению вероятности искомая вероятность
равна
JV—tn
N~
^
365 364
~ 365 ' 365
5.
Группа из п человек разного роста случайным образом выстраивается в шеренгу. Найти вероятность того, что самый высокий и самый низкий окажутся рядом.
Р е ш е н и е . Общее число расстановок людей в шеренгу равно п\. Число благоприятных расстановок можно подсчитать, если
пару «низкий-высокий» условно рассматривать за один объект.
Тогда число благоприятных расстановок будет равно (п — 1)! • 2,
где коэффициент 2 учитывает то обстоятельство, что самый низкий и самый высокий, стоящие рядом, могут поменяться местами.
Искомая вероятность равна
{число благоприятных расстановок} _ 2 • (п — 1)! _ 2
п\
п
{общее число расстановок}
6.
Группа из п человек разного роста случайным образом выстраивается в шеренгу. Найти вероятность того, что между самым высоким и самым низким расположатся более k человек.
Р е ш е н и е . Общее число расстановок людей в шеренгу равно п\. Найдем число расстановок, когда между самым низким
и самым высоким ровно (k + 1 ) человек. Обозначим это число
через Nk+i. Тогда по схеме
1
'
2
3
k
k+ l
k+ 2
'
k+ 3
п
(АН-1) человек
где X и Y — самый низкий и самый высокий, нетрудно сообразить,
что
N k+1 = 2 • (п - 2)! • (п - (k + 3) +1) = 2 • (п - 2)! • (п - k - 2).
'------ V------ '
число сдвиж ек
Здесь 2 • (п —(k + 3) + 1) — число способов зафиксировать двух
определенных человек в шеренге из п человек так, чтобы между
ними было ровно (k + 1) человек; (п — 2)! — число способов разместить оставшихся (п — 2) человек по (п — 2) свободным местам.
Коэффициент 2 в формуле для N^+\ учитывает то обстоятельство,
что X и Y можно поменять местами, не меняя при этом положения
остальных людей.
Аналогично,
N k+2 = 2 •(п - 2)! • (п - (k + 4) + 1) = 2 • (п - 2)! • (п - k - 3),
з = 2 •(л - 2)! • (л - (п - 3 + 2) + 1) = 2 • {п - 2)! • 2,
JV„_2 = 2 •(п - 2)! • (п - (л - 2 + 2) + 1) = 2 • (п - 2)! • 1.
Следовательно, число расстановок т, когда между самымвысоким и самым низким будет более k человек, равно
т = А/&+1 + Nk +2 + • • • + Afn_2 =
2 • (n —2 ) \ - i =
i=i
= 2 • (n - 2)!
2 г = 2 • (n - 2)! • l ±
i=
? ~ k ~ 2
,(n - k -
2)
=
1
= (n — 2)! (n —k — 1)(n — k — 2).
В результате для искомой вероятности имеем по классическому
определению
(п - 2)! ( n - k - 1)(п - k - 2 ) _ ( n ~ k - 1){п - k - 2)
7.
Из колоды, содержащей 52 карты, наугад берутся 6 карт.
Какова вероятность того, что среди них будут представлены все
четыре масти?
Р е ш е н и е . Общее число равновозможных выборов равно С |2Найдем число благоприятных выборов. С этой целью перенумеруем масти: I, И, III, IV. Все благоприятные выборы можно разбить
на 10 типов:
тип 1 — I II, III, IV, I, I;
тип 2 — 1 II, III, IV, I, II;
тип 3 — 1 II, III, IV, I, III;
тип 4 — 1 II, III, IV, I, IV;
тип 5 — I II, III, IV, II, II;
тип 6 — I II, III, IV, II, III;
тип 7 — 1 II, III, IV, II, IV;
тип 8 — 1 II, III, IV, III, III;
тип 9 — 1 II, III, IV, III, IV;
тип 10 - I, II, III, IV, IV, IV.
Пусть Ni — количество различных выборов г-го типа, i =
= 1,2, . . . , 10. Тогда
N l = N 5 = N s = м о = С?з • С\3 • С\з • С}3,
щ = N 3 = V4 = N 6 = М7 = N 9 = Cf 3 ■Cf 3 • C\ 3 ■C\3,
так что искомая вероятность равна
Ni + N2 + ... + N10 4С?зС|зС{зС}з + бС^С^С'зС'з
133 • 38___ _
с |2
"
с562
- 4 7 .49 . 5 -1 7 = 0,426 . . . .
8.
Каждая из п палок одинаковой длины разламывается на две
части —длинную и короткую — так, что все длинные (а значит,
и все короткие) обломки одинаковы по своей длине.Полученные обломки, число которых составляет 2п, случайным образом
объединяют в пары, каждая из которых образует новую палку.
Найти вероятность того, что: а) все обломки объединяются в первоначальном порядке, образуя исходные палки; б) все длинные
обломки объединяются с короткими.
Р е ш е н и е . Найдем сначала общее число равновозможных
исходов — число способов из 2п обломков составить п палок,
когда любой из обломков можно соединить с любым. Число таких
способов с учетом порядка появления палок равно
г 2
г 2
г 2
г 2
_ (2 пУ-
с 2п ‘ с 2л -2 ' и 2 л -4 ' • • • ' и 2 —
2"
’
а без учета порядка (т. е. если нас интересует только конечный
набор образовавшихся палок без учета порядка, в котором они
появлялись)
(2 п)\/ 2 п _ (2л)!
я!
~ п\ 2 п '
В случае а) благоприятный вариант (без учета порядка), очевидно, только один, так что в этом случае искомая вероятность равна
1
_ л!2"
(2я)!/(я!2") ~ (2л)!'
В случае б) число благоприятных вариантов объединения с учетом порядка появления палок равно
(С1п •С\) •(С‘_, • С ф ) . (С\ _ 2 • С‘_2) . . . (С} • С\)= (л!)2.
Здесь (С* •ф —число способов выбрать«правильную»
(длинный обломок + короткий обломок) первую пару, (Cln_j • С\_ j) —
число способов при выбранной «правильной» первой паре выбрать
«правильную» вторую пару, (С1п _ 2 ■Схп_2) — число способов при
выбранных «правильных» первой и второй парах выбрать «правильную» третью пару, и т.д. Число благоприятных вариантов
объединения без учета порядка равно
Последний результат можно получить и по-другому. Расположим
все длинные обломки напротив коротких. Зафиксируем порядок
следования длинных обломков, а короткие обломки будем переставлять и затем состыковывать их с длинными, расположенными напротив. Тогда, очевидно, число различных вариантов объединения будет равно числу возможных перестановок коротких
обломков, т. е. ровно п\.
Таким образом, по классическому определению вероятности
искомая вероятность в случае б) равна
п\
(л!)22"
2 - 4 - 6 ... 2п
(2 п)\/{п\ 2 п) ~ (2л)! _ (я + 1)(л + 2) . . . 2л'
9.
Стержень длиной / разрезан в двух случайно выбранных
точках. Найти вероятность того, что из получившихся трех отрезков можно составить треугольник.
Р е ш е н и е . Пусть х — длина первого отрезка, у — длина
второго. Тогда длина третьего отрезка равна I — (х + у). Ясно,
что должны быть выполнены условия: х > 0 , у > 0 , х + у < /, так
что результат разрезания стержня можно интерпретировать как
выбор произвольной точки из треугольника, изображенного на
рис. 2: выбор точки М означает, что длина первого отрезка (под
которым можно условиться понимать, например, левый обломок
стержня) равна х, длина второго (под которым можно понимать
правый обломок) равна у, а длина третьего (т. е. среднего обломка) равна / —(х + у). Из полученных отрезков можно составить
треугольник тогда и только тогда, когда длина любого из отрезков
будет меньше суммы длин двух других, т. е. когда
х < у + (I — х — у)
у < х + (1 —х —у)
I — х — у < х + у,
или
(х <
<у <
Уу >
1/2
1/2
1/2
— х.
Рис. 2
Последняя система определяет треугольник, заштрихованный
на рис. 3.
Следовательно, в соответствии с геометрическим подходом
к подсчету вероятности искомая вероятность Р может быть вычислена как отношение площади 1/2 - //2 - //2 заштрихованного
треугольника к площади 1/2 • / • / большого треугольника:
i l l
Р= 2 ' 2 ' 2 _ I
2
10.
В гардеробе все шляпы N посетителей оказались случайным образом перепутанными. Шляпы не имеют внешних отличительных признаков. Какова вероятность того, что хотя бы один
посетитель получит свою шляпу?
Р е ш е н и е . Предварительно докажем следующую теорему
о вероятности суммы п событий.
Теорема. Вероятность Р{А\ + . . . + А п} осуществления хотя бы одного из событий А и •.. А п равна
Р{А\ + . .. + А п} = ^ 2 P{Ai\} ~
/i= l
+
Е
P{AhAi2} +
\ < i \ < i 2< n
P{AixAi2Ai3} -
1 < i 1 < /2 < i 3 < n
E
P{AiiAi2Ai3Ai4} + . . .
1 < i 1 < i2 < is < /4 < n
. . . + ( - l )"+1
Y,
P { A kA h . . . A in}.
\ < i X< i 2 < . . . < i n < n
Условие 1 < i\ < /2 < h < - - - < n означает, что в суммах каждая комбинация событий встречается ровно один раз; следовательно, сумма
Е
P { A hAi2 . . . A i m},
1<Ч<*2< —<*т<Я
т < п,
содержит С% слагаемых, а последняя сумма
Е
P { A hA h . . . A in}
\ < i \ < i 2< ...< in < n
сводится к единственному слагаемому
Р{ А \А 2 ■■. А п},
которое является вероятностью одновременного осуществления
всех п событий.
Ниже приведены утверждения теоремы для частных случаев
п = 2,3,4. При п — 2:
Р { А Х+ А 2} = Р{А\} + Р{А 2} - Р { А ХА 2}.
При п = 3:
Р { А ! + Л 2 + Л 3} = Р { А !} + Р { А 2} + Р{А 3} - {Р{АХА 2} + Р { А ХА 3] + Р{А2Л3}) + Р { А \ Л 2Л 3}.
При л = 4:
Р{Л ! + Л2 + Л3 + Л 4} = Р{Л !} + Р{А2} + Р{А3} + Р{Л4} - (Р{АХА 2} + Р { А ХА 3} + Р { А х А а} + Р{Л2Л 3} + Р{А 2А а} +
+ Р { А 3А а}) + Р { А ХЛ 2Л 3} + Р { А хА 2А а} + Р { А хА 3А а} +
+ Р{Л2Л 3Л4} - Р { Л 1Л 2Л 3Л 4}.
Д о к а з а т е л ь с т в о теоремы проведем по методу математической индукции. При п = 2 утверждение теоремы очевидно.
Пусть оно выполняется при п = k. Покажем, что тогда оно будет
выполняться и при п = k + 1. Обозначим Л = А х + Л 2 + . .. + Л*,;
Л, = A tA k+1, г = 1,2, . . . , k. Тогда
Р{Л1 + Л 2 + . . . + Ak + A h +1} =
= Р{Л + Л*+1} = Р{Л} + Р{Л*+1} - Р{ЛЛ*+1.} =
{далее пользуемся легко проверяемым свойством операций над событиями: для любых событий В, С, D справедливо равенство (В + C)D =
= BD + CD}
= Р { А Х+ Л2 + . . . + Ak} + P{Ak+1} —
—P { A xA k+x + Л2Л^+1+ ... + AkAk+1} =
/Ш
= (E pW.}- E
i\=1
p (a M
\<i\<i2<k
... +(-D‘+'
+
E
Р 1 А Ф М + ...
\<i\<i2<iz<k
E
—P { A i + A 2 + ... + Ak} =
,*+i
= (ЕРГадE eMAH \<i\<i2<h<k
E
/i=l
\<i\<i2<k
. . . + (-!)» '
•£
P{A,,Ah - - - A k } ) ~
\<ii<i2<.-.<ik<k
(S ^ W - Е '’ЙАН
й=1
Е
/>{л.-ЛЛ,>+'
1<й< *2 <*з<&
\< i\< i2 < k
... + (_,)*+!
£
Р{Л,,Л(, . - А } ) =
1ей </2^ ^ ik
,k + \
= (E ptM- E
й=1
1<й<г2Е^
Р {А М +
...+(-i)*+'
j
:
E
^й^й^^зЕ^
W H /J +-
р{л,и,г . . . л , , } ) -
- ( «1=1
E W t t 1}- E mAyVi} +
\< i\< i2 < k
+
E
^>{-^/H«2^*3-^*+l} + • • •
1<«1<*2</з<*
+ ( - 1)‘+1
...
Y.
Р {А ‘А г ■■■A A + l } ) =
1<Й<г2<•••<*£<&
{перегруппи ровы ваем слагаем ы е}
k+ \
У
4
k
= E m ,} -( E р{л,а }+ Е /,{'М*+.}) +
+f E
Г{Л,,Л/2Л/з}+
1 < й < * 2 < г’з<&
P{Ai\Ai2Ak+\}\ +. . .
l< « i< « 2 < ^
. . . + ( ( - 1)й+1/>{Л1Л2 . . . Л , } -(-!)*
P{Ai\Ai2 • • ■Ak-iAk+i}') -
E
l < i i < i 2< - < i k - i < b
- ( - 1 ) * +1
k+ \
= E P{Ai\}~
Й=1
Y
E
P { A hA h . . . A ikA k+l}
Я{Л(1Л,2}+
1^Й<С«2^^Ч_1
+ ... + ( - l ) ‘+l
+ (_l)*+2
Y
E
^>{-^г1Лг2Л/3}+
1^Й <С«2<^^3^^“Ь1
P { A hA i l . . . A k } +
£
l<ii<«2<...<^+i<^+l
P{A,,Ah . . . A , w }.
Последнее равенство означает, что утверждение теоремы выполняется при п = k + 1. Таким образом, теорема доказана методом
математической индукции.
Вернемся теперь к решению задачи. Пусть Л г- — событие, состоящее в том, что i-й посетитель взял свою шляпу, / = 1, 2, . . . , п.
Тогда по классической формуле подсчета вероятности
pr/|.i _ ( N - 1 ) ! _ 1
р Г^ ^ 1 _ (N - 2)! _
Л.)
Р1А
П Л , ЯА , Л
к 1 -- tN т~ ~3)!;V(,V
Р1Л - А ■
1 “ 12 "
1
1 ■2) ..................
- !)f;V
А • ) = ^ ~ т ^ = __________ -__________
(m-r
ЛП
N
{
N
• • Л (ЛГ1}
—,
’
P{j4('jy4»2 • •
Поэтому
Е ЯМ
(=1
=
+ +
+ =1>
'-----------v---------- '
число слагаемых C'n = N
J2
P{AiAj} =
1
_
^
число
+ . .. + Щ Г Г 1 ) = 2!’
v
^
^>9t = ----------iV!
слагаемых CN~
(N—
2)!2!
4
\<i<j< k<N
— v*
число слагаемых
V
ил л
Л
1
с?,=
^-(дг_3)!3!
- (w- ”>' I
4
\<il<i2<...<im <N
! ■I $
I <w~ m>! - 1
1111 v —
число слагаемых CN
Z = i(N—
m)\m\
Y
p {AhAi2 ■■-AiN_{} —
1<4<02<-..<(/ v—
+
s—
+ ■• • + jjj — (jv_ n r
— v----------- /
число слагаемых C ^ ~ l = N
Y
\<i\<i2<---<iN<N
p {AiiA i2 ■■•A l = P {A \A 2 .. . A n } =
Следовательно, по доказанной теореме искомая вероятность того,
что хотя бы один посетитель взял свою шляпу, равна
Р{А\ + А 2 + .. . + Av} = 1 — г Г^зУ — ••• +
Заметим, что выражение 1 —Р{А\ + А 2 + .. . + -А } представляет
собой (N-+ 1) первых членов разложения функции е* в ряд Маклорена при х = —1:
так что при больших N
P { A x + A 2 + . . . + A N} & 1 - е-1 = 0,63212 . . . .
Поскольку ряд для экспоненты сходится достаточно быстро, то
искомая вероятность практически не зависит от N и близка к 2/3.
И. Пусть 30 шаров размещаются по 8 ящикам так, что для каждого шара одинаково возможно попадание в любой ящик. Найти
вероятность размещения, при котором будут 3 пустых ящика,
2 ящика с тремя шарами, 2 ящика с шестью шарами и 1 ящик
с двенадцатью шарами.
Р е ш е н и е . Общее число N способов разместить 30 шаров
по 8 ящикам можно найти по комбинаторному правилу произведения. Перенумеруем все шары и все ящики. Каждому размещению
поставим в соответствие строку из 30 позиций, где в первой позиции будет стоять номер ящика, в котором оказался 1-й шар, во
второй позиции — номер ящика, в котором оказался 2-й шар,
в тридцатой позиции — номер ящика, в котором оказался 30-й
шар. Тогда число N будет равно числу различных строк. Первую
позицию в строке можно заполнить 8-ю способами, вторую — при
заполненной первой — тоже 8 способами, третью — при заполненных двух предыдущих — тоже 8 способами и т. д. Следовательно,
по правилу произведения
N =
8
-8 -
...-8
'------V------'
= 830.
30 раз
Найдем теперь число N благоприятных размещений. Для этого снова применим правило произведения. Каждому благоприятному размещению поставим в соответствие строку из 4 позиций,
где первую позицию будет занимать объект из трех пустых ящиков, вторую позицию — объект из двух ящиков с тремя шарами,
третью позицию — объект из двух ящиков с шестью шарами
и четвертую позицию — объект из одного ящика с двенадцатью
шарами.
Первый объект можно выбрать С | способами; второй объект — после того, как был выбран первый — можно выбрать
С | • С| 0 • С | способами (здесь С | — число способов выбрать 2
ящика из пяти оставшихся; С®0 — число способов выбрать 6
шаров из тридцати оставшихся;
— число способов разместить
шесть выбранных шаров поровну между двумя выбранными ящиками); третий объект — после выбранных первого и второго —
можно выбрать С | • С24 • Cf 2 способами (здесь С | — число способов выбрать 2 ящика из трех оставшихся;
— число способов
выбрать 12 шаров из двадцати четырех оставшихся; С®2 — число
способов разместить 12 выбранных шаров поровну между двумя
выбранными ящиками), после чего четвертый объект может быть
выбран С\ ■С\I способами, т. е. одним способом.
Значит, по правилу произведения
\т
/°3 /^*2/^*6 /^3
— С8
• Ь5О301>6 \U3Lr24L42,
и искомая вероятность Р по классическому определению будет
равна
Р = % = 1(Г8 • 4,0269 . . . .
N
§ 3. Условная вероятность,
формулы полной вероятности и Байеса
Пусть события А и В связаны с одним и тем же экспериментом Е, причем Р{В} > 0. Тогда отношение Р{ А В } /Р { В } называется условной вероятностью события А при условии, что
произошло событие В, и обозначается Р{А \ В}:
Можно предложить следующую мотивировку этого определения.
Под условной вероятностью события А при условии В естественно
понимать долю равновозможных и несовместных исходов, приведших к А, среди тех исходов, которые приводят к В. Пусть
эксперимент Е всегда приводит к одному из N равновозможных
и несовместных исходов, при этом Л/д из этих N исходов приводят
к событию A, N b — к событию В, N ^ B — к событию АВ. Тогда
доля исходов, приведших к А, среди исходов, которые привели
к В, есть
Nab
Nb ’
а эту дробь можно представить как
Na
b
/N
N g /N
_
Р {А В }
Р{В}
'
Событие А называется независимым от В, если Р{А \ В } = Р { А ) .
В этом случае Р{АВ} — Р{ А} Р{В }, откуда при Р{А} > 0 получаем Р{В | А} = Р{В}, т. е. В также независимо от А.
Из определения условной вероятности следует
Р{АВ} = Р{А | В }Р { В } — Р { В \ А } Р { А } ,
т. е. вероятность произведения двух событий равна произведению
вероятности одного из этих событий на условную вероятность
другого при условии, что первое произошло. Это правило иногда
называют теоремой умножения вероятностей. Для независимых событий оно принимает вид
Р{АВ} = Р { А } Р { В } .
Пусть теперь событие А может осуществиться с одним и только одним из п несовместных событий Н\,Н2,
Это условие, в частности, выполняется, если сумма несовместных событий Н\ + #2 + . .. + Нп есть достоверное событие (в этом случае
говорят, что # ь # 2, . . . , # я образуют полную группу событий).
Тогда
А = АН\ + AH<i + . .. + А Н п.
Отсюда в силу несовместности событий, суммируемых в правой
части последнего равенства,
P { A }
=
j^ P { A H i
},
(1)
i= i
или, использовав теорему умножения, получаем
P{A} = ' £ P { A \ H i}P{Hi}.
i=\
Это равенство носит название формулы полной вероятности
Далее, по теореме умножения
Р Щ А } = Р{А | Hi}P{Hi} = P{Hi | А }Р { А } ,
откуда
т
\Л } . Р ! * т
р>,
или, используя формулу полной вероятности, приходим к формуле
Р{Я, 1Л}=
w m w )
.
Y ; p {a ]Hi ) p {Hi )
i= 1
Полученная формула называется формулой Байеса. Ее можно
интерпретировать следующим образом. Пусть известно, что к событию А могут привести события Н\,Н 2 , ■■■,Нп. Событие А произошло, но неизвестно, какое из событий Я ^Я г, • • • >Нп предшествовало этому. Если’найдены условные вероятности Р{Я, |Л},
/ = 1, 2, . . . , «, то естественно предположить, что скорее всего событию А предшествовало то из событий Я,-, которому соответствует большая вероятность Я{Я( 1А}. При такой интерпретации
й) Иногда формулой полной вероятности называют также формулу (1).
события Hi, i = 1, 2, . . . , п, называются гипотезами или причинами, объясняющими факт происхождения А, а сама формула
Байеса называется формулой вероятностей гипотез.
Пример 1. На заводе, изготовляющем болты, на долю 1-й, 2-й
и 3-й машин приходится соответственно 25, 35 и 40 % всех изделий. В их продукции брак составляет соответственно 5, 4 и 2%.
Случайно выбранный из продукции болт оказался дефектным.
Какова вероятность того, что он был изготовлен на 1-й машине?
на 2-й машине? на 3-й машине?
Р е ш е н и е . Введем в рассмотрение следующие события: Я г —
случайно выбранный болт изготовлен на i-й машине, i = 1,2,3;
А — случайно выбранный болт оказался дефектным. Тогда по
условию
Р{НХ} = 0,25;
Р{А \Hi} = 0,05;
/>{Я2} = 0,35;
Р{А | Я 2} = 0,04;
Р{Н3} = 0,4;
Р{А | Я3} = 0,02.
Поскольку несовместные события Я ь Я 2,Я з образуют полную
группу, то по формуле Байеса получаем искомые вероятности:
J2P{A\H,}P{H,)
i= 1
0,05 • 0,25
25
“ 0,05 • 0,25 + 0,04 • 0,35 + 0,02 • 0,4 ~ 69’
, й |л ) = Ж
№
•£,Р{А\Н,}Р{Н,}
p № |A} = ^ M № № L = | .
52Р{А\Н,}Р{Н,}
1=1
Пример 2. Два игрока ведут некоторую игру, состоящую из
отдельных партий, до полного разорения одного из них. Капитал
первого равняется а руб., капитал второго b руб. Вероятность выигрыша каждой партии для первого игрока равна р, а для второго
игрока равна q; р + q = 1 (ничьи отсутствуют). В каждой партии
выигрыш одного игрока (а значит, проигрыш другого) равен 1 руб.
Под разорением игрока понимается момент, когда капитал игрока
становится равным нулю. Найти вероятность разорения каждого
из игроков, если результаты отдельных партий независимы.
Р е ш е н и е . Пусть Рп — вероятность разорения первого игрока, когда он имеет п руб. Тогда искомая вероятность для него
есть Ра', при этом Ра+ь = 0 (если капитал первого игрока а + Ь, то
капитал второго равен 0 , и игра закончится, так что первый игрок
никогда не разорится), P q — 1 (если капитал первого игрока 0, то
факт его разорения свершился).
Пусть событие А —- первый игрок разорился при исходном капитале п; событие Я — первый игрок выиграл очередную партию.
Тогда по формуле полной вероятности
Р{А} = Р{А | Н }Р {Н } + Р{А | Н} Р{Н).
Поскольку
Р{А} = Рп,
Р{Н}=р,
Р{Н} = q,
P { A \ H } = Pn+h
Р { А \ Н } = Рп_ ь
то получаем
Р п — Р П + \ Р “I" Р п —\Я '
Отсюда для любого п — 1,2, . . . , а + b — 1 имеем:
Р„(р + q ) = Рп+\Р + Pn-\q,
q{Pn - Р п - 1) = р(Рп+1 - Рп),
Pn+l - P n = ^ P n - P n-l).
Значит,
откуда
£(/>»+. -« о = E ( f ) V i - » k= 0
k= 0
так что, считая пока q ф р, получаем:
Рп+ 1 - Р
0
= (Pi - 1 ) ^ ч
Р
(2>
2)
<
ИЛИ
Л+1
(«Г-1
Л +i - 1 = (Л - 1)-Ч р/------* - 1
р
Положив здесь я = а + b — 1, получим:
й-\-Ь
( i y _ 1
О—1 = (Р\ —1)— ---------, л - 1
I-'
тогда
1_ Я
р
=
l - -q
' ( Г - 1'
J . m "
'р '
р
11 =
Ур/
( l \ a+b_ ( S }
11 =
\р /
Ур>
" ( Г - ' I - “( Г -1 " ( Г - ‘
е) -еу
( Г - ~ -й Г
Отсюда вероятность разорения первого игрока
а+Ь / п \ а
/ г»\ ^
,
р/
Для случая р = q = 1/2 вероятность разорения найдем, вновь обратившись к равенству (2), из которого получим
Pn+i - 1 = (п + 1)(Л - 1).
При п = а + 6 — 1 имеем
О — 1 = (а + b)(P\ — 1),
Я,-1 = - - к ,
а+0
откуда
Р„ = п (Л - 1) + 1 = 1 -
а+ о
в частности,
р . = 1-
а
6
а + Ь а + Ь'
Таким образом, если капитал а первого игрока значительно
больше капитала b второго игрока, а игроки одинаково искусны
(р = q = 1/ 2), то разорение первого игрока практически невоз™
Ъ
Л
,
можно: Ра =
г ~ 0 при о
а.
a+ b
г
Обратимся теперь к анализу формулы (3). Если через Qt, обозначить вероятность разорения второго игрока при его начальном
капитале Ь, то в силу симметрии задачи
(4)
Предположим, что первый игрок играет лучше, чем второй, т. е.
р > q. Тогда, например, при Ь » а (условно считая Ь ~ оо), получим из (3) и (4):
т. е. умелый игрок даже с малым капиталом может иметь меньше
шансов на разорение, чем игрок с большим капиталом, но менее
умелый.
Задачи
1.
Игральная кость бросается до тех пор, пока не выпадет единица. Известно, что при первом испытании единица не выпала.
Найти вероятность того, что потребуется не менее трех бросаний,
считая первое.
Р е ш е н и е . Пусть Л,- — событие, заключающееся в том, что
при г-м бросании единица не выпала. Тогда искомая вероятность
есть
Р{А\ А 2 А 3 + А 1 А 2 А 3А 4 + ... + А\ Л2 • •. AfcA/i-t-i + ... |^4i} —
_ P{A{A 2Az + А 1А 2А 3А 4 + ... + А\Ач ■■•AkAk+i + • ••} _
Р{М)
Р{А\А 2А 3} + Р{А{А 2АгА4\ + ... + Р{А\Ач .. ■AkAk+\} + ...
Р{М)
2. Пусть вероятность рп того, что в семье ровно п детей, равна
оо
ар п при п > 1, и ро = 1 -
а Рк•Предположим, что все комбиk=\
нации полов п детей равновероятны. Найти вероятность того, что
в семье ровно k > 1 мальчиков.
Р е ш е н и е . Комбинации полов п детей могут быть следующими: п девочек, один мальчик и (п — 1) девочек, . . . , (лг — 1) мальчиков и одна девочка, п мальчиков, т. е. всего (п + 1) комбинаций.
По условию для любого k = 1,2, . . . , п
Р{в семье k мальчиков | в семье п детей} =
fi
1
Далее,
Р{в семье k мальчиков} =
Р {в семье (k + т) детей, из которых k мальчиков} =
=
т— О
оо
= ^ 2 (^Ч в семье k мальчиков | в семье (к + т) детей} х
т—О
х Я{в семье (k Н- т) детей}) =
ОО
.
ОО
= V
1
aDk+m =
2s k + m + 1
р ^
т= 0
т= 0
а Р
О
Р
т -0
ЬЛ-т4-\
о о р
-Е
= - V [хк+т dx =
k+m+ l
р -“ J
т= 0 о
A
м
0
Jk
0
р
а
Р
( х к~ { + Хк ~ 2 + . . . + X + 1 +
^ dx =
О
а ( xk
х к~ 1
х2
= ~ J \ T + r r -l + . . . + j +
.
|
,Д
х= р
x + \n \x-l\j
х= 0
= Q/ i i
\Р
'
1- Р
~
т
3.
Вероятность того, что в справочное бюро в течение одного
часа обратятся k человек, равна \ ke~x/k\ при некотором Л > 0.
Для каждого человека вероятность отказа по ответу на его запрос равна р. Найти вероятность того, что в течение одного часа
ровно 5 человек не получат ответа на свой запрос.
Р е ш е н и е . Введем в рассмотрение следующие события: Нт —
в течение часа в справочное бюро обратились ровно т человек,
т — 0 , 1 , 2 , . . . ; Вт — из числа обратившихся в справочное бюро
в течение часа ровно т человек получили ответ на свой запрос,
т — 0 , 1 , 2 , . . . . Тогда искомая вероятность есть
оо
P{HsBo + HS+\B\ + . . . + Hs+mB m + . . . } — ^ 2 P{Hs+mBm} —
m=0
oo
oo
\s+ m
— ^ 2 P{Bm | Hs+m}P{Hs+m} = ^
m= 0
—A
—p)mps
m= 0
o-A __ ps\ se~x ^
(s + m)\n _ )m s \'vs+me~x
(A(l - p)Y
KS^my.,
' e
= P* e
m\s\ K P> P (s + m)\
s!
^
m\
m=0
m=0
=0
Поскольку
E
x2
3
~
m
^ ==1 + v + 2_ + _ +
= ^ P _
+ + 2! + 3 ! + " ’ ^ ml
m=0
— разложение экспоненты в ряд Маклорена, то
v
2^
т= 0
(А(1~ р))т = е^О-Р)
ml
так что искомая вероятность равна
ps\ se - x дАП_р) _ ps\ se~xP
s!
s!
'
Примечание. При вычислении вероятности Р{В т | Hs+m} была
использована формула Бернулли (см. ниже, §4).
4.
При переливании крови надо учитывать группы крови донора и больного. Человеку, имеющему 4-ю группу крови, можно
перелить кровь любой группы; человеку со 2-й или 3-й группой
крови можно перелить кровь либо той же группы, либо 1-й группы; человеку с 1-й группой крови можно перелить только кровь
1-й группы. Среди населения Si = 33,7 % имеют 1-ю, S2 = 37,5 % —
2-ю, S3 = 20,9% — 3-ю и S4 = 7,9% — 4-ю группу крови. Найти
вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора.
Р е ш е н и е . Пусть событие Я,, i = 1 ,2 ,3 ,4 , состоит в том, что
у случайно взятого больного оказалась кровь г-й группы; событие А — случайно взятому больному можно перелить кровь случайно взятого донора. По формуле полной вероятности
Р {А ) = ^ Р { А \ Н 1}Р{Н,}.
1=1
Здесь P{Hi} = Si, i = 1,2,3,4, где s, = Si/ЮО. Далее, Р{А \ Нх} = si.
Действительно, если больной имеет 1-ю группу крови, то ему можно будет перелить кровь, если случайно взятый донор будет иметь
кровь 1-й группы, а вероятность этого равна sj. Аналогично,
P { A \ H 2} = s 2 + s x,
P { A \ H z} = s 3 + s h
Р { А \ Н 4} = 1.
Таким образом,
Р{А } = sisi + (s 2 + si)s2 + (s3 + si)s3 + s4 =
= sf + s| + S3 + Sl( 52 + S3) + S4 = sf + s| + Sg + 5 i (1
Sj —S4) +54 =
= s | + S3 + Sj + S4O —Si)
- 0,140625 + 0,043681 + 0,337 + 0,052377 = 0,573683.
5. В условиях задачи 4 найти вероятность того, что переливание можно осуществить, если имеются два случайно выбранных
донора.
Р е ш е н и е . Пусть А\ — событие, заключающееся в том, что
кровь можно перелить от первого донора, а Л2 — от второго. Ясно,
что Р{А\} = Р { А 2} = 0,573683 (см. задачу 4). Столь же ясно,
что события А\ и А 2 независимы, ибо выбор первого донора не
меняет статистических свойств генеральной совокупности, из которой затем выбирается и второй донор. Следовательно, искомая
вероятность
Р { А Х+ Л 2} = Р { А Х} + Р {А 2} - Р { А хА 2 } =
Р { А х} + Р { А 2 } - Р { А х} Р { А 2} =
= 1,147366 - 0,3291121 . . . = 0,8182539
6 . В стройотряде 70% первокурсников и 30% студентов второго курса. Среди первокурсников 10% девушек, а среди студентов второго курса — 5 % девушек. Все девушки по очереди дежурят на кухне. Найти вероятность того, что в случайно выбранный
день на кухне дежурит первокурсница.
Р е ш е н и е . Пусть N — общее число студентов в стройотряде.
Тогда среди них 0,7N первокурсников и 0,3,/V второкурсников.
В свою очередь, девушек среди первокурсников 0,1 • 0,7N, а среди
второкурсников 0,05 • 0,3/V. Таким образом, в стройотряде всего
0,1 • 0,7N + 0,05 • 0,3,/V девушек, из которых 0,1 • 0 ,7N первокурсниц. Следовательно, искомая вероятность равна
0,1 • 0,7N
_
0,07
_ 14
0,1 • 0 J N + 0,05 • 0,3N ~ 0,07 + 0,015 - 17'
7. Отдел технического контроля (ОТК) проводит сортировку
приборов, выпускаемых заводом. Каждый прибор независимо от
остальных имеет дефект с вероятностью р. При проверке в ОТК
наличие дефектов обнаруживается с вероятностью а , причем с вероятностью /? исправный прибор при проверке забраковывается.
Найти вероятность qo того, что незабракованный прибор имеет
дефекты, и вероятность q\ того, что забракованный прибор имеет
дефекты.
Р е ш е н и е . Пусть событие А состоит в том, что прибор имеет
дефект, а событие В — в том, что ОТК не забраковал прибор.
Тогда qo = Р{А \ В}, так что
__Р{АВ}_
Р{В\А}Р{А}
(1 - а ) р
_
Яо ~ Р{В} ~ Р { В \ А } Р { А } + Р { В \ А } Р { А } ~ ( 1 - а ) р + ( 1 - / ? ) ( 1 - р ) '
Далее, поскольку q\ = Р{А \ В}, то
_Р{АВ} _
qi ~
Р (В }
Р(В\А}Р{А}
_
ар
~ Р (В | А } Р { А } + Р ( В | А } Р { А } ~ а р + Р ( \ - р ) '
8 . Число отечественных автомобилей превышает число иномарок в 1,5 раза. При проведении технического обслуживания
(ТО) нештатные ситуации с отечественными автомобилями возникают в 2 раза чаще, чем с иномарками. При проведении ТО
с неким автомобилем возникла нештатная ситуация. Какова вероятность, что это отечественный автомобиль?
Р е ш е н и е . Пусть событие А — при проведении ТО автомобиля возникла нештатная ситуация; Н\ — ТО проводится для
отечественного автомобиля, #2 — ТО проводится для иномарки.
Тогда искомая вероятность есть условная вероятность
Р[н М 1
1 11
1
р { А \ н 1} р т
Р { А \ Н 1} Р { Н 1} + Р { А \ Н 2} Р{ Н2}'
Пусть т — число отечественных автомобилей, N — общее число
автомобилей. Тогда
/>{//,} = ^ ,
Р{Н2} = !L = ± .
По условию т = 1,5(АГ—т), откуда Р{Н{\ = 1,5(1 —Р{Н\}), или
Р{Н\} = 0,6, так что Р{Н2} = 0,4. Далее, по условию
Р { Л \ Н 1} __
Р { А | Я 2}
Следовательно,
^ ' л>= ж
р
= 0-75-
9. При рентгеновском обследовании вероятность обнаружить
заболевание туберкулезом у больного туберкулезом равна 1 —/?.
Вероятность принять здорового человека за больного равна а .
Известно, что доля больных туберкулезом по отношению ко всему
населению равна 7 . Найти вероятность того, что признанный при
обследовании больным человек на самом деле здоров.
Р е ш е н и е . Пусть событие Н\ — обследуемый человек здоров,
#2 — обследуемый человек болен, А — обследование показало, что
человек болен. Тогда искомая вероятность есть условная вероятность
рШ М 1_
Р { А \ Н 1} Р { Н 1}
_
а -( 1- 7)
1 11 } P{A\H i}P{Hl} + P{A\H 2 }P{H2} се • (1 —7) + (1 —/3) • 7
10. В 1-й урне содержатся 10 шаров, из них 8 белых; во 2-й урне — 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли
по одному шару, а затем из этих двух шаров случайным образом
выбрали один. Найти вероятность того, что выбран белый шар.
Р е ш е н и е . Пусть событие А — выбран белый шар, так что
Р{А} — искомая вероятность. Пусть событие Hi — из 1-й и 2-й урн
выбраны белые шары, Я2 — их 1-й и 2-й урн выбраны не белые
шары, Яз — из одной урны выбран белый шар, а из другой — не
белый. Тогда
Р ш г - А Л
р / я г - 1 2® - л
* 4
10 20
100’
{ 2*
10 20
100’
Г>{йз} = 1 - Я { Я 1} - Р { Я 2} = 1 - А = ^ .
По формуле полной вероятности
Р{А} = Р{А | Hi }P {H x} + Р{А | Н 2 }Р{Н2} + Р{А | Я3}Р{Я3} =
16
„ 16
1 68
§ 4 . Последовательность независимых испытаний
Пусть некоторый эксперимент Е повторяется п раз. Будем интересоваться определенным событием А, связанным с Е. Пусть
Р{А}=р,
P{A} = l - p = q.
Обозначим через Pn(k) вероятность того, что в серии из п испытаний событие А произошло ровно k раз, где k — любое целое неотрицательное число. Будем считать, что наступление или
ненаступление события А в испытании происходит независимо
от других испытаний серии. Тогда вероятность того, что событие А наступит в k определенных испытаниях, а в остальных
(п — k ) испытаниях не наступит, равна pkqn~k. Значит, по теореме
сложения вероятностей искомую вероятность Pn(k) можно найти
как произведение pkqn~k на число различных способов сочетания
k появлений события А и (п — k) непоявлений среди п испытаний.
Так как число таких способов есть Ckn, то
Pn(k) = Cknpkqn- k.
Полученная формула носит название формулы Бернулли, а описанная схема независимых испытаний — схемы Бернулли.
Введем в рассмотрение функцию
■ф(х) = - = е ~ х2/ 2.
л/27г
.
Оказывается, что при больших п имеет место приближенное
равенство
р "т
к
~ ш т
-
k-np „
где х = —щ = . Точный результат приводится ниже.
Теорема 1 (локальная теорема Муавра-Лапласа). Если п —>оо,
k ->ос и \k — пр\ изменяется в интервале от 0 до Кп, где Кп —
любая неотрицательная функция от п, такая, что К \ / п 2 —> О,
то равномерно по \k — пр\
Pn(k)
lim
ti—►оо ф(х)/ y/npq
= 1,
т. е. для любого е > 0 и достаточно больших п
1 - £ < 4м>(x)/^npq
w(% = < 1 + е Эту теорему иногда называют локальной теоремой МуавраЛапласа.
Обозначим через Pn{k\ < & < &2) вероятность того, что в серии из п независимых испытаний Бернулли событие А появилось
какое-либо число раз из промежутка [6ь&2]. Тогда по теореме
сложения вероятностей несовместных событий
k=k2
Pn(k 1 < k < k2) = £ Pn(k).
k=kl
Используя теорему 1, можно получить приближение для этой вероятности. А именно, имеет место следующая теорема М уавраЛапласа (в отличие от теоремы 1 ее называют также интегральной теоремой Муавра-Лапласа).
Теорема 2 (интегральная теорема Муавра-Лапласа). Для фиксированных Z \ и Z 2
^ lim Р„(пр + zx^/npq < k < n p + Z2 yjnpq) = Ф(г2) - Ф(21),
где
X
X
Ф(х) = [ ф(t) dt = - у = [ e ~ f2/ 2 dt.
J
—00
v
27T
j
—00
Наконец, сформулируем еще один предельный результат, известный как теорема Пуассона.
Теорема 3 (теорема Пуассона). Если р —>0 при п —> оо, то
p n(k) - ^ е ~ х - О,
где А = пр.
Этот результат позволяет при больших п и малых р использовать приближенную формулу
/>„<*, и
называемую приближением Пуассона.
Задачи
1. В семье 10 детей. Считая вероятности рождения мальчика
и девочки равными 1/ 2, найти вероятность того, что в семье:
а) 5 мальчиков и 5 девочек; б) число мальчиков не менее 3 и не
более 8.
Р е ш е н и е . Ясно, что для решения задачи можно привлечь
схему Бернулли при п = 10, р = 1/2. Если под событием А (или
успехом, по общепринятой для схемы Бернулли терминологии)
понимать рождение мальчика, то
Р{в семье 5 мальчиков и 5 девочек} = Яю(5) =
=
- J 2!_ J _ - 63 ■
“ 5!5! ' 210 ~ 256’
k=8
Р{в семье мальчиков от 3 до 8} = ^ P\o(k) =
k= 3
= v r * n V ' V 0- * » . ^
^
10 \ 2/ \ 2 /
1024’
k= 3
2. Найти наиболее вероятное число успехов в серии из п испытаний Бернулли с вероятностью успеха р в одном испытании.
Р е ш е н и е . Речь идет о нахождении такого k в формуле
Бернулли
Pn(k) = Cknpkqn- k
при заданных п и р = 1 —q, при котором вероятность Pn(k) принимает наибольшее значение. С этой целью вычислим отношение
п'
pk+iqn-k-i
Pn(k + 1) _ (k + !)!(« —fe —1)!
____
Pn(k)
n!
k k
k\(n-k)\p q
_
k\(n —k)\
p_ n -k p
~ (k + \ ) \ ( n - k - \ ) \ ' q ~ k + l ' q'
Следовательно,
Pn(k + 1) > Pn(k) <*=>( n — k)p > (k + l ) q
Pn(k + 1) = Pn(k) -ФФ- k = np - q\
Pn(k -I-1) < Pn{k) & k > n p - q.
k < np — q;
Это наблюдение показывает, что вероятность Pn(k) с увеличением k сначала возрастает, затем достигает максимума и далее
убывает. При этом если пр — q является целым числом, то максимальное значение вероятность Pn(k) принимает для двух значений k\ пр — q и пр — q + 1 = пр + р. Если же пр - q не является целым числом, то максимального значения вероятности Pn{k)
достигает при k, равном наименьшему целому числу, большему
пр — q. Суммируя все сказанное, можно написать
пр - q < &Н.В. < пр + р,
(1)
где &н.в. — значение k, при котором Pn(k) принимает наибольшее
значение; при этом если пр — q — целое, то условию (1) удовлетворяют сразу два целых значения £ н.в.> которые дают одинаковое
значение Pn(k), т. е. в этом случае получаем сразу два наиболее
вероятных значения k : kH_B, = пр — q и kH,B. = пр + р.
3.
В институте обучаются 730 студентов. Вероятность того,
что день рождения наудачу взятого студента приходится на определенный день года, равна 1/365 для каждого из 365 дней. Найти
наиболее вероятное число студентов, родившихся 1 января.
Р е ш е н и е . Будем перебирать по очереди всех студентов,
и если очередной студент родился 1 января, то это событие будем
считать успехом. Тогда искомое число — это наиболее вероятное
число &н.в. успехов в серии из п = 730 испытаний Бернулли с вероятностью успеха р = 1/365 в одном испытании. Следовательно,
можно воспользоваться результатами задачи 2:
пр - q < kH.B. < пр + р,
откуда £н.в. = 2.
4.
В условиях задачи 3 найти вероятность того, что найдутся
по крайней мере три студента, родившихся 1 января.
Р е ш е н и е . Искомая вероятность
Р 7зо(3 < k < 730) = 1 - Р 7зо(0 < k < 2 ) =
= 1 - -Р7зо(0) ~ Л'ЗоО) - -Р7зо (2).
Используя приближение Пуассона
где А — пр, найдем
Л'зо(О) = е~2,
Я 730 О )
= 2е-2 ,
Я73о(2) = 2е~2,
так что искомая вероятность равна
1 - 5е-2 « 0,32.
5.
В условиях задачи 3 найти вероятность того, что найдутся
по крайней мере три студента, родившихся в один день (все равно
какой)?
Р е ш е н и е . Для решения этой задачи получим следующее
обобщение формулы Бернулли. Пусть в каждом из п испытаний
может произойти одно и только одно из k событий A i , A 2 , . .. , Л*,
испытания независимы и в каждом из них событие Л* происходит
с вероятностью р Тогда вероятность того, что в п независимых
испытаниях появятся т\ событий А\, m2 событий А 2, . . . ,
событий Ak, равна
Pn(mh m 2 , . . . , m k) = — — ^ ----- -,рТрТ • • -р Г где т\ + m 2 +'.. . + mk = п. Действительно, вероятность того, что
в mi определенных испытаниях произошло событие Л ь в т г определенных испытаниях — событие Лг, ..., в /га*, определенных испытаниях — событие Ak, равна p f ’p™2 • • -Р**- ^ Р и этом из п ис*
пытаний набор т\ можно выбрать С™1 способами, из оставшихся
(п —т\) испытаний набор m 2 можно выбрать C%im способами,
из оставшихся (п — т\ — m 2 ) испытаний набор m3 можно выбрать
числом С ™
способами, и т. д. Общее число вариантов, каждый из которых будет иметь вероятность p f ‘р^ 2 ■■■Р™к>п0 правилу произведения будет равно
/^гп\/^гп2
WW3
г> Щ -\
^ п —т\ ^ п —т \—т 2 ' * * ^ п —rri\—т^ —
т ^ -2
пт ъ
п —т \ —m 2 —
mk - \
п\
(п —ГП\)\
(п —ТП\ —m2)!
m i ! ( n — m i) !
m 2 ! ( я — m i — m 2)!
m 3 ! (гг — m \ — m 2 — m 3 )!
(п - mi - ... - mk- 2)\
x
(n - mi - ... - mk~2 - mk- 1)!
mkl0!
n\
mi!m2! .. •m^!’
что и доказывает приведенную выше обобщенную формулу Бернулли.
Вернемся к решению задачи 5. Пусть В — событие, вероятность которого нужно определить. Тогда противоположное событие В будет означать, что в каждый из 365 дней ровно у двух
студентов день рождения. Пусть событие Л*, k = 1,2, . . . , 365, состоит в том, что у случайно выбранного студента день рождения
в k-Pi день. Тогда pk = P{Ak} = 1/365 для любого k = 1, 2 , . . . , 365.
Вероятность Р{В} есть вероятность того, что в серии из п = 730
испытаний (испытание — выбор очередного студента) каждое из
событий Ak, £ = 1 , 2 , . . . , 365, произойдет ровно два раза. Значит,
по обобщенной формуле Бернулли
Используя известную приближенную формулу Стирлинга
п\ к, V 2 irnnne ” ,
получаем для Я{5} следующее приближенное значение:
-н, _ л /2 ^ 7 3 0 • 730730 • е- 730
' 1~
2365 • З65730
Ясно, что это ничтожно малое число. Следовательно, искомая
вероятность Р{В} = 1 —Р{В} практически равна единице.
6.
Предполагая все комбинации полов детей равновероятными, определить, какую долю семей с шестью детьми будут составлять семьи с тремя мальчиками и тремя девочками.
Р е ш е н и е . Рассматривая рождение ребенка как испытание
(по терминологии схемы Бернулли), а рождение мальчика как
успех, найдем вероятность того, что в семье с шестью детьми
ровно три мальчика:
т. е. в среднем на каждые 16 семей с шестью детьми будет 5 семей,
где мальчиков и девочек поровну.
7.
Найти вероятность того, что среди 13 карт, наугад выбранных из колоды в 52 карты, имеются ровно две карты красной
масти. Сравнить ее с соответствующей вероятностью для испытаний Бернулли (т. е. когда выбранная карта опять возвращается
в колоду) с р = 1/ 2.
Р е ш е н и е . По классической формуле (т.е. как отношение
числа благоприятных исходов к общему числу исходов) искомая
вероятность равна
26!
26!
_ Cl6 • С&_ 21241 11! 15! _ 5 ' 13 • 13 • 19 _ n пПопс
Р~
с£
~
52!
“ 41-43-47-49 ” ’
13! 39!
Если же считать, что выбранная карта опять возвращается
в колоду, топрименима формула Бернулли с р = 1/2 и
Л з ( 2) =
= 2Ш! ' !>TJ = ^ i r = 0 .0 ° 952 " •
8.
Какова вероятность того, что дни рождения шести человек
приходятся ровно на два месяца, оставляя десять месяцев свободными? Предполагаются независимость и равновероятность всех
месяцев.
Р е ш е н и е . Число способов выбрать два месяца из двенадцати равно
-.2 _ 12!
66 .
' 12
2! 10!
Обозначим через Р вероятность того, что дни рождения шести
человек приходятся ровно на два определенных месяца, оставляя
десять месяцев свободными. Тогда, очевидно, искомая вероятность равна 66Р.
Найдем Р. Пусть Pi — вероятность того, что все дни рождения
приходятся на 1-й месяц; Рг — вероятность того, что все дни
рождения приходятся на 2-й месяц; Р \2 — вероятность того, что
все дни рождения покрываются указанными месяцами. Тогда
Р \2 — Р + Р \ + Рг,
откуда
P = Pl2 - P l - P 2.
По формуле Бернулли
у
^ 6Ш6(§)Ч)6
'•-(ИЧйЧй'О -й-!-■«)■•
Следовательно,
и искомая вероятность
66Р
31-66
31-11
= ^ = ^
= 0,00137....
32 • 6'
9.
Книга в 250 страниц содержит 500 опечаток. Оценить вероятность того, что на заданной странице не менее трех опечаток.
Р е ш е н и е . Будем считать, что любая опечатка с одинаковой вероятностью может оказаться на любой из страниц. Тогда
вероятность того, что i-я опечатка окажется на заданной странице, равна р = 1/250, / = 1 , 2 , . . . , 500. Обнаружение очередной
опечатки по терминологии схемы Бернулли будем называть испытанием, а попадание этой опечатки на заданную страницу —
успехом. Тогда число испытаний п = 500 и искомая вероятность
Рьоо(3 < k < 500) = 1 - Р 5оо(0) - PsooO) - Л>оо(2),
где по формуле Бернулли
Люо(0) = С5°00р°(1 - р ) 500,
Р 5оо(1) = С>ооР1(1 - Р ) 4">
Р 50о(2) = С |00р2( 1 - р ) 498.
Используя приближение Пуассона, найдем (обозначив А = «р = 2)
Р 5оо(0) « ^ е ~ х = е ~ 2 = 0,135 . . . ,
Р 5оо(1) «
= 2 е~'г = 0,270 . .. ,
Рьo o ( 2 ) « f e - A = 2в- 2 = 0 , 2 7 0 . . . ,
так что искомая вероятность
Рб00(3 < k < 500) и 1 - 0,135 - 0,270 - 0,270 = 0,325.
10.
Некий математик носит с собой две коробки спичек. Каждый раз, когда он хочет использовать спичку, он выбирает наугад
одну из коробок. Найти вероятность того, что когда математик
впервые вынет пустую коробку, в другой коробке окажется г спичек (г = 0,1,2, . .. ,N\ N — начальное число спичек в каждой из
коробок).
Р е ш е н и е . Присвоим коробкам номера 1 и 2. Пусть событие А состоит в том, что 1-я коробка оказалась пустой, а во 2-й
в этот момент было г спичек; событие В — 2-я коробка оказалась
пустой, а в 1-й в этот момент было г спичек. Тогда искомая вероятность равна
Р{А + В} = Р{А} + Р{В}.
Из симметрии ясно, что Р{А} = Р{В}. Найдем, например, Р{А}.
Пользуясь терминологией схемы Бернулли, выбор коробки будем
называть испытанием, причем под успехом (вероятность которого
в данном случае равна 1/ 2) будем понимать выбор 1-й коробки.
Тогда
в серии из п = N + (N —г) испытаний было
ровно N успехов, причем (п + 1)-е испытание
тоже было успехом
{
(п + 1)-е испытание 1
было успехом
(
х р \ в серии из n = N -f (N —г) испытаний
было ровно N успехов
Ч 'сМ :0 Ш
1
/ 1 \ N / 1 \ N —г
Следовательно, искомая вероятность равна
nN
( \ \ 2N~r _ (2 N - r ) l ( \ \ 2N~r
2N~r \ 2 j
N\(N-r)\\2J
/ 1 \ 2А^—гЧ-1
•
§ 5. Случайные величины
и функции распределения
Пусть (Q, Т , Р) — вероятностное пространство, связанное
с экспериментом Е (см. §2). Пусть X = Х(ш) — конечная вещественная функция, определенная для всех элементарных событий и>, составляющих множество О = {о;}. Говорят, что функция X измерима, и называют ее случайной величиной, если
для любого действительного х множество всех ш, для которых
Х{и>) < х, принадлежит сг-алгебре Т .
Упрощенно случайную величину можно трактовать как некую
количественную характеристику, связанную с экспериментом Е,
значение которой непредсказуемым (т. е. случайным) образом
меняется от эксперимента к эксперименту. При этом измеримость
означает, что для любого действительного числа х определена вероятность Р{Х < х}. Эта вероятность представляет собой
неубывающую функцию F(x) = Р{Х < х} вещественного переменного х, которая носит название функции распределения (ф.р.)
случайной величины X. Можно показать, что F(x) непрерывна
слева, lim F(x) = 0, lim F(x) = 1.
х—>—оо
х—►Н-оо
Пусть х \ , х 2 — два произвольных действительных числа, удовлетворяющих неравенству х\ < х 2. Тогда
Р{х 1 < Х < х 2} =
F { x 2)
- F(x i),
(1)
т. е. вероятность попадания случайной величины в промежуток
(точнее, в полуинтервал с открытым правым концом) равна разности значений функции распределения на концах промежутка.
Действительно, так как
{Я < х 2} = {X < х\} + {х\ < X < х 2},
и события {X < х\} п {xi < X < х 2} несовместны, то по теореме
сложения вероятностей
Р{Х < х 2} = Р { Х < xi} + Р{х 1 < X < х 2},
откуда и следует равенство (1). Это равенство широко используется в приложениях, когда для случайной величины с известной
функцией распределения требуется найти вероятность ее попадания в заданный промежуток.
Случайная величина X называется дискретной, если множество ее возможных значений конечно или счетно: Х\,Х 2 , . . . .
В этом случае таблицу
Значение случайной величины
Х\
*2
Вероятность
Р\
Р2
где pi = Р{Х = х*}, называют законом распределения случайной
величины. При этом, очевидно,
P{(X =
X l)
+ (X =
X 2 ) + . . . } = ' £ i P i = I-
Последнее равенство называется условием нормировки.
Приведем примеры дискретных распределений.
1.
Биномиальное распределение. Пусть X — случайная величина, представляющая собой число успехов в серии п независимых испытаний с вероятностью успеха р в каждом испытании.
Тогда соответствующий закон распределения называется биномиальным и характеризуется таблицей
0
1
2
(1 - р ) п О С ! - а )"-' С У ( 1 - р Г ~ 2
------------------где вероятность Р \ Х =
ле Бернулли (см. §4):
k
п
Cknpk(l - p)n~k
Рп
вычисляется по форму-
P{X = k} = C « p * ( \ - p )\ n —k
2.
Ггометрическое распределение. Пусть X — случайная величина, представляющая собой число испытаний до первого успеха в серии независимых испытаний с вероятностью успеха р в каждом испытании. Тогда таблица возможных значений случайной
величины и их вероятностей имеет вид
1
2
Р 0 -Р)Р
3
О ~Р?Р
k
(1 - p f - ' p
Распределение, определяемое этой таблицей, называется геометрическим.
3.
Распределение Пуассона. Так называется распределение
дискретной случайной величины, определяемое таблицей
О
„-А
1
-А
Хе - А
k\
где Л > 0 — параметр распределения, а вероятности Р{ Х = k}, где
k = 0 ,1 ,2, . . . , вычисляются по формуле Пуассона (см. §4)
р { х = k} = £ е- х:
Как видно, биномиальное распределение — это распределение
дискретной случайной величины с конечным числом возможных
значений (или, как иногда говорят, с конечным спектром), характеризуемое при этом двумя параметрами: п и р . Геометрическое распределение и распределение Пуассона — распределения дискретной случайной величины с бесконечным (счетным)
числом возможных значений (как говорят, с бесконечным спектром), характеризуемые одним параметром: параметром р в случае геометрического распределения и параметром Л в случае распределения Пуассона.
Наряду с дискретными случайными величинами будем рассматривать класс случайных величин, для которых существует
неотрицательная функция f(x), удовлетворяющая при любом х
равенству
F(x) =
f{t) dt.
Случайные величины, обладающие этим свойством, называются непрерывными, а функция f(x) называется плотностью распределения соответствующей случайной величины. Из определения Цх) и свойств ранее введенной функции распределения Fix)
следует, что
+00
fix) dx = 1;
(2 )
При Л Ю б ы Х Х \ И Х 2 (X i < Х 2 )
Х2
X,
Равенство (2) — аналог дискретного условия нормировки в непрерывном случае. Отметим также, что если F(x) дифференцируема, то
F'{x)=f(x).
Если /(х) ограничена в окрестности точки хо, то из равенства (3) легко выводится, что Р{Х = х о} — 0, т. е. если непрерывная случайная величина имеет ограниченную плотность распределения, то вероятность принятия этой случайной величиной
любого заранее заданного значения равна нулю. В частности,
для таких случайных величин вероятность попадания в заданный промежуток вещественной оси не зависит от того, какой это
промежуток — открытый или замкнутый. Отметим также, что
если /(х) непрерывна в точке хо, то с точностью до бесконечно
малых высших порядков
Р {х 0 < X < хо + Ах} « /(хо) Ах,
т.е. при малых Ах значение /(хо) приближенно равно вероятности, приходящейся на единицу длины рассматриваемого промежутка от хо до хо + Ах. Этим обстоятельством отчасти объясняется появление слова «плотность» в названии функции /(х).
Приведем примеры непрерывных случайных величин.
1. Случайная величина, определяемая плотностью распределения
/(*) = {
(О,
x £ i a ’bi
х£[а,Ь\.
Здесь а,Ь — параметры распределения, а < Ь. Такое распределение называется равномерным на отрезке [а,Ь] . Название распределения оправдано тем, что вероятность попадания в любой промежуток [x\,x<z\ С [а, Ь\ равна ^ т . е .
определяется только
длиной Х2 —х\ промежутка [х\,Х2 ] и не зависит от его расположения на отрезке [а, Ь\. При этом вероятность попадания в любой
промежуток, лежащий вне отрезка [а,Ь], равна нулю.
Функция распределения случайной величины будет иметь вид
2. Случайная величина, определяемая плотностью распределения
I0'
х < О,
1[Хе
Ае_Л*,
^
х > 0;
А — параметр распределения, А > 0. В этом случае говорят, что
случайная величина распределена по показательному закону.
Функция распределения такой случайной величины есть
X
: : ° 0;
3. Случайная величина, определяемая плотностью распределения
/(*) = _L_e-(*-*)2/(2т2)>
у 2 жа
где а, сг — параметры распределения, причем а > 0. Такое распределение называется нормальным, или гауссовским. Соответствующая функция распределения имеет вид
F(x)=
X
J f(i)dt=
Х
|
at =
{x—a)/(T
где
Чу)
—оо
-.e -<2/ 2 dt
л/2тг
табулированная специальная функция, уже встречавшаяся в §4.
Задачи
1. Случайная величина X задана законом распределения
Х\
*2
*3
Х4
Р\
Р2
Рз
Ра
Найти функцию распределения F{x) этой случайной величины
и построить ее график.
Р е ш е н и е . Исходя непосредственно из определения для F(x),
находим
При X < Х{,
при
Р\
Х\ < X < х%
При Х<1 < X < Хз,
Н х ) = < р\ + р 2
Р\ + Р 2 + Р З
.Р1+ Р 2 + Р З + Р 4
при
Хз < X < х 4,
при
Х > Х 4.
В силу условия нормировки р! + р 2 + рз + Р4 = 1, так что F(x) = 1
при х > х 4. График изображен на рис. 4.
kF(x)
о
1
о
Pi + /7 2 + Р З
о
Р\ +Р2
р\ -<>
ОХ\
X
Х2
*3
Х4
Рис. 4
Анализируя решение этой задачи, нетрудно сообразить, что
функция распределения любой дискретной случайной величины
есть разрывная ступенчатая функция («лесенка»), скачки которой происходят в точках, соответствующих возможным значениям случайной величины, причем величины скачков равны вероятностям этих значений. При этом сумма всех скачков функции F(x) равна 1. По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними
число скачков становится больше, а сами скачки — меньше; ступенчатая кривая становится более плавной.
2. Плотность распределения случайной величины X задана
формулой:
Найти постоянную С и функцию распределения случайной величины X.
Р е ш е н и е . В силу условия нормировки должно выполняться
соотношение
+00
f{t) dt — 1,
—ОО
так что применительно к нашему случаю получаем
J
+оо
J
Ct~V 2 d t = 1,
1
откуда
С = 2Таким образом,
№ =
/ < l.
Функция распределения случайной величины X будет равна
О,
х < 1,
.
х > 1.
F{x)
3.
Пусть дана случайная величина Y = \/Х , где X — случайная величина, определенная в задаче 2. Найти плотность распределения fy{t) величины Y и вероятность Р{0,1 < У < 0,2}.
Р е ш е н и е . Найдем сначала функцию распределения Fy(y)
случайной величины Y. Имеем
Ру(у) = Р { У < у } = р { ± < у } .
Из задачи 2 следует, что в промежуток (—оо, 1) случайная величина X попадает с нулевой вероятностью. Следовательно, случайная величина l / Х с нулевой вероятностью попадает в объединение промежутков (—оо, 0) U (1, +оо). Поэтому
р { ^ < г/} = 0
при
у < 0,
р { ^ < г / } = 1 при
При 0 < у < 1
У>
\У>
у > 1.
Итак,
FY(y)
0,
у < О,
у/У,
о < у < 1,
1,
у > 1-
Следовательно,
ГО,
У<
о,
1
О < у < 1,
2^ ’
10,
у > 1.
При этом искомая вероятность
0,2
Р{0,1 < Y < 0,2} = | Ш
dy = F y {0,2) - F y(0,l)
0,1
4.
Построить графически и выразить аналитически функцию
распределения случайной величины X, которая с вероятностями,
равными 1/4, принимает значения —1 и 1 и имеет постоянную
плотность распределения в промежутке (—1/ 2, 1/ 2).
Р е ш е н и е . Поскольку значения —1 и 1 принимаются с вероятностью 1/4 каждое, то в промежуток (—1/2,1/2) случайная величина X попадает с вероятностью 1 - (1/4 + 1/4) = 1/2. Если / —
постоянная плотность распределения в промежутке (—1/ 2, 1/ 2),
то
1/2
/ dx
-
1
2’
1/2
откуда / = 1/2. Пусть F(x) — функция распределения случайной
величины X. Тогда при х < —1
F(x) = Р{ Х < х} = 0;
при —1/2 < х < 1/2
F(x) = Р { Х < х } =
р
{ ( Х = -1 ) + ( х е ( - 5 . * ) ) } =
1
г *■j
J fd x- 4
" 4+
-
1
1/
+
2
1А
1
1
\ X + 2 j “ 2 + 2Х;
1 /2
при 1/2 < х < 1
FW = P { X < x } = p { ( X = - l ) + ( ^ e ( - i , I ) ) } = I + I = |;
при X > 1
F(x) = Р { Х < х } = 1.
График функции F(x) изображен на рис. 5.
Рис. 5
5.
Показать, что если случайная величина X имеет непрерывную строго возрастающую функцию распределения Fx (x), то случайная величина Y = Fx(X) равномерно распределена на отрезке [0 , 1].
Р е ш е н и е . Обозначим через Fy{y) функцию распределения
случайной величины Y. Заметим, что область возможных значений случайной величины Y ограничена отрезком [0,1]. Поэтому,
очевидно,
[ 1,
У > 1-
Пусть теперь у € (0,1]. По определению
Fy(y) = P { Y < у} = P{Fx (X) < у}.
Поскольку Fx(x) строго возрастает и непрерывна, то существует
непрерывная обратная функция F% 1 и неравенство Fx(X) < у эквивалентно неравенству X < F% 1(у). Следовательно,
P{Fx (X) < у } = Р { Х < F x \ y ) } = Fx (F-'(y)) = У■
Таким образом,
Г о,
у <
0;
U
0 <
у
ру(у) = \у>
^
у > 1.
А это и есть функция распределения случайной величины, равномерно распределенной на отрезке [0 , 1].
6.
Рассмотрим последовательность однотипных событий, происходящих в случайные моменты времени. Например, это могут
быть звонки, поступающие на телефонную станцию; неисправности, возникающие в процессе работы сложного технического
устройства; дорожно-транспортные происшествия, происходящие
в заданном регионе; и т. п. Обозначим через K(t) случайную величину — число таких событий, происходящих в промежутке времени (0, f]. Говорят, что упомянутая последовательность событий
образует простейший пуассоновский поток е интенсивностью Л,
если случайная величина K(t) при любом / > 0 имеет распределение Пуассона с параметром А/, т. е. если
P{K(t) = т } = (Xt)2
Х‘,
т = 0,1,2,....
Пусть сбои в работе компьютера образуют простейший пуассоновский поток с интенсивностью Л. Каждый сбой с вероятностью р приводит к ошибке независимо от других сбоев. Найти
функцию распределения случайной величины Z — числа ошибок
в единицу времени (т. е. при t = 1).
Р е ш е н и е . Пусть F(Z) — искомая функция распределения.
Поскольку Z может принимать только целые неотрицательные
значения, то
(здесь [г] означает целую часть числа г), т. е. достаточно находить значения F(k), где k = 1,2, — Имеем
F(k) = P { Z < k } = P{(Z = 0) + (Z = 1) + . . . + (Z = k - 1)} =
k -\
= J 2 p i z = m}.
m=0
Далее,
OO
\
s
P \Z — m\—
P ! ПР0И30ШЛИ (m + 0 сбоев и из I _____
^ —
~ Z-s ]^них ровно
m привели к ошибке J
°° р Г ровно т сбоев
произошли 1 р f произошли
1 _
(^привели к ошибке (т + /) сбоевJ
| (т + 1)сбоевJ
Е
/=0
= У
' с т рт( 1 p)l Xm+le~x - V
2 ^ L m+lP I 1 P)
+
iL
/=0
/=0
+
m\n
p)l Xm+‘e~x -
p *
(/» + /)!
_ Y ' P*(l - p)lXm+le~x _ Xme~x m A
~
m ill
~
m\
P
1=0
A'(l - p )1
l\
1=0
Заметив, что последняя сумма представляет разложение в ряд
экспоненты ех(-1~р\ получаем
P {Z = т} = * - ! _ р”е*а-Р> = Л р е
L
J
m!
яг!
Значит,
k-\
Fik) = £ P {Z = m i = ^
/я=0
m=0
\m nm -A p
=
= e~Xp( l +
Ap + (A p)2
1!
2!
+
(Ap),* -l
(* —1)! У
7.
Пусть случайная величина X имеет плотность распределения f{x). Найти плотность распределения g(y) случайной величины Y = а Х + /3, где а,(3 — заданные постоянные, а ф 0.
Р е ш е н и е . Обозначим через F(x) функцию распределения
случайной величины X, а через G(y) функцию распределения случайной величины Y. Тогда при а > 0
G(y) — P { Y < у} = Р { а Х + (3 < у } = р { х < у- ^ - } =
так что
^ - ^ dy- М Чdy г ) - У ( Ч г ) Если же а < 0, то
G(y) = P { Y < y } = Р { а Х + ( 3 < у } =
= р |х >
= 1 - р | х < у- ^
\ = 1
Таким образом, при любом значении а Ф О
ё(У) = ^\а\Л \ ^ ~a ) J8. Случайная величина X имеет показательное распределение
с параметром а , т. е. ее функция распределения
F(x) = Р { Х < х} =
10,
в~аХ’ Х ^ ° о
х < 0.
Найти плотность распределения случайной величины Y = Х 2.
Р е ш е н и е . Пусть G(y) — функция распределения случайной
величины Y. Тогда при у > О
G{y) = P { Y < у} = Р { Х 2 < у } = Р { - ^ у < Х < ^ у } =
= F { j y ) - F i - y /у ) = F i ^ y ) = 1 - е-О'ГУтак что плотность распределения
d
ае~а^У
При у < 0, очевидно, G(y) = 0 и g{y) = 0, ибо случайная величина Y не принимает отрицательных значений.
9. Доказать, что любая функция распределения не может иметь
более чем счетное число точек разрыва.
Р е ш е н и е . В силу монотонности и ограниченности функция
распределения может иметь только разрывы 1-го рода, т. е. скачки
на конечную положительную величину. Все скачки можно перечислить, если перенумеровать их в следующем порядке: сначала
все скачки, большие 1/2 (такой скачок может быть только один,
ибо сумма скачков не может превышать единицу), затем все скачки, большие 1/3 (таких скачков не может быть больше двух),
затем — большие 1/4 (таких скачков — не более трех), и т.д. Таким образом, оказывается возможным установить взаимно однозначное соответствие между множеством скачков и множеством
натуральных чисел, что и доказывает требуемое утверждение.
10.
Функция F(x) называется равномерно непрерывной на
множествеX, если Ve > 0 3 5 > 0, такое, что \F(x\) — F(x 2 )\ < е,
если только \х\ —хг| < 5 и Х\,Х 2 £ X. Пусть F(x) является функцией распределения и пусть она непрерывна в каждой точке. Доказать, что она равномерно непрерывна на всей прямой
—ОО < X < +оо.
Р е ш е н и е . Выберем произвольное е > 0. В силу монотонности функции F(x) и ее свойств lim F(x) = 1, lim F(x) = О
X —+ + Q O
X — ►— OO
можно утверждать, что ЭМ > 0, такое, что колебания функции F(x) в промежутках (—оо, —М] и [М, +оо) не превышают
значения г/2:
Ух', х" £ (—оо, - М ]
Ух',х" £ [М, +оо)
|F{x') - F(x")| < £~,
2
\F(x')- F{x")\ <
(4)
По условию функция F(x) непрерывна на [—М ,М \ . Значит (по
известной теореме Кантора), она равномерно непрерывна на
1
-м ,м у.
38 > 0
Ух', х" G [-A f,М]
|F(x') - F{x")\ < | при |х' - х"\ < 8 .
(5)
Возьмем теперь два любых значения х\ и Х2 из интервала (—оо, +оо).
Покажем, что если \ х \ — хг| < 5, то \F(X\) — F(x 2 )\ < е. Если
Х\,Х 2 € (—оо, —М] или Х\,Х 2 £ [—М,М] или Х\,Х 2 £ [М, +оо), то
требуемое установлено выше. Осталось рассмотреть две ситуации:
1) х\ £ (—оо, - М \ ,
2) Х\ £ (—М,М),
х 2 £ (- М , М );
Х2 G [Л1,+оо).
В ситуации 1) имеем
|F(Xl) - F( x 2)I = |F( x 2) - F(—M) + F ( - M ) - F(xy)| =
= № 2) - F ( - M ) ) + ( F( -M ) - F(Xl)).
Поскольку —М €
( X l , X 2 ) , ТО \Х 2
— (—М)\ < S и в силу (5)
F ( x 2) - F ( - M ) < -£.
В то же время в силу (4)
F ( - M ) - F ( Xl) < e-.
Значит,
\F{ x x ) - F { x 2) \ < £- + £- = 8 .
Аналогичными рассуждениями этот результат устанавливается
и для ситуации 2). Утверждение доказано.
§ 6. Числовые характеристики
случайной величины
1.
Математическое ожидание. Рассмотрим дискретную слу-
чайную величину X с конечным спектром, закон распределения
которой задан таблицей
XI
*2
xk
Р\
Р2
Pk
Пусть проведены л экспериментов, в результате которых п\ раз
реализовалось значение х\, щ раз — значение х 2, . . . , л* раз —
значение х&, так что п\ + Л2 + . . . + пк = л. Среднее значение случайной величины X в данной серии из л экспериментов естественно определить как среднее арифметическое
(1)
Будем теперь безгранично удлинять серии экспериментов, что
формально соответствует условию п —> оо. Тогда в соответствии
с классическим определением вероятности
п
г, П2
Ри ^
Р2 ,
Пк
п
Pk,
а выражение (1) стремится к сумме
х\Р\ + х 2р 2 + . . . x kpk.
(2)
Сумма (2) называется математическим ожиданием дискретной
случайной величины X и обозначается M X или М{Х}. Если X
дискретная случайная величина с бесконечным спектром, то ее
математическим ожиданием называется сумма ряда
J 2 XiPi’
i= 1
если этот ряд сходится абсолютно. В противном случае говорят,
что случайная величина X не имеет математического ожидания.
Пусть теперь X — непрерывная случайная величина с плотностью распределения f{x). Будем пока для определенности считать, что множество возможных значений X принадлежит отрезку [а, Ь\. Разобьем отрезок [а, Ь] на более мелкие промежутки
точками Х\,Х 2 , . .. , х п-\:
а = xq < х\ < Х2 < . .. < х п- \ < х п = Ь.
*k
Пусть pk = P{xk-1 < X < Xk} = [ f(x) dx, k = 1,2, . . . , п. По тео~
„
реме о среднем 3xk G {xk_\,Xk), такая, что что pk =/(х&)Дх&,
где A x k = X k ~ X k - \ . Рассмотрим вспомогательную дискретную
случайную величину X , определяемую законом распределения
X k ~ x
XI
р
*2
Хп
1 Р2
Рп
Случайную величину X можно рассматривать как некоторую
дискретную аппроксимацию непрерывной случайной величины X ,
причем эта аппроксимация тем точнее и полнее, чем больше п.
Математическое ожидание случайной величины X равно
MX = f^Xif(xi)Axi.
i= i
При п —>ос сумма справа стремится к интегралу
ь
| xf{x) d x ,
а
который естественно принять за определение математического
ожидания случайной величины X.
Итак, для непрерывной случайной величины X по определению
MX =
J xf{x) dx,
где интеграл берется по всей области возможных значений случайной величины X. Если эта область неограничена, то интеграл
понимается в несобственном смысле, причем предполагается, что
интеграл сходится абсолютно. В противном случае говорят, что
математическое ожидание не существует.
Можно показать, что математическое ожидание обладает следующими свойствами.
1) Математическое ожидание константы равно этой константе:
М{С} = С.
2) Постоянный множитель можно выносить за знак математического ожидания:
М {С -Х } = С-М{Х}.
3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
М { Х { + Х 2 + .. . + Х п} = М { Х i} + М { Х 2} + . .. + М { Х п}.
4) Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий
сомножителей:
М { Х хХ 2 . . . Х п} = М { Х х} М { Х 2} . . . М { Х п}.
По определению, случайные величины Х \ , Х 2, . .. , Х п называются
независимыми, если для любой группы Xil 9Xi2, - . - , X ik этих величин независимы всякие k событий вида {Х^ Е #i}, {Xi 2 е В 2} , . ..
. . . , {Xik g Bk}, где B \ 9В 2, . . . , Bk — подмножества действительной оси.
5) Пусть X — дискретная случайная величина с законом распределения
Xi
Х2
pi
Р2
Пусть ф(х) — некоторая функция, причем все возможные значения случайной величины X входят в область определения функции ф(х). Тогда для случайной величины Y = ф(Х) математическое ожидание
M Y = ' £ p i (Kxi).
i
6) Если X — непрерывная случайная величина с плотностью
распределения /(х), то для случайной величины Y = ф(Х) математическое ожидание
Рассмотрим ряд примеров на нахождение математического
ожидания.
Пусть X — случайная величина, распределенная по биномиальному закону с параметрами п и р . Найдем MX. Для этого рассмотрим п вспомогательных случайных величин Х \ , Х 2 , . . . , Х п,
которые определим следующим образом. Случайная величина Xi,
i=
может принимать только два значения 0 и 1,
а именно:
J О,
г = III,1
если в г-м эксперименте произошла неудача;
если в г-м эксперименте имел место успех.
Тогда все Xi, i = 1,2, . . . ,п, имеют один и тот же закон распределения:
0
1
1- р
р
Значит, для любого i — 1,2, . . . , п имеем M X —0- (1 —р) + 1-р = р.
Кроме того, очевидно,
X = Х\ + Х 2 + . .. + Х п.
Следовательно,
M X = MXi + М Х 2 + .. . + М Х п = пр.
Пусть теперь X — случайная величина, распределенная по
геометрическому закону с параметром р. Тогда
ОО
ОО
M X = Y 2 kqk- lp = p ^ k q k- 1,
k=\
(3)
k=\
где q = 1 - р. Чтобы найти сумму ряда (3), рассмотрим вспомогательный ряд
оо
Е ?*-
k=l
Последний представляет собой бесконечную геометрическую прогрессию с положительным знаменателем q < 1 и первым членом
b\ = q. Значит,
00
Дифференцируя обе части этого равенства по q, получим
В выражении слева можно поменять местами порядок суммирования и дифференцирования:
ОО
ОО
k= \
ОО
k= l
k= \
так что с учетом (4)
1
Е ^ -1
k=\
В результате из (3) найдем
MX
1
1
1
р2
Р
= Р • ----------5- = Р • - S = - .
(1 ~ q f
И
И
Найдем теперь математическое ожидание случайной величины X, распределенной по закону Пуассона с параметром А. Имеем:
00
\k
\k
M X = ^ 2 k J \ e A= Y
k= 0
“
( k - l ) \ e X = Xe
1
k= l
E
\k -i
(k - 1)!'
k= \
Как известно,
x
x}
x^
ex = \ + - + — + — +
1!
2! 3!
при любом x (разложение экспоненты в ряд Маклорена). Поэтому
°° \*-1
\
\ 2 лЗ
V — ___ = 1 + - + — + — +
2 L f (k
( k -- 1)!
П!
1! 1! 2!2! ^ 3!3! ^
А *
1 ......=
{ +
-
+
—
+
—
‘••
=вА
k-
оо
MX = \е~х V
^
k= \
\к-\
- ■■
— = \ е ~ х • еА = А.
(k - 1)!
Перейдем к вычислению математических ожиданий непрерывных распределений, введенных в § 5. Если X распределена равномерно на отрезке \а,Ь], то
h
ь
х
#
а+ b
ах = — .
Если X имеет показательное распределение с параметром Л, то
Н-оо
+оо
xf(x) dx =
м х =
о
х • Хе Xxdx =
о
л
Наконец, если X имеет нормальное распределение с параметрами а и а, то
+00
f xf(x) dx = [ x _ ^ e-(x-a) 2/V°2) d x .
J
J y fb ta
+00
МХ=
Сделав в последнем интеграле замену х — a — t, получим
+оо
м х =
l ± J L-еe- t2/ {2°2)dt =
v 2 i г аг
+оо
+оо
_ L ^ e-t>/№) dt + a
_ Д _ е-^/(2<т2) dt.
V2тгст
„ л/2тга
(5)
Интеграл
+оо
t2H2o*)dt
V 2
tto
равен нулю как интеграл от нечетной функции по симметричному
промежутку. Интеграл
+оо
f - J ^ e - t2/ ^ 2U t = \ ,
J
у
27ГСГ
поскольку последнее равенство выражает условие нормировки
для нормальной плотности распределения с нулевым значением
параметра а. С учетом этих обстоятельств из (5) получаем
M X = а.
2.
Д исперсия. Дисперсией произвольной случайной величины X называется число
т. е. математическое ожидание квадрата отклонения случайной
величины X от ее математического ожидания MX. Если X —
дискретная случайная величина с законом распределения
х\
*2
Р\
Р2
то по свойству 5) математического ожидания
DX =
- M X f Pl.
i
Если же X — непрерывная случайная величина с плотностью
распределения f(x), то по свойству 6) математического ожидания
DX = (х - MX) f(x) dx,
где интеграл берется по всей области возможных значений случайной величины X.
Преобразуем правую часть равенства (6):
М { ( Х —M X ) 2} = М { Х 2 —2Х ■M X + {MX)2} =
= М { Х 2} - 2M X ■M X + (MX ) 2 = М { Х 2} - (MX)2.
Таким образом, для любой случайной величины X
DX = М { Х 2} - (MX ) 2
(7)
— дисперсия случайной величины равна математическому ожиданию ее квадрата минус квадрат ее математического ожидания.
Заметим, что в силу определения (6) DX > 0, так что из (7)
получаем
М { Х 2} > (ТИХ)2,
т. е. для любой случайной величины математическое ожидание
квадрата не меньше квадрата математического ожидания.
Нетрудно установить следующие свойства дисперсии.
1) Прибавление константы к случайной величине не меняет ее
дисперсии:
D { Y + С} — DY.
2) Постоянный множитель выносится из-под знака дисперсии
в квадрате:
3)
Дисперсия суммы независимых случайных величин равна
сумме дисперсий слагаемых:
D {X j + Х 2 + . . . + Х п} = DX 1 + DX2 + . .. + DXr(.
Докажем, например, свойство 3). Достаточно ограничиться
случаем двух слагаемых. Имеем:
D{X 1 + Х 2} = М{ {Х х + Х 2) - М(Х 1 + Х 2) } 2 =
= М {{Х х - М Х х) + (Х 2 - М Х 2) } 2 =
=
М { { Х х - М Х х) 2 + ( Х 2 - М Х 2) 2 + 2 ( Х х - M X i ) ( * 2 - M X i ) } =
= M { ( X x - M X x ) 2 } + М { ( Х 2 - М Х 2) 2 } +
+ 2М{{Хх - М Х х){Х2 - М Х 2)} =
= DXx + DX2 + 2М{(Хх - M X i)(X 2 - М Х 2)}.
В силу независимости случайных величин Х\ и Х 2
М { ( Х 1 - М Х 1){Х2 - М Х 2)} =
= М { Х хХ 2 - Х хМ Х 2 - Х 2М Х х + М Х хМ Х 2} =
= М Х хМ Х 2 - М Х хМ Х 2 - М Х 2М Х х + М Х хМ Х 2 = о,
так что D{X 1 + ^ 2} = D Xx 4- DX2, ч. т. д.
Найдем дисперсии распределений, введенных в § 5. Пусть X —
случайная величина, распределенная по биномиальному закону
с параметрами п и р . Используем представление (см. выше)
Х = Х х + Х 2 + . . . + Х п,
где Х х, Х 2, .. . , Х п — независимые дискретные случайные величины, каждая из которых может принимать только два значения: О
с вероятностью 1 —р и 1 с вероятностью р. По свойству 3) имеем
DX = DX x + D X 2 + . . . + DXn.
Поскольку
DX x = D X 2 = . . . ^ DXn = (0 - р ) 2 • (1 - р ) + (1 - р ) 2 -р = р( 1 - р ) ,
то получаем
D = tipq,
где q = 1 —р.
Пусть теперь X — случайная величина, распределенная по
геометрическому закону с параметром р. Для нахождения DX
воспользуемся тождеством (7). Ранее установлено, что M X = 1/р.
Далее,
ОО
ОО
M X 2 = £ k 2 qk~lp = р<Г k 2 qk~K
k= \
k= l
Как и при вычислении математического ожидания геометрического распределения, рассмотрим ряд
оо
гЛ
k=\
дифференцируем обе части по q и меняем порядок суммирования
и дифференцирования слева:
ОО
1
J k y k q k~l = ------- , ,
h
а - -?)2
1
1
умножаем обе части на q:
ОО
снова дифференцируем обе части по q и меняем порядок суммирования и дифференцирования слева:
У k 2 qk~x = (
q
^ -
1+
q
Следовательно,
MX2 = Р у
к= \
k 2 qk~l =
Р
Р
Пусть X — случайная величина, распределенная по закону
Пуассона с параметром А. Вычислим ее дисперсию, воспользовавшись тождеством (7). Для этого найдем
°° > a V a
_ , ^ k 2Xk
*“ 2 = Е ‘ 2 ± ^
= * - АЕ ^ '
k= 0
k= 0
(в)
Рассмотрим вспомогательный ряд
А'
Е k\
А
;
k=0
дифференцируем обе части по Л и меняем порядок дифференцирования и суммирования слева:
E
k=0
kX\ k - \
k\
\
умножаем обе части на Л:
k=0
дифференцируем обе части по Л и меняем порядок дифференцирования и суммирования слева:
Е
k=0
k X
k\
Ае + е ,
откуда, умножая обе части на А, имеем
00 ь2\*
S T ~ = \ e x + X2 e \
k\
k=0
так что, учитывая (8), получаем
М Х 2 = е_Л(АеЛ + А2ел) = А + А2
И
DX = М Х 2 - {МХ ) 2 = А + А2 - А2 = А.
Заметим, что для распределения Пуассона DX = МХ.
Обратимся теперь к непрерывным распределениям, рассмотренным в §5. Если X — случайная величина, равномерно распределенная на отрезке [а, Ь\, то по определению
(
a + b\ 2 1 ,
i b - a )2
x — —
dx =
12
V
2 ) b-a
Для случайной величины X, распределенной по показательному закону с параметром Л,
+00
DX
= J(jc — M X ) 2f{x) d x =
( * _ I ) A e~Xxdx = ^ .
0
Наконец, для случайной величины X , имеющей нормальное
распределение с параметрами а и сг,
+оо
DX =
J( x
- M X ) 2f{x) dx —
i x - a ) 2 ^ =_ e-(^-a)2/(2<T2) d x .
сделаем замену переменной интегрирования:
х —а
а
— t,
х = at + a,
dx — cr dt\
тогда
+оо
+оо
№
DX =
у 2ж
-* 2/ 2 d t = ^ =
V27T
— ОО
сг2
V 2 tt
+
+о
оо
о
i - t e - * ! 2)
2
+оо
Н-оо
^ е t2l 2 dt.
+ *
\[Ък .
Поскольку
4-оо
1
-/2
e~^dt=l
— условие нормировки для плотности нормального распределения
с параметрами а = 0 и а = 1, то получаем
DX = a 2.
Таким образом, параметры а и а в выражении для плотности
нормального распределения
fix) =
1
-(х—а)2/(2сг2)
(9)
жег
у/Ъ*
имеют следующий смысл: параметр а есть математическое ожидание, а а 2 есть дисперсия соответствующей случайной величины X.
Наряду с дисперсией используется также понятие среднеквадратичного отклонения случайной величины, которое определяется как \ [ Ш — корень из дисперсии. Следовательно, а
в выражении (9) имеет смысл среднеквадратичного отклонения
случайной величины X.
В заключение сведем в единую таблицу числовые характеристики изученных распределений (табл. 2).
Таблица 2
Распределение случайной величины
X
MX
DX
пр
npq
1
Р
Я
р2
Л
Л
а+Ь
СЬ - а )2
12
Биномиальное:
Р{х = т} = Cknpmqn~m,
т = 0,1,2, . . . , п\ q = 1 — р\ п,р — параметры:
п е N, р е [0, 1]
Геометрическое:
Р{Х = т} = qm~lp,
т = 1,2, . . . , п; q = 1 —р\ р — параметр, р е (0,1]
Пуассона:
Хте~х
=
/л! '
т — 0,1,2, ...; Л > 0 — параметр
Равномерное на отрезке:
[
/(*) = { ь ~ а
[ 0,
х С [а , 6],
хф [а ,Ь ].
2
а,Ь — параметры: b > а
Показательное:
0,
х < 0,
/(*) = {
\ е ~ Хх, х > 0;
1
1
А
3?
а
а1
Л > 0 — параметр
Нормальное:
/(* )=
J_
л/27ГСГ
а, сг > 0 — параметры
Задачи
1.
Правильный шестигранный кубик из однородного материала с пронумерованными гранями бросают до тех пор, пока не
выпадут все грани. Найти математическое ожидание и дисперсию
числа бросаний.
Р е ш е н и е . Пусть X — случайная величина — число бросаний
к моменту выпадения всех граней. Заметим, что X можно представить в виде суммы:
* = * 1 + * 2 + Х3 + * 4 + Х 5 + * 6 ,
где:
,
Х\ = 1 — неслучайная величина; r
<!ГГ , д . ,
Х 2 — случайная величина — число бросаний, отсчитываемое от второго бросания до момента t% (включительно) выпадения какой-либо грани, отличной от той, что выпала при первом
бросании;
Хз — случайная величина — число бросаний, отсчитываемое
после момента ^ ДО момента to, (включительно) выпадения какойлибо из 4 оставшихся граней, ни разу не выпадавших с начала
эксперимента;
Х§ — случайная величина — число бросков, отсчитываемое
после момента t$ до момента ^ (включительно) выпадения последней из 6 граней, ни разу не выпадавшей с начала эксперимента.
Ясно, что Х 2 , Х з , Х 4 , Xs,Xq — независимые случайные величины, распределенные по геометрическому закону, но с различными
значениями параметра р: Х 2 — со значением р = 5/6, Х^ — со значением р = 4/6 , Х 4 — со значением р = 3/6, Х$ — со значением
р = 2/6, Xq — со значением р = 1/6. Поэтому
M X = МХ\ + M X 2 + M X 3 + M X 4 + М Х 5 + М Х 6 =
-
—
—
— —
1 _
+ 5/6 + 476 + 3/6 + 2/6 + 1/6 ~
Для дисперсии получаем
DX = DX\ + DX 2 + DX 3 + DX 4 + DX5 + DX 6 =
= 0 4- _ J /6_ + J / ! . + J Z L 4 J Z L 4 J / 6_ = ад ад
(5/6)2 (4/6)2 (3/6)2 (2/6)2 (1/6)2
2.
Человек, имеющий п ключей, хочет отпереть свою дверь,
испытывая ключи независимо один от другого и в случайном порядке, причем неподошедшие ключи не исключаются из дальнейших испытаний. Известно, что только один из имеющихся ключей
подходит к замку. Найти математическое ожидание и дисперсию
числа испытаний.
Р е ш е н и е . Пусть X — число выполненных попыток до момента открывания двери включительно. Тогда, очевидно, случайная величина X распределена по геометрическому закону с параметром р — \ j п. Следовательно,
М Х = - = п,
р
DX = “—2~ = п(п - 1).
р
3.
Решить задачу 2 при условии, что неподошедшие ключи
исключаются из дальнейших испытаний.
Р е ш е н и е . Пусть по-прежнему X — случайная величина —
число выполненных попыток до момента открывания двери включительно. Тогда возможные значения X есть 1,2, . . . , я . Найдем
соответствующие вероятности. Ясно, что
Р {Х = 1} = - .
п
Далее, пусть событие Л/, / — 1,2, . . . , п, означает, что i-я попытка
оказалась удачной, так что событие
означает, что i-я попытка
оказалась неудачной. Тогда
Р{ Х = 2} = />{Л,Л2} = Р{А 2 И ,} Р { Л ,} = - J - j . 4-1 =
1,
Р{ Х = 3} = Р {А {А 2 А 3} = Р { А 3 1Л 2Л ,}Р {Д 2 1Л,}/>{Л,} =
1
п —2 п —1
1
п —2 п — 1
п
п
Аналогично рассуждая, получим
Р {Х = А} = Р { Х = Ь} = . .. = Р{ Х = п } = Х
-.
Следовательно,
Поскольку
•
^
и2 _
п(п +
1 )(2 п
5
+
1)
— известная числовая сумма, то получаем:
p iy
(az +
~
1)(2az +
1)
(п -f-1 )2
6~
4
л? — I
~
12~*
4.
Брошены две игральные кости. Найти математическое
ожидание суммы выпавших очков, если известно, что выпали
разные грани.
Р е ш е н и е . В этой задаче речь идет о вычислении условного
математического ожидания дискретной случайной величины. Это
понятие вводится следующим естественным образом. Если дискретная случайная величина X принимает значения
то
условным математическим ожиданием случайной величины X
при условии, что произошло событие Л, называется число
M { X \ A } = Y t x iP{ X = x i \A},
i
если ряд справа сходится абсолютно (в случае случайной величины с конечным спектром вместо ряда будет конечная сумма
и вопрос о сходимости отпадает).
Пусть # ь # 2 , - - ч Н п — полная группа событий. Тогда по формуле полной вероятности
Р {Х = Xi} = £ / > { * = Xi | Hj} P{Hj).
м
Рассмотрим
M X = ' £ x i P { X = xi}.
i
Подставив вместо вероятности Р{ Х = xf} ее разложение по формуле полной вероятности, найдем
M X = Х > £ Р { * = Xi I Hj}P{Hj} =
i
j=1
=
= * IЩ Р Щ } = £ I > m
/=i ;
i /=i
=
Ёp № E * p{x
=
I
=
= *i\Hj ) = Y / M { x \ H l } p(Hj}.
Таким образом, для любой полной группы событий Н\,Н2, ... ,Н п
МХ = ^ М { Х Щ } Р Щ }
/=1
— получили аналог формулы полной вероятности для математических ожиданий.
Вернемся к решению задачи 4. Пусть Х\ — число очков, выпавшее на одной кости, X 2 — на другой. Пусть событие А означает, что выпали разные грани. Тогда
М { Х х + Х 2} = M { X i + Х 2 \ А } Р { А } + М { Х х + Х2 | А} Р { А} .
Искомое математическое ожидание есть М{Х\ + Х 2 \ А}. Очевидно,
М Х х = (1 + 2 + 3 + 4 + 5 + 6) • i = 7~,
M X 2 - MXi = 7~,
M{Xi + X 2} = 7.
Далее,
M{Xi + X 2 | A} = 2 • i + 4 • i + 6 • i + 8 • i + 10 • i + 12 • i = 7.
Следовательно,
7 = M { X x + X 2 \ A } - ^ + 7 - -1,
откуда
M { X x + X 2 \A } = 7.
5.
Пусть X — случайная величина, такая, что Р {0 < X < 1} = 1.
Доказать справедливость неравенства DX < MX.
Р е ш е н и е . Поскольку DX = M X 2 — (MX)2, то неравенство
DX < M X эквивалентно неравенству
M X 2 - (MX ) 2 < M X
ИЛИ
M X 2 < M X + (MX)2.
Если X — дискретная случайная величина, то
M X 2 = J 2 X1Н х = X i } < J 2 x i Р{х = x i } = MX,
i
i
ибо 0 < Xi < 1. Если X — непрерывная случайная величина с плотностью распределения /( х), то в силу условия Р {0 < X < 1} = 1
плотность f(x) равна нулю вне промежутка (0,1), так что интегралы при вычислении математических ожиданий берутся по
промежутку от 0 до 1:
MX2
х 2f(x) dx < | xf{x) dx = MX.
Итак, доказано неравенство M X 2 < MX, а значит, и M X 2 < M X +
+ (MX)2.
6.
Пусть X \ , X 2 , .. . — последовательность независимых одинаково распределенных случайных величин с математическим
ожиданием т и дисперсией а 2. Случайная величина Y не зависит
от случайных величин Х \ , Х 2 , . . . и принимает натуральные значения, причем M Y = b, DY = d. Пусть
z -'tx i.
i— 1
Найти M Z и DZ.
Р е ш е н и е . Для решения этой задачи введем понятие характеристической функции. Характеристической функцией произвольной случайной величины W называется функция действительного переменного
f w ( t ) = M { e itw},
(10)
где i — мнимая единица: i2 = —1. Известно, что еслиM { \W \k} < оо
для некоторого натурального k, то
Этот результат получается непосредственно из (10) последовательным дифференцированием обеих частей равенства и использованием свойства перестановочности операций взятия математического ожидания и дифференцирования.
Вернемся к решению задачи. Найдем условную характеристическую функцию fz(t | k) случайной величины Z при условии Y = k:
fz(t | k) = M { e itz | Y = k } = M { e it(x‘+x*+•■•+**)} =
= M { e itx' } M { e itXi) .. . M { e itXk} = (fx (t))k,
где fx(t) — характеристическая функция случайной величины Xj
для любого / = 1 , 2 , __ Для безусловной характеристической
функции fz(t) имеем
оо
оо
Ш ) = £ / z ( * | k ) P { Y = k} = J2(fx(t))kPk,
k=\
k=\
где pk = P { Y = k}.
Найдем математическое ожидание. Имеем
iMZ =
dfz(t)
dt
t= 0
=Ё
t= 0
k= \
= J 2 kpk dfxit)
dt t=о
k= \
dfxit)
dt
■J 2 kPk = iMX ■M Y >
*=° k=\
откуда
J
M Z = M X ■M Y = mb.
Для нахождения дисперсии воспользуемся тождеством DZ
= M Z 2 - {MZ)2. с этой целью найдем 7WZ2:
? т
2
=
dt 2
t=о
=
= f ; kPh [(л - \)ifxit ) ) k - 2 ( ^
k=\
) 2 + ifxit))k- 1^ ^ t= 0
2
k= \
d 2fx it)
dt
/=oJ
= Y , kPb((k - 1W M X ) 2 + i2M X 2) =
k=\
= i2M x 2 ^ 2 k p k + iiMX)2 ^ 2 i k - i ) k p k.
k=i
k=i
Поскольку M X = m, M X 2 = DX 4- iMX ) 2 = a 2 + m2, то получаем
OO
M Z 2 - (a 2 + m2)
OO
kpk + m2 ]T (£ ~ V kPk-
k=\
Далее,
OO
k=\
kpk = M Y = 6. Осталось найти сумму ^ { k — 1)kpk'ь=1
k=\
OO
OO
J2ik~ l)kpk = 52k2pk-J2kpk=
6=1
6=1
k=\
= M Y 2 - M Y ■.= DY + i M Y ) 2 - M Y = d + b2 - b.
Таким образом,
M Z 2 = (а 2 + m2)b + m2{d + Ь2 - b) = a 2b + m2d + т 2 Ь2,
так что
DZ = M Z 2 - СMZ)2 == a 2b + m 2 d.
7. Пусть число N падающих на единицу поверхности тела за
время т, имеет распределение Пуассона с параметром Ат, где А —
постоянная, называемая интенсивностью потока частиц. Каждая частица независимо от других сообщает телу энергию е, равномерно распределенную на отрезке [0, с]. Найти математическое
ожидание и дисперсию энергии, получаемой единицей поверхности тела за время т.
Р е ш е н и е . Энергию, получаемую единицей поверхности тела
за время т, можно представить случайной величиной
Z = £\ +
£2
+ • • . + £/V>
где случайная величина N — число частиц, упавших на единицу
поверхности за время т, е-ь — случайная величина — энергия,
переданная /-й упавшей частицей, / = 1,2, ...,ЛЛ Поскольку
равномерно распределена на [0, с], то
Af* = £,
Det = f 2 .
Поскольку случайная величина N распределена по закону Пуассона с параметром Лт, то
M N = D N = Ат.
Наконец, в силу того, что случайные величины N , e \ , £ 2 , . .. независимы, можно воспользоваться результатом решения задачи 6
и написать:
M Z = М£{ ■M N = С
- \ т,
DZ = Dst ■M N + (Me*)2 • DN = ^ А т + ^ А т =
8 . Рассмотрим испытания Бернулли с переменной вероятностью успеха. Пусть Х \ , Х 2 , . ■■, Х п — независимые случайные величины, такие, что X * принимает значения 1 или 0 с вероятности-
ми соответственно pk и
DXk — QkPk- Положим
= 1- р
Тогда, очевидно, MXk = pk,
S n = Xi + X 2 + . .. + X n.
Случайную величину S n можно рассматривать как число успехов
в серии испытаний Бернулли с вероятностью успеха pk в k -м
испытании, k = 1,2, . . . , п. Имеем
MSn =
pk,
k=\
DSn = Y QkPkk=\
Величину p = (pi + p 2 + .. . + pn)/n естественно назвать средней
вероятностью успеха. Как изменится дисперсия DSn при переходе к обычной схеме Бернулли, когда р — вероятность успеха в
каждом испытании — постоянная величина?
Р е ш е н и е . Перепишем результат для DSn в виде
DSn = Y ( l ~Pk)pk = Y p k - Y , p I = пр - Л р 1 k=\
k=l
k=l
k=\
О 1)
n
Из всех комбинаций pk, k = 1,2, . . . , n, таких, что Y P k = np.
П
k=l
сумма
имеет наименьшее значение, когда все pk равны.
k=i
Действительно, рассмотрим задачу на условный экстремум:
п
п
Y p I -*• т *п
k=\
ПРИ условии
Y P k = пРk=\
Вводя функцию Лагранжа
1
= Х > 1 + А(Х > * ~ пР)
ы\
k=\
и записав необходимое условие условного экстремума
найдем
2р\ + Л — О,
2Pk + А = О,
п
Y , p k - n p = o,
k=\
откуда
Р\ + Р2 + • • • + Рп
Р\ = Р2 = • • • = Pk = —
П
То, что это точка минимума, следует теперь из условия (обозначим A p k = p k - p )
+ Др*)2 - f > 2 > О,
k=\
k=\
ибо левая часть неравенства преобразуется к виду
£ 2p A p k + Y , ( A Pk) 2 = 2p J 2 A Pk + 1 2(A P k f = 52 ( A Pk)2k=l
k=l
k=\
k=l
k=\
n
n
Здесь учтено, что
Apk = 0, поскольку Y^Pk = const.
k=\
k=\
Вернемся к равенству (11). Получается, что если средняя вероятность успеха р остается постоянной, то дисперсия случайной
величины S n достигает максимума при Р\ = р 2 = ■■■= рп — Р- Таким образом, получен неожиданный результат: изменение значений pk, или их неодинаковость, уменьшает величину случайных
флуктуаций, которая характеризуется дисперсией. Например, число пожаров в городе за год можно рассматривать как случайную величину; при фиксированном среднем значении вероятности
пожара строений дисперсия числа пожаров максимальна, если
вероятности пожара для всех строений одинаковы.
9.
Деревья в лесу растут в случайных точках, которые образуют пуассоновское поле с плотностью А (среднее число деревьев
на единицу площади), так что вероятность того, что участок леса
площадью S содержит ровно т деревьев, равна ( \ S ) me~xs/ т\,
т = 1 , 2 , . . . . Выберем произвольную точку О в этом лесу. Пусть
случайная величина R — расстояние между точкой О и ближайшим к нему деревом. Найти математическое ожидание MR и дисперсию DR.
Р е ш е н и е . Найдем функцию распределения F(r) случайной
величины R. Для этого проведем вокруг точки О окружность
радиуса г. Для того чтобы расстояние R от этой точки до ближайшего к ней дерева было меньше г, надо, чтобы в круг попало хотя
бы одно дерево. Пусть событие А означает, что в круг радиуса г
с центром в т. О попало хотя бы одно дерево. Тогда
F(r) = P{R < r } = Р{А} = 1 - Р{А} = 1 - е - жг2х.
Следовательно, плотность распределения /(г) случайной величины R
.
dF(r)
Г2тгАге~жХг\
г > 0;
= ~ d T = | 0,
г<0.
Поэтому математическое ожидание
Н-оо
MR =
Н-оо
г /(г) dr = | 2-7rAr2e 7гАг2dr ■
о
о
+00
Н-ОО
Н-ОО
rdfe-***) = (-re -"* * ) | о ° ° + j e~*Xr2 d r = | e~r>j3 dr.
о
о
о
Для вычисления последнего интеграла введем новую переменную
интегрирования t = Ы2пХ. Тогда
Н-ОО
MR =
Н-ОО
1
e ~
t2! 2 d
t
х/2тгЛ
0
Вычислим теперь дисперсию:
=
1
л/Л
.
0
Н-оо
DR = M R 2 - ( M R ) 2 =
Jt 2 f ( r ) d r - \ ^ - \
— e~t2/ 2 d t = —
y/bc
2VA'
2
1
+ °°
=
| 2 тг\г3 е ~ * Хг2 d r - - ^ .
о
о
Вводя новую переменную интегрирования и = г2, получим
Н-оо
Н-ОО
DR
^
= J тгАue-* Xad u -
Н-оо
^ = | u d { - e ~ nXu) - -^ =
о
о
Н-оо
= ( - и е ~ ”Хи)
|о°°+ J e~*Xud u - - ^
о
1
7гЛ
-А и | +0° -
1о
-
4А
=
—
7гА
-
-
4А
=
—
47гА
.
10.
Некоторая урна содержит шары с номерами от 1 до N.
Пусть X — наибольший номер, полученный при п извлечениях,
если производится случайный выбор с возвращением. Найти MX.
Р е ш е н и е . Пусть случайная величина Х х — номер вынутого
шара при г-м извлечении, г = 1,2, . . . , п. Тогда
X = т а х { Х ь ^2, • • • ,Хп}По определению
N
M X = Y , k P { X = k}.
k=\
Найдем Р{ Х = k}. Для этого рассмотрим вероятность
Р { Х < k} = Р { т а х { Х и Х 2, . . . , Х п} < k } =
= Р { Х х < k , X 2 < k , . . . , Х п < 6 } (1).
В силу независимости случайных величин Х \ , Х 2, . ■. , Х п последняя вероятность равна произведению
Р { Х х < k } P { X 2 < k } . . . P { X n < k } = ( А ) я,
так что
Аналогично
р {х < k
- 1} = ( * ^ 1 ) " .
Теперь заметим, что поскольку X может принимать только натуральные значения, то
Р{ Х < k } = P { X < k - 1} + Р { Х = k},
откуда
^ Перечислением событий через запятую обозначается их произведение.
Следовательно,
MX = j r k P { x = k} = ' £ k" * ' - * < * - ' r =
k= \
k= \
= ^ ' t { k n + l - ( ( k - l ) + l ) ( k - l ) n) =
k —\
= ^ f : ( k n+i- ( k - i ) n+i- ( k - i r ) =
k=\
= i
( x > “+ ' - <* - 1)“+1) - £ ( * - D”) =
\= l
k= \
При больших N последняя сумма приближенно равна площади
области, лежащей ниже кривой у = х п и ограниченной прямыми
х = 0 и х = N, т. е. величине
N х ПИ
dx = ^
/2+1
о
Поэтому при больших N
М Х ъ ^ - ( V + 1= — N.
N \
/2 + 1/
/2 + 1
Если в городе имеется N — 1000 машин и производится случайная выборка объемом п = 10, то математическое ожидание
максимального наблюденного регистрационного номера приближенно равно 910. В прикладной статистике наблюденный максимум выборки используется для оценки неизвестного истинного
значения N.
11.
Пусть случайная величина Y имеет нормальное распределение с математическим ожиданием M Y = а и дисперсией DY = а2.
Рассмотрим случайную величину X = eY, так что Y = InX. В этом
случае говорят, что случайная величина X имеет логарифмически нормальное (логнормальное) распределение. Требуется найти
функцию распределения, плотность распределения, математическое ожидание и дисперсию случайной величины X.
Р е ш е н и е . По определению, функция распределения F x ( x )
случайной величины X есть
Fx (х) = Р { Х < х } = Р { е у < х}.
При х < 0 эта вероятность равна нулю. Считая далее х > 0, имеем:
In*
P { e Y < x } = P { Y < \п х } =
та
Переходя к новой переменной интегрирования z = (t — а)/а, последний интеграл можно представить в виде
( I n * — а)/<т
1
е z2/ 2dz
л/27Г
( l n x —а)/ст
1 .-*2
е ~ * '2 dz +
V2n
^ d z = ' - + ф ( 1р7 ° ) .
где
Ф(и) =
=e~z2?2 dz
\/ 2 ^
4
— табулированная функция Лапласа. Таким образом,
О,
Fx (x) = < 1 , , / In* - а \
Н + Ф ( — -— J ,
.2
\
х < О,
.
х > 0;
Для плотности распределения fx(x) случайной величины X
получим
f (v\
dFx(x)
Ш
=
О,
х < 0;
<
1 е-(1п*-а)2/(2<т2)) х > 0.
' Vbrax
Найдем теперь математическое ожидание МХ:
Переходя в последнем интеграле к новой переменной интегрирования и = (1пх —а)/а, получим
+00
+оо
МХ =
1 е~и2/ 2 еаи+а du —
_ } _ е - ( и 2-
2 сп1+сг 2) / 2 +<т2/ 2 + а
^
_
Н-оо
= е а 2/ 2 + а
[Г _Л L= е J \/27Г
( ^ )
Аналогичные вычисления для дисперсии
Н-ОО
DX =
(х —MX) fx(x) dx
дают следующий результат:
DX = е 2а+а\ е а - 1).
2П (1и
= е (т2/2+а.
Совокупность п случайных величин ( Х \, Х 2, . . . , Х п), рассматриваемых совместно, называется системой п случайных величин. Функцией распределения F(x\ , х 2, . .. , х п) системы п случайных величин называется вероятность совместного выполнения
системы п неравенств Х\ < х \ , Х 2 < Х2 , . . . , Х п < х п, т. е.
F(x!,Х2, ...,Х„) = Р { Х 1 < Х ! , Х 2 < Х 2, . . . , х „ < Хц}.
Остановимся более подробно на случае п = 2, а систему
( Х \ , Х 2) будем обозначать (X, У). Функция распределения системы (X, Y) есть
F(x, у) = Р { Х < х, Y < у}.
Она обладает следующими свойствами:
1) lim F(x,y) = 0;
х — >— ОО
у-*-оо
кроме того, для любого значения у
lim F(x, у) = 0;
х — >— ОО
для любого значения х
lim F(x, у) = 0;
У у оо
2) если Fx(x) — функция распределения случайной величины X, a Fy(y) — функция распределения случайной величины У,
то
lim F(x,y) = F Y(y),
x —>-(-oo
при
lim F ( x, у) = Fx (x);
y —>+oo
ЭТО М
lim F{x,y) — 1;
X-^+OO
y -^+ o o
3) F(x, у) — неубывающая функция переменных х н у ,
4) для независимых случайных величин X и У
F { x , y ) = F x { x ) - F Y{y).
Если существует функция fix, у), такая, что функция распределения F(x, у) представима в виде
Л
F i x , у)
у
= J J
f{x,у) dudv,
то функция f{x, у) называется плотностью Совместного) распределения системы (X, 7). Она обладает следующими свойствами:
1) fix, у)
>
0;
2) вероятность попадания случайной точки (X, 7) в какуюлибо область G на плоскости равна
Д/о{х, у) dx dy,
G
3) если функция fix, у) непрерывна в точке ix,y), то вероятность попадания случайной точки iX, 7) в прямоугольник
х < х < х + А х,
у < у < у + Ау
с точностью до бесконечно малых высшего порядка равна
fix, у) А х Ау;
4) если fxix) — плотность распределения случайной величины X, a fyiy) — плотность распределения случайной величины 7,
то
+оо
+00
f i x , y ) d y = fxix),
f i x , y ) d x = f Yiy);
J
— ОО
— ОО
5) для независимых случайных величин X, 7
f i x , у) = fxix) -fyiy)',
6) в точках непрерывности функции fix, у)
f(X и) = д 2р (Х’У)
п ,у>
дхду '
Следующим важным понятием, характеризующим свойства
системы случайных величин, является понятие корреляционного
момента, или ковариации двух случайных величин. Корреляционным моментом Кху, или ковариацией cov(2f, 7) двух случайных
величин X и 7 называется число
cov(*, 7) = М Ц Х - M X ) i Y - MY)}.
Правую часть этого равенства можно преобразовать к виду
M { X Y } — M { X } M { Y } . Случайные величины, удовлетворяющие
условию
cov(Z, У) = 0,
называются некоррелированными. Этому условию, в частности,
удовлетворяют независимые случайные величины. Отметим, что
обратное неверно: из некоррелированности случайных величин,
вообще говоря, не следует их независимость.
Нетрудно показать, что
D { X ± Y } = DX + D Y ± 2 c o v ( X , Y ) .
(1)
В частности, для независимых случайных величин D{X ± У} =
= D X + DY.
Обобщением результата (1) является следующий. Если Х\,
Х 2 , ■■■, Х п — произвольная система случайных величин, каждая
из которых имеет конечную дисперсию, то
D { X x + * 2 + . .. + Х п} = £ DXi + 2 £ соv(Xi, Yj).
i<j
i= l
В частности, если все дисперсии DX и ковариации cov{Xi, Yj)
одинаковы: DXi = d для любого i = 1,2, . . . , п; соv(Xi,Xj) = К для
любых i ф /, то
D { X i + X 2 + . . . + X n} = nd + n ( n - \ ) K .
(2)
Наряду с понятием ковариации используется понятие коэффициента корреляции. Коэффициентом корреляции гху случайных
величин X и Y называется безразмерная величина
„
_ соv(X,Y)
' XU —
(Ух(Уу
>
где ох = VDX, о у = \f~DY. Для любых двух случайных величин
V x y \ < 1- Если случайные величины X, Y связаны линейной зависимостью вида Y = а Х + [3, где а ^ О , (3 — фиксированные постоянные, то их коэффициент корреляции равен 1 при а > 0 и —1 при
а < 0. Для независимых случайных величин X, Y выполняется
?ху — 0Отметим также полезные свойства ковариации, непосредственно следующие из ее определения:
1) cov(aX, У) = cov(X, a Y ) = acov(X, Y), где a = const;
2) cov(X + Y , Z ) = соv(X, Z) + cov(7,Z);
3) cov(Z, Y + Z) = cov{X, У) + cov(X,Z).
Приведем теперь примеры двумерных распределений.
Пример 1. Двумерная случайная величина (X , У) называется
равномерно распределенной в области G, если ее плотность распределения имеет вид:
fix, у)
О,
если (х , у) £ G;
I/Sq ,
если
(x,y)eG .
Здесь S q — площадь области G.
Пример 2. Двумерная случайная величина (X , Y) имеет невырожденное нормальное распределение, если ее плотность распределения представима в виде:
fix, у) =
1
2 жахау\/[
х ехр
X
- г2
(х - а)2
{
2г
2(1 - г2)2 (
(х - а) (у
ахсг.
хи у
b) + (jr Ь)
СГ„
где а, Ь, ох, ау, г — параметры, причем ах > 0, ау > 0, |r| < 1. При
этом параметры а,Ь,ах ,о у,г имеют следующий вероятностный
смысл: а, Ь — математические ожидания случайных величин X, Y :
о = MX, b = MY; <тх,о у — среднеквадратичные отклонения случайных величин X, Y: ах = VDX, ау = VDY; г — коэффициент
корреляции случайных величин X н Y: г = cov(X, Y)/(ax cry).
Задачи
1.
В группе из 15 человек 5 имеют доход 1, другие 5 имеют
доход 2, а оставшиеся 5 человек имеют доход 3. Из данной группы
случайно отбирают двух человек. Найти ковариацию их доходов.
Р е ш е н и е . Пусть случайная величина Х\ — доход первого
выбранного человека, а случайная величина Хч — доход второго
выбранного человека. Тогда искомая ковариация есть
cov{Xx, X 2) = М { Х хХ 2} - М { Х х} М { Х 2}.
Найдем законы распределения случайных величин Х \ , Х 2 и Y —X \ X 2.
Закон распределения случайной величины Х[ очевиден:
Xi
р
1
2
3
1/3
1/3
1/3
Найдем закон распределения для Х 2 . Возможные значения
для Х 2 — это по-прежнему числа 1,2,3. Соответствующие вероятности найдем по формуле полной вероятности:
Р { Х 2 = 1} = Р {Х 2
= 1 1* i =
1} Р { Х х = 1} +
+ Р {Х 2 = l \ X x= 2 } P { X l = 2 } + Р {Х 2 = l \ X x = 3}P {*i = 3} =
- А А А А+ А А - А
~ 14 ’ 3 + 14 ‘ 3
14 ' 3 ~ 3 ’
где в качестве полной группы событий выступают события А/ = 1,
Х\ = 2, Х х = 3. Аналогично устанавливается, что
Р{Х 2 = 2} = А,
р № = 3} = А
т. е. закон распределения случайной величины Х 2 совпадает с законом распределения случайной величины Х\:
Х2
р
1
2
3
1/3
1/3
1/3
Этот результат можно объяснить так. Для наблюдателя, не знающего, какой человек был выбран первым, а какой — вторым,
оба выбранных человека и соответствующие им случайные величины Ai и Х 2 равноценны и, следовательно, последние должны
иметь одинаковые распределения.
Найдем теперь закон распределения случайной величины
Y = X 1X 2 . Ее возможные значения: 1, 2, 3, 4, 6, 9. Найдем соответствующие вероятности. Имеем:
P { Y = l } = P { X l = l,X2 = i} =
= Р{ Х 2 = 1 |Jf, = 1}Р{Х, = 1} = 1 . 1 = 1 .
Аналогично,
^0' = 4 } = | .
P{Y = 9} = А.
Далее,
P { Y = 2} = Р { Х 1 = 1, Х 2 = 2} + Р{Х\ = 2, Х 2 = 1} =
= Р{Х 2 = 2 \ X i = l}P{Ai = 1} + Р{ Х 2 = 1 1*1 = 2 } Р { Х х = 2} =
5 1 5
1
5
Аналогично,
/>Ц = з} = А , Р{К = 6} = А
Таким образом, закон распределения случайной величины Y —Х\Хъ
имеет следующий вид:
Y
1
2
3
4
6
9
Р
2/21
5/21
5/21
2/21
5/21
2/21
Найдем теперь математические ожидания:
М Х х = М Х 2 = 1 • I + 2 • 1 + 3 • ± = 2,
М {Х Л } = 1 . | + 2 . | + 3 . | + 4 . | + 6 . А + 9 .
2__83
21
21'
_
Следовательно,
ОО
cov(Xh X 2) = М { Х хХ 2} - М { Х х} М { Х 2] = ££ - 2 • 2 =
1
2.
В условиях задачи 1 из данной группы людей случайно
отбираются 5 человек. Найти дисперсию суммарного дохода отобранных людей.
Р е ш е н и е . Пусть Х х, Х 2 , Х з , Х 4 ,Х^ — доходы отобранных
людей. Случайные величины Х х, Х 2 , Х з , Х 4 ,Х$ имеют одинаковое
распределение (см. решение предыдущей задачи), определяемое
таблицей
Р
1
2
3
1/3
1/3
1/3
здесь i = 1,2,3,4,5, причем соv{Xi,Xj) = —^
Поскольку
при любых i ф /.
DXi = MX? - (МХ х) 2 = | ,
то по формуле (2) получаем
D { X x + X 2 + X 3 + X 4 + X 5} = 5 - 1 + 5 - 4 - ( ~ ) = ^ .
3.
Пусть X и У — независимые случайные величины, имеющие плотности распределения /(х ) и g (x ) соответственно. Образуется двумерная случайная величина (Аь А2), где Х\ = min{A, У},
Х 2 = тах{А , У}. Найти плотность совместного распределения системы (A i,A 2).
Р е ш е н и е . Обозначим F(x) = Р { Х < х}, G(x) = P { Y < х}.
Тогда f(x) = F'(x), g(x) — G'(x). Для функции F(x i,x 2) распределения системы (Хх, Х 2) имеем:
F (xh х 2) = P{Ai < х и Х 2 < х 2} =
= P{min{A, У} < Х \ , тах { А , У} < х 2} —
= Р {( (Х < х х) + (У < х М Х < x 2)(Y < х 2)} =
= Р { ( Х < Х\)(Х < х2)(У < х 2) + (У < х х)(Х < x 2) ( Y < х 2)} =
= Р { ( Х < т т { х ь Х2})(У < х 2) + (У < min{xi,X2})(A < х 2)} =
= / 7(min{xi,X2})G(x2) + G{mvci{x\,x 2 })F{x2) —Р { Х < min{xi,X2}, У < min{xi,X2}, У < х 2, X < x 2J =
= F(min{x\,x 2 })G(x2) + G(min{xi,X2})F(x2) —P{A < min{xi,X2}, У < min{xi,X2}} =
при x x < x2;
\ F { x 2) G{ x 2) + G ( x 2) F { x 2) - F { x 2) G { x 2) = F { x 2) G ( x 2) при x\ > x 2.
_ ГF ( x i) G ( x 2) + G ( x i) P ( x 2)
- F(xi)G(xi)
Отсюда для плотности f ( x \ , x 2) совместного распределения системы (АьАг) получим
~ \ - d 2F(*i,x2) _ \f { x \) g { x 2) + g ( x x)f ( x2)
ПХ1,Х 2 )
дх[дх2
при
при
xi < х2;
Х1>Х2
VЛ
■4./Пусть X и У — независимые случайные величины, имеющие-распределение Пуассона с параметрами Хх и Ху соответственно. Доказать, что случайная величина Z — X + Y имеет распределение Пуассона. Выявить вид условного распределения случайной величины X при фиксированном значении случайной величины X + У.
Р е ш е н и е . По условию
Р { Х = k} =
P { Y = k} = ^ е ~ хУ,
где k = 0 , 1,2, . .. . Найдем вероятность
Р{ Х + Y = т} = Р{ Х = О, Y = т} + Р{ Х = 1, У = т - 1} + . ..
. . . + Р{ Х = т - 1, Y = 1} + Р{Х = т, Y = 0} =
т / \k
\ m~k
\
т \k\m-k
= V ' f — е ~ ^ х ■— l —
£-^\k\
(m —k)\
6=0 4
p-^y 1 = р-(Ь*+ \) V
J
х
у
£-^k\(m —k)\
7
_
6=0
1 w
I
= в-(Л*+А»)_1 У '
rn.
yk m_k =
ml
kl(m - k ) l
y
= e- ^ + A ,) 1 (л + A )m = (At + Xy)me~(\x+\y)
ml
y
ml
т. e. случайная величина X + Y распределена по закону Пуассона
с параметром Хх + Ху.
Найдем теперь условную вероятность
Р{ Х = к I л + г = ш) -
= >f + r - - ) =
yk
ym -k
_ Р{Х = k, Y = т - k} _ t \ e~Xx ' (■m - k )\e~Л
=
I
(А, + А ,) \_ ( а ,+ а ,)
ml
\k \m -k
Лх Лу
l
Й!(/Я —fe)! (Ад; + Ay)m
,
л
Лх
\ ^ /
\ [
\
Ay
\ m —k
^
mУАд; + Xy J \Ад; + Ху
т. е. условное распределение случайной величины X при фиксированном значении случайной величины X + Y = т есть биномиальное распределение с параметрами m и р = Ху/{Хх + А^).
(j^. Пусть X — центрированная (т. е. имеющая нулевое математическое ожидание) нормально распределенная случайная величина. Найти коэффициент корреляции случайных величин X
и Y — Х п, где п — натуральное.
Р е ш е н и е . По определению
Гху =
cov(X, Y)
Xй у
Д^ЗЛбб
cav(*, Y) = M { X Y } - M { X } M { Y } .
Поскольку по условию М {Х } = 0, то
Так как
fix) = - 7=L _ < r* 2/(2^2>
v 2 ttах
— плотность распределения случайной величины X , то
оо
М { Х п+х} =
[
J
—оо
dx.
V 27ГСГД;
Если я = 2&, то подынтегральная функция нечетна и М { Х п+1} = 0.
Пусть п = 2k — I. Тогда
ОО
[ —L - x 2ke - x2/ (2a^ dx,
J v 2 тгах
М { Х п+х} =
—оо
откуда, переходя к новой переменной интегрирования t = х / а Х1
получаем
оо
М { Х п+х} =
J
- ± = < j f t 2ke - t<ll 2 dt =
J lk
t 2k-xd{_ e^ ! ^ dt =
-
V 2 tt
.
Лk
= ^ L \ - t 2k- le- t 2/ 2
V 2n
+oo
+oo
{2 k - \ ) t 2k- 2 e - ? / 2 dt } =
+
2k
+?°
| ( 2 Л - 1 )t 2k~ 2 e~t2/ 2 dt.
Если обозначить
4-00
/ 2* =
y/2 n
то
-fo o
I2k = (2 k - I )
f
1 t 2k
2e
t2/ 2 dt _ (2 k _ l)/2£_2,
т. е.
I2k = (2k - 1)/2*_2 = (2Л - l)(2k - 3)/2fc-4 = • • •
.. . = ( 2 k - l)(2k - 3) . . . (2 k - (2 k - l))/0 =
+oo
1 е-*
_— I 2 d t = (2 k - 1)!!.
= (2 k - 1)!!
Таким образом, при n = 2k — \
M { X n+x} = M { X 2k} = a f ( 2 k - 1)!!.
(3)
Далее,
a 2 = D { Y } = D{Xn} = M { X 2n} - (M{Xn})2.
При n = 2k —1 имеем a 2 = M { X 4k~2}, откуда по аналогии с результатом (3)
a 2 = a 4k 2(Ak —3)!!,
или
ay = a 2k l y/(4k —3)!!.
Значит, при n = 2k — 1 (т. e. при нечетном ti)
a f ( 2 k - 1)!!
rxy =
Вчастности,
<TxO?~W№ - 3)!!
если п = 1, то
_
(2 k - 1)!!
>/(4* - 3)!!'
= 1; если п = 3, то гху =
3
Vl5’
VT5
еслип = 5, то г*,, = - ^ = . Если жеп = 2k (т.е. если/г четно), то
Зл/7
гху = 0 .
6 . Доказать, что коэффициент корреляции случайных величин по модулю не превосходит единицы.
Р е ш е н и е . Пусть г — коэффициент корреляции случайных
величин X и Y. Поскольку
D{X + Y} = DX + DY + 2rVDX\fDY,
TO
Пусть t =
D{X+Y}
VM Vd y
Vd
. Тогда
y
Vd x
Vd y
Vd ?
\[d x
откуда
1/
1\
г —~2 \
7/ w > 0 -
Из последнего условия следует, что г > —1, ибо mi n f i + l') = 2.
/>о \
г/
Аналогично,
D {X — Y} = DX + DY —2 r V M V D Y ,
D { X - Y } _ s/ В Х
s/ b x
Vby
| s /B Y
s/ b y
2r
s/ d x
Если t = —y = , TO
s /B Y
W> 0
t + - —2 r >
0
,
откуда
r < - 2 (t +
-t )
voo.
Из последнего условия следует, что г < 1. Таким образом, \r\ < 1.
(j(. Иусть X и Y — независимые случайные величины, равномерно распределенные на отрезках [а\,Ь\\ и [02,^ 2] соответственно. Найти плотность распределения случайной величины
Z = X+Y.
Р е ш е н и е . Решим сначала следующую общую задачу: найти
плотность распределения fz(z) случайной величины Z = X + Y,
если случайные величины X и Y независимы и имеют плотности распределений fx(x) и f Y{y) соответственно. Рассмотрим приближение непрерывной случайной величины X дискретной слу^
чайной величиной X подобно тому, как это было сделано в §6
при выводе формулы для математического ожидания непрерывной
случайной величины. Для функции распределения случайной величины Z можем написать
Fz { z ) = P { X + Y < z} и P { X + Y < z } = J 2 P { X = x h Y < z - x t} =
i
= J2 p {X =
Xi}P{Y
< z - Xi} = J
i
2
f x ( x i ) A x i F Y ( z - Xi).
i
В пределе при уменьшении шага дискретизации последняя сумма
будет стремиться к интегралу
ь
\ f x { x ) F Y{ z - x)d x,
где (а, Ъ) — промежуток изменения случайной величины X. Если X может принимать значения от —оо до +оо, то интеграл будет
несобственным и в общем случае
+00
F z ( z ) = [ fx (x)FY( z - x ) d x ,
^
^
!
&
откуда, дифференцируя обе части равенства по z, получаем
+оо
fz{z)=
J f x ( x ) f y ( z - x)dx.
—оо
Следовательно, в нашем случае равномерных распределений для
X и Y имеем:
<4>
а,
где
^
fy (z — х) = { b2 - a
0
2
При
0,2
при
z —х $ [«2, &г]-
< z — X < Ь2 ,
Вычислим интеграл (4). Условие а.2 < z — х < &2 эквивалентно
условию
Z — b2 < х < Z — 0,2-
В зависимости от различных значений переменной z (которая при
вычислении интеграла (4) выступает в роли параметра) результат
вычисления (4) будет следующим.
При
Z
ах
Ьх
1------------------1---- 1-----------------------1----------------------------►X'
- Ь2
Z - <22
т. е. при z — а,2 < а ь или z < а\ + Я2, будет fz(z) = 0.
При
ах
Ьх
------------------- ,------ 1------ 1------------- — I--------------------------- ►х ^
Z-b<i
Z - й2
т. е. при одновременном выполнении условий
ах < z — а 2 < b\,
z —Й2 < а\,
или
a i + c i 2 < z < a 2 + bi,
z < a \ + b2
(положим для определенности Ь\ — а\ > &2 —0,2 , тогда и для z
получаем условие а\ + 02 < z < а\ + 62). будет
г-а 2
1
а\
Z — й \ — 0,2
,
Ь2 —а 2
ах =
(bi -ci)(&2 - e 2)'
«1
При
ai
Z-
62
z - Д2
т. е. при одновременном выполнении условий
z - а 2 < b\,
z - Ь2 > а\,
или а\ + £?2 < z < й2 + Ь\, для функции fz(z) получим
г-аг
fz(z)
2-Й2
1
Ь\ —а\
1
dx
Ь2 —а2
1
Ъ\ —а\
При
а\
z-b
z - а2
2
т. е. при одновременном выполнении условий
z-a
2
> b \,
z-b
2
< b i,
или 02 + b\ < z < Ь\ + &2 (условие z — b2 > a \ при этом выполняется автоматически), для функции fz(z) получим
1
bi - а \
fz(z) =
1 dx=
Ь' + Ь2~ г
Ь2 —а2
(bi —a\){b2 - а2)"
Z—b2
Наконец, при
а1
z —b2
z —а2
т. е. при z — Ь2 > Ь\, или z > b\ + 62. будет fz{z) = 0 .
Таким образом,
'0
z —а\ —а,2
{Ь\ - щ)(Ь2 - а2)
1
Ь\ —а\
bi + b2 - z
(Ь\ - а\)(Ь2 - а2)
0
при
z < а\ + а 2,
при
CL\ +0,2
при
a\ + b2 < z < а 2 + &ь
при
CL2 +
при
г > Ь \
< Z
< й\ + Ь2.
b \ < г < Ь\ + Ь2 ,
+
Ь2 .
иметь следующий вид (рис. 6).
Рис. 6
С
8.^Плотность совместного распределения системы (X , Y) имеет вйд
fix, у) =
\А(х + у)
при
О
0 < х < 1, 0 < у < 1;
в противном случае.
Найти Р{Х + Y > 1}, MX, DX и гху. 7
Р е ш е н и е . Найдем сначала константу А из условия нормировки:
+ о о -f-OO
1=
1
1
J |
f(x ,y )d x d y = А ^ dy^(x + y ) d x =
— ОО — ОО
о
о
1
=А
.
о
((£+yx)Vyy=A\ih+y)iy=Ai$
+
о
= А,
т. е. А = 1. Далее (см. рис. 7),
l
l
Р { Х + У > 1} = | | f(x, у) dx dy = | dx | (x + y) dy =
о
i—x
ХУ + Т
У
dx =
x + 1 - x(l - x) - ^ ^
) dx =
y = l-x
C
M |CO
y=i
Чтобы найти M X и DX, найдем сначала плотность /х(х) распределения случайной величины X:
+00
fx(x)= | f(x,y)dy =
(x + y ) d y = x + ^
— ОО
при
х€[0,1];
при
х ^ [0,1].
Следовательно,
+00
МХ =
xfx(x) dx =
x(x+i)dx=h
■
о
+о о
DX = M X 2 - (MX ) 2 = I x 2f x ( x ) d x - ( M X ) 2 =
—oo
2
2(*+0 Л~ ® 2=
jn_
144'
Из симметрии задачи следует, что M Y = MX, DY — DX.
„ cov(X,Y) п
Найдем теперь гху = ------------ . Поскольку
^ XСГу
cov(X, Y) = M { X Y } - M { X } M { Y },
то нужно найти
-)-оо -j-oo
M{XY} = |
1
xyf(x,y)dxdy =
1
dx xy(x + y )d y =
о
о
y= 1
4
+4
y=0
0
Значит,
_1_
IT'
9.
Система случайных величин X, Y распределена по нормальному закону с плотностью
1{х’ у) = т л ехр { ~
- i y2 - х у ~ * ~ 1%- f )
Найти математические ожидания тх,ту, среднеквадратичные отклонения <jXl(jy и коэффициент корреляции г.
Р е ш е н и е . Плотность двумерного нормального распределения имеет вид
/ ( Х
, у
)
=
X
1
2 ттахаул/\
с::р f
1
- г:
1
2(1 —г2) V
~
m **2
2г
~
~
\ ^ ~
^]
)У
Обозначим
А =
1
2(1- r V 2’
В =
2(1 - r 2)<rf
С=
(1 - Г2)<ТхСГ„
Тогда
1 2.
7 2
10
^25
- к* - ЪУ - ху - X - \Ъу - — =
2
2
2
2
d /„
_ \2 + С(х - пгх)(у - ту),
-Л(х - тху - В
(у - ШуУ
откуда методом неопределенных коэффициентов (т.е. приравнивая коэффициенты при одинаковых степенях х и у и при ху слева
и справа) получим:
А = 1,
В=1
С
1.
' 2А т х —Сту = —1,
2Вту — Стх — —13,
25
2
—A m-хi — Bmi
‘■’ " ' у +
' Стхт„ =
1 и ту = —2.
Решая последнюю систему, найдем тх
Далее,
.2
ау
А
1
п = - a1t = 7 »I
в
/?
0ТКУДа
= v 7cTy
Решая теперь систему
1
2(1- г 2)а,2
г
( 1-Г )<7хОу
2’
= -1 ,
„ <7* = V%V,
получим:
/7
ст* - \ / б ’
1
1
л/7'
Г_
В заключение проверим совпадение коэффициента перед экспонентой:
1
_
1
_
1
_ \/б _
V3
10. Найти плотность распределения случайной величины
Y=
Xi
Х1+ Х 2’
если Х\ и Х 2 — независимые и равномерно распределенные на
отрезке [0,1] случайные величины.
Р е ш е н и е . Найдем сначала функцию распределения F(y)
случайной величины Y. Ясно, что Р{0 < Y < 1} = 1 и
F{y) =
1
при
у > 1;
0
при
у < 0.
Рассмотрим значения у € (0,1). Тогда
F{y) = P { Y < у} = p { j ^ Y
2
< у} =
< У&1 + х 2 )} =
= я д а 1 - у) < Ух 2} = р { х 2 > ^ * i } .
Пусть f{ x \, x2) — плотность совместного распределения системы
Х \ , Х 2. Тогда, как следует из условия,
1,
0,
f( x h x 2) =
если х\ € [0,1],
в противном случае.
[0,1];
Пусть сначала у е (0,1/2]. Тогда (1 - у ) / у изменяется от +оо
до 1 и (см. рис. 8)
Р[х2
>
=
^ f ( x b x 2) d x xd x 2 =
G
1
у/( 1-у)
=
J
dxi
|
y/Q-v)
( l - -—
f ( x u x 2) d x 2 =
Xl(l-y)/y
=
У-x^j dxi
о
2\\X\=y/(\-y)
V
Рис. 8
у
2
)L
i=
„=0
у
= 2J T T Y
Пусть теперь у е [1/2,1). Тогда (1 —у ) / у изменяется в пределах от 1 до 0 и (см. рис. 9)
1
я |^ 2 >
1
J
- Х \ ^ = ^ f ( X \ , X 2)dX\dX2 = ^ d X \
у
о
о
f ( x i , x 2) d x 2 =
^
= V i - l z ± x ^ iXi = ( X l - ^ A Y ' - ' =
Л
у
J
\
у
2 / Х1=0
о
=
2У
Таким образом,
F(y) = <
0
при
У < 0;
У
2(1 —у)
при
0
при
\ < у < 1;
при
г/ >1.
(З у -1 )
2У
<1
< у < £,
Следовательно,
II
'о
1
2 (1 - У?
= <
1
2у 2
к0
при
г/ < 0;
при
0 < у < 1;
при
1 < г/ < 1;
при
у > 1.
2У
§ 8. Закон больших чисел
и центральная предельная теорема
Пусть Y — произвольная случайная величина, такая, что существует математическое ожидание МЦУ!*}, где k > 0. Тогда для
любого фиксированного числа е > 0 имеет место неравенство
Чебышёва:
■
Я { | У | > £} < М ^ 1 .
(1)
Покажем справедливость этого неравенства для случая, когда Y — непрерывная случайная величина с плотностью распределения f(y). В этом случае
ОО
М { |У |* } = J
ОО
—£
\y\kf ( y ) d y >
— ОО
|
\y\kK y ) d y + \ \ y \ kf ( y ) d y >
— ОО
ОО
—£
> |
£
£kf{y) d y
— OO
+ J
£kf(y) d y =
£
—£
= £k
( J f(y) dy +
— OO
OO
| f{y) dy) = ekP {| Y\ > e},
£
откуда и следует нужное неравенство.
_
Рассмотрим теперь один частный случай неравенства (1), а именно: применим его к случайной величине Y = X — тх, где X —
некоторая случайная величина, тх = M X — ее математическое
ожидание, причем положим k = 2. Получим:
P { \ X - m x\ > e } < ™ ,
£
откуда
ПУ
Р{|Х —тх \ < е} > 1 — -у-,
где DX — дисперсия случайной величины Х \ Пусть теперь е = За*,"
где ах = у/DX — среднеквадратичное отклонение случайной величины X. Тогда
Р{\Х - тх\ < 3»,} > 1 - ^ 5
=
или
Р{тх - Зах < X < тх + Зах] > - ,
т. е. вероятность того, что значение случайной величины отличается от ее математического ожидания менее, чем на три среднеквадратичных отклонения, не меньше 8/9.
Следует отметить, что для многих распределений случайных
величин эта вероятность значительно ближе к единице, чем 8/9.
ЛЗапример, для нормального распределения она равна 0,997__
Поэтому на практике в таких случаях диапазон возможных значений изучаемой случайной величины X ограничивают интервалом (тх — Зах, тх + Зох), называя это упрощение правилом трех
сигм.
S- Теорема 1 (теорема Чебышёва). Пусть имеется бесконечная
последовательность Х\ ,Х 2 , . . . независимых случайных величин, таких, что
/
MXi = М Х 2 = .. . = т;
DX\ < с, DX 2 < с, / . . . ,
где с > 0 и т — постоянные. Тогда для любого числа е > 0
Хх+Х2 + ...Х п
—т < е
lim Р{
п-+ОО
Д о к а з а т е л ь с т в о . Применим неравенство Чебышёва (1)
к случайной величине
Х\ + Х 2 + . . . Хп
Согласно этому неравенству при k — 2 имеем
откуда
Но
M{S„} = т,
D{5„} = -L Y ,D { X i } < Ц = ~,
i=1
так что
—т < е
откуда переходом к пределу при п —> оо и получаем требуемый
результат.
Отметим, что теорема Чебышёва оправдывает рекомендуемый
в практической деятельности способ получения более точных результатов измерений: одна и та же величина измеряется многократно, и в качестве ее значения берется среднее арифметическое
полученных результатов измерений.
Непосредственным следствием теоремы Чебышёва является *
Теорема 2 (теорема Бернулли). Пусть k — число успехов
в серии из п независимых испытаний Бернулли, р — вероятность успеха в одном испытании. Тогда для любого е > О
П т Р { | - —р < e l = 1.
п- too 11я
J
Д о к а з а т е л ь с т в о следует из теоремы Чебышёва, если заметить, что
k = X 1 + X 2 + . . . X n,
где случайная величина X,- — число наступлений успехов в г-м
испытании. Ясно, что все X,-, / = 1,2, . . . , п , имеют одинаковое
распределение, определяемое таблицей
Xi
1
0
р
р
1- р
При этом MXi = р, DXi = р( 1 —р), так что все условия теоремы
Чебышёва применительно к последовательности случайных величин Х \ , Х 2, ■. . выполняются.
Теорему Бернулли можно интерпретировать как факт, подтверждающий непротиворечивость строгого аксиоматического
подхода к определению вероятности (см. § 2) по отношению к экспериментальному статистическому подходу, согласно которому
вероятность Р{А} события А определяется как предел
п—
П
’
где п — общее число испытаний, k(n) — число испытаний, приведших к событию А.
Теорема 3 (центральная предельная теорема в форме Ляпунова). Пусть последовательность Х \, Х2, . . . независимых случайных величин удовлетворяет условию Ляпунова
где dt = D{Xi}, hi = М { \Xt - М Х ^ } . Тогда
0
lim Р {а < Х п < /3} = [ —
J V 2^
л-оо 1 -
dx,
а
где
Ъ _ Х ' „ - М { \ Г'}
_ v , v. ,
v,
Другими словами, центрированная и нормированная сумма
Х \ + Х ^ + . . . + Х п при п —►оо ведет себя как нормально распределенная случайная величина с нулевым математическим ожиданием и единичной дисперсией.
Не приводя доказательства теоремы 3, покажем, что услбвие этой теоремы выполняется, в частности, в том случае, когда
случайные величины Xu i = 1, 2, . . . , имеют один и тот же закон
распределения. При этом hi = h, d{ = d для любого i = 1, 2 , . . . , и
П
J 2 hi
\
—^
,\Э/2
( z ^ ‘7
,
I
r
(nd) /
= ~ ш ' ~7=
d ^ Vn
О ПРИ п
оо-
i= 1
В заключение, в качестве одного из приложений теоремы 3,
покажем, как из нее может быть получена уже упоминавшаяся
в курсе (см. §4) интегральная теорема Муавра-Лапласа.
Пусть k — число успехов в серии из п независимых испытаний
в схеме Бернулли, р — вероятность успеха в одном испытании.
Тогда
к = Хл + Х 2 + . . . + * „ ,
где Х \ , Х 2 , . . . , Х п — независимые случайные величины, имеющие
одинаковый закон распределения
Xi
1 0
р
р
я
где q = 1 —р. Поскольку M { k} = пр, D{k} = npq, то по теореме 3
при больших п
Р
Далее, неравенство
a < k- Z M
Фт
эквивалентно неравенству
< 0
k \ < k < k 2,
где
k\ = пр + a^/npq,
&2 = пр + (Зл/npq.
Поэтому из (2) получаем
(k2- n p ) / y / n p q
- j = e x / 2 d x,
p { k 1 < k < k^\
I
/
V2n
(k i-n p )/y /n p q
j
ИЛИ
X
где Ф(х) =
—\=e~ t2№ dt — функция Лапласа.
J v2n
0
—!
Задачи
1.
Проводится серия из п независимых испытаний с вероятностью успеха р в каждом испытании. Используя неравенство
Чебышёва, оценить вероятность того, что число X успехов будет
заключено в пределах от k\ до k 2, где (&i + k2)/2 = MX.
Р е ш е н и е . Воспользуемся неравенством Чебышёва в форме
ПУ
Р {\Х -М Х \ <е} > 1 - = £ .
£
В нашем случае M X = пр, DX = пра. Обозначим е — k 2 — M X =
= M X — k \ . Тогда
P { h < X < k 2} = P { M X - e < X < M X + e} =
= Р { \ Х - М Х \ < е } > \ - ^ = \ --------- ^
11
'
е2
т - к х) / 2 Г
т. е.
/>{*, < X < *2} > 1 -
№ - К\)
,.
Рассмотрим примеры.
а) р = 1/2, я = 100, k\ = 40, k<i — 60:
Р{40 < X < 60} > 1 -
4 100 i i
(60 - 40)2
з.
4’
б) р — 1/4, п = 800, &i = 150, &2 = 250:
/>{150 < X < 250} > 1
4 ' 8 0 0 - I | _ 47
(250 —150)2
50*
2.
Доказать, что если случайная величина X такова, что М { е аХ}
существует (а > 0 — постоянная), то для любого е > 0
Р е ш е н и е . Проведем доказательство для случая непрерывной случайной величины, имеющей плотность распределения f{x).
Имеем
+ 00
+00
+оо
М { е аХ} =
eaxf(x) dx >
eaxf(x) dx >
easf{x) dx =
+00
f{x) dx = eaeP{ X > e.},
т. e.
M { e aX} > eaeP{ X > £ },
откуда и следует требуемое неравенство.
3.
Пусть ф{х) > 0 — неубывающая функция. Доказать, что
если существует М{ф(\Х — МХ\)}, то
Р{\Х-М Х\ > е }<
М{ф{\Х-МХ\)}
ф{е)
Р е ш е н и е . Проведем доказательство для случая непрерывной случайной величины, имеющей плотность /(х). Имеем
+оо
М { ф ( \ Х - М Х \ ) } = | ф(\х - MX\)f{x) dx =
— ОО
{переходим к новой переменной интегрирования t = х —MX}
+оо
—Е
+00
> [ <t>(\t\)f(t + M X ) d t + f <f>(\t\)f(t + M X ) d t >
— ОО
£
{пользуемся неубывающим характером функции ф(х) > 0}
+00
— £
> | <j>(e)f(t + M X ) d t + | <f>(e)f(t + M X ) d t =
— ОО
£
{переходим к переменной интегрирования х = t + MX}
-(-оо
M X —£
=
<f>(e)f(x)dx+
4>{e)f{x)dx
=
МХ+£
-О О
+оо
М Х —£
= ф(е) ^
f{x) dx +
OO
f(x) d x j =
A4X-\-£
= ф(е)(P{X < M X - e } + P { X > M X + e } ) = ф{е)Р{\Х-МХ\ > е},
т. е. установлено, что
М{ф(\Х - M X |)} > ф(е)Р{\Х - M X | > е},
откуда и следует нуж ное неравенство.
4.
П оследовательность независим ы х случайны х величин Х\,
Х 2 , . . . , Х п, . . . задан а следую щ им законом распределения:
Хп —па
Р 1/2"
0
па
1 - 1/2"-1 1/2"
Здесь а > 0 — постоянная. Выяснить, применима ли к данной
последовательности теорема Чебышёва.
Р е ш е н и е . Заметим сначала, что М Х п = 0 для любого п =
= 1 , 2 , . . . . Теорема Чебышёва будет применима, если найдется постоянная С, такая, что DXn < С для любого п = 1,2,. .. .
Имеем
DXn = MX* - (МХп ) 2 = MX* = ^ а 2.
Исследуем выражение я 2/2 " -1 , я = 1 ,2 ,
С этой целью рассмотрим функцию f(x) = х 2 / 2 Х~Х, х > 1. Эта функция непрерывна
в [1, -|-оо) и имеет конечный предел на +оо:
lim f{x) = 0.
X —++СХЭ
Следовательно, она ограничена в [1,+оо), т. е. существует постоянная В, такая, что для любого х € [1,+оо) будет /(х) < В.
Поэтому
я2
DXn =
—В ® 2 для ЛК)бого я = 1, 2, . . . ,
так что за постоянную С можно принять произведение В с ? . Таким
обоатом, теорема Чебышёва применима.
/ 5. Пользуясь центральной предельной теоремой, оценить,
сколько необходимо произвести бросаний «правильной» игральной кости, для того чтобы с вероятностью не менее 3 /4 сумма
выпавших очков превысила 780.
Р е ш е н и е . Пусть случайная величина X t — число очков, выпавшее при г-м бросании игральной кости, i — 1,2, . . . , я . Тогда
закон распределения для Xi дается таблицей
Xi
p
1
2
3
4
5
6
1/6
1/6
1/6
1/6
1/6
1/6
так что MXi = 7-, DXi =
М{Хх + Х 2 + . . . + Х п} = М Х 1 + М Х 2 + . . . + М Х п = п - ^ ,
а в силу независимости случайных величин X i , X 2, .. . , Х п
D { X x + X 2 + . . . + X n} = D X l + D X 2 + . . . + D X n = n - ^ .
В соответствии с центральной предельной теоремой при больших я
+00
Г 1 _,V2
J X l + . . . + X . - M {X l + . . . + X , } ^
I
y/D{X, + . . . + X „ }
I
I
-J b :
A
И ЛИ
+oo
P \ X\ + . •. + X n > A \ j — n +
e tZ/ 2 d t
Искомые значения п найдутся из условий
= 780,
<
+оо
[
J
I А
= e-^dt
~ 4'
V2*
4
При граничном значении
- f ОО
3
Г
1
А
по таблицам функции Лапласа находим А — —0,675, после чего,
решая уравнение
определяем п (округляя до ближайшего целого справа): п — 228.
6.
Найти пределы, в которых с вероятностью, большей 0,99,
будет находиться суммарное число выпавших очков при 1000кратном бросании «правильной» игральной кости.
Р е ш е н и е . Первый способ. Решим сначала задачу с помощью
неравенства Чебышёва. Пусть случайная величина Х х — число очков, выпавшее при i-м бросании игральной кости, i = 1,2, ... ,п.
Тогда (см. решение задачи 5)
MXi =
7
М { Х х + Х 2 + . . . + Х п} = ' - п ,
DXi = g ,
ЧЧ
D { X x + Х 2 + . . . + Х п} = ^ п .
Обозначим S n = Х\ + Х 2 + . . . + Х п. По неравенству Чебышёва
Р{|5 я - М 5 „ | < в } > 1 Пусть 1 - ^
£
DS,*П
£'
= 0,99. Тогда
VDS,
У т Г 1000 = 5 4 0 ,0 6 ... .
7
Поскольку M S n = 2 ’ Ю00 = 3500, то получаем
/>{3500 - 540 < S n < 3500 + 540} > 0,99,
Второй способ. Решим теперь задачу, опираясь на центральную предельную теорему. Согласно этой теореме при больших п
ь
■MSn
’flli - л
< el и
J
J
L=e~t2/ 2dt = 2Ф(е),
у
27Г
Z
где Ф(г) =
—= e ~ t2/ 2dt — функция Лапласа. При 2Ф(е) = 0,99
J у27Г
о
получаем: е — 2,58,
^D Sn .е =
. Ю00 • 2,58 = 139,33
в результате чего имеем
Р{3500 - 140 < S n < 3500 + 140} > 0,99.
Как видно, центральная предельная теорема дает существенно более узкий интервал для S n, т. е. позволяет решить задачу гораздо
точнее.
7.
Книга объемом 500 страниц содержит 50 опечаток. Оценить вероятность того, что на случайно выбранной странице имеется не менее трех опечаток. При решении задачи использовать:
а) пуассоновское приближение, б) нормальное приближение,
в) формулу Бернулли.
Р е ш е н и е . Можно предложить следующую интерпретацию
обнаружения опечаток. Зафиксируем случайно выбранную страницу и будем «вбрасывать» опечатки одну за другой в книгу,
т. е. будет проводится серия из п = 50 независимых испытаний
Бернулли, где под успехом будет пониматься попадание вбрасываемой опечатки на заранее выбранную страницу. Ясно, что вероятность успеха р в каждом испытании равна р = 1/500. Пусть X —
число успехов в этих п испытаниях. Тогда искомая вероятность
Р {Х > 3} = 1 - Р{Х = 0} - Р{Х = 1} - Р{ Х = 2}.
По формуле Пуассона
получим
Р{ Х > 3} = 1 - е-0,1
^
= 0 ,0 0 0 1 5 5 ....
Воспользуемся теперь нормальным приближением, т. е. центральной предельной теоремой. В данном случае она представляет собой интегральную теорему Муавра-Лапласа, согласно которой имеем:
Р{Х > 3} = Р{3 <
< 50} = ф (
f 0 ~ nP
\ \ / п р ( 1 - p)J
Ъ~ пР Л =
\ у / п р ( \ - p)J
В заключение, используя формулу Бернулли
P{ X = k} = Cknpk{ \ - p ) n- \
получим точный результат:
Р{Х > 3} = 1 - Р{Х = 0} - Р{Х = 1} - Р{Х = 2} =
= 0 ,0 0 0 1 4 6 ....
8.
В тесто для выпечки булок с изюмом замешано п изюмин.
Всего из данного теста выпечено k булок. Оценить вероятность
того, что в случайно выбранной булке число изюмин находится
в пределах от а до Ь.
Р е ш е н и е . Будем считать, что каждая изюмина с одинаковой
вероятностью может оказаться в любом фрагменте теста независимо от того, куда попали остальные изюмины. Тогда случайная
величина X — число изюмин, попавших в случайно выбранную
булку, может быть описана биномиальным распределением с параметрами п (число испытаний) и \ / k (вероятность успеха в одном испытании):
где т = 1,2, . . . , п. Поэтому
.^ .
/ 1 \ т /
Р{а<Х< Ь} = - £ с j ( i )
( \ п -т
(l-I)
•
т —а
Поскольку M X = 7 , DX = П^
<7* =
^— —, то при больk
k
k
ших п интегральная теорема М уавра-Лапласа дает следующее
приближение для искомой вероятности:
Р{а < X < Ь} и
9.
В поселке N жителей, каждый из которых в среднем п раз
в месяц ездит в город, выбирая дни поездки независимо от остальных жителей. Поезд из поселка в город идет один раз в сутки.
Какова должна быть вместимость поезда, для того чтобы он переполнился с вероятностью, не превышающей заданного числа /??
Р е ш е н и е . Примем для простоты, что в месяце 30 дней. Если
житель поселка в среднем п раз в месяц ездит в город, то вероятность того, что в случайно выбранный день этот житель поедет
в город, равна п / 30. Случайная величина X — число жителей
поселка, отправившихся в город в один и тот же день, описывается биномиальным распределением с параметрами N (число
испытаний) и п/ 30 (вероятность успеха в одном испытании):
/Ч* = »} = с * ( | Л . - £ ) - .
где т = 1,2, . . . ,N. Тогда N* — искомая вместимость поезда —
определится из условия
Р {Х > N*} < (3,
или
1 - Р{0 < X < N*} < (3,
Р{0 < Х < N*} > 1 - 13.
Минимальное N*, удовлетворяющее этому условию, определится
из равенства
Если поселок большой и N велико, то вероятность в левой части
можно оценить по интегральной теореме Муавра-Лапласа. Поскольку
я(30 - n)N
at V
nN
г\ V" nN (,
п\
= зо' ш = з о { ‘ ~ з д ) =
зо2
уГох _ V
’““
а%
~ n)N
30
то
ПГЛ/ V / A r * !
Х>1М* ~ МХ \
Л /0 - MX
Р {о < X < N } и Ф (
- Ф
/
®х
—Ф
где
Ф(г)
—)= е t2!2dt
у/Ъг
V
<?х
nN
\
ж( 30 N* - nN
V у/п (30 -
у/п (30 - n ) N j
—
функция
Лапласа.
n)N
Так
как
_/
nN
\
1
» 1, то Ф( ,
= I= - и
х/«(30 - «)iV
’
\y/n(30-n)N j 2
nN
1
ф / ЗОЛГ-яЛП
2
\^n(30-n)N /
ф /^ -3 0 Л ^ _ \ = 1_
\^/n(30-n)N j
2
Полученное равенство при заданных параметрах п, N и (3 по табл и прм з начений функции Лапласа позволяет определить число 7V*.
Г10. Йеобходимо сложить миллион чисел, округленных с точностью до пятого десятичного знака. В предположении, что ошибки округления всех чисел взаимно независимы и имеют равномерное распределение в соответствующем интервале, найти пределы, в которых с вероятностью 0,95 находится суммарная ошибка
округления.
Р е ш е н и е . Пусть Xi — ошибка округления г-го числа. Тогда
суммарная ошибка округления
Х = Х1+ Х 2 + . . . + Х „ ,
где п = 106. По условию случайные величины Xi независимы
и имеют одинаковое распределение — равномерное распределение
на отрезке [—5 • 10_6, 5 • 10_6], так что
MXi = 0,
Ю-ю
DXi = ^ - ~ ,
ALY = 0,
10~4
DX — —гн- ,
Ю-2
<Jx =
В соответствии с центральной предельной теоремой
х -м х
<Р
1 -;2
у/ 2 тг
откуда
Pi - S <
где Ф(г) =
V 2n
X
<s
10“ 2/2%/3
2Ф(6),
е /2//2 dt — функция Лапласа. Если 2Ф(<5) = 0,95,
то по таблицам значений функции Лапласа находим S = 1,96.
Таким образом,
Pi
I
то-2
ю -2
. 1,96 < х < ^ - 1,96 } = 0,95,
2^3
’ ~
~ 2V3
или
Р { - 0,0057 < X < 0,0057} = 0,95.
§ 9. Исходные фундаментальные определения,
понятия и результаты
1.
Рассмотрим случайный эксперимент Е, не интересуясь его
конкретным видом. Событие Л, связанное с Е, будем называть
наблюдаемым, если в результате Е всегда можно однозначно сказать, произошло А или нет. Событие, происходящее всякий раз
при проведении эксперимента, будем называть достоверным событием и обозначать О; событие, которое никогда не происходит
при проведении эксперимента Е, будем называть невозможным
событием и обозначать 0. События Q и 0 считаются наблюдаемыми. Пусть А и В — некоторые наблюдаемые события, связанные
с проведением эксперимента Е. Определим:
1) дополнительное событие к А, обозначаемое Л и состоящее
в том, что А не происходит;
2) сумму, или объединение А и В, обозначаемую А + В или
Л U В и состоящую в том, что происходит по крайней мере одно
из событий Л или В;
3) произведение, или пересечение А и В, обозначаемое АВ
или Л П В и состоящее в том, что происходят оба события Л и В.
Будем считать, что события Л, Л + В и Л В, как Л и В, наблюдаемы. Тогда семейство всех наблюдаемых событий, связанных с Е,
образует поле событий То, т. е. класс событий, включающий достоверное событие Q и замкнутый относительно трех только что
определенных операций (замкнутость, по определению, означает,
что если Л, В € То, т о Л, В, Л + В, А В € То). Непосредственно из
определения следует, что события, принадлежащие полю То, удовлетворяют соотношениям:
А+А=АА=А,
Л + В = В + Л,
(А + В) + С = А + (В + С),
А В = ВЛ, (Л В )С -Л (В С ), А(В + С ) = А В + АС, Л + Л = П ,
ЛЛ = 0, Л -}- Г2 = П, ЛГ2 —Л, Л Т 0 —Л, Л0 — 0.
В соответствии с центральной предельной теоремой
/з
п /
^ Х - М Х
Р<а<
I
Ox
\
Г
J
J V2tt
1
< (3> ~ \ —F=e
^212 j .
1 1* dt,
откуда
2
где Ф(г) -
1 -t*
e 1 ^ dt — функция Лапласа. Если 2Ф(<5) = 0,95,
y/bi
то по таблицам значений функции Лапласа находим S = 1,96.
Таким образом,
10~2
10-2
• 1,96 < X <
• 1-96 } = 0,95,
2^3
’ ~
~ 2V3
или
Р { —0,0057 < X < 0,0057} = 0,95.
§ 9. Исходные фундаментальные определения,
понятия и результаты
1.
Рассмотрим случайный эксперимент Е, не интересуясь его
конкретным видом. Событие Л, связанное с Е, будем называть
наблюдаемым, если в результате Е всегда можно однозначно сказать, произошло А или нет. Событие, происходящее всякий раз
при проведении эксперимента, будем называть достоверным событием и обозначать Q; событие, которое никогда не происходит
при проведении эксперимента Е, будем называть невозможным
событием и обозначать 0. События П и 0 считаются наблюдаемыми. Пусть А и В — некоторые наблюдаемые события, связанные
с проведением эксперимента Е. Определим:
1) дополнительное событие к А, обозначаемое Л и состоящее
в том, что А не происходит;
2) сумму, или объединение А и В, обозначаемую А + В или
Л U В и состоящую в том, что происходит по крайней мере одно
из событий Л или В;
3) произведение, или пересечение Л и В, обозначаемое ЛВ
или Л П В и состоящее в том, что происходят оба события Л и В.
Будем считать, что события Л, Л + В и ЛВ, как Л и В, наблюдаемы. Тогда семейство всех наблюдаемых событий, связанных с Е,
образует поле событий F q , т. е. класс событий, включающий достоверное событие Q и замкнутый относительно трех только что
определенных операций (замкнутость, по определению, означает,
что если Л ,В е T q , т о Л, В, Л + В , Л В е F q ) . Непосредственно из
определения следует, что события, принадлежащие полю Тр, удовлетворяют соотношениям:
Л+Л=ЛЛ=Л,
Л + В = В + Л,
(А + В) + С = А + (В + С),
А В — ВА, (АВ)С = Л (ВС), Л(В + С) = Л В + ЛС, А + А = П,
А А = 0, Л + П = П, ЛП = Л, Л + 0 = Л, Л0 = 0.
Пусть теперь А', В' я в л я ю т с я множествами точек ш произвольного пространства VI'. В элементарной теории множеств определяются множества А', В', А ' + В ' , А ' В ' . Из этих определений (которые предполагаются читателю известными) легко следует, что
все приведенные выше соотношения для событий остаются справедливыми и тогда, когда А, В , . . . обозначают множества. Аналогично полем множеств в П' называется семейство множеств,
включающее все пространство VI' и замкнутое относительно операций А7, А' + В', А'В'.
Оказывается, имеет место следующий результат: для любого
поля То событий, удовлетворяющих перечисленным выше соотношениям, можно найти некоторое пространство VI' точек и
и такое поле Tq од-множеств, что между событиями А в То
и множествами А' в T'Q будет существовать взаимно однозначное соответствие, причем если событие А соответствует множеству А ' , событие В — множеству В', то событие А будет
соответствовать множеству А', событие А + В — множеству
А' + В ' , событие А В — множеству А'В'. При этом точки од будут
соответствовать некоторым элементарным событиям, которые
могут или не могут наблюдаться в отдельности (т. е. могут входить, а могут не входить в То по отдельности), а достоверному
и невозможному событиям будут соответствовать все пространство Vt' и пустое множество, для обозначения которого так же,
как и для обозначения невозможного события, используется
символ 0.
Сформулированный результат позволяет для анализа полей
событий использовать аппарат теории множеств. В дальнейшем
штрихи будут опускаться, и для событий и ад-множеств будут
употребляться одни и те же обозначения То, А, В , . . . . Множество в То будет называться наблюдаемым событием, или адмножеством, VI будет рассматриваться как достоверное событие,
или как все пространство, и т. д.
Предположим теперь, что каждому событию А поля наблюдаемых событий То, отвечающего случайному эксперименту Е, поставлено в соответствие определенное число Ро{А}, называемое
вероятностью события А. Считаем, что Ро{А} есть некоторая
функция, определенная для всех событий или множеств А € То,
удовлетворяющая соотношениям
О < Ро{А} < 1,
Р о{0} = 0,
P 0 {Vl} = 1
и обладающая свойством конечной аддитивности: если А = А\ + . ..
. . . + А п, где At е То, i = 1 , . . . , п (а значит, и Л G То), A/Ak = 0
для / ф k, то
Ро{А} = Р 0 { А 1} + . .. + Р 0 {А я}:Утверждение о существовании функции Ро{А} с описанными
свойствами принимается как аксиома, т. е. как утверждение, не
требующее доказательства.
Пусть теперь At, А ^ , . . . — произвольная счетная бесконечная
последовательность множеств из То- Множества вида А 1 + А 2 + . . .
и А \ А ч - . . , т.е. являющиеся счетными бесконечными объединениями и пересечениями множеств из То, могут (в отличие
от конечных объединений и пересечений), вообще говоря, не
являться элементами поля То, т. е. могут быть ненаблюдаемыми
событиями. Поле си-множеств будем называть борелевским полем
или a -полем, если оно содержит все счетные (конечные или бесконечные) объединения и пересечения своих множеств; при этом
множества из ст-поля называются борелевскими. Оказывается,
для любого поля То наблюдаемых событий всегда существует
минимальное ст-поле, содержащее То- Это минимальное ст-поле
будем обозначать Т \ оно, в отличие от То, может содержать
и ненаблюдаемые события.
Один из основных результатов состоит в том, что существует
единственное продолжение функции Ро{А}, определенной для
всех А € То, до функции Р{А}, определенной для всех множеств А из минимального ст-поля Т , содержащего То'- если
А € То, то Р{А} = Pq{A}\ функция Р{А} обладает всеми свойствами функции Ро{А}, т. е., в частности, 0 < Р{А} < 1 для
любого А € Т и если А = А\ + А 2 + - - -, где все Л; € Т и Л (Л/ = 0
при i ф /, то Р{А} — Р{А\} + Р {А 2 } + . . . . Функцию Р{А} называют вероятностной мерой, определенной на Т , или просто
вероятностью.
Отметим, что рассмотрение поля Т вместо поля То и продолжение вероятностной меры с То на Т есть некоторая математическая идеализация, потому, например, что вероятность становится
определенной и для ненаблюдаемых событий. Оказывается, этот
шаг оправдан тем, что с помощью такой идеализации многие результаты для наблюдаемых событий можно получить с затратой
значительно меньших усилий.
Пространство П точек со, ст-поле Т множеств из О и вероятностная мера Р{А}, определенная для множеств А из Т , обра-
зуют вероятностное пространство, которое будет обозначаться
(П, Т , Р). Множества из Т называются измеримыми.
2.
Пусть X = Х(ш) — конечная действительная функция, определенная для всех и> из вероятностного пространства. Говорят,
что функция X измерима, и называют ее случайной величиной,
если для любого действительного х множество всех точек ш,
для которых Х(а>) < х, принадлежит сг-полю Т . Две случайные
величины X и Y называются эквивалентными, если множество
(входящее в Т ) точек ш, таких, что Х(ш) = Y(u), имеет вероятностную меру 1.
Если X = Х(ш) — случайная величина, то вероятность F{x) =
= Р { Х < х} представляет собой неубывающую функцию вещественного переменного х, непрерывную слева и стремящуюся к О
при х —> —оо и к 1 при х —►+оо. Функция F(х) называется функцией распределения (ф. р.) случайной величины X. Если при этом
существует функция f(x), такая, что
F(x) =
/(/) dt,
то f{x) называется плотностью распределения случайной величины X. Для системы случайных величин Xi, . . . , Х п функция
совместного распределения этих случайных величин определяется как
F{x\, . . . , х п) = Р {Х 1 <
Х\,
. . . , Х п < х п},
а плотность совместного распределения этих случайных величин (если она существует) — как функция f{x\, . .. , х п), такая, что
•^1
%п
F( xi , . . . , x „ ) = | . . . | f( tu . . . , t n)dti . . . , d t n.
—оо
— ОО
Введем теперь понятие случайного процесса. Пусть состояние
какой-либо системы определяется некоторой количественной характеристикой, значение которой X{t) в каждый фиксированный
момент t не является однозначно определенным, как в случае детерминированных систем, а зависит от случайных факторов, которые влияли на систему до момента t. Будем рассматривать X(t)
в каждый фиксированный момент как случайную величину, определенную на некотором вероятностном пространстве (О, Т , Р).
При изменении t в рассматриваемом промежутке времени получа-
ется семейство случайных величин X(t), зависящих от параметра t. Заметим, что в общем случае t — это необязательно время:
t может быть любым параметром (например, пространственной
координатой), изменяющимся на произвольном множестве Т.
Математическое определение случайного процесса формулируется следующим образом. Пусть {£l,T,P) — некоторое вероятностное пространство и Т — множество значений параметра.
Случайным процессом называется конечная вещественная функция X(t ,u), которая при каждом фиксированном t e Т является
измеримой функцией от и € П, т. е. случайной величиной. Для
обозначения случайного процесса, как правило, используется
краткая форма записи: X(t) или Xt вместо X{t,u).
Пусть X(t) — случайный процесс. При каждом фиксированном
t = t\ случайная величина X{t\) —X{t\,ui) имеет определенную функцию распределения, которую обозначим F(x\,
= Р{Х (^) < х\}.
Пусть ti, .. . , t n — произвольное конечное множество значений t.
Соответствующие случайные величины X{t{), ... ,X (tn) имеют
функцию совместного распределения
F(xuti-,X 2 , t 2-, . . . ; x n, t n) =P {X (t i) < х\, . . . , X ( t n) < х п}.
Семейство всех таких совместных рапределений для п = 1, 2,. ..
и всех возможных значений tj называется семейством конечномерных распределений процесса X(t). Как выяснится из дальнейшего, многие свойства случайного процесса определяются свойствами его конечномерных распределений.
Два случайных процесса X(t) и Y(t) называются эквивалентными, если при каждом фиксированном t из множества значений
параметра t X(t) и Y(t) являются эквивалентными случайными
величинами, т. е. при каждом фиксированном t P{X(t) = Y(t)} = 1.
Семейства конечномерных распределений у эквивалентных процессов совпадают.
Из определения случайного процесса следует, что X(t,w) для
каждого фиксированного элементарного события и становится
функцией от t для всех t Е Т. Иначе говоря, каждому uj или каждому возможному исходу случайного эксперимента соответствует некоторая однозначно определенная функция от t. Эта функция x(t), определяемая фиксированным ои, описывает эволюцию
меняющейся системы в случае, когда элементарное событие и;
явилось результатом рассматриваемого случайного эксперимента.
Каждая такая функция x(t) называется реализацией, или траекторией, или выборочной функцией процесса X(t).
Иногда для обозначения как случайного процесса, так и его
реализации будет использоваться один и тот же символ. Например, it может обозначать как случайный процесс, так и его
реализацию.
Задачи
1.
Доказать, что конечномерные распределения эквивалентных случайных процессов совпадают.
Р е ш е н и е . Пусть it и гу — два эквивалентных случайных процесса, т. е. P{it = nt} — 1 при любом фиксированном t.
Обозначим
Fz(xh ti;x 2 , h ) = P{i tx <
< x2}>
Fv(xi,ti-,X2 , t 2) = Р { щ < Х \ , Щ < X 2}.
Докажем, что функции F^(x\,t\\X 2 , t 2 ) и Ff)(x\,t\\X 2 , t 2 ) тождественно совпадают.
Имеем
F ^ ( x i, h ; x 2 , t 2 ) =
p { i h ^Xl) =
I
<
х 2J
6, < * Л (
1 + р f ( & < x i \ (& 1 ± V ] ^ +
&2 < Х2 / \ 6 2 = Щ / I
I \&2 < Х2 / \ 6 2 = Щ /
, р Г(
< ХЛ (
I \&2 <~*2/
= 1 I р Г ( &i
V&2 7^ Щ / j
\ \&2
< ХЛ ( &i ^
*2/ \£<2 ф Щ
ибо события во вторых круглых скобках внутри каждого слагаемого составляют полную группу событий. При этом, поскольку
P{it Ф rjt} = 0 для любого фиксированного t, последние три слагаемых равны нулю. Далее,
р Г/ 6 ,
I V6 2
так что
< ХЛ f 6 , = щ \ 1= р Г / пн < * Л / 6 , = п н \ 1
<
V62 = %/
V% <
х 2/ \ 6 8 = %/
-^2/
JI
J’
Легко убедиться в справедливости следующих очевидных
утверждений.
Л емма 1. Д л я любых событий А и В, таких, что Р{А} =
= Р{В} = 1, будет также Р{А + В } = Р{АВ} = 1.
Лемма 2. Если для события В имеет место Р{В} = 1, то
для любого события А будет Р{АВ} = Р{А}.
Из лемм 1, 2 следует, что
Р
Г / Vh < * Л / 6 , = Щ \ 1 = р Г Vh < xi 1
1
\ Щ < Х2 / \ & 2 = щ
)1
1 % < *2 )
—PfjiXX>h >х 2 >^2)»
что и означает совпадение двумерных функций распределения
процессов & и щ. Равенство n-мерных функций распределения
при п = 3 , 4 , . . . доказывается аналогично.
2.
Пусть случайный процесс X(t) задан семейством конечномерных распределений
F(xu ti;x 2 ,t 2 ', ■■■\xn, t n)
V« = l,2, . . .
W i,*2. • • • Л -
Найти вероятность
p * = P { ( ai < X { h ) < a 2 )r\[{bx < X ( t 2) < b 2 )U(b[ < X { t 2 ) < b ' 2 )}r\
а через F\\\{u, v, z) обозначим функцию совместного распределения случайных величин U, V,Z. По условию задачи эта функция
известна. Пусть для определенности Ь\ < &2 < Ь\ < Ь'2, с\ < с%
Тогда искомая вероятность
р*=Р
{[(
а\ < U < а-2
Ь\ < V < Ь%
=Р
{ (
а\ < U < а
Ь\ < V < Ь
Поскольку все события
несовместны), то
вкруглых скобках не пересекаются (т. е.
а х < U < аг')
а х < U < а2'
Ь\ < V < &2 >+Р< Ь\ < V < Ь% +
Z <с\
Z > С2
р* = Р
'а\< U < а 2
' а\ < U < а.2 '
b [ < V < ь'2 + Р- b [ < V < b2'
Z <С\
Z>c2
Относительно 1-го и 3-го слагаемых заметим:
( а\ < U < а2Л
,
гг
а\ < U < а 2
-Р
Р< Ь\ < V < ь2 = Р
Ь\ < V < Ь2
Z>c2
' а\ < U < а 2
Г G i < и < а 2Л
Р< Ь[ < V < Ь'2 } = Р
\ Ь [ < У < Ь 2’ /
Z>c2
а\ < U < а2'
Ь\ < V < Ь2
Z < с2
a \ < U < a 2'
b [ < V < b'2
Z <с2
Введем в рассмотрение
F\i{u,v)
lim F\w(u,v,z)
Z—>"-1-00
функцию совместного распределения случайных величин U и V.
| ai < U < a 2
Найдем Р ■
Имеем:
Ь\ < V < Ь2
}•
[ и < а 2\ = { и < а Л
{ U < а\ \
+
\ \ 1 \ b xi <
\ V < b 2]
\ VV << bЬ x]
< V << bЬ 22]
+
j u < ai\
1 v < b 2)
{
{
ах < U < a 2)
( а х < U < а2
V < Ь Х ) + \ b i < V < b 2 }•
г £/ < a i ) ( (
\
U <а\ Л
V < Ъ2 ) ’
a \ < U < а2
U < a 2| _ | U < а х
V <bi
V < bi
у < ь х} + {
}■
Отсюда получаем
F\\{abb2) = Fu{a\,b\) + \Рц{а\,Ь2) — F\\{a\,b\)\ +
+ [Fnfa, bx) - Fu (ah bx)} + P
^
^
’
так что
Тогда, очевидно,
{
a \ < U < а 2Л
b\ < V < Ь% > = F\\\{a2 , b2 , С2 ) + Fm(ai, b\,C2 ) Z< c2
)
- F\u(a\,b 2 , C2 ) - ^ 111(^2>h , C2 ).
Теперь можно выписать ответ:
Р* = [^11(^2. 62) - F\w{a2 ,b 2 ,C2 )\ + [F\\{a\,b\) - F\\\{a\,b\,C2 )] - [F\\(a\, 62) - FnKai, 62. ^2)] - [^пСаг, b\) - F\\\{a2 , &i, £2)] +
+ F\n{a 2 , b 2 , c \) + F\ \ \{ a\ , bi ,c\ ) - F m (a i, 62, o ) — F\i\(a, 2 , b \ , c \ ) +
+
J такая же группа слагаемых, где вместо Ь\ и &2I
\
фигурируют значения Ъ\ и Ь'2
/
3.
Пусть эксперимент Е заключается во вбрасывании случайной точки в отрезок [0,1]. Элементарное событие ш можно отождествлять с числом из отрезка [0 , 1], которое также будет обозначаться ш. При этом множество элементарных событий О = {ш}
отождествляется со всем отрезком [0,1]. Будем предполагать, что
все точки равновозможны, так что и равномерно распределена
на [0,1]. Пусть на соответствующем вероятностном пространстве
{0,,Т,Р) определен случайный процесс £j(w), t G [0,1], следующим образом:
й и = 1‘
при
при t > ш.
Нужно найти: а) вид реализаций процесса £<(и;); б) одномерные распределения процесса
в) двумерные распределения процесса £/(w).
Р е ш е н и е . Реализация процесса £/ изображена на рис. 10.
Она представляет собой ступеньку единичной высоты со случайными длинами (ш и 1 —ш) горизонтальных площадок. Опираясь
на определение, найдем функцию одномерного распределения:
F(x, t) = Р{& < х } = P{ uj : &(u>) < x } =
при
при
при
x > 1:
1 для всех t,
х < 0:
0 для всех t,
х G (0,1]: Р{ш < t} — t.
и>
1
Рис. 10
Найдем теперь функцию двумерного распределения процесса
F(xu t\;x 2 , t 2) = Р{&! < х \,&2 < х 2} =
= P W '■6 i M < х и 6 2М < *2} =
"при
при
при
при
х\
х\
х\
х2
>
<
>
>
1,х 2
> 1:
0 или х 2 < 0:
1,х 2€ (0; 1]:
1,Х \ € (0; 1]:
^при х 2 € (0; 1], Х\ Е (0; 1]:
1 для всех t\, t2;
0 для всех t\, t2;
Р{и> < t2} = t 2 для всех t\,
Р{ш < h} = t\ для всех t2\
Р{и> < m in (fi, ^2)} = m in (^ , t2).
4.
Пусть rj — случайная величина с функцией распределения
F(x). Найти все конечномерные распределения случайного процесса & = Г] + t.
Р е ш е н и е . Найдем одномерную функцию распределения:
F^(x, t) =
< х} = P{q + t < х} = Р{г] < х — t} = F(x —t).
Найдем двумерную функцию распределения:
F^(xh ti;x 2 , t 2) = Р {&1 < * ь 6 2 < * 2} =
= Р{п + h < x i , T ] + t2 < х 2} = Р{ч <
Х\
- t \ , 7) < х 2
-
t2} =
= Р{г) < min(Xi - ti)\ = F f m i n ^ - /,)).
г=1,2
i=l,2
Рассуждая аналогично, получим «-мерную функцию распределения:
Ft(xh ti;x 2 , t 2; .. .-,xn, t n) = P{£tl < * ь & 2 < х 2,
= F( min
х п} =
(Xi-U)).
1 = 1,2, ...,п
5.
Пусть & — случайный процесс, определенный на вероятностном пространстве ($1, Т , Р ) . Пусть Л — некоторое множество
в пространстве реализаций этого процесса. Множество А будем
называть борелевским, если
{и: ^(о;) £ А } £ J-.
Пусть с = const. Рассмотрим множество
А = {6:
sup ^ < с},
te[0,1]
т. е. множество А состоит из реализаций £*, удовлетворяющих условию sup & < с. Доказать, что множество А не является борелевским.
Р е ш е н и е . Для доказательства воспользуемся следующим
известным результатом: для любого борелевского множества А
вероятность Р { ^ £ А } однозначно определяется семейством конечномерных распределений процесса
в частности, для процессов с одинаковым семейством конечномерных распределений,
каковыми являются, например, эквивалентные процессы, указанная вероятность одна и та же.
Пусть (П, Т , Р) — вероятностное пространство, где П = м =
= [0,1], и равномерно распределена на [0,1]. Определим случайные процессы &(w), t £ [0,1], и рфи), t £ [0,1], следующим образом:
&(Ш) ЕЕ 0,
При
t фи,
при
t = и.
Реализация процесса щ{и) изображена на рис. 11.
k Vt
t
о
Рис. 11
Процессы & и щ эквивалентны, и поэтому семейства конечномерных распределений у них совпадают. В то же время ясно, что
Следовательно, А не является борелевским множеством.
§ 10. Математическое ожидание, дисперсия
и корреляционная функция случайного процесса
Пусть X = Х(и>) — определенная на вероятностном пространстве (П, Т , Р) дискретная случайная величина, возможные значения которой даются конечным или счетным рядом чисел хь х г , . . . ■
Пусть множество Л г- £ Т образуют те и только те ш, для которых
Х(и>) = Х(. Тогда если ряд ^ х ,Р { Л /} сходится абсолютно, то
i
его сумма называется математическим ожиданием случайной
величины X и обозначается М{Х}:
M {X } = J 2 xiP{At}.
i
Если X — непрерывная случайная величина, имеющая плотность
распределения /(х), то по определению
ОО
М {Х}=
| xf{x)dx
—ОО
в предположении, что интеграл сходится абсолютно. В случае
расходимости интеграла (или ряда, если X — дискретная случайная величина) говорят, что соответствующая случайная величина
не имеет математического ожидания.
Математическое ожидание случайного процесса X(t) определяется формулой
m(t) = M{X{t)}.
В правой части этого равенства стоит математическое ожидание
случайной величины X(t), которую удобно интерпретировать как
сечение случайного процесса, отвечающее данному значению аргумента t. По смыслу этого определения функция m(t) есть некоторая неслучайная средняя функция, около которой разбросаны
конкретные реализации случайного процесса.
Дисперсия случайного процесса есть, по определению, неслучайная функция
которая при каждом t характеризует разброс возможных реализаций x(t) относительно среднего значения m(t). При каждом фиксированном t значение D(t) дает дисперсию случайной величины
X(t) — сечения случайного процесса, соответствующего значению
аргумента t.
Случайные величины Х\, . . . , Х п называются независимыми,
если
F(x и . . . , х п) = Fi ( xi ) . . . F n(xn)
или (если f(x 1, . .. , х п) существует)
f ( x h . . . , x n ) = f i ( x i ) . . . f n(xn);
здесь Fi{xi) — функция распределения, а /;(х/) — плотность
распределения случайной величины Xi, i = l , . . . , n . Для того
чтобы в какой-то мере охарактеризовать степень зависимости
между различными сечениями, т. е. между случайными величинами X(^i) и X(t 2 ), определяют неслучайную функцию двух
переменных
K(tu t2) = M{(X(t\) - m ( h ) ) ( m ) - m(t2))},
называемую корреляционной функцией случайного процесса X(t).
Если ввести в рассмотрение центрированный случайный процесс
X ( t ) = X( t ) - m( t ) ,
ТО ДЛЯ K(t\, t2) получим
m , t 2 ) = M { X ( h ) X ( t 2)}.
Заметим, что K(t, t) = D(t), т. е. знание корреляционной функции
случайного процесса означает, в частности, и знание дисперсии.
Если D(t) ф 0, то наряду с K(t\ ,t 2 ) рассматривают нормированную корреляционную функцию
k(th t2) =
m , t 2)
a(h)a(t2V
где a(t\) = ^ D ( h ) , cr(t2) = y/D(t2) — так называемые среднеквадратичные отклонения. Удобство от введения k(t\,t2) состоит в том, что k(ti, t2) есть безразмерная величина. Кроме того,
можно показать, что |k(t\, t2)\ < 1 при любых значениях t\ n t 2.
Используя тот факт, что для независимых случайных величин Y h Z выполняется M { Y Z ) = M { Y } M { Z } , нетрудно показать,
что k{t\, t<i) = 0, если X{t\) и ХЦ 2 ) независимы. Обратное неверно:
из условия k{t\,t 2 ) = 0. вообще говоря, не следует независимость
сечений X(t\) и ХЦ 2 ).
Задачи
1. Пусть X(t) — случайный процесс вида
X(t) — U cos 9t + V sin Ot,
где в > 0 — постоянное число, a U и V — две независимые случайные величины с равными нулю математическими ожиданиями и одной той же дисперсией D. Найти математическое ожидание m(t) и корреляционную функцию K{t\,t 2 ) процесса.
Р е ш е н и е . При каждом значении t имеем
m(t) = cos9tM{U} + s m 9 t M { V } — 0,
так что
K{t\, ti) = M { ( U cos9t\ + V sin0£i)(£7cos0^2 + У sin # ^ )} =
= cos 9t\ cos 9 t 2M{ U 2 } + sin 9t\ sin 9 t2M { V'2} +
+ (cos 9t\ sin 0^2 + sin 9t\ cos 9 t 2 )M{UV}.
В силу независимости U и V
M { U V } = M {U } ■M { V } = 0,
следовательно,
K(t\, t2 ) = Dcos9t\ cos0^2 + Dsin9t\ sin 0^2 = Dcos9(t\ — ^)2. Усложним задачу 1, считая случайными не только величины U и V, но и частоту 9, а именно: рассмотрим случайный
процесс
X(t) = U cos &t + V sin 0^,
где U, V, 0 — независимые случайные величины, причем M {U } =
= М = {У} = 0, D = M { U 2} — M { V 2}, а случайная величина 0
характеризуется плотностью вероятности f(9). Как и выше, требуется найти математическое ожидание m(t) и корреляционную
функцию K(ty, ^2) процесса.
Р е ш е н и е . Найдем
m(t) = M { U cos©^} + M { y s in 0 ^ } .
Учитывая независимость U от ©, а также V от 0 , будем иметь
m(t) = Af{I/}Af{cos0*} + M { y } M { sin @ 0 = 0.
Чтобы упростить вычисление K{t\,t2), заметим, что согласно задаче 1 условная корреляционная функция для X( t) при данном
значении в частоты 0 будет
K(tu t2) = M {X (h )X (t2) | © = в} = D cosflfa - t2).
Для нахождения корреляционной функции K(t\, t2) следует умножить это выражение на элемент вероятности f( 6 ) йв и проинтегрировать по всем возможным значениям частоты
Таким
образом,
ОО
h) —D
f{ 6 ) cos 6 {t\ —t2) d 0 .
о
Рассмотрим конкретный случай, когда
Г 2 Л
т
=<
То
1
То
7Г л2 + в2
0
при в > 0,
*
при в < 0,
где Л — некоторое положительное число (условие нормировки
ОО
| f(O)d0 = 1 выполняется при любом положительном Л). Тогда
оо
m , t 2) = —
0
COS.2(V 2) d 0 = D e M - M h - t2 1}(2).
Л -f- и
Из полученного выражения для корреляционной функции видно,
что K(t\,t 2 ) убывает по мере возрастания \t\ —
причем это
убывание тем значительнее, чем больше коэффициент А. Данное
обстоятельство можно объяснить так. График функции /(0) имеет
W Предлагаемое упрощение для вычисления K(t\, ^)» конечно, нуждается в обосновании. Опуская здесь доказательство, отметим лишь, что
оно следует из свойств 2) и 3) математического ожидания и из формулы
полной вероятности.
(2) э тот интеГрал можно вычислить методами ТФКП с помощью теоремы о вычетах (см., например: Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. — М.:
Наука, 1982).
пик 2/ ( 7гА) при в = 0. С ростом А этот пик становится все меньше
и график как бы «выравнивается». Это означает, что диапазон
практически возможных частот становится все шире, а сам процесс X ( t) — все «случайнее» (предсказать его поведение становится все труднее). Вследствие этого зависимость между сечениями
с ростом А должна уменьшаться.
3.
Пусть А — постоянное положительное число, a t\, t2 , . . . —
случайная последовательность точек на оси t, такая, что:
1) вероятность Рп(Т) того, что в интервал времени длительностью Т попадет ровно п точек, п = 0 , 1 , 2 , . . . , равна
РЛЛ = ^
ехр{ -А 7 }
и не зависит от положения этого интервала на временной оси;
2) чйсла точек, попавших в непересекающиеся интервалы времени, являются независимыми случайными величинами.
В этом случае говорят, что последовательность точек t\, t 2 , ■■■
образует пуассоновский поток с постоянной плотностью А. Рассмотрим случайный процесс X(t), все реализации которого представляют ступенчатые функции следующего вида:
го
XI
*2
при
—ОО < t < t\,
при
t \ < t < t2,
при
t 2 < t < *3.
h < t < t4,
хз
при
где значения X1.X2.X3, . . . являются реализацией последовательности независимых случайных величин Х \ , Х 2 , Х з , . .. с математическими ожиданиями, равными нулю, и одинаковой дисперсией D. Требуется найти корреляционную функцию процесса X(t).
Р е ш е н и е . Ясно, что m(t) = 0, так как М{ Х\ } = М { Х 2 } =
= М { Х з} = . . . = 0. Подсчитаем корреляционную функцию K(t, t'):
K{t,t') = M{X{t)X(t')} =
= M{X(t)X(t') IA } P { A } + м д а Д О Я Д Ж Я } ,
(1)
где событие А означает, что в интервал (t, t') попадает хотя бы
одна из точек t\, /2, h ,
, а событие В — что в интервал (t, t') не
попадает ни одна из точек t\, t 2 , h , . . . . В силу независимости слу-
чайных величин Х х, Х 2, Х$, .. . имеем M {X i X j} = M {X i} M {X j} = 0
при i ф /, так что
M {X {t )X {t ') \A } = 0.
При условии В величина X(t) совпадает с величиной X (t') и, следовательно,
M{X(t)X(t') | В} = Л1{Х2(0} = D.
Поскольку вероятность Р{В} есть Рп(Т) при п — О и Т — \t — t'\,
то получаем
K(t, t') = D exp{—\ \ t —t'\}.
Как видно, в двух последних задачах получилась одна и та
же корреляционная функция. Между тем реализации случайного
процесса имеют в этих задачах совершенно различный характер:
в задаче 2 это — синусоиды, в задаче 3 — ступенчатые функции.
Таким образом, одна и та же корреляционная функция может
соответствовать случайным процессам, имеющим различный характер реализаций.
4.
Случайный процесс X(t) определяется следующим образом.
На оси времени задан пуассоновский поток событий с плотностью А. При наступлении каждого события процесс X(t) скачком
меняет свое значение, принимая независимо от предыстории процесса случайное значение V и сохраняя его до момента наступления следующего события. Случайная величина V имеет математическое ожидание ту и дисперсию Dy. Найти математическое
ожидание, дисперсию и корреляционную функцию процесса X(t).
Р е ш е н и е . Любое сечение случайного процесса X(t) есть
случайная величина V. Поэтому
М Д О )} = M { V ) = m v ,
D{X(t)} = D { V } = Dy.
Пусть t' > t, т = t' — t. Пусть событие А означает, что между
точками t u t ' появилось хотя бы одно событие пуассоновского
потока, тогда В = А означает, что не появилось ни одного события. Имеем для корреляционной функции:
K ( t , t ' ) = M{X(t)X{t') IA } P { A } + M{X{t)X{t') | B }P {B } =
= 0 • P{A} + M { i ( / ) i ( 0 } • е~Хт = D y e - W - ^ .
При произвольном соотношении моментов t и t'
K(t,t') = О у е - ^ - ('\.
5.
Случайный входной сигнал X(t) преобразуется с помощью
реле в случайный выходной сигнал Y{t) по формуле
1
при
X(t) > 0,
0
при
X(t) = 0,
при
X(t) < 0.
-1
Входной сигнал представляет собой случайный процесс X(t), который определяется следующим образом. На оси времени задан
пуассоновский поток событий с плотностью Л. При наступлении
каждого события процесс X(t) скачком меняет свое значение,
принимая независимо от предыстории процесса случайное значение V и сохраняя его до момента наступления следующего события. Случайная величина V имеет плотность распределения /(о).
Найти закон распределения сечения случайного процесса Y(t),
а также его математическое ожидание ту, дисперсию Dy и корреляционную функцию Ky(t\, t%).
Р е ш е н и е . При любом t случайная величина Y(t) с ненулевой вероятностью принимает лишь два значения: значение 1
+оо
с вероятностью р — J f{v)dv и значение —1 с вероятностью
_
Р=
0
°
| f( v) dv = 1 —р. Следовательно, математическое ожидание
— ОО
m Y = M{Y(t)} = \ - p + ( - \ ) - p = p - p ,
а дисперсия
Dy = D{Y(t)} = (1 - (р - p ) f p + (-1 - (р - р ))2р = 4pp.
Пусть событие А означает, что между моментами t\ и ^ произошло хотя бы одно событие пуассоновского потока, тогда В = А
означает, что не произошло ни одного события. Имеем для корреляционной функции:
К Y(t, t') = M { Y ( h ) Ш
\ A } P { A } + M{Y(t\) Y{t 2 ) I
Если имело место событие А, то Y(t\) и К(^) представляют собой независимые (хотя и одинаково распределенные) случайные
о
о
величины, в силу чего M{Y{t\) Е (^) | ^4} = 0. Если же произошло событие В, то Y(t\) и У (^) представляют собой одну и ту
о
о
же случайную величину, так что M {Y {t \) F (^) \В} = Dy — 4pp.
С учетом этого получаем
Ky(tu t2) = 0 • Р{А} + Dy ■Р{В} = Dy ■е~хl'1-fel = 4рре~х^ - ^ .
6.
Случайный процесс X(t) определяется следующим образом.
На оси времени задан пуассоновский поток событий с плотностью Л. При наступлении каждого события процесс X(t) попеременно скачком принимает значения 1 и —1. Найти корреляционную функцию процесса K(t\,t 2 ).
Р е ш е н и е . Очевидно, при любом t имеем M{X{t)} = (—1) х
х 1/2 + 1-1/ 2 = 0 и
о
о
Случайная величина X(t\)X{t 2 ) может принимать лишь два значения: значение —1 с вероятностью
P{X{tx)X{t 2 ) = -1 } =
Г между t\ и t2 произошло нечетное
1 число событий пуассоновского потока
{
1 - е~2Хт
2
где г = |Ti —^|> и значение 1 с вероятностью
^
т=0
Следовательно,
(2т)!
2
Рассмотрим процесс K{t), выражающий число событий, которые произошли в случайные моменты времени в интервале [0, t).
Предположим, что этот процесс удовлетворяет следующим трем
условиям.
1. Стационарность: вероятность Ptj+T(k) наступления ровно £ событий в интервале времени [t, t + т) не зависит от t:
V t, ^ G [0, + 00)
Pt't+T(k) = PT{k),
£ = 0,1,2,...,
т. е. вероятность Pt,t+T(k) при каждом £ зависит только от длины т
интервала времени [t, t + т) и не зависит от положения этого интервала на временной оси, которое характеризуется моментом t.
2. Отсутствие последействия: вероятность Pt,t+T(k) наступления £ событий в течение промежутка [t, t + т) не зависит от
того, сколько раз и как появлялись события ранее. Это предположение означает, что условная вероятность появления £ событий за промежуток времени [t, t + т) при любом предположении
о наступлении событий до момента t совпадает с безусловной
вероятностью. В частности, отсутствие последействия означает,
что для любого конечного набора непересекающихся полуинтервалов времени [^, t\ + t i ) , . . . , [tn, tn + тп) числа К\, . . . , К п событий в них — независимые в совокупности случайные величины.
3. Ординарность: вероятность появления более одного события в интервале времени длительности t есть величина более
высокого порядка малости по сравнению с t при t —> 0:
lim PW > > ' > = < ) ■
0
t
Случайный процесс K(t), удовлетворяющий перечисленным
условиям стационарности, отсутствия последействия и ординарности, называется пуассоновским, а последовательность событий, счетчиком которых выступает K(t), называется пуассоновским потоком событий.
Можно показать, что условия 1, 2, 3 влекут за собой равенство
P{K(t) = £} =
£ = 0,1,2,...,
и данное здесь определение пуассоновского потока эквивалентно
определению, данному в § 10 при формулировке задачи 3. Следовательно, K ( t ) при любом t есть дискретная случайная величина,
распределенная по закону Пуассона с параметром At. При этом А
называется интенсивностью пуассоновского процесса. Поскольку математическое ожидание M { K ( t ) } = At, то параметр А можно
интерпретировать как среднее число событий пуассоновского потока в единицу времени.
Задачи
1.
Пусть K ( t ) — пуассоновский процесс. Для произвольной последовательности моментов ty < t 2 < ■■■ < t n и произвольной последовательности целых неотрицательных чисел k y < k 2 < . . . < k n
найти вероятность
P { K ( t y ) = ky, K ( t 2) = k 2 , . . • , K ( t n) = k n} .
Р е ш е н и е . Наряду с обозначением K ( t ) будем использовать
следующее: K ( t ' , t ") — число событий в интервале [/', t"). Пусть
сначала п = 2. Используя свойства пуассоновского процесса, можем написать
P { K ( t y ) = k h K ( t 2) = k 2 } = P { K ( t \ ) = k u K ( t u t 2 ) = k 2 - k y } =
= P { K ( t y ) = k y } ■P { K ( t u t 2 ) = k 2 - k y } =
= P { K ( t y ) = * , } • P { K ( t 2 - ty) = k 2 - k y } =
_
W l) kl
\t
ky\
(A(/2 -
I
'
ty))h ~ k'
X( t 9 - h )
( k2 - k y ) \
Рассуждая аналогично, в общем случае получим
P { K ( t y ) = ky, K ( t 2) = k 2 , . . . , K ( t n) = k n} —
=
C ~XU
. (A(^2 - ty))k2~ k'
ky\
M U-U)
( k2 - k y ) \
. (A(^n-l -
(A(^3 - t2) ) k3~ k2 - M t i - U )
( h - k 2)\
t n- 2) ) k"- ' ~kn~2
•• •
-А(*,.,-Ь_в) x
( k n- y - k n- 2)\
x
(А (^ д
~
t n - i ) ) ka
kn~ l c - \ ( t n - t „ _ \ ) _
(kn - *„_,)!
Xkne ~ xtat^'(t2 - ty)k2~ kl . . . ( t n - tn- \ ) kn~ kn-'
~
ky\(k2 - k y ) \ . . . ( k n -kn-{)\
•
2.
Пусть K(t) — пуассоновский процесс с интенсивностью Л,
a K(t) — процесс, полученный из K(t) удалением каждого события
потока (независимо от других) с вероятностью р. Найти^интенсивность такого «просеянного» пуассоновского процесса K(t).
Р е ш е н и е . Введем следующую полную группу событий: Но —
ни одно из событий исходного пуассоновского потока не было
удалено к моменту t; Н\ — к моменту t было удалено ровно одно
событие; . . . ; Нт — к моменту t были удалены ровно т событий;
Тогда
P{K(t) = k} = p { j r {K(t) = k + m}{Hm}} =
m=О
оо
= Y : P { K ( t ) = k + m ,H m} =
т —О
Р{Нт I K(t) = k + т} ■P{K(t) = k + т) =
т —О
т —О
т=О
k\
m\k\
- р)‘ Y ,'
т=0
(k + m)\
т\
= ^k\« - " ( 1 _
(A(l - p ) t ) k л_ Л(1-р)Г
k\
т. е. K(t) — пуассоновский процесс с интенсивностью А(1 —р).
3.
Найти корреляционную функцию K ^ t i , h ) пуассоновского
процесса K(t) с интенсивностью А.
Р е ш е н и е . Пусть для определенности t2 > t\. Имеем
K ps(ti,t2) = м { ( В Д - xh){K(t2) - a^2)} =
= M { K( h) K( t2)} - Xt 2 ■M{K{h)} - Xti • M{K(t2)} + x 2 t{t 2 =
= M{K(ti)(K(t2) - K(ti) + K(tx))} - Xt2 ■Xti - Xti ■Xt 2 + X2 txt 2 =
= M{K(t\){K{t2) - В Д ) } + Л * { (В Д )2} - X \ t 2. (1)
По определению пуассоновского процесса случайные величины K{t\) и K(t2) — K{t\) независимы, так что
M{K(ti)(K(t2) - K ( t i ) ) } = M { K ( h ) } M { ( K ( t 2) - K ( t x))} =
= Xtt ■(Xto —Ati) — X2UU —A2/?:
кроме того,
M{{K{h))2} = D{K(h)} + ( м д а о } ) 2 = Л/1 + (A*i)2.
Подставляя это в (1), находим
^ps(^b ^2) — Afi.
Аналогично при t 2 < h получим
Kpsih, h ) — А^2.
так что при произвольном соотношении моментов t\ и t 2 можем
написать
Kpsih, h ) = Amin(^b ^)Заметим, что, используя понятие центрированного случайного
процесса, этот результат можно получить быстрее. Например, при
t2 > t\ имеем
Aps(^i, t2 ) = M { k { h ) k { t 2 ) } = M { k m h t 2) - h h ) + k m } =
= M { k ( h ) ■№ 2) - m m
+ M{k{h)}2 =
= M { k { t x)} • M { k ( t 2) - k ( h ) } + D { k ( t x)} = о - о + м х = x t h
4.
Предположим, что на некотором шоссе поток автомобилей
можно считать пуассоновским с интенсивностью А, т. е. А — среднее число машин, проезжающих мимо неподвижного наблюдателя в единицу времени (пусть в секунду). Найти вероятность
того, что пройдет более N с, пока мимо наблюдателя проедут п
автомобилей.
Р е ш е н и е . Пусть случайная величина Т\ — интервал времени, прошедший от момента начала наблюдения до момента проезда 1-го автомобиля мимо наблюдателя; Т2 — время от момента
проезда 1-го автомобиля мимо наблюдателя до момента проезда
2-го автомобиля и т. д. Тогда искомая вероятность есть
Р{Т\ + Т2 + . .. + Тп > N}.
Найдем функцию распределения F(t) случайной величины
Т = Т\ + Т2 + . . . + Тп. Имеем
F(t) = P { T i + T2 + .. . + Tn < t } =
= Р{в промежутке [0, t) произошло число событий > п} =
= 1 —Р{в промежутке [0, t) произошло число событий < п} =
П лотн ость распределения случайной величины Т есть
■ Н т=0
е
v
_
га!
(л/|" ' 'i = '. - л » <л' ) *
(т — 1)!/
(я — 1)!
1
С ледовательно, иском ая вероятность есть
Р { Т > N} = |
N
J f ~ xe - xt dt.
' N
П оследний интеграл легко вы числяется последовательны м и н тегрированием по частям:
Ч-оо
4-оо
tn- le~x t d t = Nn le XN + ^ _ i | f - * e ~ Mdt =
N
N
+oo
N n~le~XN
\
“b
(n - 1)Nn~2e~XN
>0
“I-
(n - \)(n - 2)
3e xt dt
,0
N
N n-le-\N
\
(n _ ^ N n - 2 e -X N
“1“
f a _ щ п _ 2 )N n - 3 e - \ N
“Ь
>0
.Q
+
...
(n - 1)(n - 2)... (n - (n - 2))Nn~Xn~2+v>e~XN
••• + -------------------------- ГТГл--------------------------- +
+00
(n-l)(n-2)...(n-(n-l))
|
J e~M dt =
+
A""1
J
N
N n~l . (n — l)N n~ 2
( n - l ) ( n - 2 ) N n—3
—
XN
—e
+
+
^ _ x t
, (я .-1 )(п -2 )...2 -Л Г , ( л - l) ( n - 2 ) ...1
•••+
ЛП-1
+
A”
141
/ „
1 \I ^
-XN y * N* (/ „n - 1)!
_ (n
- 1)!
v
= e
^ \ n~k k\
Xn ^
n ~
l
k= 0
так что окончательно
'J k
1 / \ \T\k
(AAQ* ^
k\
Заметим теперь, что этот результат можно было получить
и значительно быстрее. Действительно,
Р { Т > N } = Р { Т { + Т2 + .. . + Тп > N} =
— Р {в промежутке [0,ЛО произошло не более (п —1) событий} =
п—1
(АЛО* -А N
k\
k=0
,
£
5.
Пусть K(t) — пуассоновский процесс с интенсивностью А.
Определить
Р{К{3) > 2 и 7 < К{8) < 9}.
Р е ш е н и е . Первый способ. Имеем
Р { Щ ) > 2 ; 7 < К(8) < 9} =
= Я { /ф ) > 2;К(8) = 7} + Р{/Г(3) > 2; К( 8 ) = 8} =
7
=
р { Щ ) = т}Р{К{Ъ) = 7 - т } +
т=2
8
+ Y , Р Щ Ъ ) = т}Р{К{Ь) = 8 - т} =
171=2
7
=
Р{К(3) = т}(Р{К{5) = 7 - т) + Р{К(5) = 8 - т}) +
т=2
+ р {а :(3) = 8} р {/:(5) = 0} =
-
V
(Э Д -
- з л А 5 » 7-
~ Z _ . m!
m=2
=
е -8 Л
--5 А
V ( 7 - m) ! e
у
т=2
. (5 А )» -
(8 —/га)!
И ''
. <ЗА>* - З Л .-5 А _
J+
(ЗА)" (бА)7-™ Л + _ 5А _\ +
т\ ( 7 - т ) \ \
8-т/
8! *
е _8Л
6
“
38А8
8!
7
= е -8 А д 7 у -
^
171=2
Зт 5
Л + J A _ \ + е -8Л3«А«
т!(7 - т)! V
8-т/
8!
- р - 8АА7 V - 3"57- " ( 8 - т + 5А)
л 2 -J
т \(8 —т)!
р- 8А3 ^
8!
171=2
Второй способ. Пусть F(x, у) — функция распределения двумерной случайной величины (X , Y): F(x,y) — Р{ Х < х, Y < у}\
Ру(у) — функция распределения случайной величины Y : Fy{y) =
= P { Y < у}. Выразим вероятность Р{ Х > х х\у\ < Y < у 2} через
функции F(x,y) и Fy(y). Имеем
Р { Х > х х- у х < Y < у 2 } = Р { Х > х х- Y < y 2 } - P { X > x 1; Y < у х},
Р { Х > х 1; Y < y 2} = P { Y < у 2 } - Р { Х < х Y < у 2},
Р { Х > х 1; Y < у\} = P { Y < у{\ — Р{ Х < х х; Y < У\}.
Поэтому
Р{ Х > х\\ у\ < Y < у 2} = P { Y < у 2} — Р{ Х < х х; Y < у 2} - ( . P { Y < у х} ~ Р{ Х < х\\ Y < г/j}) =
= Fy(y2) - F y ( y i ) - F { x \ , y 2) +F{x\,y\).
Пусть теперь X = К(3), Y — К(8). Тогда
p ( k h k2) =
kj
р щ з) = щ, т
2
= п2},
п 2= 0 п \= 0
где по свойствам пуассоновского процесса
при п 2 > щ :
Р{К{Ъ) = пи К(8) = п2} =
при п 2 < пу
Р{К(3) = «ь /С(8) = Л2} = 0.
П\ \
(П2-П\)\
Поэтому
8
6
Р{ЛГ(3) > 2; 7 < К( 8 ) < 9 } = J 2 ^ П е_8А " Е
/2=0
- £
^ Г е“ 8А "
/2=0
£ Я { Я ( 3 ) = = п ь *(8) = л2} +
/22=0 /21=0
+ е
= «ь а д = п2} =
е
п 2= 0 /21 = 0
= Е
/2=7
^ г е_8Л - Е
Е
г ч м з ) = 01. *(8) = " 2} =
«2=7 «1=0
< W _ -8 A
•С' V '
= /2=7
Е гг!^ 8А- Е
тЕ n
«2=7 «1=0
<З Л > " |5Л>.......
” l! («2 —« 1)!
.-8 Л
6.
Пусть для некоторого потока событий промежутки времени
между последовательными событиями представляют собой независимые случайные величины, одинаково распределенные по показательному закону с параметром А. Пусть случайный процесс
K(t) — число событий, произошедших за промежуток времени
(At)n
длительностью t. Показать, что P{K(t) = п} =
Р е ш е н и е . Пусть случайная величина Х\ — промежуток времени от момента начала наблюдения до первого события,
—
промежуток времени от первого события до второго и т.д. По
условию задачи Х \ , Х 2 , . .. — независимые одинаково распределенные случайные величины с плотностью распределения \ е ~ Хх.
Искомая вероятность есть
P{K(t) = п \ = Р{Х 1 + . .. + Х п < t\ Х\ + . .. + Х п + Х п+\ > t}.
Найдем плотность распределения случайной величины Un = Х \ +
+ . .. + Х п. Для этого воспользуемся следующим известным результатом (который уже использовался при решении задачи 7
из §7; там же приводилась идея его доказательства).
Теорема (о свертке). Если случайная величина X имеет
плотность /Дх), а случайная величина Y — плотность /2(я),
и X J независимы, то случайная величина Z — X + Y имеет
плотность
+оо
Ф(г)=
J h(x)h(z-x)dx.
— ОО
Пользуясь этой теоремой, найдем плотность распределения
фщ{%) случайной величины U2 = Х \ + Х 2 :
Z
Z
ФиЛz) = Хе-** • Xe~x{-Z~x)dx = X2 e~Xzdx
о
о
— А2е_Лг | dx = A2 ze~Xz
(г > 0).
Теперь можно найти плотность распределения фи3 (г) случайной
величины U3 = U2 + Х г:
z
фиАг) =
г
.3 2
Х2хе~Хх-Xe~x(-Z~x^dx = Хге~Хг x d x = —£ - e ~ Xz (z > 0).
По индукции получаем плотность распределения фип(г) случайной величины Un = Un- \ + Х п\
f
Фип(г) =
\ п у п- 1
?_Лг
(л —1)!
,Фип(г) = 0
при
г > 0,
при
z <. 0 .
Искомая вероятность есть
P{Un < t, Un + Х п+\ > ^},
где X„+ i — случайная величина с плотностью \е~*х и независимая с Un. Чтобы найти эту вероятность, научимся находить
вероятность
Р{ Х < х, X + Y > z},
где X — случайная величина с плотностью fx(x), Y — независимая с X случайная величина с функцией распределения FY(y).
Покажем, что
Я
Р { Х < х , X + Y > z } = | fx { t ) { \ - F Y{ z - t ) ) d t .
Будем сначала считать, что X — дискретная случайная величина.
Тогда
Р{Х<х, Х + Y > z } =
=
Y , P{X = xi t X + Y > z } =
i: Xi<x
P{ X = x i , Y > z - X i } =
i: X i < x
53 P{ X = x t} P { Y > z - X i } =
i: X i < x
= 53 P { X = x i} ( \ - P { Y < z - x i}) =
i: Xi<x
=
5 3 P {X = X i } ( \ - F Y{ z - X i ) ) .
i: X j < x
Если теперь считать, что X — непрерывная случайная величина с плотностью fx{x), то последняя сумма трансформируется
в интеграл
J fx(v)(l - F Y( z - v ) ) d v ,
— ОО
что и требовалось показать. Следовательно,
t
P{U„ < t , U „ + X n+i > 0 = 1 Фип{х){\ - FXn+l(t - *)) dx,
где Fxn+l (v) — I — е Xv — функция распределения случайной величины Х п+\. В результате получаем
t
P{Un < t, Un + X n+{ > t} = | ^ 1 ^ ( 1
\ n v n— 1
\Я
- (1 - е- Л<*-*>)) dx =
^
bJL
e~xtdx = —
e~xt
(n —1)!
(n —1)!
n\
что и требовалось доказать.
7.
Предположим, что расстояния между автомобилями, движущимися в одном направлении по некоторому шоссе, распределены экспоненциально со средним значением 50 м. Какова вероятность того, что на отрезке шоссе длиной в 1 км находятся от 20
до 30 автомобилей?
Р е ш е н и е . Пусть случайная величина Х\ — расстояние от
некоторой предварительно выбранной точки шоссе до первого автомобиля, Х.2 — расстояние от первого автомобиля до второго
и т.д. Пусть случайный процесс K(s) — число автомобилей на
участке шоссе длиной s. Тогда вероятность того, что на участке
длиной s окажутся ровно п автомобилей, есть
P{K(s) = п) = Р { Х х + . .. + Х п < s, Х\ + .. . + X n + X n+l > s}.
По условию Х \ , Х 2 , . .. — независимые одинаково распределенные случайные величины, имеющие показательное распределение с параметром А, где M X t = 1/А = 50 м. Поэтому, учитывая
результаты решения задачи 6, можем утверждать, что
P{K(s) = п } = (- ^ f e - Xs.
Требуемая вероятность
p { k 1 < M s ) < л2} = Е
р { т = п}.
n —k\
При А = 1/50, s = 1000, k\ = 20, /гг = 30 получаем
8 (сложный пуассоновский процесс). Пусть K(t) — пуассоновский процесс, но каждое у-е событие обладает индивидуальным весом Vj. Пусть Vj — независимые в совокупности одинаково распределенные случайные величины с функцией распределения F(v), не зависящей от времени. Предполагается также, что Vj,
j = 1, 2 , , и процесс K(t) независимы. Сложный пуассоновский
процесс определяется равенством
m
Q(t) = E v h
т. е. является суммой случайного числа K(t) случайных величин Vj. В качестве примера сложного пуассоновского процесса
можно привести случайный процесс суммарного объема сделок,
совершенных на бирже к моменту t. В этом случае K(t) представляет собой число сделок, совершенных к моменту t, a Vj —
объем /-й сделки.
Требуется найти математическое ожидание m(t) =MQ(t) и корреляционную функцию K(t\, t 2 ) =M {(Q(^i) —m(t\))(Q(t 2 ) —/w(^))}
процесса Q(t).
Р е ш е н и е . Для решения задачи воспользуемся аппаратом
характеристических функций. Напомним, что характеристической функцией случайной величины X называется функция
Исходя из этого определения, непосредственным дифференцированием нетрудно проверить, что между характеристической функцией v?x(s) случайной величины X и ее начальными моментами
М { Х п} имеет место следующая связь:
В частности,
Найдем характеристическую функцию случайной величины Q(t) при произвольном фиксированном t. Имеем
+00
m t ) (s) = M { e isQ^ j = ] Г M { e isQ® | K(t) = k}P{K(t) = k}.
Поскольку
M { e isQ{t) | K(t) = k } = M{Vs E /=> vi} = M { e isV'eisVi.. . eisV*} =
= M { e isVl} M { e isV2} .. . M { e isVk} = (<pv (s))k,
где (fv(s) — характеристическая функция любой из случайных
величин Vj, / = 1 , 2 , . . . (ибо они одинаково распределены), то
получаем
_ e-At . e<pv(s)-\t _ e-\t(\-ipv(s))
Следовательно,
M {Q(0} =
=
5=0
получаем для математического ожидания M {Q(0} следующий
результат:
m(t) =M{Q{t)} = At - M V .
Этот результат был отчасти предсказуем: математическое ожидание суммы случайного числа одинаково распределенных независимых случайных слагаемых равно произведению математического ожидания каждого слагаемого, т. е. M V , на математическое
ожидание числа слагаемых, т. е. At.
Перейдем теперь к вычислению корреляционной функции.
Пусть для определенности t2 > t \ . Имеем
K(th t2) = M{Q(t\) Q fe)} - m(ti) m(t2) =
= M {Q (^)(Q fe) - Q ft) + Q m } - A\ t 2 ( M V ) 2 =
= M{Q(tl)}M{Q(t2) - Q(h)} + M { Q 2 (h)} - AH M M V f =
= \ t \ M V { \ t 2 - A*i)MF + M IQ 2^ ) } - \ 2 t M M V ) 2 =
= -(A tx) 2 {MV) 2 + M { Q 2 {tx)}.
Для нахождения Af{Q2(^)} воспользуемся аппаратом характеристических функций:
*«*<«}- -(% ^ )L =0= <-1)(^{е-«—<*>,})L=o=
= (—l)A#i«fe~‘x/l(1-¥’v,<e))A/i ^ d- v{s)) 2+e~xt[ V - w W - 2f -Y-^ sl \
I
\ ds J
ds2 J s=0
= (_ , )All{Af l( ^ > ) 2 + ^
}
5=0
Учитывая теперь, что
MV = - i ( ^ e ^ j
M { V 2} =
ds2
откуда
J
( d<pv(s) \
{ -а г )
= - ( M V ) 2,
d 24>v(s)\
откуда
s= о
2
V
ds
= - M { V 2},
J 5= o
и продолжая предыдущую цепочку равенств для M {Q 2 (t\)}, получим
M{G?{tx)} = - X t x{ X h ( - \ ) ( M V ) 2 - M { V 2}) =
= (А^)2(МУ)2 + А^М{У2}.
Поэтому
K{tu t2) = \ h - M { v 2}.
Аналогично, при t\ > t2 будет K(t\ ,t2) = М 2 - M { V 2}. Таким образом, при произвольном соотношении моментов ^ и t 2 можем
написать
K(t\, t2) = А • m in(/b t2 ) - M { V 2}.
В частности, для дисперсии D{Q(£)} получим
D{Q(t)} = K(t, t) = Xt ■M { V 2}.
Заметим, что, казалось бы, прогнозируемый результат — дисперсия суммы случайного числа одинаково распределенных независимых случайных слагаемых равна произведению математического ожидания числа слагаемых, т. е. Xt, на дисперсию каждого слагаемого, т.е. D V = M { V 2} — (M V )2, — оказался здесь
ошибочным.
§ 12. Виды сходимости
в вероятностном пространстве
и характеристики гладкости случайного процесса
В отличие от обычной теории функций действительного переменного, в теории случайных процессов рассматриваются не
один, а несколько видов сходимости и соответственно различные
определения, связанные с понятием предела, в частности, определения непрерывности и дифференцируемости.
Пусть Х х, Х 2, . . . — последовательность случайных величин,
определенных на одном и том же же вероятностном пространстве; X — еще одна случайная величина, определенная на этом
же пространстве. Вводятся следующие определения трех основных типов сходимости последовательности Х п к пределу X при
п —» оо.
1. Сходимость с вероятностью 1 (другие названия: сходимость почти всюду, сходимость почти наверное). Последовательность случайных величин Х п, п = 1 , 2, . . . , сходится к случайной
величине X с вероятностью 1, если
р{и>:
и ю а д - а д } = 1.
Я — >ОО
Более подробно: каждому элементарному событию ш соответствует
некоторая числовая последовательность х\ —Х х(ш), х 2 = Х 2 (ш),...
и число х = Х(ш)\ требуется, чтобы вероятностная мера множества, состоящего из тех и>, для которых lim х п = х, равнялась 1.
п—юо
Короче это требование записывают так: Р{Хп —>X} = 1, а для
обозначения самого факта сходимости с вероятностью 1 пишут
Х п — *Х, или Х п - 2 ^ X (сокращения п.в. или п.н. означают
соответственно почти всюду или почти наверное).
2. Сходимость в среднеквадратичном. Последовательность
случайных величин Х п, п = 1 , 2 , . . . , сходится к случайной величине X в среднеквадратичном, если
lim М { ( Х п - Х ) 2} = 0.
я —»оо
L
}
Такую сходимость обозначают Х п ср’кв~> X.
3.
Сходимость по вероятности. Последовательность случайных величин Х п, п = 1 , 2 , , сходится к случайной величине X
по вероятности, если для любого заданного е > О
lim 5п = 0,
где
5п = Р{\Хп - Х\ > е).
р
Этот тип сходимости записывается так: Х п —>X.
Общее свойство, присущее всем трем определениям, можно
сформулировать так: при достаточно больших п случайная величина Х п и предельная случайная величина X близки в определенном вероятностном смысле.
Покажем, что сходимость по вероятности является самым слабым видом сходимости, т. е. как сходимость в среднеквадратичном, так и сходимость с вероятностью 1 влекут за собой сходимость по вероятности. Первое из этих утверждений следует
из неравенства Чебышёва (см. §8): если при каком-либо k > О
для случайной величины Y существует M{\Y\k}, то для любого
фиксированного е > О
M{\Y\k)
£
Взяв здесь А = 2 и положив Y — Х п — X, получим
р{\у\>е}<
Р{\Хп - Х \ > е } <
М{(Хп - Х ) 2}
е.2
Следовательно, если М{{Хп —JT)2} —> 0 при п —> оо, то и
Р{\Хп — Х\ > е} —►0 при п —♦ оо, т. е. из сходимости в среднеквадратичном следует сходимость по вероятности.
Докажем теперь, что сходимость с вероятностью 1 также влечет
за собой сходимость по вероятности. Зафиксируем любое е > О
и введем в рассмотрение событие
А е = {ш: 3 N = N(u) Ч п > N \Хп(ш) - Х{ш)\ < е}.
Если имеет место сходимость последовательности случайных величин Х п, п = 1, 2, . . . , к случайной величине X с вероятностью 1,
то Р {А е} = 1. Противоположное событию А е событие А е есть
Ae = {u:VN Зп> N
>г};
для него Р {А е} = 0. Введем событие
B£jv = {ш: 3 n > N
| Х „ М - Х И | >е}.
Тогда
оо
Ае = Ве,\В£>2Аг,3 • • • =
П
k= \
причем
В е л Э В е,2 D . . . D Bejk О В е ,Ш
О . . . .
В этой ситуации, очевидно, имеет место представление
Д-,1 — Л £ + В£у\В £у2 + В£2В££ + . . . + B£ikB£ji+1 + ...
—
+
X] ^ e’k ^£,k+1•
*= 1
Поскольку любые два слагаемых в правой части этого равенства
являются событиями несовместными, то
оо
Р{ВеЛ} = Р {А £} + ^ P { B e , k B £,k+l}.
k=\
N- 1
_______
Обозначим S N = J2 P{Be,kB£,k+1}; тогда
k=\
P{BS,l} = P {A e} + Hm SN.
N -+ o o
В силу свойства вложенности событий В£ * имеем
P{B£tkB£jk+l} = Р{ВеЛ} - Р { В еЛ+х}
для любого
k = 1,2,...;
поэтому S m = ^{Агд} - P{B£fl } и
Р{В£Л} = Р { Т £} + {Р{ВеЛ} - Jim Р{В£,лг}),
N-+00
откуда следует
Jim P{B£,N} = P{A e} = 0.
N —>оо
Введем теперь в рассмотрение событие
Се,ы = {ы: |*w(w) - X(w)| > е).
Тогда C£tN с ВеМ, так что
0 < Р{С£,м} < P{Be,N}.
Переходя в последнем двойном неравенстве к пределу при Af —>оо,
получим lim Р{Се^ } — lim Р{|Адг —Х\ > е} = 0, что и требоN —>оо
валось доказать.
’
N —>оо
Итак, сходимость с вероятностью 1, как и сходимость в среднеквадратичном, влечет за собой сходимость по вероятности.
Помимо трех выше введенных типов сходимости (с вероятностью 1, в среднеквадратичном, по вероятности) рассматривается
еще один тип сходимости — сходимость по распределению.
4.
Сходимость по распределению. Этот тип сходимости определяется следующим образом: последовательность случайных
величин У„, « = 1, 2 , . . . , сходится к случайной величине Y по
распределению, если последовательность функций распределения
Fyn(x) сходится к функции распределения Fy(x) во всех точках х,
где Fy(x) непрерывна.
Докажем, что из сходимости по вероятности следует сходимость
по распределению: если для любого е > О Р { | У „ - У | > £} ^ 0
при п —> оо, то Fyn(x) —>Fy(x) при п —» оо, если только Fy(x)
непрерывна в точке х. По формуле полной вероятности
P{Yn < x } = P {( Y n < x ) ( \ ( Y < x + e)} +
+ P{(Yn < x ) f ) ( Y > x + £ ) } < P { Y < x + s } + P { \Y n - Y \ > e } .
Аналогично
P { Y < х - е} = P { ( Y < х - e ) f ] ( Y n < х)} +
+ P { ( Y < x - e ) r \ ( Y n > x)} < P { Y n < x } + P { \ Y n - Y \ > e}.
Отсюда, вводя обозначение 8 n(e) = P{\Yn — Y\ > e} и объединяя
два последних неравенства в одно двойное, получим
Fy(x - е) -
8 п(е)
< F y j x ) < Fy(x + е) + <5„(е).
(1)
Возьмем любое сколь угодно малое Д > 0. По непрерывности Fy(x)
в точке х можно указать такое е, что Fy(x + е) и Fy(x — е) будут
отличаться меньше, чем на Д /2 . Далее, существует натуральное N, такое, что для любого п > N будет 5п(е) < Д /4 . Поэтому,
В силу (1), ДЛЯ любого П\ > N И любого П2 > N
Ргч М \ < ^
и по критерию Коши существования предела последовательности
существует предел lim Fyn(х) при я —►оо. При этом из (1) следует,
что этот предел равен Fy{x), что и требовалось доказать.
Различные определения сходимости в вероятностном пространстве приводят к различному пониманию непрерывности и дифференцируемости случайного процесса. В соответствии с определениями сходимости непрерывность и дифференцируемость слу-
чайного процесса можно понимать: а) в смысле сходимости с вероятностью 1, б) в смысле среднеквадратичной сходимости, в) в
смысле сходимости по вероятности, г) в смысле сходимости по
распределению. Приведем, например, определения непрерывности
и дифференцируемости в среднеквадратичном (ср.кв.).
Если случайный процесс X(t) удовлетворяет условию
l i m A f { ( * ( /) - * ( f o ) ) 2} = 0 ,
t — HQ
то говорят, что X(t) непрерывен в ср.кв. в точке t = to- Если
это условие выполняется во всех точках некоторого промежутка (а, Ь), то процесс называется непрерывным в ср.кв. в промежутке (а, Ь).
Если случайный процесс X(t) и случайная величина Y удовлетворяют условию
то процесс X(t) называется дифференцируемым в ср.кв. в точке to, случайная величина Y — производной в ср.кв. процесса X(t)
в точке ^о; ПРИ этом Для Y используют также обозначение
Пусть K(t, и) — корреляционная функция процесса X(t). Найдем достаточное условие непрерывности в ср.кв. процесса X(t)
в терминах его корреляционной функции. Имеем
M{{X{to + h ) - № ) ) 2 } = M{X{to + h) X( t 0 + h ) } ~
- 2M{X{to + h) X( t 0)} + M{X(t o)X(t 0)}.
Пусть m(t) = M{X{t)}. Легко проверить, что при любых t' и t"
K{t', t") = M{X{t ')X{t")} - m(t')m(t");
поэтому
M{(X{to + h) —X ( ^ o ) ) 2 } = K(t0 + h, to + h) + m(to + h)m(to + h) —
- 2K(t0 + h, to) - 2m(to + h) m(to) + K(t0, t0 ) + m(t0) m(to).
Отсюда следует, что если функция m{t) непрерывна в точке to,
a K(t,u) непрерывна в точке t — и = to, то процесс X(t) непрерывен в ср.кв. в точке to. Можно показать, что это условие является также необходимым: из непрерывности в ср.кв. процесса X(t) в точке to следуют непрерывность математического ожидания m(t) в точке
и непрерывность корреляционной функции K(t, и) в точке t = и = to-
Отметим, что непрерывность в ср.кв. процесса X ( t) в (а, Ь)
не влечет за собой непрерывности с вероятностью 1. Например,
выборочные функции процесса, рассмотренного в задаче 3 из § 10,
являются ступенчатыми с вероятностью 1 и, следовательно, разрывны. Тем не менее этот процесс непрерывен в ср.кв. в любой
точке, поскольку его математическое ожидание m(t) = 0 и корреляционная функция K(t, и) = D exp{—A|f —u|} непрерывны.
Необходимое и достаточное условия дифференцируемости
в ср.кв. процесса X(t) в точке to также можно выразить в терминах математического ожидания m(t) и корреляционной функции K(t,u). Таким условием, как можно показать, является суdm(t)
dK2 (t,u)
ществование производных —— в точке tn и — г— в точке
at
atou
t — и = to. При этом, как и в случае непрерывности в ср.кв.,
существование производной в ср.кв. еще не означает, что выборочные функции процесса дифференцируемы в обычном смысле.
Наконец, сформулируем без доказательства еще один результат, которым будем пользоваться в дальнейшем. Пусть случайный
процесс X(t) имеет математическое ожидание m(t) и корреляционную функцию K(t\, t<i). Если процесс X{t) дифференцируем
в ср.кв. и его производная в ср.кв. равна X'{t), то формулы
_
dm(t)
mdt) = ~ d r
„
"
v
Л d2K{tu k)
к ' (‘и ‘2) =
определяют математическое ожидание m\(t) и корреляционную функцию K\{t\^ t<i) процесса X'(t). Формально этот результат можно получить, если изменить последовательность выполнения операций математического ожидания и дифференцируемости
в ср.кв.:
„,</) = М { Х ' т = м { £ х ( ( > } = 1 М{Х(1)} = Jd f - ,
K d h , t2) = M{{X'{h) - m S M X ' i h ) - т Ш ) } =
= м { ± m t ) - m(t))
I at
=
£(X(t) - m(t)) I
t=txat
}=
It—t2 J
- m m ( X ( t 2) - m(/2))} =
Если интересоваться взаимной корреляционной функцией процессов X(t) и X'{t), которая по определению есть
*01 ( М 2) = М { ( Х а {) - m{tx)){X'{t2) - /щ(*2))},
то аналогичные преобразования приводят к результату
Этот результат также справедлив и может быть доказан математически строго.
Задачи
1.
Пусть X i , Х 2 , . .. — последовательность случайных величин,
Fi(x),F 2 (x), . .. — их функции распределения. Предположим, что
lim Fn(x) = G(x)
п—>оо
в каждой точке непрерывности функции G(x). Показать, что этого
условия недостаточно для того, чтобы утверждать факт сходимости случайных величин Х \ , . .. по распределению.
Р е ш е н и е . Пусть случайная величина Х п имеет функцию
распределения
0
Fn(x) = < ^
1
при х < —п,
при
—п < X < п,
при X > п,
где « = 1 , 2 , . . . . Тогда, очевидно, для любого х
lim Fn(x) =
п —*оо
1
2
.
Тем не менее функция
не является функцией распределения, так что не выполняется
определение сходимости случайных величин Х \ , Х 2 , . . . по распределению.
2.
Пусть эксперимент состоит во вбрасывании точки на единичную окружность, причем все точки попадания равновероятны
(т. е. равномерно распределены на окружности). Зафиксируем на
окружности какую-либо точку О и будем отсчитывать от нее длину дуги. Пусть ш — элементарный исход, соответствующий попаданию в конкретную точку
окружности. Условие и е [а, 0]
будем понимать как попадание точки Сш на дугу АВ, где длина
дуги ОА равна а, а длина дуги ОВ равна 0. Пусть гп — некоторая
заданная числовая последовательность, /г = 1 , 2 , . . . . Определим
последовательность случайных величин Х п — Х п(ш) следующим
образом:
2,
если
ше
1,
если
ш
Х п{ш) =
Требуется исследовать сходимость последовательности случайных величин Х п. Рассмотреть два случая задания последовательности гп:
k=\
k=\
Р е ш е н и е . В качестве предельной случайной величины рассмотрим X = 1. Исследуем сходимость по вероятности. Зафиксируем любое е > 0. Тогда
Р{\Хп- Х \ > е} = p | w € rn,r n+ ^ j | =
— С0 при л —> оо,
так что сходимость по вероятности есть. Исследуем сходимость
в среднеквадратичном:
М{(Л'„ - Х ) ! ) = \! Р\ \ Хп - Х \
1} =
= /> { * € [r„,r„ + i ] } = ± . 1 — . 0
при
00,
так что сходимость в среднеквадратичном тоже имеет место.
Покажем теперь, что в случае 1) сходимости с вероятностью 1
нет. Для этого зафиксируем любое ш = и\[х и покажем, что числовая последовательность
Х \ = Xi ( c Oi [ x ) y Х 2 — ^ 2 ( ^ f i x ) >
•••
не будет сходиться к 1. Действительно, в силу расходимости гароо 1
монического ряда ^ - при любом сколь угодно большом N найk=i
дется п* > N, такое, что и)\[х е
гп*>гп* + i ]
и
= 2.
В случае 2) при Си .х ф С, где длина дуги ОС равна сумме
0°
ряда ^ —2, для всех достаточно больших я будет выполняться
fe=i k
Г
условие Wfix ^ f n, Гп + ~ и, как следствие, х п = 1. А поскольку
^
Р{Со, = С} = О, то
Р{ш: lim ^„(ш) = 1} = 1,
П-+СЮ
что и означает факт сходимости с вероятностью 1 последовательности случайных величин Х \ , Х 2 , . . . .
Т З и Пусть случайная величина Х п, п = 1 , 2, . . . , имеет плотность распределения
fn(x) = - •
7Г
(распределение Коши).
1 + ГГХГ
Требуется исследовать последовательность Х \ , Х 2 , . . . на сходимость в среднеквадратичном и по вероятности.
Р е ш е н и е . Поскольку при п —►оо плотность распределения fn(x) становится похожей на дельта-функцию, то в качестве
предельной случайной величины естественно рассмотреть X = 0.
Исследуем на сходимость по вероятности. Зафиксируем любое
е > 0. Тогда
Р{\Хп - х \ > е } = Р{\Хп\ > е} = 1 - Р{\Хп\ < е} =
£
£
П£
1
Гг / \ j
1 2 n f dx
, 2п f 1
dt
= 1 — f J x ) dx = 1 ------------^ =1
=■• —
J
f . 1+ П Х
7Г J l + fi n
—£
о
0
2
= 1
arctg t i e — > 0 при n —►oo,
7Г
т. e. сходимость по вероятности есть.
Исследуем на сходимость в среднеквадратичном. Имеем
La J
M{{Xn - X ) 2 } = M { X l } =
| x 2f n(x)dx =
2
TLX
-4
ах.
7Г(1 + П 2Х 2)
Поскольку последний интеграл расходится при любом п, то сходимости в среднеквадратичном нет.
( 4^Привести пример последовательности случайных величин,
которая сходится по распределению, но расходится по вероятности.
Р е ш е н и е . Пусть Х п, п = 1, 2 , . . . , есть последовательность
независимых случайных величин, равномерно распределенных на
отрезке [0,1]; X — элемент этой же последовательности. Очевидно, что сходимость по распределению есть. Исследуем на сходимость по вероятности. Пусть, для определенности, е = 0,01.
Имеем
Р{\Хп - Х \ > е } > р { х я е \ 0 ; -1 - £- } , Х е [ l + £ ; l ] } =
-(ИМИ)
1 1 ^ £2
4 - 2£ + Т ’
т. е. эта вероятность не стремится к 0 при п —*■оо, так что сходимости по вероятности нет.
5.
Доказать, что пуассоновский процесс дифференцируем по
вероятности в каждой точке и его производная (по вероятности)
равна нулю.
Р е ш е н и е . Пусть K(t) — пуассоновский процесс с интенсивностью А. Зафиксируем любое сколь угодно малое е > 0. Имеем
Г K(t + h ) - K ( t )
*
0- > « } = » - я { 5 2 М
= 1- я
j®
, е } -
< е j = 1 - P{K(h) < h ■s}.
Поскольку при достаточно малых h число he будет меньше 1, то
последнее выражение равно
1 - P{K(h) = 0} = 1 - ^ХН)° ~ Н = 1 - е~хн,
откуда в силу того, что 1 —e~Xh —> 0 при h —►0, следует, что
производная пуассоновского процесса по вероятности в каждой
точке существует и ее значение равно 0.
Пусть случайный процесс X{t) устроен следующим образом:
6.
любой набор его сечений есть совокупность независимых одинаково распределенных случайных величин с известной плотностью
распределения f(x). Будет ли случайный процесс X(i): а) непрерывным в среднеквадратичном; б) непрерывным по вероятности?
Р е ш е н и е . Сначала исследуем
на непрерывность в среднеквадратичном. Для этого воспользуемся необходимым и доста-
точным условием непрерывности в среднеквадратичном. Имеем
для корреляционной функции Kx(tь ^2) процесса X(t)
а д м 2) = м {в д в д } = ( ° т ,и
|Д { л (0 } .
если
если
'
t \ = t 2 = t.
Таким образом, если
ОО
D{X{t)} ее
J (х -
mx (t)) 2 f( x ) dx > О,
где
mx (t) = M{X{t)},
— ОО
то процесс X{t) не является непрерывным в ср. кв. в точке t,
поскольку функция Kx (t\,t 2 ) разрывна в точке t\ = t 2 = t.
Исследуем теперь X(t) на непрерывность по вероятности. По
определению, непрерывность по вероятности означает, что для
любого S > О
]im P { |* (f + e) - J t ( 0 | > 5} = 0.
£—>0
Зафиксируем t и найдем P{\X(t + е) - X(t)\ > 5 } для е ф 0. По
условию случайные величины X{t + e) и X(t) независимы. Разность X(t + е) —X(t) можно рассматривать как сумму независимых случайных величин X(t + е) и —X(t). Покажем, что плотность распределения случайной величины —X(t) есть / ( —х). Действительно, пусть Y = —X; Fy{x) и fy{x) — функция и плотность
распределения случайной величины Y ; F{x) и f(x) — функция
и плотность распределения случайной величины X. Тогда
FY{x) = P { Y < x } = Р { ~ Х < х } = Р{ Х > - х } =
= \ - Р { Х < - х } = \ - F(-x),
Ш
=
Tx F y (x ) =
T x { l ~ F { ~ X )) =
/(_ Х )’
что и требовалось показать. Следовательно, по теореме о свертке
(см. решение задачи 6 из §11) плотность распределения случайной величины X(t + е) —X(t) есть
ОО
g(x)=
J f(u)f(u-x)du.
— ОО
Поэтому для любого £ ф 0
Следовательно, условие
V5 > 0
lim P{\X(t + е) - X(t)\ > 6 } = О
£—>0
не выполняется, так что непрерывности по вероятности нет.
7.
Пусть случайный процесс X(t) определен на Т = [0,1] следующим образом:
X(t) = l v "
[ V2 ,
если
если
‘ <п
t > г,
где г — случайная величина, равномерно распределенная на [0,1],
V\ и V2 — нормально распределенные случайные величины с одинаковыми математическими ожиданиями m и равными дисперсиями D > 0. Случайные величины г, V\, V2 независимы в совокупности. Доказать, что X(t) непрерывен в ср. кв., хотя все его
реализации разрывны с вероятностью 1.
Р е ш е н и е . Найдем математическое ожидание mx (t) = М{Х{ t)}.
С этой целью введем два события, образующие полную группу:
Н\ = {t < г}
Тогда Р{Н\} = 1 — t, Р{#2} =
ческого ожидания найдем
и
t.
#2 = {t > г}.
По формуле полного математи-
mx (t) = M{X(t) I Hx} P { H x} + M { X { t ) I H 2 }P{ H 2} =
= Af{Vi}(l - t ) + M { V 2}t = m - ( l - t ) + m - t = m,
т. e.
— непрерывная функция.
Найдем теперь корреляционную функцию Kx(t i,t 2 )- Пусть
сначала для определенности t\ < t2 - Введем следующие три события, образующие полную группу:
mx(t)
Н\ = { г < t\},
Н2 = {h < г < t2},
Hz = {t 2 < г}.
По формуле полного математического ожидания найдем
Kxi h, t2) = M{ X{ t x) h t 2 )} = M { h h ) h t 2) 1 Hi} ■p{H\ } +
+ M { h h ) X ( t 2) I H2} ■P{H2} + M{X( t i ) X( t 2) I Hz} ■P{Hz} =
= M { v 2 ■v 2} ■h + m { v x ■v 2} • (t 2 - h) + M { V X. Vi} ■(i - 12) =
= D ■t\ + 0 • (t 2 — ^i) + D ■(1 —^2) = D • (1 —(/2 —^i))Аналогично, при t\ > t 2 получим
X x ( h . h) — D ■(1 —(^i —tz)),
так что при произвольном соотношении моментов t\ и t<i будем
иметь
Kx {tu h ) = D - { \ - \ h - t 2\).
Поскольку
lim
4—
Kx (th t2) = Kx (t,t) = D ,
то можно утверждать непрерывность в ср. кв. процесса X(t ) (формулировку соответствующего критерия см. в теоретической части
настоящего параграфа).
Что касается разрывности с вероятностью 1 реализаций процесса X(t), то она очевидна. Действительно, непрерывность реализации означает, что случайные величины V\ и V<i совпали. Но
вероятность этого равна нулю:
P {V 1 = V2 } = P { V 1 - V 2 = 0} = 0,
ибо вероятность того, что непрерывная случайная величина V\ — V2
принимает заранее заданное значение (в данном случае нулевое),
равна нулю.
§ 13. Стационарные и нормальные процессы —
два важнейших класса случайных процессов
Во многих приложениях приходится изучать функции, определяемые случайными факторами и ведущие себя более или менее одинаково на протяжении периода наблюдения. Рассматривая эти функции x(t) как реализации случайного процесса X(t),
естественно поставить вопрос об определении некоторого свойства процесса, которое бы как-то характеризовало эту стационарность, т. е. одинаковость поведения во времени. Такое свойство
определяется как свойство инвариантности всех конечномерных
распределений процесса относительно сдвигов времени t: для любой конечной последовательности точек t\, . . . , t n совместное пмерное распределение случайных величин
X(ti + т ) , . . . , Х Ц п + т)
не зависит от т. Процесс, обладающий этим свойством, называется стационарным.
Пусть /(* 1, . .. , х п\ t\, . . . , tn) — плотность совместного распределения случайных величин X{t\), .. . , X ( t n), a f { x \ , . . . , x n\
t\ + т, . . . , t n + т) — плотность совместного распределения случайных величин
+ т), .. . , X ( t n + т) (предполагаем, что плотности существуют). Тогда для стационарного процесса X(t) при
любом т
f(x 1, . . . , x n] t h . . . , t n) = f ( x i, . . . , х п\ h +т, . . . , t n + r).
В частности, при п = 1
fixi'Ji) = f ( x i; 0),
т. е. случайная величина X(t\) при любом t\ подчиняется одному
и тому же закону распределения. Следовательно,
m(t) = M{X{t)} = М Д О )} = const
— математическое ожидание случайного процесса (если, конечно,
оно существует) не зависит от t и является постоянной величиной. Далее, при п = 2
f { x \ , X 2 \ h , t 2 ) = f ( x i , x 2; 0 , t 2 ~ h ) >
т. е. закон распределения системы случайных величин X(t\),X{t 2 )
зависит только от разности моментов времени t 2 ~ t \ . Следовательно, все остальные характеристики системы X(t\),X(t 2 ), в том
числе корреляционная функция K{t\,t 2 ), не зависят отдельно
от ti и t 2 , а полностью определяются (если, конечно, существуют)
разностью t 2 ~ t \ . K { t \ , t 2 ) = В Д , где т = ^ — hСтационарный случайный процесс называют также строго
стационарным, или стационарным в узком смысле. В приложениях часто вводится понятие стационарности в широком смысле:
случайный процесс называется стационарным в широком смысле, если его математическое ожидание постоянно, а корреляционная функция зависит только от разности аргументов. Так, например, все процессы, рассмотренные в задачах к § 10, являются
стационарными в широком смысле. Как было показано выше, из
стационарности в узком смысле следует (при условии конечности
первого и второго моментов распределений) стационарность в широком смысле. Обратное, вообще говоря, неверно.
Заметим, что функция К(т) является четной. Действительно,
если K ( t i , t 2 ) = K ( t i - г2) = К (т), то K ( t 2 , t \ ) = K ( t 2 - Ь) = К(-т).
А так как, очевидно, K ( t \ , ^2 ) = K f o , t i ) , то К(т) = К ( —т). Таким
образом, для стационарного процесса можно писать K ( t \ , / 2 ) = К(т),
где T = \ t 2 - h\ .
Применительно к стационарному процессу указанные в § 12
условия непрерывности и дифференцируемости в ср.кв. упрощаются: для непрерывности в ср.кв. необходимо и достаточно непрерывности функции К(т) при т = 0, а для дифференцируемости
в ср.кв. — существования второй производной К"{0). Так, например, процесс, рассмотренный в задаче 1 из § 10 и имеющий
корреляционную функцию К(т) = D cos 9т, непрерывен и дифференцируем в ср.кв., а процессы в задачах 2 и 3 из § 10 с корреляционной функцией К(т) = D exp{—А|т|} непрерывны в ср.кв., но
не дифференцируемы в ср.кв.
Стационарные случайные процессы встречаются на практике
довольно часто. Такими процессами можно моделировать, например: случайные шумы в радиоприборах; колебания напряжения
в осветительной сети; качку корабля, совершающего равномерное движение по прямой; колебания высоты самолета в крейсерском горизонтальном полете. Как правило, стационарным случайным процессом описывается изменение фазовых координат любой
стохастической системы, функционирующей в установившемся
режиме.
Другой важнейший класс случайных процессов образуют
нормальные, или гауссовские случайные процессы. Случайный
процесс X(t) называется нормальным (гауссовским), если при
любом п и любых
из области изменения аргумента t плотность совместного распределения случайных величин
Xi = X(ti), i = 1,2, . . . , п, является нормальной (гауссовской), т. е.
определяется формулой^
f ( x h x 2,
=
1
r::n f
(27t)”//2<ti<T2 . . . crnD1/2
1 f
\
2Z)
n (xj-m dixj-m j) }
11
<7,<т/
/'
где mi = M{Xi] — математическое ожидание случайной величины Xi, a f — M{(Xi — mi)2} = M{(Xi)2} — дисперсия случайной
величины Xi\ D — определитель л-го порядка, составленный из
коэффициентов корреляции
рц
= ~^—M{(Xi
cricrj
—
mi){Xj
—
mj)} =
(JiGj
D=
1
Pl2
Pin
P2\
1
P2n
(Pij — Pji> Pii — 0»
Pnl
Pn2
Dij — алгебраическое дополнение элемента рц определителя D.
Если ввести в рассмотрение корреляционную матрицу
(°ХХ\
Д = М {Х (Х )Т},
где
х =
W
то выражение для плотности f{ x \, x 2,
можно записать
в более запоминающемся виде:
1
f { x i, x 2, . . . , х п) =
=е х р |- 1 ( Х ) т/ Г 1х | ,
(2тг)п/ 2 у/\К\
где через \К\ обозначен определитель матрицы К.
^ Данная формула описывает невырожденный случай, когда D ф 0;
общее определение совместного нормального распределения системы
случайных величин, включающее и вырожденный случай D = 0, рассматривается ниже.
В частных случаях при п = 1 и при п = 2 из этой формулы
получаем одномерную и двумерную плотности вероятности нормального процесса соответственно:
И
/(*ьл:г) = W
T ? х
Г
1
/(x i - m i ) 2
<Яф1 2 ( 1 ^ 7 ) (.
^
0 (jci - mi)(x2 - т2) (x2 - m 2)2\ l
’
2Р
™ --------- + “ ^ Л
где р = pi 2 = Р21 = — М{{Хх - т\){Х 2 - т2)} — коэффициент
<71(72
корреляции.
Выше было дано определение п-мерного нормального распределения в так называемом невырожденном случае, когда определитель \К\ корреляционной матрицы К отличен от нуля: |/Г| ф 0.
Общее определение n-мерного нормального распределения, включающее и вырожденный случай, можно сформулировать следующим образом. Будем говорить, что вектор X размерности т имеет нормальное распределение, если существует невырожденный
нормальный вектор Y размерности k < т, такой, что компоненты
вектора X являются линейными комбинациями компонент вектора Y. Если \Кх\ = 0, то говорят, что вектор X вырожден в пространстве т измерений.
Рассмотрим следующий пример двумерного вырожденного
распределения. Пусть Х\ и Х 2 — нормально распределенные
случайные величины с нулевыми математическими ожиданиями
и корреляционной матрицей
так что \Кх\ = 0 и распределение системы {Х\,Х2) является вырожденным. Покажем, что если \Кх\ = 0, то можно подобрать
постоянные С\ и с2 так, что
ciXi + с2Х 2 - 0.
Это будет означать, что случайная точка с координатами {Х\,Х2)
все время ложится на прямую с уравнением с\Х\ + с2х 2 = 0,
и, следовательно, распределение системы (Х \ , Х 2) вырождено,
если его рассматривать как двумерное распределение.
Обозначим
с=
Потребуем, чтобы произведение стХ = с\Х\ + С2Х 2 равнялось нулю:
стХ = 0.
Тогда
0 = М{ст Х • (стХ )т } = стМ {Х Х т }с = сТКх с,
т. е.
откуда
(ci + 2сг)2 = 0,
или
с\ = —2 С2 ,
и в качестве с можно взять
Значит, условие С\Х\ + С2Х2 = 0 принимает вид Х2 = 2х\ и распределение случайного вектора X сосредоточено на прямой Х2 = 2 х\.
Наряду с системой координат Ох\х 2 введем в рассмотрение
систему координат Оу\у 2 , направив ось у\ вдоль прямой Х2 = 2 х\,
а ось у 2 — перпендикулярно этой прямой, как показано на рис. 12.
Положение случайной точки на плоскости можно характеризовать как системой случайных величин ( Х \, Х 2 ), так и системой
(Уь Y2 ). Ясно, что в силу выбора системы Оу\у 2 будет Y2 = 0.
Найдем характеристики случайной величины Y\.
Пусть еХ[, еХ2 — координатные орты системы Охух^, а еУ], еУ2
координатные орты системы Оу\у^. Тогда
1
2
f <
е ‘'| ~ е ' ' 7 5 + е ' ! 7 Г
2
е У2 — е Х\
\
1
V5 J +Gx 2 V5'
откуда
2_\
/_1
V5
(e-«i е*г) _2_
\V b
(e|/i е г/г)
V5
J_
V5 )
Поэтому из равенства
(е*. е х„)
( е У1 е г/2 )
следует
2
/ 1
л/5
_2_
V5
J_
Vл/5
л/5
\
/
откуда
/J _
л/5
2
2 \
л/5
1
\ л/5
л/5 /
1
V5
*i
Х2
_2_
"л/5
2\
л/5
_ 1_
л/5 У
Следовательно,
W i +
Г 1 = -л/5
л/5
Введем матрицу В =
Тогда
У!- = 5Х.
Для математического ожидания получим
м
{м
= й м {х } = ( ±
_ L ) Q = o,
а для дисперсии
D { Y l } = M{Yi } f } = M { 5 X X TfiT} = В ■Л1{ХХТ} • ВТ =
/J_\
V5
2_
-
Л Й С ;‘ ;
\7ь/
Задачи
1.
Доказать, что для нормального случайного процесса понятия стационарности в узком и в широком смыслах совпадают.
Р е ш е н и е . По определению, нормальный случайный процесс — процесс, у которого любой набор сечений дает нормальный случайный вектор. Из стационарности в узком смысле, как
было показано выше, всегда следует — при условии конечности
вторых моментов — стационарность в широком смысле. Покажем,
что для нормальных процессов справедливо и обратное.
Пусть X(t) — стационарный в широком смысле нормальный
случайный процесс. Покажем, что распределения векторов
/X(h)\
fX{h
0)\
\x (t„
+ Q)J
совпадают для любого натурального п и любых t\, . . . , t n,0. Это
совпадение и будет означать стационарность процесса X(t) в узком смысле.
Распределение гауссовского случайного вектора полностью
определяется вектором математических ожиданий компонент
и корреляционной матрицей. Так как процесс X(t) стационарен
в широком смысле, то для первого вектора имеем
M{X(fi)} = . . . = M{ X(t n)} = mx = M{X(t)} = const,
о
о
а для элемента kij = M{X(ti)X(tj)} его корреляционной матрицы
kij = Kx (tt, tj) = Kx (tj - ti),
О
о
где Kx (u,v) = M{X{u)X{v)} — корреляционная функция процесса X(t). Для второго вектора:
M{ X{h + 0 ) } = . . . = M{ X( t n + в ) } = тх ,
kn = M{X{U +
= X x (ti +
в,
в ) Щ
tj + в ) = K x ( ( t j +
+ в)}
в) — (t i
=
+ 0 ) ) = K x (t j — t{)
— получаем те же самые результаты для моментов первого и второго
порядков. Следовательно, имеет место совпадение распределений.
2.
Доказать, что производная в ср. кв. — при условии ее существования — стационарного в широком смысле случайного процесса есть стационарный в широком смысле случайный процесс.
Р е ш е н и е . У стационарного в широком смысле случайного
процесса X(t) математическое ожидание mx(t) = const и корреляционная функция Kx(h, ^2) = Kx(t 2 — А)- Найдем математическое
ожидание и корреляционную функцию производной X'(t ):
d2Kx {th h) _ d2Kx(t2 ~ t\) _
dt\dh
dt\ dt2
K x 'ih ’h) =
d2Kx(r)
dr2 T=t2- t x
откуда и следует, что X'{t) есть стационарный в широком смысле
случайный процесс.
3.
Пусть случайные величины Х\ и Х% (каждая по отдельности)
имеют нормальные распределения. Следует ли отсюда, что совместное распределение случайных величин Х \ н Х 2 будет нормальным?
Р е ш е н и е . Нет, не следует. Приведем пример. Пусть плотность совместного распределения f i x 1,хг) случайных величин Х\
и Х 2 имеет вид
. (x \+ x l)/(2 < 7 2)
Пр И
X iX 2 >
Q.
f i x i,x 2) = <
{ 0
При XjX2 < 0.
Проверим выполнение условия нормировки:
0
0
оо оо
/(х 1, х2) dx\ dx 2 -I- I I f i x 1, x2) dx\ dx 2 =
OOOO
= ^2
e - (x*+xi)/{2a2) d x { dx 2 =
0 0
JJ
0
0
— условие нормировки выполняется.
OO
n
e~x' /(2a2) d x ^
0
^г(|
Найдем плотность распределения f(x\) случайной величины Х\:
ОО
f i x 1) =
f { X i, X 2) d X
2
=
е-х\/( 2<т2). 1
7Г<7
J
е - 4 /V ^ ) d x 2
при
х\ > О
*?/(2<72) J _ [ е -х|/(2<г2) d x 2 при X! < О
7ГСГ
=
J
-х?/(2 а2) 1
7ГС72
0- х \/( 2 а 2)
КО
л/27П
Аналогично, для плотности распределения /(хг) случайной величины Х 2 получим
1 э-4 /(2 а2)
КО
Как видно, плотности /(xi) и f{x2) оказались нормальными, тогда
как совместная плотность f { x \, x 2) не является нормальной.
f(X2 ) =
4.
Расссмотрим пример из области банковской деятельности.
Пусть время поступления вкладов в банк описывается пуассоновским процессом с плотностью А, так что среднее число вкладов, поступающих в единицу времени, равно А. Пусть продолжительность срока вклада имеет функцию распределения F(x).
Значение процента по вкладам обозначим г и будем использовать
модель с непрерывным временем, так что капитал G после t единиц времени станет (по формуле непрерывных процентов) равным
Gexp{r£}. Пусть для простоты все вносимые вклады имеют один
и тот же размер g. Требуется найти математическое ожидание
Af{A(/)} суммарного капитала X(t) к моменту t, а также выяснить
поведение М {А(0} при t -+ оо.
Р е ш е н и е . Найдем суммарный капитал к моменту t, считая, что в начальный момент to = О этот капитал равнялся нулю. С этой целью рассмотрим произвольное разбиение интервала (to,t) промежуточными моментами s(-:
to = s 0 < s\ < s 2 < .. . < Sj_i < s i < . .. < s„_i < sn = t;
пусть n достаточно велико, а все A s(- = st- —s;_i достаточно малы. Средний вклад, внесенный за промежуток времени [s;_i,S;),
равен gXAs,. К моменту t этот вклад будет больше, чем gXAsi х
х exp{r(^ —s,)}, и меньше, чем gXAsiexp{r(t —s,_i)}; по непрерывности найдется такая точка £,• Е (st- _i,st-), что этот вклад будет равен gXAsi exp{r(t — £,)}. Пусть случайная величина Х{ —
тот капитал, который к моменту t остался на счете от вклада
gXAsiexp{r(t —£;)}, внесенного в интервал времени
Тогда если X(t) — суммарный капитал на счете к моменту t, то
x( t) = f 2 Xi,
i=i
M {x (t ) } = j 2 M{Xi).
i=i
Для вычисления M{Xi} при малых As,- приближенно можно считать, что весь вклад gXAst ехр{г(£ —£0} вносится в момент
так
что Xi принимает значение gXAsi ехр{г^ —£ )} с вероятностью р,и значение 0 с вероятностью 1 —pi, где рг- — вероятность того, что
продолжительность т,- вклада, внесенного в момент
составляет
не менее (t — £,•) единиц времени:
pt = p { n > * - & • } = 1 - р { п < t - t i } = 1 - F { t - i i ) .
Таким образом,
M {Xi ) .« gXAsi exp{r(* - 6)}(1 - F{t - &•))
M{X{t)} « £ g A A s ( exp{r(t - £ ) } 0 ~ F{t - £0),
;=i
причем приближенное равенство тем точнее, чем меньше все As;.
Точный результат получается в пределе при max As,- —►0, п —►оо
i
и дается определенным интегралом
t
J
M{X{t)} = Xg exp{r(£ - s)}( 1 - Fit - s))ds.
0
С целью найти НтЛ1{Х(/)} при t —» оо преобразуем э т о т интеграл, сделав замену переменной интегрирования и = t — s:
t
о
exp{r(£ —s)}(1 —F(t — s)) ds = — ехр{пг}(1 —F(u)) du —
о
t
t
exp{ra}(l —F(u)) du.
о
Следовательно,
ОО
lim jVf{X(0} = Xg [ ехр{гы}(1 —F(u)) du,
J
0
если интеграл сходится. Полученный результат реально означает следующее: если подождать некоторое характерное время Т,
то изменение функции m(t) = M{X{t)} практически прекратится
и можно будет считать, что m(t) — const. Пусть, например, продолжительность срока вклада распределена по показательному
закону:
F{u) = 1 —exp{ —/j,u }, ц > 0.
t — ►QO
Тогда
ОО
Xg
ОО
ехр{гы}(1 —F(u)) du = Xg j exp{(r —ц)и} du.
о
о
Интеграл сходится, если ц > г , или — < -, т. е. средняя про/i
Г
должительность вклада (именнотакой смысл имеет величина
1 00
1
- = | uF'{u)du) должна быть меньшезначения -. В этом случае
•
•
•
ОО
Xg | exp{(r —fi)u} du =
Ag
т
exp{(r —fi)u} du =
Ag
fl —r
(1 - exp{—(/i —r)T}).
о
Эти величины отличаются менее, чем на один процент, если
ехр{—(fj, — г) Т\ < 0,01, или Т > —-— In 100.
\х — г
5. Закон распределения двумерного нормального вектора
описывается следующей плотностью распределения вероятностей:
„
,
V3
=
Г
1 2 7 2
„
251
ехР \ ~ 2х ~ 2 у
х у ~ Х ~ 13у ~ У / '
Найти: а) математическое ожидание и корреляционную матрицу
этого вектора, б) плотность распределения вероятностей случайной величины Z = X — 2 Y.
Р е ш е н и е . Плотность двумерного нормального распределения
1
fix, у)
2 тгахаул/ 1
х ехр
I
- р-
х
L1 _ ( f< ( x - m
I
^ _ 2p ( х - т х) ( у - т у)
(у-
2(1 - р 2) \
Обозначим:
А =
1
2(1 - р 2)а2’
В =
2(1 —р2)&у'
С=
(1 - р 2) а х а у
Тогда
1 2 7 2
,о
25
- 2х ~ 2У
ХУ ~ Х ~ У ~ Т =
= - А ( х - тх)2 - В (у - ту ) 2 + С(х - тх)(у - ту) =
= —А ( х 2 — 2 тхх + т2) — В(у 2 — 2 туу + т2) +
+ С(ху - тух - тху + тхту).
Значения А , В , С , т х,т у находим методом неопределенных коэффициентов, приравнивая коэффициенты при одинаковых степенях
переменных х и у слева и справа, в результате чего получаем
систему уравнений
Л = 1 , Я = 1 , С = - 1,
2А т х — Сту = —1,
2Вту - Стх = —13,
- А т х2 - Вт 2 + Стхту = - у .
Решая эту систему, находим:
А = i,
В = -7,
С = -1 ,
тх = 1,
ту
Далее,
А
ау
1
о = 4 =
t>
сг; /
откуда
/=
ах - \/7<гу.
Решая теперь систему
1
2(1 - р
7
2’
2)*1
Р
(1 - р )ахау
=-1,
ах = \floy,
получаем:
1
/7
1
л/6’ а х ~ У е ’ р yfi'
Проверим совпадение коэффициента перед экспонентой:
1
271-0-* сТу \ / l -
_
1
^
(Р-
_
1 X/Q -
A" /i 1~ ^
[?
Уз
7rv/2
Корреляционная матрица
К = (
= / 7 /6 - 1 / 6
РСГхСГу\
\ р а х сгу
сг2 )
V 1/6 1/6
Далее
M Z = M X - 2M Y = mx - 2 m y = l - 2 - ( -2 ) = 5,
DZ = DX + £>{27} - 2 cov(Z, 27) = a x2 + 4of - 4 • axayp =
__ 7
4 _
/7
_1_ / ____ 1_ \
5
6+ 6
4'Уб'^бЛ
л/7У 2Таким образом, Z как линейная комбинация нормально распределенных случайных величин есть нормально распределенная случайная величина с математическим ожиданием M Z = 5 и дисперсией DZ — 5/2. Следовательно, ее плотность распределения
имеет вид
г ( \ _
Ш
6.
1
Г 1(2 - 5)2 1 _
^ _ у | ехр{ 2 '
5
}
1
Г (2 - 5)2 1
V 5 7 6XPl
5
Г
Пусть стационарный в широком смысле нормальный случайный процесс X{t) имеет нулевое математическое ожидание
mx(t) = M{X(t)} = Ои корреляционную функциюКх(т) = ахе~/з2'г2/ 2.
Найти совместную плотность вероятности /ят(я, t; у, t) сечения
случайного процесса X(t) и его производной в ср.кв. Y(t) = X'(t)
в один и тот же момент времени t.
Р е ш е н и е . Примем без доказательства, что производная нормального случайного процесса в случае ее существования есть
также нормальный случайный процесс. Этот результат является
частным случаем общего результата, состоящего в том, что любое линейное преобразование нормального случайного процесса
сохраняет свойство нормальности. Поэтому Y{t) — нормальный
случайный процесс с математическим ожиданием
m Y( t ) = M { Y ( t ) } = j tM{X(t)} = 0
и корреляционной функцией (см. задачу 3)
K
y
(t ) =
-
j
~ 2 K x ( t ) = а 1 ( 3 2 е ~ Р 2т2/ 2 (1 + т 2 ) .
ат
Взаимная корреляционная функция процессов X(t) и Y(t) есть
(см. § 12)
K x y i h , t2 ) = M{{X(t{) - mx(t\))(Y(t 2 ) - my(t2))} = - ^ K x ( t \ , t 2 ),
а с учетом стационарности
K
x y
(t )
= Кх '(т) = - а 2 х(32 те~р2т2/2.
Значит, ковариация случайных величин X(t) и Y(t)
cov(X(t),Y(t)) = K x Y(r)\r=o = 0.
А поскольку для нормальных случайных величин некоррелированность означает и независимость, то X(t) и Y(t) суть независимые случайные величины с нулевыми математическими ожиданиями и дисперсиями
D{X(t)} = Кх {т) |т=0 = a 2,
D{Y(t)} = K Y(r) |т=0 = а 2/?2.
Наконец, плотность совместного распределения независимых
случайных величин X(t) и Y(t) равна произведению их одномерных плотностей, т. е.
Ы х . Ы 1. 0 = Ы * . 0 .-/г ( ! / . 0 =
+ ^ ) } .
где
— соответствующие одномерные плотности: плотность распределения случайной величины X(t) и плотность распределения случайной величины Y(t).
7.
Исследовать на стационарность в широком смысле, вычислив математическое ожидание и корреляционную функцию следующего приращения пуассоновского процесса:
т
= w ± s)- ^ K
£
где е > 0 — заданная величина, K(t) — пуассоновский процесс
с интенсивностью А.
Р е ш е н и е . Для математического ожидания имеем
M{ N(t)} = 1 (M{K(t + е)} - Л С Д *)}) = 1(А • (t + е) - At) = А.
Корреляционная функция
KN(tu t2) = M { N ( h ) N ( t 2)} - Af{^(^)}Af{JV(f2)} =
= ± M { ( K ( h + £ ) - K{tx))(K(t 2 + £ ) - K(t2))} - A2.
Займемся вычислением математического ожидания в правой части последнего равенства. Будем для определенности считать, что
t2 > t \ . Тогда при t 2 —t\ > е случайные величины K{t\ + е) —K(t\)
и K(t 2 + е) —K(t2) независимы и
м и т + £ ) - щ х) ) { к ц 2 + £ ) - K(t2))} =
= M{K{tx + е) - K{tx)} •M{K{t 2 + e) - K(t2)} = Ae • Ae = A2e2.
Пусть теперь 0 < t2 —t\ < £. Тогда
м { т х + £ ) - m r n m + £) - к т ] =
= M { K ( t 1 + £) - K(t2) + K(t2) - K(ti)) x
X (K(t 2 + £ ) - K{tX+ £ ) + K(h + £ ) - K(t2))} =
= M{(K(t\ + e) - K(t 2 ))(K(t 2 + £ ) - K(h + e))} +
+ M {(K{t\+ £ ) - m
m
m
+ S) - к т } +
+ M { (K ( t2) - K{h)){K{t 2 + £ ) - m
+ £))} +
+ M {( K( t2) - m m m + e) - к т } =
= A • (tx + £ —t2) ■A • (t 2 —/j) + M{K{t\ + e) —K(t 2 y\ 2 +
+ A • (t 2 —^i) • A • (t 2 -t- £ —t\ —e) + A • (t2 —^i) • A • (fj + £ —t2).
Учитывая, что
M {K (tl + £ ) - K ( t 2 ) } 2 =
= D{K{t\ + £) - K(t2)} + ( М { Щ Х+ £) - K { t 2) } f =
= A • {t\ + £ — t*})
~\~£ —
,
предыдущую цепочку равенств можно продолжить следующим
образом:
м {№ \+ е)~ т т т + - к т } =
= A2(^i + s —^2X^2 ~ ^1) "Ь A2(^i + £ — ^ ) 2 Т- A(fi -Ь s —^2)“Ь
+ А2(^2 “ ^l)2 + А2(^2 —^lH^l + в —h) =
— A2(^i + в —^2X^2 —^1 +
~ ^2) + A(^i + е —^2)+
+ А2(/2 —h )(^2 — t\
t\
— ty) =
= £^A2(^i + £) + A(^i + £ —^2) H“ S)?(t 2 — t\) =
= <sA2(^1 + 6 — ^2+ ^2 — ^l) + A(^i +
так что корреляционная функция
£
—
/2) — £2A2 + £:A — A(^2 — ^l),
KN(th f2) = - —
• •1
Таким образом,
~ t\).
/
О
при
— 1\ > е,
Если же снять ограничение
— t\ > 0, то из соображений симметрии получаем окончательно
О
ЯлК^ь k ) = \ X
£
|h ~ *i| > е,
\t2 - h\ < е.
8.
Пусть значение X(t + А) дважды дифференцируемого в ср.кв.
стационарного в широком смысле случайного процесса X(t) с нулевым математическим ожиданием и корреляционной функцией
Кх(т) аппроксимируется выражением
X(t + A ) * X ( t ) + Д ^ Р .
at
Показать, что дисперсия ошибки такой аппроксимации
с точностью до малых более высокого порядка по сравнению с Д 4.
Р е ш е н и е . Поскольку M{e{t 4- А)} = 0, то
D{e{t + А)} = M{e(t + А )}2 =
= M{ X( t + е } 2 + M{X{t ) } 2 + А 2м { * ™ у - 2M{ X( t + Д)Х(*)} ~ 2ДЛ*{*(* + Д ) ^ р } + 2 Д м |х ( 0 dX(f) 1
dt
у
Чтобы выразить все слагаемые в правой части через корреляционную функцию Кх(т), вспомним общие результаты: если
MX(t) = 0, то Kx(h, t%) = М { Д (^ Ш ^ )} - В этом случае
M [ d X ( t ) Y ^ # K x (tuh)
d 2Kx(h - fr)
\ dt f
dtidt2
tl=t2= t~
dt' dt*
_
d K x ' ( t 2 - t\ )
dt i
= - K x " ( h ~ h)
h = t 2= t
t\=t2=t
= - K x "{ 0 ).
Далее
так что
M ^ X { t + Д ) ^ р } = К Х' ( - А ) = - K x ’(A),
поскольку К'х (т) — нечетная функция в силу четности Кх{т)\
М { х « ) * Ш } = К х ' ( 0 ) = 0,
так как Кх(т) — четная функция и дифференцируема в нуле,
ибо X{t) дифференцируем в ср. кв.
Учитывая все это, получим
0{е(* + Д)} =
= Кх (0)
+ Кх {0) + А 2 { - К х "{0)) - 2КХ(А) - 2А ( - К Х'(А)) =
= 2(Кх ( 0 ) - К х (А)) + 2АК х ' ( А ) - А 2К х "(0).
( 1)
Поскольку К х'{0) = К х'"{0) = 0 в силу четности Кх(т), то по
формуле Тейлора с точностью до малых более высокого порядка
Кх (А) » Кх (0) + %-Кх "{0) + ^ г 4 4)(°)2
откуда
Л ' 7
4!
з
а д д ) ~ л я / Ч 0 ) + ^ 4 4)(°)-
Подставляя эти разложения в (1), находим
D{e(t + А)} * 2 ( - ^ - К х "{0) -
+
+ 2а ( а к х "(0) + ^ г 4 4 )( ° ) ) - Д 2Я Л 0 ) =
= - A 2Kx " ( 0 ) - ^ K f ( 0 ) + 2 A 2Kx "(0) + ^ K f ( 0 ) - A 2Kx "(0) =
= т 4 4)(0).
что и требовалось доказать.
9. Корреляционная функция случайного процесса X(t) имеет
вид
Kx(tь t2) = Dx e~a
cos[(3(t2 - ^)],
где a > 0, (3 > 0. Найти дисперсию производной X'(t) в ср.кв.
процесса X(t).
Р е ш е н и е . В соответствии с общими результатами имеем
для корреляционной функции Kx<(t\,t2) производной X'(t):
к
a
t \
d?Kx(ti,t2)
Кх'«'-h) =
st,at,
=
(P Kx ih -tx )
at,at,
у. ,и
ч
= ~к* ('2' h)'
Dx >- Kx >{t\, t2)\tl=tl=t = ~ K x " ( 0).
В нашем случае
Кх (т) = Dxe ~ ar2 cos (Зт,
Кх'(т) = Dxe ~ aT2 (—.2ат cos /Зт —f3 sin (Зт),
Kx"( r ) = Dxe ~ ar2 {—2ат)(—2ат cos (Зт — (3 sin (Зт) +
+ Dxe ~ aT2 (—2a cos (Зт —2ат(—sin (Зт) ■(3 —(32 cos (Зт),
откуда получаем:
К х "( 0) = Dx ( - 2 a - (З2),
Dx >= (2а + /t ) D x .
10. Случайный процесс X(t) имеет известные математическое
ожидание mx(t) и корреляционную функцию Кх(т). Найти математическое ожидание и корреляционную функцию процесса
Y(t) = t2dX{t + 2) + tX(t - 1)
at
предположении, что производная (в ср.кв.) существует.
в
Р е ш е н и е . Имеем для математического ожидания:
M{Y{t)} =
+ tM{X{t - 1)} =
-= t 2 d M{ X( t + 2)} +
=г t2 ^ x ( r )
+ t m x (T)
dt
dr
T=t+2
r= f-l
Для корреляционной функции процесса 7 (0 получим:
Яу(0.0) =
=
+ ОЖО -
•
= м {ф !
{
+ f2h
dt\
. ^ (|± 2 ) +
at2
dX(h+ _2 ) ^
=
_ l) +
+ ^ 1 ( 0 - 1)} =
ф 2
. ^ + _ 2 ) . ^ 2 _ 1} +
at i
x° { h _ 1} °x { h _ 1}j =
+ 2)1(0 + 2)} + t\t2^-M {X(h + 2)1(0 - 1)} +
+ tlh-^-M{X{h - 1) 1(0 + 2)} + 00 M{X{h - 1) 1(0 - 1)} =
Ot2
= t 2 f* W m
K x {t2
+ ^ lo ^ ^ ( o
~ tl) + ^
2 жхК Л к
~ h - 3) +
- 0 + 3) + 0 0 ^ x ( 0 - 0 ) =
= - ^ / | ^ " ( t ) | t= ^_^ - t\t 2 Kx!(r)\T=h_ h_z +
+ Ф \ к х {r)\Tz=h_ h+z + tit 2 Kx(T)\T=h_ h .
11.
процесса
Определить корреляционную функцию Ку{т) случайного
г
У(() = аВД) + * - ^ г + с ^ ? - ,
где X(t) — стационарный, дважды дифференцируемый в среднеквадратичном случайный процесс с нулевым математическим ожиданием и корреляционной функцией Кх(т); а, Ь, с — постоянные.
Р е ш е н и е . Ясно, что MY(t) = 0. Обозначая для краткости
операцию дифференцирования точкой над переменной, имеем
K Y(tl , t 2 ) = M { Y ( t l)Y(t 2 )} =
= M {{ aX h + ЬХи + cXh)(aX t2 + bXh + cXh )} =
= M^cP'X^X^ + abXt{X t2 + acXtiXt 2 + baXtxXt 2 +
+ b2X hX h + bcXtiXt 2 + caXtlXt 2 + cbXtxXt 2 + cP’Xt^Xf^}.
Поскольку
M { X tlX t2 = KX (t\, t2) — K X (t 2 - t\) = K x ( t ) ,
M { x tlx t2
=
^ - M { x tlx t2}
=
± K x (t 2 - h)
=
M { x hx t2 =
= A 5(r),
M { x hx t2 =
M { x tlx t2
M { X hXt 2
K'x {t),
= ± K x (t 2 - h) = - K'x (r),
M { X tlX ti} = J ^ - K x (t 2 - t i) = - K fJc(T),
<% dt 2
d3
d3
М { В Д 2} =
dt\ dt\
<%<9/f
*
dt\ dt2
M { X tlXt2 = | | л 1{ З Д , } = щ К х Ц2 - h ) = K x ( t ),
M { x tlx t2
M { X tlX t2
93 M { X tlX t2} = 1^ - K x {t2 - h ) =
dtfdt 2
dA
/2
дцдц
dt\dt 2
d4
f2*,2J
K 'Z { T ),
то получаем
* у (М 2 )= Л * { Щ )Щ )} =
= a 2/ f z ( r ) + a W ^ ( r ) + а с Л Г ^ ( г ) + й а ( - ^ ( г »
+ 62( - ^ ( r ) ) +
+ &С(-А^(г) + саК'х(т) + cW ^'(r) + с 2 К ^ (г),
или, приводя подобные слагаемые,
Ky(h, h ) = а 2Кх (т) + (2ас - Ь2 )К'^т) + с2 К^(т).
12. Стационарный гауссовский случайный процесс X{t) имеет
следующие характеристики:
mx ( t ) = 0,
Кх (т)= De~a2r\
Построить распределение случайного вектора
(X(t)\
х (о = m
,
\ m j
где точка означает операцию дифференцирования в среднеквадратичном.
Р е ш е н и е . Случайный вектор Х (0 нормален, поскольку является пределом последовательности нормальных случайных векторов, получаемых линейным преобразованием нормальной системы случайных величин, определяемых процессом X(t). Ясно,
что M X ( t) = 0. Найдем элементы Кц корреляционной матрицы К:
К п = M{X{t)X{t)} = Kx (t, t) = Кх (0) = А
К 12 = M{X(t)X(t)} = M { X {h )X { t2)}\h=h =
± M { m ) x m \ k=h = щ ы ь - h)
h=h
—CY^T2 \ f I
h—h
= ^ ff( r ) U = ( ^ -- ae 2r2\
r ) n' 1I = o =_ - 2o« J2 a1
K 22 = M{X{t)X{t)} = M { X{ h )X {t 2) } \ h=:t2 =
a2
a2 M {X ( h ) X ( t2)}
<% dt 2
h~h
dt\ dt2
Kx(t2 ~ ^l)
tl=t2
^ " < r ) | „ 0 = - ( D ^ “V !) " |r =o = 2“ 2a
= М Д О Ш О } = M { X ( h ) X ( h ) } |,1=
h=t2
d3
dt\ d t 2
м щ ю хт
a3
;Kx(t 2 - *l)
h—h
?r2 \W\
*1=*2
= - В Д | г= 0 = - ( ^ - “ т ) U o = 0 ’
Хзз = M { 1 (0 * (0 } = М { В Д 1 ( г 2)} |,1=
h=h
a4
atfa*
h—h
a4
—5— xKx{t 2 —^i)
а*?а^2
h—h
U
Li UL2
= 4 v m U = - ( ^ ' “V ) IVI „ 0 = 12« 4 a
Таким образом, учитывая симметричность корреляционной
матрицы, имеем
/ D
0
—2a 2D\
Кх =
0
2 a 2D
0
\ —2a2D
0
12а4D .
Винеровским процессом, выходящим из точки w q , называется
случайный процесс W(t), 0 < t < оо, обладающий следующими
свойствами:
0) W(0) = w0;
1) для любых 0 < to < h < t2 < . ■■< tn случайные величины
W{h) - W(t0), W(t2) - W{tx), . . . , W{tn) - W{tn- 1) (т.e. приращения процесса для любых непересекающихся интервалов изменения аргумента t) независимы;
2) случайная величина W(t) — Щ з), 0 < 5 < t, имеет нормальное распределение с нулевым математическим ожиданием и дисперсией t — s.
Из этого определения следует, что все конечномерные распределения процесса W{t) нормальны с постоянным вектором
средних значений (все его компоненты равны w q ) и корреляционной функцией K(s, t) = min(s, t) (см. задачу 1 настоящего
параграфа).
К винеровскому процессу приводит изучение эволюции системы, когда медленные флуктуации состояния системы интерпретируются как результат огромного числа последовательных малых
изменений, вызванных случайными воздействиями. Такая ситуация может иметь место при описании многих явлений в физике,
экономике и других областях знания. Одним из примеров таких явлений служит известный физический процесс броуновского
движения, совершаемого взвешенной в жидкости частицей под
воздействием хаотических столкновений с молекулами. Другим
примером является процесс изменения цены на рынке: цена изменяется в результате совокупного эффекта многих случайных импульсов, являющихся следствием получения новой информации.
Это обстоятельство, как первым заметил французский ученый
JI. Башелье, приводит к тому, что процесс изменения цены также
можно рассматривать как винеровский.
Приведенные два примера являются наиболее известными
примерами винеровского процесса. Поэтому последний называют
еще процессом броуновского движения, а также процессом Башелье, или Винера-Башелье.
Покажем, как к винеровскому процессу приводит рассмотрение случайных блужданий, в которых длина 8 отдельных шагов мала, но шаги столь быстро следуют друг за другом, что
движение представляется практически непрерывным. Пусть в начальный момент частица занимала положение So = 0, а п-й шаг
приводит ее в положение
S n = Х\ + • • • + Х п,
где Xi, i = 1,2, .
— независимые случайные величины, каждая
из которых принимает значения +1 и —1 с вероятностями р и q
соответственно, р + q — 1. Тогда
M{Xi}=p-q,
М { 8 п} = ^ М Ш = (Р-я)п-,
i=1
D{Xi} = (1 - (p - q))2p + (-1 - { p - q))2q = Apq,
D{Sn} = j T D i X i } = Apqn.
i=i
Если длина отдельного шага равна не единице, а 8 , то смещение частицы после я-го шага будет равно случайной величине S n5, математическое ожидание и дисперсия которой равны Af{Sn<5} = 5Af{S„} = (р — q)n 6 и D{Sn£} = S2D{ Sn} = ApqnS2
соответственно.
Предположим, что из реальных наблюдений можно найти
среднее смещение с и дисперсию d за единичный интервал времени. Если г — число столкновений в единицу времени, то должно
быть
(р —q)rS = с,
ApqrS2 = d.
(1)
Рассмотрим случайные блуждания, в которых длина 8 отдельных
шагов мала, число г шагов за единицу времени велико, а р — q
мало, причем соотношение между ними таково, что имеют место
равенства (1), где с > 0 и ^ > 0 — заданные постоянные. Выясним, что произойдет в пределе, когда 8 —* 0, г —►оо и р —» 1/2,
причем так, что
(р —q)r 8 —> с,
ApqrS2 —►d.
Введем вероятность
Vk,n — P { S n — k }
того, что после п шагов частица окажется в положении S nS = kS.
Поставим задачу найти вероятность нахождения частицы в данный момент t в окрестности заданной точки х. Для этого нужно
выяснить поведение v^n в пределе при k —>оо и п —>оо таким
образом, что п / г —►t и kd —►х.
Пусть из первых п шагов т шагов было вправо, тогда (п —т)
шагов — влево. Событие S n = k означает, что т — (п — т) = k,
или т — (п + k)/2. Следовательно, v^<n можно рассматривать как
вероятность того, что в серии из п независимых испытаний с двумя возможными исходами было (n + k ) / 2 успехов. Эта вероятность дается биномиальным распределением:
vk<n = c („ +k)l2p(n+kV 2 qn- ( n+kV2.
По локальной теореме М уавра-Лапласа (см. §4) при переходе
к пределу будем иметь
vk<n ~ ~— <р(х), где х =
y/npq
v f c exp{ - f } '
ИЛИ
Vk,n ~
ехр (
а/27гnpq
I
где знак ~ между двумя величинами означает, что их отношение
стремится к единице. Далее:
(k - (р - д)п)2
8npq
так что
В пределе случайная величина S n8 изменяется непрерывно,
и Vktn можно трактовать как вероятность того, что S n 8 находится
между (k — 1)5 и {k + 1)5, так что отношение о^п/(25) локально
измеряет вероятность на единицу длины, т. е. является плотностью вероятности. Из предыдущего ясно, что отношение о* „/(25)
стремится к
При с = 0 и d = 1 эта формула дает плотность вероятности винеровского процесса, выходящего из нуля.
Винеровский процесс занимает заметное место в теории случайных процессов и ее приложениях. В частности, он нередко используется при математическом моделировании реальных стохастических процессов экономического и финансового содержания.
Остановимся на изучении его свойств.
Покажем, что винеровский процесс является непрерывным
в следующем смысле: для винеровского процесса W(t) существует эквивалентный ^ процесс Y(t), выборочные функции которого
с вероятностью 1 непрерывны. С этой целью докажем следующую
теор ем у ^.
Теорема 1. Пусть X(t) — случайный процесс на 0 < t < 1.
Предположим, что для всех t, t + h из отрезка [0,1]
P{\X(t + h ) - X ( t ) \ > g ( h ) } < q ( h ) ,
где g и q — четные функции от h, невозрастающие {и стремящиеся к нулю) при h 1 0 и такие, что
ОО
£g(2-")<oo,
ОО
]Г 2 ^ (2 -" ) <оо.
Тогда для X(t) существует эквивалентный случайный процесс Y(t), выборочные функции которого с вероятностью 1
непрерывны на 0 < t < 1.
Д о к а з а т е л ь с т в о . Каждому натуральному п поставим в соответствие последовательность моментов
О Напомним, что два процесса X(t) и Y(t) называются эквивалентными, если при любом заданном t выполняется P{X(t) = Y{t)} = 1.
См.: Крамер Г., Лидбеттер М. Стационарные случайные процессы. — М.: Мир, 1969.
и будем аппроксимировать процесс X(t) процессом X n(t), траектории которого состоят из прямолинейных отрезков (см. рис. 13):
X(t„,r+x) —X{tnr)
X n(t) —X(tn r) +
-(t - tn,r) При tnj < t < tn>r+1.
1/ 2"
Рис. 13
Тогда для реализаций xn(t), x n+\(t), x(t) процессов X n(t),
X n+\{t), X{t) соответственно при любом t e [tny, tn>r+1]
\Xn+l{t)
Xn{f)|
|-^(^!+l,2r+l) ~-^(^n+l^r+l)! =
=
2 [•^(^n+l,2r) "T x{tn+l,2r+2 )] =
= 2 IfJC^ n+l>2r+1) —JC^«+l,2/-)]‘b[-5C(W l,2r+l)—-^(Wl^r+2)] | ^
где введены обозначения
2 a ~^~2
^'
a = \x(tn+\2 r+\) — *(Wl,2r)|> b = \x{tn+\' 2r+\) — ^(W l,2r+2)|.
т. e. а и b не зависят от t, так что
max
\xn+i{t) - x n{t)\ <
ifl.+ ift.
WS?S?n,r+i
*
*
Таким образом, случайные величины ^ max
|Xn+i(£) —X n{t)\,
A = l^ (W l,2 r+ l) — ^ ( W l,2 r ) | И 5 =
— ^ (W l,2 r+ 2 )| с в я -
заны соотношением
max
\Xn+i(t)
WSrS?/z,/-+l
- X„(t)| <
^
поэтому
**{, max
\Xn+x(t) - * n(f)| > g(2_"-1)} <
l t n , r < t < t n tr+ 1
J
\A +
В свою очередь,
Р {\А + Х
- В > ё ( 2 - П~х) } <
< Р { ( 1 л > ^ ( 2 - " - 1)) ( j ( ± f i > ^ 2 — ') ) } <
< Р{А > ^ ( г - " - 1)} + Р{В > g(2~n- 1)}.
(3)
По условию теоремы
P { A > g ( 2 - n- l)} =
= P{\X(tn+h2 r+i) - X ( t n+h2r)\ > g(2~n- 1) } < <7(2-"-')
и аналогично
Р{В > g{2~n~1)} < q(2~n~l).
Поэтому, учитывая (2) и (3), получим
Pi
m ax
\Xn+i(t) - X n{t)\ >
< 2q(2~n~x).
Отсюда для всего отрезка [0,1] имеем
р { max |X n+l(t) - X n(t) | > g t f - * - 1)} <
2n —\
^ p {I
2
U (, 222?+ 1
^
\ * n , r < t < t n tr
/ )
1^
n—1
< V
p\
max
|X„+ i(f) - X n(t)\ >
Л H v — W+l
r= 0
s
< Г
+ 1q{2~n~x) .
Дальнейшее доказательство теоремы использует следующий
результат, формулируемый ниже в виде леммы.
Л емма. Пусть Y\,Y2, . . . — последовательность случайных
величин, а 8\,52, . . . и е\,е2, . . . — такие последовательности
оо
оо
положительных чисел, что ряды ^ 2 $ и Л £i сходятся. Если
при этом для всех п
1=1
1=1
P{\Yn+l- Y n\ > 5 n} < e n,
то существует такая случайная величина У, что Yn —> У с вероятностью 1.
Д о к а з а т е л ь с т в о леммы. Покажем, что
P{\Yn+i - Y a\ > 6п для бесконечно многих п} = 0.
(4)
Предположим противное, т. е. что эта вероятность есть е > 0.
оо
В силу сходимости ряда ^ £i можно указать такое т , что
/=1
оо
£т+1 + £т+2 + • • • “
X / £i ^ Е'
i=tn-\-1
Далее,
Р{\Уп+\ — Уп\ > 8 п для бесконечно многих п} <
< P{\Yn+\ — Yn\ > Sn для хотя бы одного п > т} <
оо
< £т+1 + £т+2 + • • • =
£i < £
i=m+\
— полученное противоречие и доказывает (4). Поэтому всюду,
за исключением, быть может, ш-множеств P -меры нуль, можно
найти такое конечное число N = N(u>), что
\У п + \{ и ) ~ У п ( и ) \ < 6 п
для всех п > N(uj). Во всех таких точках ш последовательность
У\(^), У2 (ы), . . . сходится(1) к некоторому конечному пределу у(и>).
На нулевом w-множестве, где этот предел не существует, положим по определению у(и>) = 0. Таким образом, у п(ш) —►у(и>) для
всех oj, за исключением, быть может, ш-множества меры нуль, т. е.
P{Yn -
Y} = Р{ы: у п{Ш) - у(ш)} = 1.
Лемма доказана.
Вернемся теперь к доказательству теоремы. Выше показано,
что
P j m a x |* я+1(/)
> g(2_/!_1) | < 2 n+lq( 2 - n~l).
ОО
ОО
Поскольку ^ 2 g ( 2 ~ n~ ) < оо,
2n+lq(2~n~l) < оо, то из леммы
п= 1
п=1
следует, что для почти всех о; (т. е. для всех, за исключением,
быть может, ш-множества меры нуль) последовательность функций x n{t,ui), п = 1,2, ..., сходится равномерно по t € [0,1]. Так
как x n(t, ш) — непрерывная функция от t при каждом п = 1, 2, . . . ,
О Этот факт следует из критерия Коши сходимости последовательноОО
сти и сходимости ряда
то предельная функция, которую обозначим через y(t,u), непрерывна на [0,1]. Функции y{t,uj) можно рассматривать как реализации некоторого случайного процесса Y(t). Непрерывность
почти всех выборочных функций y( t, u ) на [0,1] означает непрерывность процесса Y(t) на [0,1] с вероятностью 1.
Для всех ш при t = tn<r будет x n(t) = x(t) (по самому построению функций x n(t)); кроме того, при этих значениях t = tn,r{t)
будет x n+p(t) = x n(t) для любого р = 1, 2, . . . . Значит, в точках
/ = Ом- при любом р — 1, 2, . . . получим x n+p(t) — x(t), откуда,
в свою очередь, следует, что при t = tn,r Y ( t ) = X ( t ) с вероятностью 1.
Пусть теперь t ф tn>r для всех п и г. Будем последовательно дробить отрезок [0,1] пополам, каждый раз беря ту половину, куда попадает точка t. Выберем последовательность гп так,
чтобы последовательность точек tn,r„ совпадала с последовательностью левых концов такой системы вложенных отрезков. Тогда
0 < t — tn,rn < 2- ", t = lim t„:rn и по предположению теоремы
я д а * « ,г п) - * ( * ) | > * ( 2 - я) } <
< P{\X(tn,rn) - X(t)\ > g(t - tn<rn)} < q(t - tn,ra) < q(2 -n).
Отсюда, аналогично доказательству леммы, заключаем, что последовательность случайных величин X(tnjn) сходится к случайной величине X{t) с вероятностью 1. Далее, так как Y(t)
имеет непрерывные с вероятностью 1 выборочные функции, то
Y(tn,rn) —►Y(t) с вероятностью 1. Но, как установлено выше,
P{X(tntrn) = Y(tn<Tn)} = 1. Следовательно, и P{X{t) = 7 (0 } = 1.
Теорема доказана.
Пусть теперь W(t) — винеровский процесс, так что W ( t+ h ) —
—W(t) является для каждого t нормальной случайной величиной
с нулевым средним и дисперсией \h\. Тогда
£
P{\W{t
/>{| Г « +
+ h) —
- W{f)\
П О I > гв}} = 11—
- |
—£
exp
Если ввести в рассмотрение специальные функции
X
— оо
то
1-
/
V 2 ^\h \ ' / 2
= 1
*2
ехрГзд
y/2 ^\h \x' 2
dx =
dx-f-
expM i
0
\/2^|/г|1/2 ехр{
~щ М =
1
exp
V 2 ^\h \ ^ 2
1 -2
f щ}* =
1
= 1 -2
2|A|
4 / 2 4 ^ 2 6XP\
V 2 ^\h\V2
exp<
f l
i
H
dx
=
DO
= 1-2(ф
\h\ 1/2
Нетрудно убедиться, что
Vx > О 1 —Ф(х) <
<p(x)
Действительно, разность A(x) = <p(x)/x — (1 - Ф(х)) строго убывает
на (0, оо), ибоД '(х) = —<р(х)/х2 < 0. Поскольку же
lim
Д(х) = 0, то Д(х) > 0 для любого х > 0. Поэтому
Х-++ОС
P {\w (t
+
h) -
Щ()I > е} <
Ф
).
Пусть е = \h\a, где а е (0,1/2). Тогда
P{\W{t + h) - W(t)\ > \h\a} < 2|A|1/2- V ( N fl~1/2).
Положим по определению
g(h) = \h\a,
q(h) =
2
\ h \ W - a<p{\h\a- V 2).
Тогда ряд
OO
OO
/2=1
n—\
очевидно, сходится (например, по признаку Коши), а для исследования сходимости ряда
ОО
ОО
Y i 2 nq( 2 ~n) =
/2=1
2
' £ , 2 п(2 - п) 1/ 2 - ау { ( 2 - п)а- х/ 2) =
П= 1
ОО
ОО
= ■2^2 2п2па- п/2<р(2п/ 2~па) = 2 J 2 2n/ 2+naip{2n/2~na)
П=1
/2=1
удобно воспользоваться признаком Даламбера: если через Ьп обозначить п-й член ряда, то
°п+1 _ 2l/2+a .
Ьп
I
2__________ )_ _
e x p { - ^ -2(1- 2a)nJ
= 21/2+a • e x p | - i ( 2 (1_2a)" • 21-2a - 2(1_2a)") J =
= 21/ 2+a • exp j —^ • 2(1_2a)n(21_2a — 1) j —>• О при
n —> oo,
OO
так что по признаку Даламбера ряд ^ 2nq(2~n) сходится. Таким
/2=1
образом, условия теоремы 1 выполняются при указанных функциях g(h) и q(h), и потому существует эквивалентный процессу W(t) процесс Y(t), выборочные функции которого непрерывны
с вероятностью 1.
Покажем теперь, что винеровский процесс W(t) недифференцируем, а именно: докажем, что имеет место следующий результат.
Теорема 2. Если для какого-либо t
W(t + h ) - W ( t )
— ----- ^-------— —►Z(t)
при
.
_
я —►О
в каком-либо смысле сходимости (с вероятностью 1 , в смысле среднеквадратичной сходимости, по вероятности), то для
любых конечных z\ и z%
P{z\ < Z(t) < Z2 } = О,
т.е. с вероятностью 1 случайная величина Z(t) принимает
значения ±оо.
Д о к а з а т е л ь с т в о . Ранее было показано (см. § 12), что из
трех типов сходимости — с вероятностью 1, в среднеквадратичном, по вероятности — самой слабой является сходимость по
вероятности. Поэтому достаточно доказать утверждение теоремы
в смысле сходимости по вероятности.
Итак, пусть имеет место сходимость по вероятности:
W(t + h) - W(t) р
при
А -» 0.
h
Тогда имеет место сходимость
к Z по распределению: Fzk(x) —►
—>Fz(x) при h —» 0 в тех точках, где Fz(x) непрерывна. В соответствии с определением винеровского процесса случайная величина W{t + h) — W{t) имеет гауссовское распределение с нулевым
средним и дисперсией \h\. Следовательно, случайная величина
Z/, = ( W(t + h) — W(t))/h имеет гауссовское распределение с нулевым средним и дисперсией \h\/h 2 = \/\h\. Найдем
Zh =
lim Fzh(x) = lim P{Z^ < x} =
0
Л—s-o
lim
exp{^2 m } d v =
h-> 0
VW;
= lim
h^O
V\h\ exp</ —\h '\ v \ >jdv = lim
V
I
2 J
h^o
\/ 2 n
^
\/ 2ж
exp
и
T
du
0
при
x — —oo,
1/2
при
—oo < x < oo,
1
при
x — oo.
Обозначим
при x = —o o ,
{0
1/2 при —o o < x <
1
при
x
—
oo,
oo.
Тогда Fz(x) = F(x) в точках непрерывности функции Fz(x).
Любая функция распределения не может иметь более чем
счетное число скачков (см. решение задачи 9 к §5). Это означает, в частности, что функция распределения не может иметь
более чем счетное число точек разрыва. Следовательно, для функции Fz(x) обязательно реализуется один из следующих случаев,
в каждом из которых, как показано ниже, будет выполняться
утверждение теоремы 2.
1) Fz(x) не имеет точек разрыва при х € (—о о , о о ) . Тогда она
совпадает с F(x) и
P { z x < Z < z 2} = F z ( z 2) - Р2 (21) = F ( z 2) - F(zO = ^ ~ ^ = 0
при любых конечных z\ и z 2, т. e. вероятность того, что случайная величина Z попадет в какой-либо конечный интервал, равна
нулю.
2) Fz (x) имеет конечное или счетное число точек разрыва. Тогда для любых z \ , z 2 е ( —о о , о о ) найдутся z \ е ( —o o . z i )
и z \ € {z2, о о ) , такие, что Fz {x) будет непрерывна в точках z* и г\,
так что
P{zi < Z < z 2} < P { z \ < Z < z * 2} =
= Fz { z l ) ~ F z {z\)-- F { z l ) - F { z \ ) = \ - \ = 0,
т. e. P{z\ < Z < z 2} = 0 — вероятность того, что случайная величина Z попадет в какой-либо конечный интервал, равна нулю.
Теорема 2 доказана.
Задачи
1.
Показать, что винеровский процесс W(t) является нормальным, а его корреляционная функция Kw(s, t) = min(s, t).
Р е ш е н и е . Без ограничения общности можно считать, что
процесс выходит из нуля: W(0) = 0. Пусть t\ < t2 < . . . < tn —
произвольный набор временных моментов. Для доказательства
нормальности процесса W(t) нужно проверить нормальность
вектора
/т ь )\
т ь)
С этой целью заметим, что
1
1
О
1
О\ /
W(t\)
- ЩО) \
О I
W{t2) - W { t x)
1
1
1 / \г а « ) -
Все компоненты вектора
/
W{tx) - W(0 ) \
W(t2) - W{tx)
\ W ( t n) независимы и имеют нормальное распределение. Поэтому вектор
/
W (ti)-W (0) \
W(t2) - W(h)
\ W ( t n) - W(tn- i) J
является нормальным, т. е. система случайных величин — компонент вектора имеет совместное нормальное распределение. А поскольку линейное преобразование — в данном случае умножение
на матрицу — сохраняет свойство нормальности, то нормальным
будет и вектор
[ m t i)\
W (h)
\ m t n)J
откуда и следует нормальность процесса W(t).
Получим теперь формулу для K w ( s , t). Считая для определенности t > 5, имеем
K w { s , t ) = M { ( W { s ) - w Q) ( W { t ) - w 0)} =
= M {(№ (s) - \Г (0 ))(Щ 0 - ir(s ) + №(s) - Г (0 ))} =
= M { ( r ( s ) - Г ( 0 ) ) ( Г ( 0 - r ( s ) ) + (W(s) - Щ О))2} =
= М {(Щ д) - Щ 0 ))(Щ /) - TF(s))} + M { ( r ( s ) - Щ 0 ))2}.
Поскольку математическое ожидание независимых случайных величин равно произведению их математических ожиданий, то получаем отсюда, учитывая свойства процесса W{t), что K(s,t) = s
(при t > s), что и требовалось доказать.
2.
Пусть W(t) — винеровский процесс, выходящий из нуля.
Найти корреляционную функцию случайного процесса
X(t) = W { t ) - t W { \ ) , T A e
*€[0,1].
Р е ш е н и е . Поскольку M {W ( t) } = 0, то M{X(t)} = 0 и
K xduti) = М {Х (Ь )Х (Щ =
= M { { W { t x) - t xW(\)){W{t 2 ) - t 2 W{\))} =
ТР(*2)} - <iM{1P(1)1Г(*2)} - *2М{Щ1)w(h)} +
=
+ t\t<2M { W 2(\)} = min(*i, t2) - t\t 2 - t2 t\ + t\t 2 = min(*i, *2) - t\t2.
3.
Пусть W(t) — винеровский процесс, выходящий из нуля.
Показать, что процесс
ХЦ) = е * ® - ' / 2 - \
является центрированным и имеет ортогональные приращения.
(Последнее означает, что для любых t\, t2, h , U, таких, что t\ <
< t 2 < h < *4, имеет место M{{X{t2) — X (^ ))(Z (^ ) —АХ*з))} = 0.)
Р е ш е н и е . Имеем для математического ожидания
л е д * ) } - e~t/ 2M { e w(t)} - 1.
Определим M { e w^ } . Так как W(t) есть нормально распределенная случайная величина с нулевым математическим ожиданием
и дисперсией t, то
ОО
М{е™ } = -±=
| t f e - * / ™ dx
r e-(*-t)V( 2t)d x = e t/2
ч/2л7 J
—oo
Значит,
y/ 22тг
irtt J
—oo
л е д * )} =
•
е ~ {/ 2 e f/ 2
-1
= 0,
и процесс X(t) является центрированным.
Пусть *i < *2 < h < *4. Имеем
M { ( X ( t 2 ) - X m ( X ( t 4 ) - X ( t 3))} =
= M { ( e w(t2)~ t2/2 - e w(h)~h/2) { е Щ и ) ~ Ы 2 - e W(h)~hl2)} =
= м { е Щк)+ти)-(* 2+ иу2} __ щ е тн)+ти)-(к+к)/2} _
- M { e W(t2)+^«з)-«2+/з)/2} + M {e mh)+mh)-(h+h)/ 2 y
^
Найдем
м { е щ ь)+ть)} = м { # т ь ) + щ и ) - т к ) } _
= M { e 2 w^ } - M { e W M ~ w^ } ;
так как W{t2) есть нормально распределенная случайная величина с нулевым математическим ожиданием и дисперсией t2,
то 2 W{t2) есть нормально распределенная случайная величина
с нулевым математическим ожиданием и дисперсией 4t2\ поэтому
(см. выше)
M{<?w^ } = е^ 2 = е2\
поскольку W(t\) — W(t2) есть нормально распределенная случайная величина с нулевым математическим ожиданием и дисперсией t4 —t2, то (см. выше)
W(t4) -W (t2) \ = е ( и - Ш 2
в результате
M { e w(f2)+w{ti)} = e2ti ■e{t4~t2)/2.
В ы числяя аналогично все другие математические ож идания
и продолж ая цепочку равенств (5), получим
M{(X{t2) - X(ti))(X(t4) - X(t3))} = e2t2 • e (t4~ t2)/ 2 ■е ~
_ e 2h . e ( h - t i ) / 2 . e - ( h
+
+ k
)/2 _
.
e 2ti . e ( h ~ h ) / 2
e 2t2
. e (t3 - t 2) / 2 .
e - ( h + t 3) / 2 =
gh _
^ + и)/ 2
e - ( h + t 3) / 2
gh
_
eh
+
-
+
eh
= o,
что и требовалось доказать.
4.
Пусть W { t ) — винеровский процесс, выходящ ий из нуля;
т — полож ительны й параметр. Требуется исследовать на стационарность процесс
X(t) =
+
W(t
T )-W (t).
Р е ш е н и е . Из определения винеровского процесса следует,
что
M{X(t)} = M { W { t + г) - 1Г(0} = 0.
Считая для определенности
t2 > t \ ,
найдем корреляционную функцию
K x ( h , t 2 ) = M { { W { h + т) - W ( h ) )( W ( t 2 + г) - W(t2))} =
- М { W{h + т) W(t 2 + г)} - М { W i h ) W { t 2 + т)} - M { W { t x + r ) W ( t 2)} + M { W { t x) W (t2)} =
= m i n ( / i + r , t 2 + т) - m i n ( / i , t 2 + r ) - m i n ( ^ + r , t 2 ) + m i n ( ^ , t 2 ) =
_
[t \ +
т
- t\ - {t\ +
t
)
+ t\ = 0
\ t \ + T - t \ - t 2 + t \ = T - {t 2 - t \ )
при
(t2 -
при
{t 2 - t \ ) < T .
t\) > r ,
Очевидно, что при t2 < *1 следует поменять индексы местами.
Поэтому при произвольном соотношении моментов t\ и t 2 имеем
при
При
\t2 - * i | > т ,
\t2 ~ t \ \ < T .
Таким образом, случайный процесс X ( t) стационарен в широком
смысле. Будет ли он стационарным в узком смысле?
Поскольку W{t) — нормальный процесс (см. задачу 1), то для
любого натурального п и любого набора моментов t \ ,t 2, . . . , t n
вектор
fW (tx+ T )\
ть)
W(t 2 + т)
m t 2)
W(tn + r)
mtn ) J
явдяется нормальным, т. е. система случайных величин — компонент вектора имеет совместное нормальное распределение. Если
теперь заметить, что
/Х(п)\
X(t2)
\X ( t n) /
/ 1 -1
0 0
\0
0
0
1
0
0 . . . 0
-1 ... о
о 0
0
1
...
0
0 0\
-1/
mu)
W(t 2 + r)
W ( t 2)
m tn+ r)
m tn )
то можно утверждать, что вектор
( X ( t ON
X(t2)
\X(tn)J
нормален, ибо он представляет собой линейное преобразование
нормального вектора. Следовательно, X(t) — нормальный случай-
ный процесс, а для нормального процесса понятия стационарности в узком и в широком смыслах совпадают.
5.
Показать, что сумма квадратов приращений винеровского
процесса, соответствующая разбиению а = to < t\ < . . . < tn- \ <
< t n = b отрезка [а ,Ь], сходится к (b —а) в среднеквадратичном
при измельчении разбиения:
'П—1
Мr<{| X ) W ( * i+ i) - T O ) ) 2- ( f r - a ) } 2 - 0
'/=0
при
тах(*/+1—*,) -> 0.
(6)
Р е ш е н и е . Для доказательства найдем математическое ожидание и дисперсию суммы
Е ( т н ) - щ * ) > 2.
1=0
Имеем
M J 2 ( W ( t i+l)
i= 0
- w r n 2 = ] T m ( T O +i) - w r n 2 =
i= 0
= £ D{ W{ti+X) - w m
i=0
=| >
i=0
+i - U) = b — a.
(7)
Далее, в силу независимости приращений W(ti+1) — W(U) можем
написать
D J 2 (W(ti+1) - w m
/=0
2
= E D ( W ( t i+1) - T O ) ) 2 =
i= 0
= ] Г { м W m ) - T O ) ) 4 - [л д т о + i ) - T O ) ) 2]2}i= 0
Поскольку
Af(TO-+1) - щи))2 = D(w(tM ) oo
expj
M(w(ti+l) - w m A= f *4 • —
wm
= tw
- u,
£?___ |
f<)^
=3(/w - f f)2,
то получаем
D j 2 m t i+,) - w ( u ) ) 2 =
[3«i+i - и ) 2 - (ti+1 - n)2} =
i=0
/=0
= 2 £ ( f i+1 -
U)2 <
2 m a x (fj+ i -
i=о
‘
= 2(6 - a) m ax(/i+i - *,•) —»• 0
i
при
U)
- О =
i=0
max(^+i - U) —»• 0.
i
С другой стороны, по определению
D ^ m ti+ i) - п т 2=
i= 0
i=0
i=0
откуда с учетом (7) и (8) и следует требуемое равенство (6).
(8)
Пусть W(t) — винеровский процесс, X(i) — непрерывный
в ср.кв. случайный процесс, такой, что случайный вектор с компонентами X{t\), . . . , X ( t n) не зависит от Щ я) — W(t) при любом п и любых значениях t\ < . .. < tn < t < s. Пусть а и b > a —
два фиксированных момента на временной оси. Любому п и любому разбиению г
а — to < t\ < . . . <
< tn = b
поставим в соответствие случайную величину
Yn,r = J 2 X ( t d m t i+l) - W(u)).
i=о
Обозначим через 5Т мелкость разбиения г, т. е.
5Т = max (ti — ti - 1).
Если существует случайная величина У, такая, что
M ( Y - Yn%Tf ^ 0
при
п —►оо,
6Т
-> 0,
(1)
то она называется стохастическим интегралом Ито в интервале (а, Ь) от случайного процесса X(t) по процессу W(t); при этом
пишут:
ь
У = | X(t) dW(t).
а
Для обозначения факта среднеквадратичной сходимости часто
используют символ l.i.m., так что равенство (1) можно переписать
в следующем эквивалентном виде:
Y = l.i.m. Ул>т,
или, более подробно,
f xw dW(t) =
X(ti)(W(tw ) - W(ti)).
Можно показать, что необходимым и достаточным условием
существования интеграла Ито является существование определенного интеграла
ь
^M { X{ t)} 2 dt.
Опуская доказательство этого утверждения, перейдем к примерам.
Пусть W(t) — винеровский процесс, выходящий из нуля. Положим X{t) = W{t) и найдем
о
Введем разбиение т: 0 =
< h < ■■■< tn- i < tn = T. Представим
W(T) = {W{tx) - W { t ())) + {W{t 2 ) - m t x ) ) + . -- + (W( tn) - W \ t n_ x)).
Возведем в квадрат:
W 2 (T) = £ ( Щ * т ) - m u ) f +
(=0
+ 2 ( w ( t n) - m t n. x)) J 2 ( n t i +l) - w m
i=0
+
+ 2( w ( t n^ ) - w ( t n_ 2 ) ) nj2 m t i + x ) - w m +
i= о
. .. + 2(W(t2) - W ( m w { h ) - W(to)) =
i= 0
. . .
(=0
откуда
w m w ( t i+x) - w m
= \w
2 {T)
- i ^ V t e + i ) - w m 2.
/=0
1=0
Поскольку первое слагаемое в правой части от разбиения не зависит, то
Т
п -\
I W{t)dW(t) = ± W 2(T) - i U . m . ' £ ( W i t l+i) - w m 2-
Но (см. задачу 5 к § 14)
- W ( t i ) f = Т.
i=0
Следовательно,
т
W(t)dW(t) = X
^ W 2 {T) - -ХТ .
о
Рассмотренный пример показывает, что со стохастическими
интегралами Ито нельзя обращаться как с обычными интегралами; в частности, для них не имеет места обычная формула замены
переменных в определенном интеграле.
Определим интеграл от случайного процесса G(t) по t на отрезке [t0, Т1
т
| G{t) dt
to
как предел в среднеквадратичном соответствующих интегральных сумм Римана:
Z
п —1
G(t) dt =
t
l.i.m.
mf x ( ^ + i
J 2 G(rk)(tk+i - tk),
k —0
me to < t\ < .. . < tn_ 1 < t n - T , T k e [tk, tk+\\. Последнее равенство означает: существует случайная величина Z (обозначаемая
т
как | G(t)dt), такая, что
iО
lim
m \z max(^+l-^)^0 I
k=0
G(Tk)(tk+i - tk) \
)
=0
при любом выборе точек т* е [tk, tk+1]> или, более подробно: для
любого числа е > 0 существует число <5 = 5(e) > 0, такое, что для
любого разбиения to < t\ < .. . < tn_\ < tn = Т при любом выборе
точек Tk € [tkJk+1] будет выполняться неравенство
M $ Z - ^ 2 G(Tk){tk+1 - t k) \
k=o
J
< £,
если только мелкость разбиения m ax(4+i —tk) будет меньше 5.
k
Можно показать, что необходимым и достаточным условием
•
существования интеграла J G(t) dt является интегрируемость корto
реляционной функции K q {u , v) процесса G(t) по квадрату to < и ,
v < 7, т. е. существование кратного интеграла
тт
J
Kg(u,v) du dv
to to
от неслучайной функции K q {u , v ). Например, существует интеграл
т
W(t) dt
(2)
от винеровского процесса W{t) на любом отрезке [0, 7], ибо для
винеровского процесса K w ( u , v) = min(i/, v) и
тт
тт
K w ( u , v) du d v -
min(i/, v) du dv =
оо
оо
l
и
duty
т
Г/
I
v dv
2
+ J u fifo j = Ц т г +
(T — u ) u j d u
= ^ T 3.
Если интеграл j G(r) dr от случайного процесса G( t ) существо
вует при любом t € [?о> Л . т0 можно говорить о случайном процессе
t
Y(t) — | G( t ) dr, to < t < T.
to
При этом можно показать, что математические ожидания my(t),
mo(t) и корреляционные функции КуЦ\Л 2 ),К-в(ЬЛ2) процессов
Y(t),G(t) связаны соотношениями:
t
hh
m Y(t) = j т 0 (т) dr, K Y{t\, t2) = j j Ка{т\,т2) drj dr2;
to
to to
в частности, дисперсия
t t
Dy(t) =
K g { t \ , t 2)
to to
dr\ dr2.
Интеграл, как и производная (в случае их существования) от нормального случайного процесса, есть снова нормальный процесс^.
Поэтому, например, (2) является нормальной случайной величиной с нулевым математическим ожиданием и дисперсией Т3/ 3.
Пусть теперь процесс Z/ = Z{t) представим в виде
t
t
Z t = Z 0 + j G(t) dt + J X(t) dW(t),
где Wt = W(t) — винеровский процесс, a G(i) и
принадлежат тому классу случайных процессов, для которых определены
соответствующие интегралы. В этом случае для краткости говорят, что процесс Zt имеет стохастический дифференциал dZt,
и пишут
dZt = Gtdt + X t dWt.
Последнее равенство называют также стохастическим дифференциальным уравнением относительно неизвестного случайного
процесса Zt, при этом случайные процессы G/ и Xt в правой части
в общем случае могут зависеть от Zt.
Теорема. Пусть F(t,x) — неслучайная функция, непрерывно
дифференцируемая по t е [О, Т] и дважды непрерывно дифференцируемая по х € ( —о о . о о ) . Тогда случайный процесс F(t,Zt)
имеет стохастический дифференциал, причем
dF(t,Zt) = (
+ Gt
x= Zt
+
dF(t, х)
дх
dF(t, х)
дх
dt +
x= Zi
X t dWt +
x —Z t
1 d 2F(t,x)
2 дх 2
X f dt.
(3)
x= Z t
Формула (3) называется формулой Ито. Она устанавливает
правило, по которому можно заменять переменные в стохастическом интеграле. Обратим внимание, что в случае, когда G, X
и Ц 7 - неслучайные функции, формула останется прежней, с той
лишь разницей, что не будет последнего слагаемого (получится
обычная формула для дифференциала сложной функции).
Доказательство сформулированной теоремы приводить не будем. Однако покажем, как результат (3) может быть получен на
(11 Это следствие общего результата, состоящего в том, что линейное
преобразование нормального процесса сохраняет свойство нормальности.
интуитивном ур овн е^, или, как говорят, на физическом уровне
строгости. С этой целью выпишем разложение Тейлора для выражения F{t + dt, Zt + dZt) как функции двух переменных с точностью до членов порядка не более, чем dt:
F(t + d t , Z t + dZt) * F(t ,Z t) + ^ dt + ^ dZt + \ ^ i d t f +
пренебрегаем
+
± ^ №
) 2+
+
^ d t d Z t « F(t,Zt) + ^ dt+ g ( Gt d t + X t dWt) +
Z dx
(G? (dtf + 2 GtX t d td W t + X f ( d W tf ) +
\
'
пренебрегаем
d2F
+ ^ g ( G t(dt ) 2 + X t dtdWt)
пренебрегаем
» F{t,Zt) + ^ d t + ~ ( G t dt + X t dWt) + \ ^ X
2 {dWt)2,
(4)
где все частные производные функции F(t,x) берутся в точке
(t,Zt). Поскольку
т
l.i.m.
] T ( W tk - W tk_ x) 2 = Т,
\ { d W t)2 =
m a x fe —4 _ i ) —>0 ь _ х
то в (4) можно положить (dWt ) 2 = dt, и тем самым равенство (3)
доказано.
Рассмотрим пример. Пусть
F ( t , x ) = x n,
Gt = 0,
X t = l.
Тогда формула (3) дает
d ( W t)n = n W ? ~ l d W t + |л ( л - 1) W tn ~ 2 dt,
т. e.
t
w n_wn=
0
t
nW^~ d W T + \ n ( n ^ n w ; - 2 dT
0
^ Строгое доказательство можно посмотреть в каком-либо математическом курсе теории случайных процессов, напр.: Вентцель А.Д. Курс
теории случайных процессов. — М.: Наука, 1975.
Рассмотрим еще один пример. Пусть Z* — случайный процесс
изменения стоимости акций. Упоминавшийся выше JI. Башелье,
анализируя в 1912 г. данные на Парижском рынке ценных бумаг,
пришел к выводу, что M { A Z t} = 0, а при малых A t математическое ожидание M { A Z t } 2 пропорционально At, или, если коэффициент пропорциональности обозначить a 2, M { A Z t } 2 = a 2 At.
Данные условия будут удовлетворены, если принять
dZt — d dWt,
или
Zt =
Z
q
+ dWt,
где Wt — винеровский процесс.
Позже, в 1965 г., П. Самуэльсон модифицировал модель Башелье, предложив для описания Zt использовать уравнение
^ = li d t + v d W u
(5)
А
т. е. предположив, что процессу типа броуновского движения подвержено не абсолютное, а относительное изменение цены акции.
При этом первое слагаемое в (5) интерпретируется как некоторая
общая неслучайная (и потому прогнозируемая) тенденция в изменении Zt, а второе — случайная составляющая.
Найдем решение стохастического дифференциального уравнения (5). Для этого перепишем его в виде
dZt = //Zf dt + oZt d Wtn
и воспользуемся формулой Ито (3). Положив F(t,x) = 1пх, при
G(t) = jiZt и X(t) — aZt имеем
dQnZt)=fiZt ( - \
V + f - l
\ x \ x = Z t/
~2
)<rZt dW t +
\X \x = Z tJ
z ) a<2Z^ d t = l^dt+adWt—^ a 2 dt = ^ —^ a 2 ^jdt+adWt,
•.•.
t
In Zt —ln Z 0 =
откуда при постоянных р
t
( y - ' - a ^ d t + ^adW t,
о
а получим
Z(t) —Zo exp{fit} ехр|сгИ^ —
Таким образом, в принятой модели цена акции ведет себя как банковский счет Z q ехр{^/} со случайным множителем е х р —-сг2^ |.
Задачи
1.
Доказать, что винеровский процесс W{t) интегрируем в среднеквадратичном на [ОД]:
7 (0 = jV (r )rf T ,
и найти корреляционную функцию Ky(t,s) процесса 7(0Р е ш е н и е . Как было указано в основном тексте параграфа,
необходимым и достаточным условием существования интеграла
в среднеквадратичном
JW) dt
от случайного процесса G(t) является существование интеграла
ТТ
|
KG{t\,t 2 ) d t \ d t 2
оо
от корреляционной функции K G(t\,t 2 ) процесса G(0; при этом
t
Ky(t, s) =
S
JJKc(t\, t2 ) dt\ dt 2 00
В нашем случае в роли процесса G(t) выступает винеровский
процесс W(t), и Kw{t\ , ^2) = min(^i, /2)- Пусть пока s > t, тогда
t
S
Ky(t,s)=
t
min(^i, t^) dt\ dt 2 =
00
S
^ min(^i, t%) dt\^dt<i —
00
— ^ min(^i, /2) dt\ + min(/i, t<i) d t\ ^ d t 2 =
0 0
h
t
=
+ h ( t 2 - ^ ) d t 2 = ^ 2(3s - t).
0
Очевидно, что при произвольном соотношении моментов t и s,
обозначив
а = m in(^ s), b = тах(£, s),
получим
K Y(t,s) = ^ а 2(36 —а).
О
В частности, при а = b = s = t
1. 3
Ky{t, t) = Dy(t) = -t'
— дисперсия процесса Y(t).
2. Пусть
^
X(t) =
^TdW(T),
о
где W ( t ) — винеровский процесс. Найти математическое ожидание mx {t) и дисперсию Dx (t) процесса X(t).
Р е ш е н и е . По определению стохастического интеграла
X(t)=
l.i.m.
j £ t k[W(tk+l- W ( t k) l
m a x (^ +1- 4 ) - > 0 k= Q
Поэтому, используя свойство перестановочности операций вычисления математического ожидания и предельного перехода, получим
MX(t) = М
1-i.m.
iX t k [W(tk+l- W ( t k)] =
m a x ( tk+ i - t k) - ^ 0 k=Q
=
lim
J T tkM[W{tk+x - W{tk)\ = 0,
m a,x(tk+ i - t k)-+ 0 k= Q
ибо M[W(tk+\ — W(tk)] = 0 по определению винеровского процесса.
Найдем теперь дисперсию:
Dx { t ) = M { X { f ) } 2 = M [
l.i.m.
j E t k[W{tk+l- W { t k) ] x
{m
t k) ^ 0 k= Q
m ax(tk+la x ( t k+ \—tk)—>0
l.i.m.
? ! tl [W(tj + l - W ( t j ) } \ =
max(tj+l-tj)-* 0 ._ q
=
lim
J
1 -Г (4 )]Е ^ [Г (^ 1 -Щ ^ )]} =
4=0
=
/ =0
lim
m { x : t2[W{tk+1max{tk+l- tk)-^0 Kk=Q
J
w m 2},
)
где последнее равенство обусловлено следующим свойством винеровского процесса: M{ { W( t k+\) —W(tk))(W(tj+{) - W{tj))} = 0
при k Ф j. Далее,
Ит
м { ) г t\[W(tk+\ - Щ ^ ) ] 2) =
m^x(^+i tk)
£=q
=
Ит
£
t 2M [W{tk+1 - w m
2
=
m a x f e + i - / * ) - + ( ) k=()
=
lim
/г- l
j.
i
У ' i \ ^ i k — \ u 2 du = - / 3,
J
m a x ( ^ + i - ^ ) ^ 0 fe=0
так что £>*(/) = (1/3)/3.
3.
Найти взаимную корреляционную функцию Kx'y(t 1J
производной в среднеквадратичном X (t) и римановского интеграла в среднеквадратичном
t
Y(t) = Х(и) du
о
от случайного процесса X(t) в предположении, что X '(/) и Y(t)
существуют.
Р е ш е н и е . Действуя согласно определению, имеем
J
KX>Y(t l J2) =M{ X' W( t 2) } =
„Г..
X(h + г) - X(t\)
= М< l.i.m .---------------------£
£—^0
1
l.i.m. > Х( щ ) А щ > ,
ш ах А щ - ^ 0
)
где u\,U 2 , . . . , ип—\ — точки разбиения отрезка [0 ,^ ]: 0 = щ <
< и\ < U2 < ■.. < ип_ 1 < ип = t 2 , А «г = ип — ип-\. Далее пользуемся свойством перестановочности операций вычисления математического ожидания и предельного перехода:
. . Г, .
X(/i + s) —X(t\) , .
v/ \ л 1
M l l.i.m. ——----— l.i.m. > Х ( щ ) А щ > =
1 £—>0
£
maxAwj—
>0т^
J
i
1=1
=
Um
• •••,+ £ ) - • , ) • 1 ( • [ ) • • • =
£—^0, m ia x Аггj—►
()
J
1— 1
lim
д , | А Ь 1+А ) - Ы
е—>0, m a x Л и , —>0
lim
е—>0, m a x А г/ j —>0
г
я
V
г= 1
^-
^
м , йа|1
^
fo(<i + е. Щ) ~ *x(*i, щ)
£
'
=
Mxituu) ^
dt\
где /Сх(о, ы) — корреляционная функция процесса X(t).
2
4.
Напомним определение стохастического интеграла Ито от
случайного процесса X(t) по винеровскому процессу W(t):
\ x { t) d W { t) = l.i.m .£ 1* (f/) ( r ( f i+1) _ W{U)).
а
*=0
Определим обобщенный стохастический 0-интеграл следующим
образом:
1
X(t) dW(t) = l . i . m + 0 • (ti+l - ti))(W(ti+1) - Щ /,)),
a
1=0
р'
п—
где 0 < в < 1. При 0 = 0 имеем стохастический интеграл Ито.
При 0 = 1/2 получаемый интеграл называется стохастическим
интегралом Стратоновича. Пусть в качестве X(t) выступает
винеровский процесс W{t), так что рассматриваемый стохастический 0-интеграл имеет вид
т
W(t)dW(t).
/(0 ) = J
о
Вычислить значение /(0) при: 0 = 0; 0 = 1; 0 = 1/2.
Р е ш е н и е . Пусть сначала 0 = 0. Тогда
/(0 ) = l.i.m .£
W(ti)(W(tw ) - Щи)).
г=0
Обозначим &Wi = W{ti+\) — W{ti) и воспользуемся тождеством
W(ti)AWi = \ [ W 2 {ti+1) - W 2m
-
из которого имеем
W(U)AWi = \ [ W 2 {T) - r 2(0)] - i £ W i ) 2.
i=0
i= 0
n- 1
Ранее показывалось (см. задачу 5 к § 14), что l.i.m. ]Г(ДЦГ;)2 = Т.
Поэтому при Щ 0 ) = 0 получаем
m
1=0
= -l w 2 { T ) - l- T .
Заметим, что этот результат уже был получен в основном тексте
параграфа, хотя и несколько более громоздким путем.
Пусть теперь 0 = 1. Тогда
П—1
J(\) = U . m . ' £ W ( t i+l)AWi.
1=0
Но
W(ti+l) A W i = ( W(ti) + Д Wi)AWi = W ( td A W i + (Д W t ) 2 =
= \ [ W 2{tiH) - W 2{ti)] + \ { A W i)2,
так что
W(ti+l)AWi = ^ [ Г 2(Г) - r 2(0)] + 1
/=0
Отсюда следует, что
/=0
J { \ ) = y- W 2{ T ) + -l T .
Пусть, наконец, в — 1/2. Тогда
/ ( ± ) = l.i.m. £ Т О ) Д !^ ,
v /
1=0
где ft- = ^(ti + tj+1). Преобразуем выражение под знаком суммы:
W(7i) AWi = ( w(ti) + W(ti) - W(ti))AWi =
= W(ti)AWi + ( T O ) - W(td)AWi =
= W(ti)AWi + ( T O ) - W(ti))(W(ti+1) - T O ) + T O ) - T O ) ) =
= t o o д т о ( т о ь т о о ) 2+ ( т е ) - т о ж т о т ) - И * о ).
Поэтому
+ l.i.m. £ ( T O ) - T O O X T O + l) - Ш ) ) .
1= 0
При рассмотрении случая 0 = 0 было показано, что
l.i.m. ] Г Т О ) AWi = \ W { T ) - l- T .
i= 0
Рассуждая так же, как при решении задачи 5 к § 14, найдем
U . m . J 2 ( W ( t i) - W(ti ) ) 2 =
- U) = i T.
Наконец, пользуясь свойствами винеровского процесса, нетрудно
проверить, что
л—1
u .m . ^ 2 ( w ( t d - w m m u + i ) - w m
1=0
В результате получаем
= o.
Отметим, что в случае 0 = 1/2 для обобщенного стохастического 0-интеграла
т
J( 0 ) = W(t)dW(t)
о
получился такой же результат, как если бы в качестве W(t)
выступал не случайный процесс, а гладкая детерминированная
функция, и интеграл понимался в обычном римановском смысле.
5.
При измерении некоторой физической величины V показания v(t) прибора непрерывно автоматически записываются в течение времени Т. Величина
т
о
принимается за искомое значение измеряемой физической величины. Найти дисперсию D V j случайной величины Vj, если v(t)
рассматривается как реализация случайного процесса V(t) с корреляционной функцией
К у (т) = Ве~аМ,
В > 0,
Р е ш е н и е . Введем случайный процесс
т
о
а > 0.
где интеграл понимается в смысле среднеквадратичной сходимости. Он существует в силу вида корреляционной функции процесса V(t). Если через Kx(s, t) обозначить корреляционную функцию
процесса X(t), то
D VT = D{X(T)} = КХ(Т 9 Т).
Имеем:
тт
тт
Ве -<*1<2~й1 dtx d h
Кх(Т, Т) = ± 1 1 K v (th h) dh d h = ±
оо
00
Т J 2
_1_
Г
f(j Be~ad -h) dtx + [ Be~a{tl- t2)dt ij d h
Т2 J
2
о о
t2
.
т ц
т т
Т2 J
О о
г
= -L [ * (1 Г
В
А
J a
dh +
i f
-(1 - e~aT ■еы>) d h =
, OL
Т+ У * * ~ '>) +W a ( Т ~
- Ц) -
Отметим, что D V j —> 0 при Т —> оо, т. е. чем дольше длится наблюдение, тем точнее измеряем искомую величину.
6.
Известна корреляционная функция Кх(т) процесса X(t).
Определить дисперсию процесса
t
Y(t) = ^X{u)du,
являющегося интегралом в среднеквадратичном от X(t).
Р е ш е н и е . Согласно общему результату (см. основной текст)
искомая дисперсия может быть найдена по формуле
t t
Dy(t) =
| JKx(t\, t%) dt\
oo
В нашем случае
t t
t
Dy(t) =
t
—h ) d t \ d t 2 =
^ Kx(t 2 - t\)dt^jdt\ =
oo
oo
{заменяем переменные во внутреннем интеграле: т — t2 —t\, dt 2 = dr}
t
t-ti
= | ( J Kx {r) d r ) dti = | | K( t) dr dti,
o
-h
d
где последний интеграл берется по области, заштрихованной
на рис. 14 и представляющей собой параллелограмм.
К
D
-t
Рис. 14
Последний двойной интеграл можно представить в виде суммы двух повторных следующим образом:
t
0
t- т
t
JK{T)drdt\ = J Kx(r)dtijdT+ J^JKx{r)dt^dT,
o o
- t
-T
где первое слагаемое в правой части есть интеграл по верхнему
тругольнику, а второе — по нижнему треугольнику, из которых
состоит область D. Для первого слагаемого имеем
d
t
t —T
t
J(J Kx(T)dtijdT = jKx(T)(t-T)dT\
o o
о
для второго:
о
t
j(j
-t
—T
о
Kx{T)dt^j dr =
| Kx(r)(t + t ) dr.
—t
Если теперь в последнем интеграле произвести замену переменных
z — —ту
d z = —d r у
то получим
о
о
■K x ( r ) ( t + r ) d r = \ K x (—z ) ( t - z ) { - d z ) =
-t
t
t
= | K x { - Z ) { t - z) d z = J K x (z) ( t - z) dz,
о
о
где последнее равенство имеет место в силу четности функции Кх (т).
Таким образом, окончательно
t
D Y{t) = 2 \ { t - T ) K x { r ) dT.
О
7. Определить математическое ожидание M X 2 (t)f где
t
X { t ) = \ r 2 dK{T),
О
К(т) — пуассоновский случайный процесс интенсивности Л, а интеграл понимается в следующем смысле:
*
т.22 dK{T) =
О
l.i.m.
V-/2r
Y , ti [K{ti) - K { t ^ i)].
m a x A t i —>0 — '
i
i= 1
Р е ш е н и е . Воспользуемся известным тождеством
M X 2 (t) = DX(t) + (MX{t))2.
Для математического ожидания MX(t) имеем
Займемся теперь вычислением дисперсии DX(t):
DX{t) = M(X(t ) ) 2 = м (
l.i.m.
V tf [k(U) - K{ti-i)] x
i
1=1
I m ax
x
l.im
j
1
A ti—>0
f 2 t j [ k ( t j ) - k ( t M )]} =
J
j= 1
m a x A t j —►():— : 1
=
lim
m a x A t ;—>0 1 :
i
t= l
Последнее равенство здесь имеет место в силу свойства перестановочности операций вычисления математического ожидания
и предельного перехода и свойства независимости приращений
о
о
о
о
K(ti) — K (ti - 1) и K(tj) - K(tj_i) при i Ф j. Заметив, что
M (k(ti)-k(ti^
получим
lim
= D (k(ti)-fati-i)) = D ( K ( t i ) - m - i ) ) = \AU,
tjM(k(ti) - k ( t i - 1))2 =
т а х Д ^ — >0 .
i
))2
.
t
<=i
=
tjXAti = X \ Ч т = 1~ \ £ .
lim
m a x A / j - >0 .
1
t= l
i
„
0
5
Таким образом, окончательно
M X 2 (t) =
+ (^A /3) 2 =
+ ^A ¥ .
8.
Случайный процесс X(t) называется эргодичным no математическому ожиданию, если MX(t) = тх — постоянная величина и
т
1Ллп. j * ( 0 dt = mx ,
(6)
о
или, более развернуто,
J
Urn м ( к J X(t) dt - т х У = 0,
^
о
где интеграл понимается в смысле среднеквадратичной сходимости. Процесс вычисления предела в левой части (6) можно интерпретировать как процесс осреднения по времени, и в этом смысле
условие эргодичности (6) можно интерпретировать как равенство
среднего по времени среднему по ансамблю.
Пусть K(t) — пуассоновский процесс с интенсивностью А.
Определим процесс X(t) следующим образом:
а д = ™
Будет ли процесс X( t) эргодичным по математическому ожиданию?
Р е ш е н и е . Найдем математическое ожидание:
MX(t) = A f { ^ } = -MK(t)
=
т. e. математическое ожидание постоянно и можно проверять на
эргодичность. Имеем
Т
Т
М{ 1
т
-* (№
) ' - Ч т !о
о
= - > (
T
l.i.m.
V ^ A fc -
\ m a x A ^ —•() — ^
-
2 ^м
^
l.i.m.
г2йл»+л>-
V ^ A f ;
m a x A fy —>0^—
tj
( 1.Ш . E ® A ( ) + A ' =
y m a x A ^ O ^ ti
)
i
= _TLmaxA/i—
lim
/j/y
4
KAf,—>U
/
2Л
..
^ М К { и ) Ал
ло
lim > — l i i Д/,- + A2 =
7^ maxA^—>0 .
i
г
m ax A tj- ^ Q
1
v —v Am in(^, £,) -f- A2^ ; A
a
^
= -2
lim
-------—7~"—----^ A t i A t j T ma,xAti-+Q~?
t[tj
l>]
m ax A t ; - ^ 0
i
2A
——
/
A^
lim
> —“
—-A/,- + A2 =
^0 ^ titi
m a•
xfA/-—
A ^ —>0
i
i
T T
-*Jf(
00
T
Amin(7i,^2)
\ 2\ л
.
2A
+ A2^ dt\dt 2 —
J A dt + A2 =
fife
о
j j
T T
_1_
T2
Amin(fbfe) , ,
—
dt\dt 2 =
{см. рис. 15}
_1_
^ dt'd h + h \ \ u i dt'd h=
Г2
Аг
Г *i
DI
Т
h
( | А л . Ц + _L
О О
О О
Поскольку последнее выражение стремится к нулю при Т —>оо,
то процесс X(t) будет эргодичным по математическому ожиданию.
При проверке процесса на эргодичность по математическому
ожиданию часто оказывается полезным следующее утверждение,
справедливость которого несложно выводится непосредственно
из определения эргодичности.
Теорема. Необходимым и достаточным условием эргодичности случайного процесса X(t) с MX(t) = const по математическому ожиданию является выполнение равенства
ТТ
Ит
~2
jJK x i h J i ) dti di 2 = О,
оо
где Kx(t\,t 2 ) — корреляционная функция процесса X{t).
В частности, применительно к рассмотренному процессу
m
получим:
KX( h , t 2 ) = M { m ) m ) } = t V M { m ) k t 2)> - л min(fi, ^2)
t\t2
t\t2
j j
Y?
j]
T T
;2)^1
А"™ « , . Ы Л 1 Л г _ 2 Л
- ^2
00
0 0
что стремится к нулю при Т —> оо. Таким образом, использование
теоремы позволило получить нужный результат быстрее.
9.
Случайный процесс Х (0 называется эргодичным по дисперсии, если DX(t) — Dx — постоянная величина и
т
1 . ш 1 [ А о ) 2л = % ,
Т —+оо 1 J
0
или, более развернуто,
2
т
Н т Л* ( i
Dx ) = 0,
-
о
где интеграл понимается в смысле среднеквадратичной сходимости.
Определим случайный процесс X ( t) следующим образом:
W(t)
X(t) =
Vi
’
где W{t) — винеровский процесс, выходящий из нуля. Будет ли
процесс X(t) эргодичным по дисперсии?
Р е ш е н и е . Поскольку процесс X(t) — центрированный, то
дисперсия
г2 /
DX(t) = M X 2 (t) =
- Щ 0 )} 2 = y t = l
— постоянная величина и процесс 0 можно проверять на эргодичность по дисперсии. Эргодичность по дисперсии означает в данном
случае, что
т
11.1.т
• . —
1
Т—ю о Т
или, более развернуто,
t
Имеем
т
W2(t)
/1
W у 1' Л
1V
\
dt- 1
= МЛЛ 1
t
/
VТ
1 лл(
, •
w
~ T2
т
.1
(U) л „
L im
i
О
JV/2
,.
w
‘ ' ,„„:д"_0 ^
( h) л , \
((
V
V ^ A I , ) t l =
t;
1
ti
i
72 U \ w/2
т я у A t :—vO
V
VmaxA^—
>0“* ^^
lim
Е " < ^ 0 . ) П ) ) Д||,Д,
шах
T m
axA ^O —'
i
i,j
max A/1/—
>0
/
r max4m
T
A^—»0
= ±
w 2U d t Y - M ( l
t
J
\т
О
2и \
t,
Ы
T/
т
44
Utj
tiT -^ A fi + l =
lim
T m axA ^O ^
i
i,j
max Atj^O
j
—
tit/
lim
V Д^- + 1 =
T maxA/j-^0 .
/
г
= J,
,im
r
i
e
T maxA^ - U t j
4
max Afy—>0
i
.4 ,
ит
E f
T тахА ^О ^1
i
4
max Atj-^0
i
4 ,,4 ( r b
T
f
r2 u } y/ 2 (
l e i
t[tj
tl
M A ()_ N
Вычислим Af{lF2(^)tt^2(fy)}, считая пока, для определенности,
tj > ti'.
M { W 2 (ti)W 2 (tj)} = M { W 2 {ti)(W{tj) - W{ti) + W4*«))2} =
= М {^2( ^ - [ ( ^ ) - Щ ^ ) 2+ 2 (Щ ^ )-№ ))-Щ ^ )+ ^ 2иг)]} =
= M{ W2(ti) ■m t j ) - W(ti))2} + 2M{(W(tj) - W(ti )) • wHt i ) } +
+M
{ti) = ti • (tj —ti) + 0 + 3tf = 2 tf + t(tj,
а при произвольном соотношении моментов ti и tj получим
М { W 2 (ti)W 2 {tj)} = 2(min(fc, tj ) ) 2 + Щ.
Продолжая теперь основную цепочку равенств, найдем:
lim
•
-•
^ •
Т2
у Л1—/^
Т т
шп
ахяA1
►
0П^
i
’•
=
Щ
Ц
1
m ax A t j - + Q
1
/ 2(min(/t, /у))2
+ 1 j Ati Atj — 1 —
= ~2
lim
Е
Т m ax A ti —>>0 —^ V
Щ
1 .
~
m ax A t j —+0
••
тт
T T
/ ^ < :b fe g + i W
\
t\t2
' J
t\h
1
, 2_ i = д .
Z
Г2 J J
0 0
dt\ dt 2 .
^1^2
0 0
При вычислении последнего интеграла применим рис. 15:
тт
Г2
2(min(^i, £2))2I
t\t 2
I f f 9/2
JJ
оо
1 Г Г 9^2
А
2/2
-j^dh dti + -^2
Г2
2
Г2
d
A
D2
r f2
t
Ш
о 0
flf/l )rf/2 + -^2
2
dt\ dt 2
tx
(j }dtl=
о 0
_2_ ' 1 ^
Г2 Тч ~2
, 2 Г1
Г2JГ
f?
~2
~
Чтобы рассматриваемый процесс был эргодичным по дисперсии,
полученное выражение должно стремиться к нулю при Т —* оо.
Поскольку это не так, то процесс не эргодичен по дисперсии.
Заметим, что эргодичность процесса X(t) по дисперсии эквивалентна эргодичности процесса (X(t ) ) 2 по математическому ожиданию. Поэтому, чтобы исследовать эргодичность процесса X(t)
по дисперсии, можно найти корреляционную функцию K y( t\ ,t 2 )
процесса
а затем, опираясь на теорему, сформулированную при решении
задачи 8, проверить выполнение условия
1
ТТ
lim
гт.9
Т —+оо Т .
J/Су(^i, t2) dt\ dt 2 = 0.
00
Если это условие выполняется, то процесс X(t) будет эргодичным
по дисперсии; если не выполняется, то не будет.
V/Л — —
^ (0 то V/Л
В частности, если X(t)
Y(t) = — -— и
Vt
*
K Y{tu t2 ) = M { { Y { h ) - M Y { t x)){Y{t 2 ) - M Y { t 2))} =
t\
=
J\
_
w
t2
2m
_ w
+ 1
= } - , = A - M { w 4 t,) w 4 h ) } - 1=
= 7V (2 (m m « 1,(2))2 + M 2 ) - l = 2<mi'l(' b ' !))!
tit 2 v '
v
1
nt 2
так что
тт
тт
f2(ml
= l
hh
•5
00
00
rp
W(t)
— не стремится к нулю при Т —►оо, а значит, процесс —
не
vt
является эргодичным по дисперсии.
10.
Случайный процесс X(t) может принимать только два значения: 1 и —1. При этом
Р {Х (0 ) = 1} = Р { * ( 0 ) = - 1 } -
i
Переключение с одного значения на другое происходит в случайный момент времени Т, причем случайные величины Т и 1 (0 )
независимы. Случайная величина Т имеет показательное распределение с параметром А. Требуется найти корреляционную функцию Kx{t\,t2) процесса X(t) и выяснить, будет ли процесс X(t)
эргодичным по математическому ожиданию.
Р е ш е н и е . Найдем математическое ожидание MX{t). Имеем
по определению:
MX{t) = 1 • P{X(t) = 1} + (-1 ) • P{X(t) = -1}.
Для вычисления вероятностей используем формулу полной вероятности:
P{X(t) = 1} = P{X(t) = 1 1* (0 ) = 1} • Р {*(0) = 1} +
+ P{X(t) = 1 1* (0 ) = -1 } • О Д 0 ) = -1 } .
Ho
P{X(t) = 1 j J£T(0) = -1 } = P { T < t } =
1-
e~xt,
P{X(t) = 1 1X(0) = 1} = P { T > t } = e~xt.
Поэтому
p{X{t) = 1} = e - A< • i + (l - e - xt) ■i = i
Аналогично
P{X(t) = -1 } = 1,
так что в результате будем иметь
MX(t) = 0.
В таком случае для корреляционной функции получим
Kx { h , t 2 ) = M { X { t x)X{t2)} =
= P { X ( h ) X ( t2) = 1} - P { X ( h ) X ( t2) = -1 } .
Пусть сначала t2 > t\. Тогда
P { X ( h ) X ( t 2) - 1} = Р { Т i [tu h ]} = 1 - P { T € [tu t2]} =
h
= 1 - J Ae~xtdt = 1 +
e ~ Xh - e
~ xtl;
h
при этом
P { X ( h ) X ( t 2) = -1 } = 1 - P { X (h ) X ( t2) = 1} = e - A/‘ Таким образом, при t 2 > t\
Kxi h, t2) = 1 + e ~ xt2 - e~xt1 - (e~xt1 - e~xt2) = 1 а при t \ > t 2
Kx (tu t2) = \ - 2 e
~ xt2
+ 2e- xt>.
2 e~xtl
+ 2 e~xt2,
Чтобы ответить на вопрос об эргодичности процесса X(t) по
математическому ожиданию, исследуем поведение выражения
ТТ
~21
dt\ dt2
оо
при Т
сю. Понимая под областями D\ и D<i треугольники, показанные на рис. 15, имеем
тт
~~2 1 Ы ъ h) dt\ dt 2 —
0 0
^ ~ 2 e~xt{ + 2 e~xt2) dt\ dt 2 +
D\
+^ JJ(1- 2e“A
<2+2 e~xtl) d h dt 2 =
d
2
r/r2
^ (1 T2 J
0 0
2 e~xtl
\
+ 2 e~xt2) d h ) d t 2 +
т h
+ ^2
J(J(i - 2e~xt2 + 2 e~xt')dt 2) d t h
о 0
Вычисляя эти простые повторные интегралы, получим в итоге
_1_
Г2
тт
K x ( h , t2) dt\ dt 2 = \ + ^ ^ 2 0 ~ e XT) ~
+ e XT)-
оо
Поскольку это выражение не стремится к нулю при Т —>оо, то процесс X(t ) не является эргодичным по математическому ожиданию.
( l f t n - U -Ь И
I'
*ъ?»
СЕМАКОВ Сергей Львович
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И СЛУЧАЙНЫХ ПРОЦЕССОВ
Редактор B.C. Аролович
Оригинал-макет: А .А . П ярнпуу
Оформление переплета: В.Ф. Киселёв
П одписано в печать 23.08.11. Ф ормат 6 0 x 9 0 /1 6 . Бум ага оф сетная.
П ечать оф сетная. Уел. печ. л. 14,5. Уч.-изд. л. 14,6. Т ираж 500 экз.
З а к а з № К-6591.
И зд ател ьск ая фирма «Ф изико-м атем атическая литература»
М А Й К «Н аука/И нтерпериодика»
117997, М осква, ул. Проф сою зная, 90
E-m ail: fizm at@ m a ik .ru , fm lsale@ m aik .ru ;
h ttp ://w w w .fm l.ru
О тпечатано с электронны х носителей издательства
в ГУП «И П К «Чуваш ия», 428019
г. Ч ебоксары, пр-т И .Я ковлева, 13
ISBN 978-5-9221-1345-8
9785922113458
9 765922 113456