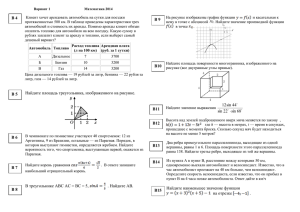
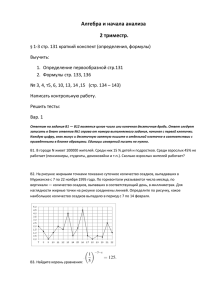
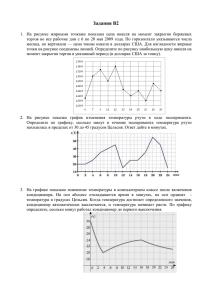
1. Одной банки краски хватает для покраски полосы от потолка до пола шириной 2 м. Какое наименьшее количество банок краски придётся купить для покраски чулана размерами 3 м на 2,5 м? 2. На рисунке жирными точками показано количество дневных осадков, выпавших в Новосибирске в период с 9 по 22 апреля. По горизонтали указывается день месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков за указанный период. 3. Сумма диагоналей квадрата равна 4. Найдите его площадь. 4. В небе кружат 4 голубя, 7 ворон, 3 воробья и 6 синиц. Игорь начинает считать птиц в произвольном порядке. Какова вероятность того, что первая птица, с которой он начнет счет, окажется ворона или синица? 5. Найдите корень уравнения (3x+2)^3=−64. Если уравнение имеет более одного корня, в ответе запишите больший из них. 6. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120∘. Найдите диаметр описанной окружности этого треугольника. 7. На рисунке изображен график функции y=f(x), определенной на интервале (−0,5;4,3). Определите количество целых точек (у которых координата – целое число), в которых производная функции отрицательна. 8. В правильной четырехугольной призме ABCDA1B1C1D1 известно, что DB1=2CD. Найдите угол между диагоналями AC1 и B1D. Ответ дайте в градусах. 9. Найдите значение выражения f(2x+3)−f(2x−7)−4, если f(x)=3x+14. 10. Совершенный газ описывается законом Менделеева-Клапейрона: pV=νRT, где p – давление в паскалях, V – объем в м3, ν – количество вещества в молях, T – температура в кельвинах, R – универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). В какое минимальное число раз надо увеличить температуру совершенного газа, чтобы при неизменном давлении его объем вырос не менее, чем в 5 раз?